一類特殊的Volterra型積分方程的解的存在性
葉陸紅, 楊海洋
(安慶師范學院 數學與計算科學學院,安徽 安慶 246133)
?
一類特殊的Volterra型積分方程的解的存在性
葉陸紅, 楊海洋
(安慶師范學院 數學與計算科學學院,安徽 安慶 246133)
摘要:本文主要應用壓縮映像原理討論了一類特殊的Volterra型積分方程的解的存在性問題,獲得解的存在性條件,并舉例說明了其應用。
關鍵詞:積分方程;解;不動點;映射
積分方程是含有對未知函數的積分運算的方程,數學、自然科學和工程技術領域中的許多問題都可以歸結為積分方程問題。積分方程理論的發(fā)展,始終與數學物理問題的研究緊密相連,它在工程、力學等方面有著極其廣泛的應用。
“積分方程”一詞是雷蒙德于1888年首先提出的。19世紀的最后兩年,瑞典數學家弗雷德霍姆和意大利數學家V.沃爾泰拉開創(chuàng)了研究線性積分方程理論的先河。從此,積分方程理論逐漸發(fā)展成為數學的一個分支。 1899年,弗雷德霍姆在給他的老師米塔-列夫勒的信中,提出如下的方程
1900年,弗雷德霍姆在其論文中把上方程稱為“積分方程”,形如
和
的積分方程,依次稱為第一種沃爾泰拉積分方程和第二種沃爾泰拉積分方程。它與弗雷德霍姆積分方程的不同之處,僅在于它的積分上限是變量x,且σ≤y≤x≤b,此處σ,b是常量。沃爾泰拉積分方程可視為弗雷德霍姆積分方程的核K(x,y)當y>x時為零的情形。最早被研究的一個帶弱奇性核的沃爾泰拉積分方程,是阿貝爾方程,它是N.H.阿貝爾于1823年在求一個質點的落體運動軌跡與時間的關系中得到的。
隨著計算技術的發(fā)展,作為工程計算的重要基礎之一,積分方程進一步得到了廣泛而有效地應用。如今物理問題變得越來越復雜,積分方程變得越來越有用。 它的形成和發(fā)展是很多重要數學思想和概念的最初來源和模型。例如,對泛函分析中平方可積函數、平均收斂、算子等的形成,對一般線性算子理論的創(chuàng)立,以至于對整個泛函分析的形成都起著重要的推動作用。
解的存在性理論是常微分方程最基本和最重要的理論之一,它一般通過構造逐步逼近函數序列來說明其解的存在性。本文主要應用壓縮映像原理來討論積分方程
(1)
的解的存在性問題,其中f(x)在[a,b]上連續(xù),K(x,ξ)是a≤x≤b,a≤ξ≤b上的連續(xù)函數,λ為常數。
定義1[1]設R是按距離ρ的度量空間,A是R到自身的一個映照,若存在α∈[0,1)使對一切x,y∈R有ρ(Ax,Ay)≤αρ(x,y),則稱A是R上的一個壓縮映照。
定義2[1]設A是R到自身的一個映照,若x∈R使Ax=x,則x是A的一個不動點。
引理1[1]在完備的度量空間中的壓縮映照必有唯一的不動點。
引理2[1]設度量空間R完備,B是R到R的映照,若存在一個自然數n,使Bn是R上的一個壓縮映照,則B在R中必有唯一的不動點。
定理設f(x)在[a,b]上連續(xù),K(x,ξ)是a≤x≤b,a≤ξ≤b上的連續(xù)函數,若|λ|足夠小,則方程(1)存在唯一的連續(xù)解。
證明構造C[a,b]到C[a,b]映射:
B∶φ∈C[a,b]→Bφ∈C[a,b]
其中f(x)在[a,b]上連續(xù),K(x,ξ)是a≤x≤b,a≤ξ≤b上的連續(xù),故有界,即存在正的常數M使|K(x,ξ)|≤M。
?φ1(x),φ2(x)∈C[a,b],當x∈[a,b],有:
|Bφ1(x)-Bφ2(x)|=
|λ|M(b-a)‖φ1-φ2‖
下面利用歸納法證明:當x∈[a,b]時,有

當n=1顯然成立。設上式對n成立,下面證明對于n+1也成立。
事實上,
|Bn+1φ1(x)-Bn+1φ2(x)|=
取自然數n使:

則

α‖φ1-φ2‖
由引理知,方程(1)在C[a,b]中必有唯一解。
注方程(1)解的存在性還可以通過構造逐步逼近函數序列
來證明。
下面舉例說明以上定理的應用。
例討論積分方程
(2)
的解的存在性,其中y(t)∈C[0,1],λ為常數,|λ|<1。
分析此方程等價于:
z(t)=e-tx(t),ξ(t)=e-ty(t)
令
則
即T是壓縮映射,壓縮常數|λ|<1,因而T有唯一的不動點,即積分方程
在C[0,1]上有唯一的不動點,因此原方程在C[0,1]上有唯一解。
下面介紹用逐步逼近法求解方程的過程。
定義C[0,1]上映射:
取k(t,s)=et-s,φ0=0,φn=Knφ0,則有
φ1(t)=y(t)
一般地有
所以,kn(t,s)由遞推關系確定:
k1(t,s)=k(t,s),
函數列{φn(t)}是[0,1]上的連續(xù)函數,并且在[0,1]上均勻收斂于φ*(t),故對給定正數ε只要取n使

有
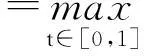
即積分方程的第n次逼近解φn的誤差小于ε。
參考文獻:
[1] 夏道行.實變函數與泛函分析[M].北京:高等教育出版社,2010:68-77.
[2] 張恭慶.泛函分析講義[M]. 北京:北京大學出版社,2003: 10 .
[3] 東北師大數學系.常微分方程[M]. 北京:高等教育出版社,2005:78-90.
[4] 王高雄.常微分方程[M]. 北京:高等教育出版社,2006:75-89.
[5] 張海,舒阿秀.Banach不動點定理的注記及應用[J].安慶師范學院學報(自然科學版),2005,16(4):97-100 .
Existence of Solutions for a Class of Special Volterra Integral Equations
YE Lu-hong, YANG Hai-yang
(School of Mathematics and Compution Science, Anqing Teachers College, Anqing 246133, China)
Abstract:By means of contraction mapping principle, we discuss the existence of solutions for a class of special Volterra integral equations, and obtain the existence conditions of solutions, and give an example to illustrate its application.
Key words:integral equations, solutions, fixed point, mapping
文章編號:1007-4260(2015)02-0007-03
中圖分類號:O175
文獻標識碼:A
作者簡介:葉陸紅,女,安徽潛山人,碩士,安慶師范學院數學與計算科學學院講師,研究方向為微分方程理論及其應用。
基金項目:安慶師范學院青年科研 (KJ201107),安徽省高等學校省級教學研究項目(2012jyxm364)和安徽省高校自然科學研究一般項目(AQKJ2014B010)。
收稿日期:2014-08-28

