基于灰色關聯分析的“白屋頂計劃”評價模型

黃 果 成

(安徽師范大學 數學計算機科學學院，安徽 蕪湖 241003)

?

基于灰色關聯分析的“白屋頂計劃”評價模型

黃 果 成

(安徽師范大學 數學計算機科學學院，安徽 蕪湖 241003)

摘要：在已知人為熱釋放、風速、日照時數和相對濕度的前提下，以蕪湖市為例，運用灰色關聯分析求出以上四個影響因素對行為因子(城市熱島效應)的關聯影響程度，算出日照時數在四個環境因子中的比重，從而將白色屋頂計劃對城市熱島效應的作用量化，建立了灰色預測模型。通過回歸分析計算白屋頂計劃對城市溫度的影響，最后將預測數據與真實數據進行對比，模型結果表明“白屋頂計劃”是合理且可行的。

關鍵詞：灰色預測；熱島效應；關聯程度；量化對比

熱島效應，指由于人為原因，改變了城市地表的局部溫度、濕度、空氣對流等因素，進而引起的城市小氣候變化現象。該現象，屬于城市氣候最明顯的特征之一。由于城市化的速度加快，城市建筑群密集、柏油路和水泥路面比郊區的土壤、植被具有更大的吸熱率和更小的比熱容，使得城市地區升溫較快，并向四周和大氣中大量輻射，造成了同一時間城區氣溫普遍高于周圍的郊區氣溫，高溫的城區處于低溫的郊區包圍之中。開展城市熱效應的研究，對于了解人類活動影響城市氣候的規律，降低城市環境污染，控制能耗，增進城市居民的健康水平等都具有重要的意義。而“白屋頂計劃”正是解決熱島效應這一頑疾的方法之一。“白屋頂計劃” 是由美國一些環保志愿者提出而被政府所采納的政策。他們號召人們將屋頂漆成白色，以增加建筑物對陽光的反射，降低室內溫度。而這么做的好處是：節約能源，遏制全球變暖；減小城市熱島效應和霧氣；提高室內居住者的舒適度；符合綠色建筑標準。

通過研究分析，影響城市熱島效應主要有人為熱釋放、風速、日照時數以及相對濕度等四個因素。而這四個因素對熱島效應的影響程度各不相同。因此，我們選取了內陸城市蕪湖作為研究對象，找出了人為熱釋放、風速、日照時數以及相對濕度影響城市熱島效應的因子在2008年—2013年的數據(表1)來對蕪湖城市熱島效應進行分析。由于熱島效應的衡量需要繁瑣的運算過程，所以我們通過蕪湖市全年的平均值來計算熱島效應。

1系統模型

1.1灰色關聯分析

灰色關聯分析法是根據數列的可比性、可近性分析系統內部主要因素之間的相關程度，定量地描述系統內部結構之間的聯系，是對系統內部各事物之間狀態的量化比較分析。由于本文的行為因子只有一個，即城市熱島效應，因此，我們采用灰色關聯中的單因子分析。

1.1.1構造參考數列和比較數列

給定負理想方案環境因子指標集都成參考數列：

x0={x0(k)|k=1,2,3,4}=

(x0(1),x0(2),…x0(4))

該參考數列中的元素是四個環境影響因子對城市熱島效應影響預測值中的最劣值，以此來表示負理想方案的環境因子的評價指標集：

表1　2008年到2013年安徽蕪湖市四項環境因素的統計數據

表示負理想方案的指標集，X′(k)為相應的環境因子的最劣預測值。

設系統的行為因子x0的參考數列為

x0={x0(k)|k=1,2,3,4}=

(x0(1),x0(2),x0(3),x0(4))

相關因素為xi(i=1,2,…,4),即比較數列

xi={xi(k)|k=1,2,…,4}=

(xi(1),xi(2),xi(3),xi(4)) (i=1,2,…,m)

則參考數列對于各比較數列間的絕對差為

Δi(k)=|x0(k)-xi(k)|

(i=1,2,…,4;1≤i≤m)

記Δi=(Δi(1),Δi(2),Δi(3),Δi(4)),稱之為差數列。

1.1.2同一化純量處理和灰色關聯系數的求解

對于越大越優的指標，用公式(1)進行同一化純量處理：

k=1,2,3,4

(1)

對于越小越優的指標，用公式(2)進行同一化純量處理：

k=1,2,3,4

(2)

該城市熱島效應的環境因子的評價指標集{X′(k)}按公式(1)(2)同一化純量處理后得到的生成比較數列{X(k)}，k=1,2,3,4。

同時，定義比較數列xi對參考數列x0在第k點的灰關聯系數為

r(x0(k),xi(k))=

其中常數α∈[0,1],稱為分辨率系數。顯然，當α越大時，分辨率越大；當α越小時，分辨率越小，一般情況下取α=0.5。

對于所有的點k=1,2,…,4,則定義比較數列xi對行為因子x0的關聯(影響)程度。得出各數列對行為因子x0的關聯(影響)程度，通過計算日照時數對行為因子x0的關聯度占整個因素對行為因子x0關聯度和的比重,就可以通過量化間接地評估白屋頂計劃對降低城市熱島效應所起的作用。

1.2灰色預測模型的建立

1.2.1數據的檢驗與處理

首先，為了保證建模方法的可行性，需要對已知數據列做必要的檢驗處理。設參考數據為x0=(x0(1),x0(2),…,x0(n))，計算數列的級比

1.2.2建立模型GM(1,1)

設已經參考數據列為x0=(x0(1),x0(2),…,x0(n))，做一次累加(AGO)生成數列

x(1)=(x(1)(1),x(1)(2),…,x(1)(n))=

(3)

(x(1)(1,)x(1)(1)+x(0)(2),…,x(1)(n-1)+x(0)(n))

(4)

Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)

(k=2,3,…,n)

則

Z(1)=(Z(1)(2),Z(1)(3),…,Z(1)(n))

于是建立的灰色微分方程為

x(0)(k)+aZ(1)(k)=b， (k=2,3,…,n)

對應的白化微分方程為

(5)

記u=(a,b)T，Y1=(x(0)(2),x(0)(3),…,x(0)(n))T,

(6)

于是求解方程(6)得預測值：

(k=1,2,…,5)

而且，

(7)

(k=1,2,…,5)

(8)

則u=(u1,u2,…,u12)，于是可得2013年每一個月的指標值為Y=X·u。

1.2.3檢驗預測值

通過前面的歷史數據求出2013年的指標值之后，我們對得到的指標值來進行檢驗，如果結果能達到要求，就可以說明我們建立的模型是合理的。這里我們用殘差檢驗法來檢驗預測值。

令殘差為

如果ε(k)<0.2,則可以認為達到一般要求；如果ε(k)<0.1,則認為達到較高的要求。

2灰色預測

2.1求解各影響因子的關聯度

表2　分別算出各影響因子在2008年—2013年的年平均數據

分別將表格中的原始數據采用標準化方法進行無量綱化處理。從而得到各因素對城市熱島效應影響的標準化矩陣，

人為熱釋放量：

Q1=[1 0.981 0.992 0.993 0.995 0.998]

在求風速對城市熱島效應的影響時，由于表格中給出的數據是一定范圍之間的數據，所以需要將其做前期處理，即取兩區間的平均值。

風速：

Q2=[1 1.061 1.066 1.069 1.008 1.065]

日照時數：

Q3=[1 1.030 1.034 1.033 0.992 1.001]

相對濕度：

Q4=[1 0.967 1.048 1.409 1.600 1.425]

所以，總的比較數列為

參考數列為

分別求兩組標準化數據序列中母序列與各子序列在各時刻的絕對差Δij(t),得到影響城市熱島效應的四個環境因子的數據序列的差值矩陣：

V(k)=

由該矩陣可知最大絕對差值Vmax為5.720，最小絕對差值Vmin為0.000。取α=0.5，代入式：

r(x0(k),xi(k))=

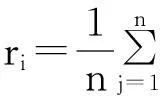
表3　四個環境因子的關聯度

因此，日照時數在四項環境因子中所占比重為

所以，相對于其他三個環境因子，日照時數對城市熱島效應所起到的作用為0.25，也就是白屋頂計劃對城市熱島效應所起到的作用為0.25。

2.2白屋頂計劃的熱量吸收

由上面的計算可知，白屋頂計劃可以吸收城市每天大約25%的熱量，因此可以使得城市熱島效應被大大降低。與此同時，我們要考慮吸收的熱量能最終降低多少溫度，能否被人體感知。我們可以通過建立回歸方程來得到溫度的降低值。采用一元線性回歸建立在實行了白屋頂計劃的情況下熱量被吸收與溫度下降的線性關系，運用Matlab統計工具箱中的回歸分析命令。設回歸方程為

Q=a+b*ΔT

由此得到全年不同月份城市熱量下降值Q。再將該熱量下降值帶入溫度計算公式中，可以得到全年平均氣溫將下降1到1.5攝氏度。根據氣象學資料分析可知，該種程度的降溫足以使人體感知，因而再次說明白屋頂計劃有效。

2.3通過灰色預測檢驗模型的合理性

由已知數據，對于2008年—2013年某項指標記為矩陣A=(aij)5×12，計算每年的年平均值，記為

x(0)=(x(0)(1),x(0)(2),…,x(0)(5))

(9)

對x(0)作一次累加，則

(i=2,3,4,5)

記

x(1)=(x(1)(1),x(1)(2),…,x(1)(5))

(10)

(1) 相對濕度

由表1中數據，用(9)，(10)式計算可得年平均值、一次累加值分別為

x(0)=(0.789 5,0.763 4,0.827 9,1.112 1,1.263 6)

x(1)=(0.789 5,1.552 9,2.380 8,3.492 9,4.756 5)

顯然x(0)的所有級比都在可容區域內。經檢驗，在這里取參數α=0.5比較合適。由

z(1)=(z(1)(2),z(1)(3),,z(1)(4),z(1)(5))

則有

z(1)=(1.253 1,1.752 1,2.831 8,4.151 7,5.457 2)

由最小二乘法求得

a=-0.099 3,b=85.598 5

由(8)式可得每月的比例為

u=(0.079 4, 0.080 7, 0.074 9, 0.078 6,

0.081 9, 0.081 8, 0.084 5, 0.083 8,

0.087 2, 0.088 6, 0.086 6, 0.092 0)

故2013年1—12月的預測值為

Y=u·X=(1.214 3, 1.215 7, 1.101 2,

0.977 5, 1.000 0, 0.994 1, 0.995 2,0.953 3,

1.213 6, 1.215 7, 1.273 5, 1.313 2)

將預計值與2013年實際統計值進行比較，見表5。

(2) 日照量

由表1中數據，用(9)，(10)式計算可得年平均值x(0)、一次累加值x(1)。取參數α=0.5，由

z(1)=(z(1)(2),z(1)(3),,z(1)(4),z(1)(5))

可求得加權平均值z(1)。由(6)-(8)式可求得

年總值X=1 843.08(h/年)以及

u=(0.040 7, 0.073 2, 0.070 3, 0.087 8,

0.090 7, 0.084 8, 0.083 6, 0.102 2,

0.101 0, 0.104 1, 0.091 4, 0.070 1)

于是可得2013年日照量的預測值，并與實際值比較，見表5。

(3) 風速

由表0中數據，用(9)，(10)式計算可得年平均值x(0)、一次累加值x(1)。取參數α=0.5，由

z(1)=(z(1)(2),z(1)(3),z(1)(4),z(1)(5))

可求得加權平均值z(1)。由(6)(7)(8)式可求得

年總值X=34.236(m/s)以及

u=(0.109 1, 0.067 9, 0.070 7, 0.090 2,

0.078 1, 0.084 1, 0.097 8, 0.091 1,

0.087 3, 0.089 9, 0.133 8, 0.075 1)

可以得2013年風速的預測值，并與實際值比較，見表5。

(4) 人為熱釋放

仍由表1中數據，用(9)，(10)式計算可得年平均值x(0)、一次累加值x(1)。取參數α=0.5，由

z(1)=(z(1)(2),z(1)(3),,z(1)(4),z(1)(5))

可求得加權平均值z(1)。由(6)(7)(8)式可求得

a=-0.087 3,b=78.125 2,=0.752(kJ),

年總值為X=9.024(KJ)以及

u=(0.089 3, 0.072 1, 0.066 9, 0.093 2,

0.083 1, 0.079 4, 0.107 8, 0.093 1,

0.065 3, 0.098 1, 0.101 8, 0.05 1)

表5　2013年人為熱釋放量的預測值與實際值的比較

由表5可以看出，預測值與實際值差別很小，可以視為預測準確，從而判斷上述四個因素正確。

2.4檢驗預測值

3結束語

本文利用灰色關聯分析的方法分析了“白色屋頂計劃”對于緩解城市熱島效應的作用，并通過實際數據與預測數據結合的方法建立了灰色預測模型，根據得到的數據對“白屋頂計劃”的合理性以及溫度下降的感知度的有效性方面進行了檢驗。實驗結果表明，“白屋頂計劃”具有重大的現實意義與可操作性。下一步研究就圍繞“白屋頂計劃”的實際運作方面來展開。

參考文獻:

[1] 韓中庚.《數學建模方法及其應用》[M].(第二版). 北京: 高等教育出版社,2005.

[2] 姜啟源.《數學模型》[M].(第三版). 北京: 高等教育出版社，2003.

[3] 鄧聚龍.《灰預測與灰決策》.[M]. 武漢: 華中科技大學出版社，2002.

[4] 陳志，王濤.《城市熱島效應的灰色評價與預測》[J].西安:西安交通大學學報，2004(9)：15-17.

[5] HUANG G B ,ZHU Q Y,SIEW C K. Extreme Leading Machine: Theory and Applications[J]. Neurocomputing, 2006(70):489-501.

[6] HUANG G B ,ZHU Q Y,SIEW C K. Extreme Leading Machine:a New learning Scheme of Feedford Neural Networks[C]. Proceedings of International Joint Conference on Neural Networks,25-29 July,2004,Budpaest Hungary.

[7] GUO R F,HUANG G B,LIN Q P,et al. Error Minimized Extreme Leading Machine with Growth of Hidden Nodes and Incremental Learning[J]. IEEE Transactions on Neural Networks,2009,20(8):1352-1357.

[8] ZHU Q Y,QIN A K,SUGANTHAN P N,et al. Evolutionary Enviromental Protection[J]. ParternRecognition,2009(38):1566-1576.

[9] 安徽省蕪湖市氣象局.蕪湖市氣象資料.[EB/OL]. http://218.22.3.218/product/qhmonitor.asp, 2014.2.20/2014.3.9.

Based on Grey Relational Analysis of “White Roof Plan” Feasibility Evaluation Model

HUANG Guo-cheng

(School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)

Abstract:In order to solve the urban heat island effect, Aiming at high efficiency, low cost and easier implementation, a grey relational analysis is proposed based on the “white roof plan”. In this paper, taking Wuhu city as an example, release, wind speed in the known anthropogenic heat, condition number and relative humidity of sunshine, we first use the grey correlation analysis to find the four factors (anthropogenic heat release rate, wind speed, solar radiation, relative humidity) on behavior factor (urban heat island effect) correlation degree of influence, and calculate the sunshine hours in four environmental factors in the proportion, which will be white roof plan to quantify the role of urban heat island effect, and then establish the gray forecast model. Finally, the prediction data and the real data experiments are compared. The simulation results show that the "white roof plan" is feasible and reasonable.

Key words:gray prediction, heat island effect, degree of correlation, quantitative comparison

文章編號：1007-4260(2015)02-0031-06

中圖分類號：TP393

文獻標識碼：A

作者簡介：黃果成，男，安徽安慶人，安徽師范大學數學計算機科學學院學生。

基金項目：教育部人文社科青年 (11YJC880119)。

收稿日期：2014-03-20