參數(shù)激勵非線性振動時滯反饋最優(yōu)化控制
第一作者劉燦昌男,副教授,1970年3月生
郵箱:sdutlcch@163.com
參數(shù)激勵非線性振動時滯反饋最優(yōu)化控制
劉燦昌,岳書常,許英姿,沈玉鳳,任傳波,劉露,荊棟
(山東理工大學(xué)交通與車輛工程學(xué)院,山東淄博255049)
摘要:研究含時滯的線性、非線性復(fù)合時滯反饋控制Duffing-Van der Pol振子主參數(shù)共振響應(yīng)最優(yōu)化控制參數(shù)確定。基于弱非線性、弱反饋控制、弱參數(shù)激勵及小阻尼假設(shè),據(jù)平均法獲得穩(wěn)態(tài)響應(yīng)振幅、相位平均方程。通過非線性振動能量比值定義衰減率。以衰減率為振動控制參數(shù)優(yōu)化目標(biāo),以非線性振動系統(tǒng)振動穩(wěn)定條件、幅值最值、最優(yōu)時滯為約束條件,利用最優(yōu)化方法計算獲得最佳線性、非線性反饋控制參數(shù)。
關(guān)鍵詞:非線性振動;控制;時滯;參數(shù)激勵
基金項目:國家自然科學(xué)面上基金(51275280)
收稿日期:2014-04-23修改稿收到日期:2014-09-12
中圖分類號:O322
文獻(xiàn)標(biāo)志碼:A
DOI:10.13465/j.cnki.jvs.2015.20.002
Abstract:The determination of optimal control parameters of resonant response was studied for a Duffing-Van der Pol oscillator with delayed linear and nonlinear feedback controllers. With the weak nonlinearity, weak feedback control, small damping, and soft excitation, the average equations for the amplitude and phase of the stable vibration were obtained. The regions of the feedback gains for stable vibration of the nonlinear vibration system were derived by using the stable conditions of the eigenvalue equation. The nonlinear vibration energy attenuation ratio was defined as the proportion of the squares of vibration peaks at primary resonance of the suspension system with and without control. Taking the energy attenuation ratio as an objective function, the stable conditions and the optimal delay as constraint conditions, the optimal feedback control gains can be worked out by using optimal method. It is found that an optimal feedback gain can lead to an optimal control performance.
Optimal control of parametric excitated nonlinear vibration system with delayed linear and nonlinear feedback controllers
LIUCan-chang,YUEShu-chang,XUYing-zi,SHENYu-feng,RENChuan-bo,LIULu,JINGDong(School of Transportation and Vehicle Engineering,Shandong University of Technology, Zibo 255049, China)
Key words:nonlinear vibration; control; time delay; parametric excitation
Duffing-Van der Pol振動系統(tǒng)為兩種典型非線性系統(tǒng)組合,大量存在于力學(xué)與工程、激光物理、化學(xué)、聲學(xué)及生命科學(xué)中,具有豐富、復(fù)雜的動力學(xué)行為。通過對該模型動力學(xué)行為控制,可提高結(jié)構(gòu)穩(wěn)定性及適應(yīng)性。
近幾年,該系統(tǒng)動力學(xué)行為分析與控制成為非線性控制領(lǐng)域重要研究課題[1-2]。甘春標(biāo)等[3]探討Van der Pol-Duffing振子在強共振下的分岔解、系統(tǒng)鎖頻周期分岔運動及擬周期分岔運動。陳予恕等[4]研究主參數(shù)共振下具有廣義Van der Pol阻尼及5次Duffing恢復(fù)力的參數(shù)激勵非線性系統(tǒng)二次近似分叉行為。黃志龍等[5]研究諧和激勵下強非線性Duffing-Van der Pol振子鎖相運動。褚衍東等[6]探討反饋控制參數(shù)對系統(tǒng)運動控制到穩(wěn)定的周期軌道影響,利用數(shù)值方法研究周期激勵下Van der Pol-Duffing振子混沌行為及控制。Maccari[7]利用漸近攝動法研究Duffing-Van der Pol振子主共振時產(chǎn)生倍周期運動的充分條件。Xu等[8]發(fā)現(xiàn)倍周期分岔及環(huán)面破損為由Duffing-Van der Pol振子主共振混沌運動出現(xiàn)的兩種途徑。
利用時滯反饋對非線性振動系統(tǒng)動力學(xué)行為進(jìn)行控制為非線性動力學(xué)理論的重要研究方向[9-15]。Tsuda等[16]研究含時滯的Duffing-Van der Pol振子主共振與1/2亞諧共振的混沌運動。李欣業(yè)等[17-18]研究時滯反饋控制下Duffing-Van der Pol振子主參數(shù)共振及主共振響應(yīng),討論反饋時滯、反饋增益對系統(tǒng)響應(yīng)影響及極限環(huán)振幅、穩(wěn)定性問題。楊平[19]以含時滯反饋的Van der Pol-Duffing系統(tǒng)為對象,研究時滯量、位移反饋增益變化對雙Hopf分岔影響,獲得共振雙Hopf分岔引起的各種周期解近似解析解及穩(wěn)定性條件。
Duffing-Van der Pol為多參數(shù)控制系統(tǒng),研究其動力學(xué)行為時需采用嘗試法選定反饋控制參數(shù),再討論控制參數(shù)變化其控制效果的變化,確定有效控制參數(shù)。實際上在合理的控制范圍內(nèi)會存在對系統(tǒng)動力學(xué)行為起作用的無窮多組參數(shù),但尋找到最優(yōu)控制參數(shù)非常困難。以上研究大多討論控制參數(shù)對非線性振動系統(tǒng)動力學(xué)行為影響,如分岔控制、混沌控制等,較少涉及最優(yōu)控制參數(shù)確定。而實際工程問題中對非線性振動系統(tǒng)的減振降噪也為控制目標(biāo),能量消耗最少、效果最佳為非線性振動控制的重要研究課題。
1平均方程
參數(shù)激勵下Duffing-Van der Pol振子非線性振動的減振控制研究已展開,該模型動力學(xué)方程非線性部分同時含Van der pol系統(tǒng)維持自激振動的非線性阻尼項及Duffing系統(tǒng)三次非線性恢復(fù)力項。以弱非線性、弱反饋控制、弱參數(shù)激勵及小阻尼為減振控制工況,Duffing-Van der Pol振動系統(tǒng)動力學(xué)方程[18]可寫為
(1)
式中:ω0為線性振動系統(tǒng)圓頻率;α為非線性項系數(shù);μ,ν分別為線性、非線性阻尼系數(shù);F為激勵幅值;gd,gv分別為線性反饋增益;ga1,ga2分別為非線性反饋增益;ε為正的小參數(shù)。
對振動系統(tǒng)主共振情形,引進(jìn)調(diào)諧參數(shù)σ,得
(2)
據(jù)平均法,為簡化計算,令Ω=2,式(1)的近似解為
u=acos(t-θ)
(3)
式中:a為振幅;θ為相位;二者隨時間慢變的,且控制方程[19-21]為
(4)
(5)
式中:f為式(1)所含ε項全部移到等號右邊時ε的系數(shù),即
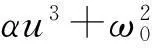
(6)
對式(4)、(5)積分,得
(7)
(8)
μe=μ-gdsinτ1+gvcosτ2
(9)
(10)
(11)
(12)
式(7)、(8)表明有零固定點、非零固定點兩類,分別對應(yīng)原系統(tǒng)零解、周期解。由于反饋增益及時滯的出現(xiàn),平均方程中各項系數(shù)均發(fā)生變化,因而可通過線性與非線性控制項及時滯聯(lián)合控制實現(xiàn)對非線性振動系統(tǒng)動力學(xué)控制。
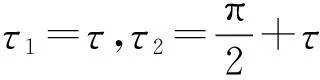
μe=μ-(gd+gv)sinτ
(13)
(14)
(15)
(16)
式(13)~式(16)為阻尼、調(diào)諧、非線性阻尼、非線性項參數(shù)與時滯及線性、非線性反饋參數(shù)的函數(shù)關(guān)系表達(dá)式。隨非線性線控制器的引入,非線性振動控制手段較豐富,控制參數(shù)可調(diào)范圍變大。
2主參數(shù)共振周期解的穩(wěn)定性
(17)
(18)
消掉式(17)、(18)中θ,得幅頻方程為
(19)
設(shè)定線性、非線性控制參數(shù)值及時滯,令σe+k2a2=0,非線性振動系統(tǒng)能量可表示為
(20)
為簡化分析,僅取含正號情況,式(20)寫為
(21)
作為對照,無控制時系統(tǒng)能量表示為
(22)
將控制系統(tǒng)能量與無控制系統(tǒng)能量比值定義為系統(tǒng)的衰減率,寫為
(23)
式(23)表示有、無控制的振動能量比值。衰減率與激勵幅值、線性、非線性阻尼系數(shù)、激勵頻率、控制參數(shù)與時滯有關(guān)。衰減率數(shù)值較小時非線性振動系統(tǒng)主共振減振效果較好,可通過選擇適當(dāng)反饋控制參數(shù)及時滯獲得數(shù)值較小衰減率。與線性反饋控制策略相比,非線性時滯反饋控制對非線性原振動系統(tǒng)非線性項也得到控制,增大參數(shù)的可調(diào)范圍。
3非零解的穩(wěn)定性
分析非零解的穩(wěn)定性。由式(7)、(8)可得非零解對應(yīng)的Jacobi矩陣特征值方程為
λ2+2m1λ+n1=0
(24)
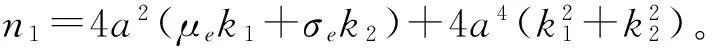
據(jù)Routh-Hurwitz準(zhǔn)則,非零解是漸近穩(wěn)定的,當(dāng)且
(25)
對式(25)第一式進(jìn)行縮小處理,得
μe≤0,k1<0
(26)
由式(25)第二式可得
(μek1+σek2)≥0
(27)
所得保持原系統(tǒng)非線性振動非零解為漸近穩(wěn)定的反饋控制參數(shù)取值范圍。
4主參數(shù)共振最優(yōu)化控制參數(shù)計算
通過對非線性振動系統(tǒng)穩(wěn)定性分析,獲得反饋控制參數(shù)取值范圍;通過求解非線性振動幅頻方程獲得振幅峰值,以此為約束條件,以衰減率為目標(biāo)函數(shù),利用最優(yōu)化原理確定最佳控制參數(shù)。為簡化分析,時滯取τ=(2kπ+π/2),(k=0,1,2,3,…),其它時滯計算方法類似。
(28)
s.t.μe≤0
(29)
k1≤0
(30)
μek1+σek2≥0
(31)
(32)
(33)
式中:η為衰減率控制范圍參數(shù)。
式 (29)~式(31)可保證系統(tǒng)的非零解為漸近穩(wěn)定的;式(32)為振動峰值的取值條件;式(33)為衰減率的約束條件。通過引進(jìn)調(diào)節(jié)參數(shù),可據(jù)具體工程要求設(shè)置衰減率數(shù)值,并求出與其相匹配的最優(yōu)化控制參數(shù)。用最優(yōu)化參數(shù)計算方法可解決非線性振動控制工程中最佳控制參數(shù)確定問題。
5仿真算例分析
以含時滯的非線性位移、速度反饋Duffing-Van der Pol振子主參數(shù)共振響應(yīng)為例進(jìn)行研究。其中非線性項系數(shù)α=1,線性、非線性阻尼系數(shù)μ,ν均取1.5,激勵幅值F=2.5。線性控制的反饋增益gd,gv均為1,時滯為2。復(fù)合控制的線性反饋增益gd,gv均為1,非線性反饋增益ga1,ga2及時滯均為2。
利用遺傳算法工具箱計算含約束的減振控制參數(shù)最優(yōu)化值,種群取50,交叉率0.8,最大進(jìn)化代數(shù)設(shè)為200,其它參數(shù)用默認(rèn)取值,計算獲得線性、非線性反饋控制增益參數(shù)。利用Matlab軟件數(shù)值模擬得1/2主參數(shù)共振下幅值-頻率關(guān)系曲線,無、有控制幅值-頻率關(guān)系曲線見圖1。由圖1(a)看出,無反饋控制時非零解存在多解現(xiàn)象,系統(tǒng)處于不穩(wěn)定狀態(tài)。圖1(b)為線性控制器控制的幅頻關(guān)系曲線,非零解存在多解現(xiàn)象,系統(tǒng)處于非穩(wěn)定狀態(tài),且存在鞍結(jié)分岔及跳躍現(xiàn)象。圖1(c)為復(fù)合控制參數(shù)幅頻關(guān)系曲線,對復(fù)合反饋控制系統(tǒng),頻響曲線性質(zhì)發(fā)生完全改變,鞍結(jié)分岔完全消失,只剩與橫軸相交的兩跨臨界分岔點,跳躍現(xiàn)象、突出部分完全消失,系統(tǒng)振幅被較大抑制,復(fù)合控制效果明顯。圖1(d)為η=0.05時最優(yōu)化控制器作用的幅頻關(guān)系曲線,頻響曲線性質(zhì)發(fā)生完全改變,鞍結(jié)分岔完全消失,只剩與橫軸相交的兩跨臨界分岔點;跳躍現(xiàn)象、突出部分完全消失,系統(tǒng)振幅被大幅抑制,振動峰值低于圖1(a)、(b)、(c),減振效果明顯。
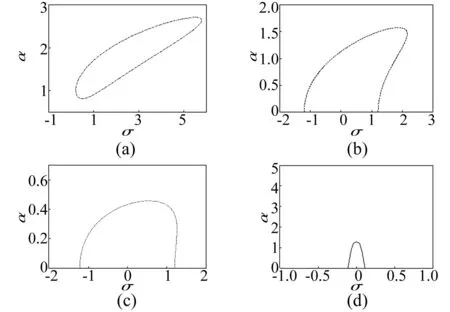
圖1 非線性振動系統(tǒng)幅頻曲線圖像(F=2.5) Fig.1 Amplitude-frequency curves of the nonlinear vibration system(F=2.5)
有、無控制對比見圖2。由圖2看出,通過最優(yōu)化計算可獲得最佳控制參數(shù),對1/2主參數(shù)共振幅值起到明顯抑制作用。系統(tǒng)振動的多值性及分岔可通過選擇適當(dāng)?shù)姆蔷€性反饋增益消除。
調(diào)節(jié)參數(shù)不同時最優(yōu)化控制對應(yīng)解見圖3。由圖3看出,幅頻曲線存在單值現(xiàn)象,均為穩(wěn)定解,且峰值較小。系統(tǒng)振動的多值性及分岔可通過選擇適當(dāng)?shù)姆蔷€性反饋增益消除。通過選擇最佳控制參數(shù),實現(xiàn)非線性振動最優(yōu)化控制。
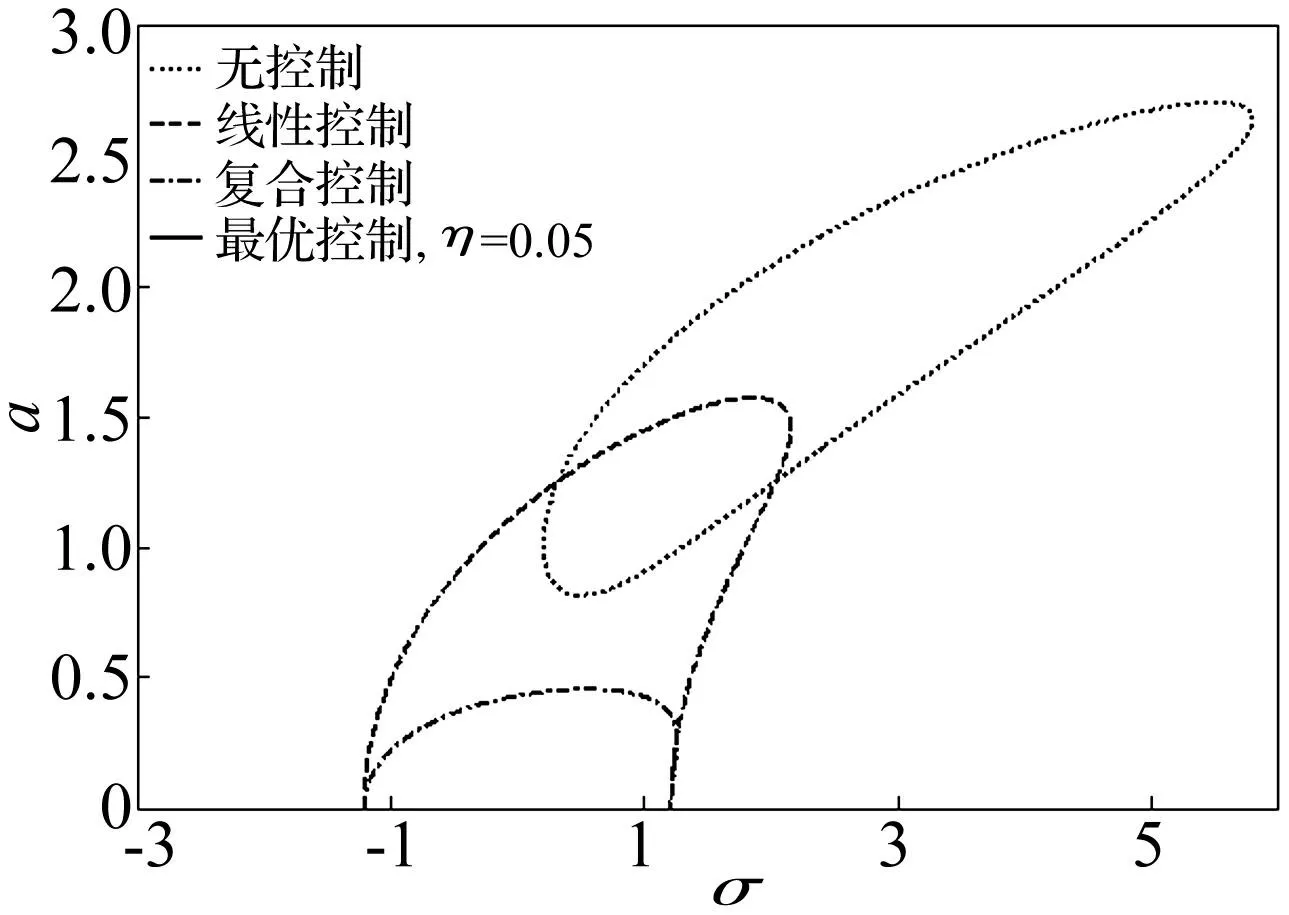
圖2 非線性振動系統(tǒng)減振幅頻-響應(yīng)幅值圖像 Fig.2 Reduction of the amplitude-frequency curves of the nonlinear vibration system
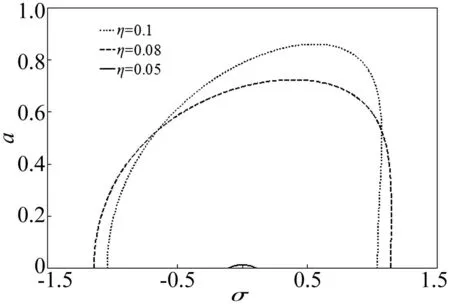
圖3 非線性振動系統(tǒng)減振激勵幅頻-響應(yīng)幅值圖像 Fig.3 Reduction of the amplitude-frequency curves of the nonlinear vibration system with optimal control
6結(jié)論
(1)研究含時滯的非線性位移反饋及非線性速度反饋的Duffing-Van der Pol振子主參數(shù)共振響應(yīng)特性。基于弱非線性、弱反饋控制、弱參數(shù)激勵及小阻尼假設(shè),利用平均法給出確定穩(wěn)態(tài)響應(yīng)振幅、相位的平均方程。
(2)引入非線性反饋增益,使參數(shù)調(diào)節(jié)范圍更廣,調(diào)節(jié)手段更多樣化。利用最優(yōu)化參數(shù)計算方法可獲得最佳控制參數(shù)。
(3)引入約束條件中衰減率調(diào)節(jié)參數(shù),可擴大反饋控制參數(shù)取值范圍。本文控制參數(shù)最優(yōu)化計算方法物理意義明確,計算簡便,便于應(yīng)用,具有一定推廣價值。
參考文獻(xiàn)
[1]彭解華,唐駕時,于德介,等. Van der pol-Duffing系統(tǒng)非共振Hopf分叉[J].國防科技大學(xué)學(xué)報,2001,23(2):107- 110.
PENG Jie-hua,TANG Jia-shi,YU De-jie,et al.Nonresonant hopf bifurcation of Van der Pol-Duffing sytem[J]. Journal of National University of Defense Technology,2001,23 (2): 107-110.
[2]許磊,陸明萬,曹慶杰. Van der Pol-Duffing方程非線性動力學(xué)分叉特性研究[J].應(yīng)用力學(xué)學(xué)報,2002,19(4):130-133.
XU Lei,LU Ming-wan,CAO Qing-jie.Nonlinear dynamical bifurcation analysis of Van der Pol-Duffing equation[J]. Chinese Journal of Applied Mechanics, 2002,19(4):130-133.
[3]甘春標(biāo),陸啟韶,黃克累. 耦合Duffing-Van der Pol振子的強共振分叉解[J]. 應(yīng)用數(shù)學(xué)和力學(xué),1999,20(1):63-70.
GAN Chun-biao, LU Qi-shao, HUANG Ke-lei.Strongly resonant bifurcations of nonlinearly coupled Van der Pol-Duffing oscillator[J]. Applied Mathematics and Mechanics, 1999, 20 (1): 63-70.
[4]陳予恕,徐鑒. Van der Pol-Duffing-Mathieu型系統(tǒng)主參數(shù)共振分岔解的普適分類[J]. 中國科學(xué)A輯,1995,25(12): 1287-1297.
CHEN Yu-shu, XU Jian. Van der Pol type-Duffing-Mathieu system primary parameter resonance bifurcation solution of the general classification[J].Science in China Series A,1995, 25 (12): 1287-1297.
[5]黃志龍,孫志鋒. 諧和激勵下強非線性杜芬-范德波振子的響應(yīng)[J]. 浙江大學(xué)學(xué)報:工學(xué)版,2005,39(3):445-448.
HUANG Zhi-long,SUN Zhi-feng.Responses of Duffing- van der Pol oscillator with strong nonlinearity subject to harmonic excitation[J]. Journal of Zhejiang University: Engineering Science, 2005, 39 (3): 445-448.
[6]褚衍東,李險峰,張建剛. Van der Pol-Duffing 耦合系統(tǒng)的分岔與混沌控制[J]. 江南大學(xué)學(xué)報:自然科學(xué)版,2007, 6(1):119-123.
CHU Yan-dong,LI Xian-feng,ZHANG Jian-gang.Chaos controlling and bifurcation of Van der Pol-Duffing system [J]. Journal of Southern Yangtze University:Natural Science Edition, 2007, 6 (1): 119-123.
[7]Attilio M. Approximate solution of a class of nonlinear oscillators in resonance with a periodic excitation[J]. Nonlinear Dynamics, 1998, 15 (4): 329-343.
[8]Xu J, Chung K W. Effects of time delayed position feedback on a Van der Pol-Duffing oscillator[J]. Physica D: Nonlinear Phenomena, 2003, 180 (1/2): 17-39.
[9]Hu H Y, Wang Z H. Stability analysis of damped SDOF systems with to time delays in state feedback[J]. Journal of Sound and Vibration,1998,214(2):213-225.
[10]Wang Z H, Hu H Y. Delay-independent stability of retarded dynamic systems of multiple degrees of freedom[J]. Journal of Sound and Vibration,1999,226(1):57-71.
[11]王在華,李俊余. 時滯狀態(tài)正反饋在振動控制中的新特征[J].力學(xué)學(xué)報,2010,42(5):933-942.
WANG Zai-hua,LI Jun-yu.New features of the time-delayed positive feedback control[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010,42(5): 933-942.
[12]蔡國平,陳龍祥. 時滯反饋控制的若干問題[J].力學(xué)進(jìn)展,2013,43(1):21-28.
CAI Guo-ping,CHEN Long-xiang.Some problems of the delayed feedback control[J]. Advances of Mechanics, 2013, 43(1):21-28.
[13]趙艷影,徐鑒. 時滯非線性動力吸振器的減振機理[J]. 力學(xué)學(xué)報,2008,40(1):98-106.
ZHAO Yan-ying, XU Jian.Mechanism analysis of the nonlinear vibration of absorbers[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008,40(1):98-106.
[14]趙艷影,徐鑒. 利用時滯反饋控制自參數(shù)振動系統(tǒng)的振動[J]. 力學(xué)學(xué)報,2011,43(5):894-903.
ZHAO Yan-ying,XU Jian.Using the delayed feedback to control the vibration of the auto-parametric dynamical systems[J]. Chinese Journal of Theoretical and Applied Mechanics,2011,43(5):894-903.
[15]周加喜,徐道臨,李盈利,等. 基于最優(yōu)時延反饋控制的主-被動非線性隔振方法研究[J]. 振動工程學(xué)報, 2011,24(6): 639-645.
ZHOU Jia-xi,XU Dao-lin,LI Ying-li,et al.An active-passive nonlinear vibration isolation method based on optimal time-delay feedback control[J]. Journal of Vibration Engineering, 2011,24(6):639-645.
[16]Tsuda Y, Tamura H, Sueoka A, et al. Chaotic behaviour of a nonlinear vibrating system with a retarded argument[J]. JSME International Journal, Ser. 3, 1992, 35 (2): 259-267.
[17]Li X Y, Ji J C, Hansen C H, et al. The response of a Duffing-Van der Pol oscillator under delayed feedback control[J]. Journal of Sound and Vibration,2006, 291: 644-655.
[18]李欣業(yè),陳予恕,吳志強,等. 參數(shù)激勵Duffing-Van der Pol 振子的動力學(xué)響應(yīng)及反饋控制[J]. 應(yīng)用數(shù)學(xué)和力學(xué),2006,27(12):1387-1396.
LI Xin-ye,CHEN Yu-shu,WU Zhi-qiang,et al.Response of a parametrically excited Duffing-Van der Pol oscillator with delayed feedback[J]. Applied Mathematics and Mechanics,2006, 27(12): 1387-1396.
[19]楊平. Van der Pol-Duffing 系統(tǒng)共振雙Hopf分岔[J]. 淮海工學(xué)院學(xué)報:自然科學(xué)版,2008,17(2):42-62.
YANG Ping.Resonant double hopf bifurcation of Van der Pol-Duffing system[J]. Journal of Huaihai Institute of Technology:Natural Science Edition,2008,17(2):42-62.
[20]Nayfeh A H, Chin C, Nayfeh S A. Nonlinear normal modes of a cantilever beam[J]. Journal of Vibration and Acoustics, 1995, 117(4): 477-481.
[21]Nayfeh A H. Perturbation methods[M]. New York: Wiley, 1973.



