兩級階梯形變幅桿設計及優化

第一作者申昊男，博士生，1988年9月生

通信作者郁鼎文男，教授，1962年10月生

兩級階梯形變幅桿設計及優化

申昊，蔡萬寵，郁鼎文

(清華大學機械工程學系，北京100084)

摘要：基于ANSYS workbench多目標驅動優化模塊對兩級階梯形變幅桿進行優化設計。基于解析法設計兩級階梯形變幅桿，建立參數化變幅桿模型；在靜力學分析基礎上對變幅桿進行模態、諧響應分析。通過52個設計點仿真分析獲得諧振頻率、放大系數、最大應力與變幅桿結構尺寸關系，并優化變幅桿尺寸。研究表明，變幅桿諧振頻率小于理論設計頻率，振幅放大系數小于理論值，超聲能量損耗較大。優化所得變幅桿的諧振頻率接近理論設計頻率，提高放大系數。為大功率、大振幅的超聲變幅桿優化設計提供新的設計、優化思路。

關鍵詞：階梯形變幅桿；多目標驅動優化；放大系數；諧振頻率；超聲加工

基金項目：國家自然科學基金(51475260)；北京市科技項目(D131100002713003)

收稿日期：2014-06-03修改稿收到日期：2014-09-12

中圖分類號:TG663

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.20.018

Abstract:A two-section ultrasonic stepped horn was designed and optimized using the multi-goal driven optimization method based on ANSYS workbench. Based on analytical method, the two-section ultrasonic stepped horn was designed and a parameterized model of the horn was established. In addition, the amplifying rate and resonant frequency of the horn were obtained by using static, modal and harmonic response analyses. A simulation with fifty-two design points selected was carried out, and the relationship between vibration parameters and sizes of the horn was obtained. Moreover, the sizes of the ultrasonic horn were optimized using the multi-goal driven optimization method. The results show that the real resonant frequency is lower than the theoretically designed frequency and the real amplifying rate of the horn inclines to be smaller than the theoretical one. Through optimization, the deviation between the real resonant frequency and theoretically designed frequency is reduced, and the amplifying rate is improved. The paper provides a new optimal design method of ultrasonic horn in high-power ultrasonic machining.

Design and optimization of two-section ultrasonic stepped horn

SHENHao,CAIWan-chong,YUDing-wen(Department of mechanical engineering, Tsinghua University, Beijing 100084, China)

Key words:two-section ultrasonic stepped horn; multi-goal driven optimization; amplifying rate; resonant frequency; ultrasonic machining

超聲加工系統主要由超聲波發生器、換能器及變幅桿等組成。變幅桿起放大換能器輸出機械振動振幅、聚集超聲振動能量及超聲振動系統阻抗匹配等作用，其聲學振動特性對整個超聲加工裝置均極其重要[1-2]。而減小變幅桿超聲能量傳遞損失、提高放大系數已成超聲振動系統研究熱點。Amin等[3]將有限元方法用于超聲變幅桿設計，優化變幅桿曲線形狀、提高超聲加工材料去除率。張可昕等[4]用有限元法設計帶加工工具的復合變幅桿，分析刀具尺寸對變幅桿放大倍數、諧振長度影響，優化獲得變幅桿最佳放大倍數及諧振長度。

隨旋轉超聲技術在脆性材料加工中廣泛應用，為提高效率及質量對旋轉超聲加工系統振幅、頻率等輸出參數要求更高。因此，設計大放大系數超聲變幅桿、提高能量轉換效率非常必要[5]。目前普遍使用的變幅桿設計方法有解析法[6]、傳輸矩陣法[7]、四端網絡法[8]、表觀彈性法[9]及有限元法[10-11]等。

本文基于解析法設計兩級階梯形變幅桿，并通過模態、諧響應分析獲得理論計算偏差；基于ANSYS workbench建立參數化變幅桿模型，用多目標驅動優化方法分析其結構尺寸對放大系數、最大等效應力等參數影響規律，優化結構尺寸。

1變幅桿設計

由于本文設計的變幅桿應用對象為深腔零件，軸向尺寸較大，故用兩級階梯形。基于特殊工程背景，刀具頭長度對變幅桿振動特性影響較大。設計時考慮該長度對變幅桿諧振特性影響，將球頭刀具作為第二級階梯形變幅桿輸出級，簡化刀具與變幅桿結合面特性進行一體化設計，使刀具末端振幅最大，見圖1。

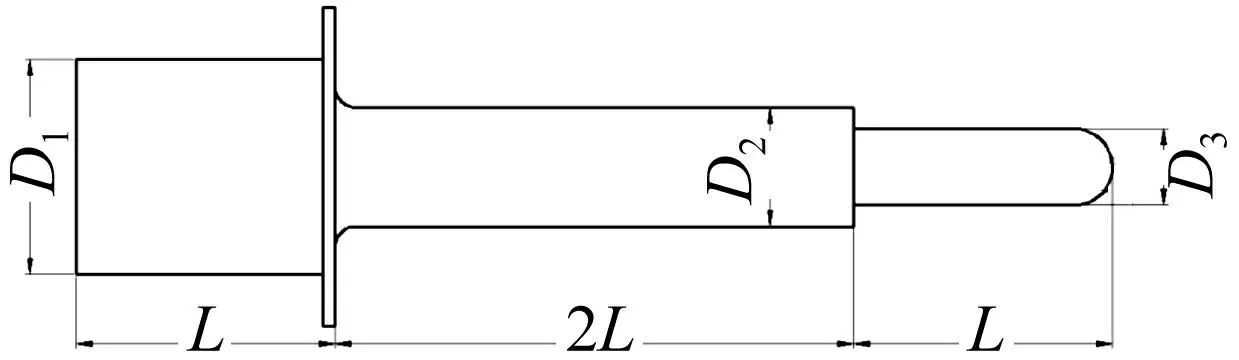
圖1　兩級階梯形變幅桿 Fig.1 Two-section ultrasonic stepped horn

利用半波長理論進行變幅桿設計，其頻率為20 kHz，材料45號鋼。在諧振條件下，變幅桿縱振波動方程[12]為

(1)

式中：A為變幅桿截面積函數；ξ為質點位移函數；k=ω/c為圓波數，c為縱波在變幅桿中傳播速度。

超聲振動系統一般在變幅桿節面位置固定，為考慮變幅桿定位、夾緊對其振動特性影響，在理論節面位置設計圓盤。用ANSYS workbench DM模塊建立參數化模型(圖1)，變幅桿結構尺寸見表1。

表1　變幅桿參數

2變幅桿振動特性仿真分析

2.1模態分析

超聲振動系統一般在變幅桿節面位置固定，變幅桿圓盤后面及圓周面會與固定支架配合，而前面會通過夾緊力夾緊。為研究定位、夾緊對變幅桿振動特性影響對其進行靜力學分析，獲得其在安裝條件下的預應力。設變幅桿約束形式見圖2，圓盤后面軸向位移及圓周面徑向位移均為0，圓盤前面施加預緊力，據超聲設計手冊，設預緊力為10 000 N。

圖2　變幅桿約束形式 Fig.2 The constrain of ultrasonic horn

在頻率18～22 kHz范圍內對變幅桿進行模態分析，獲得變幅桿5階模態，頻率、振動形式見表2，前3階模態振型見圖3。

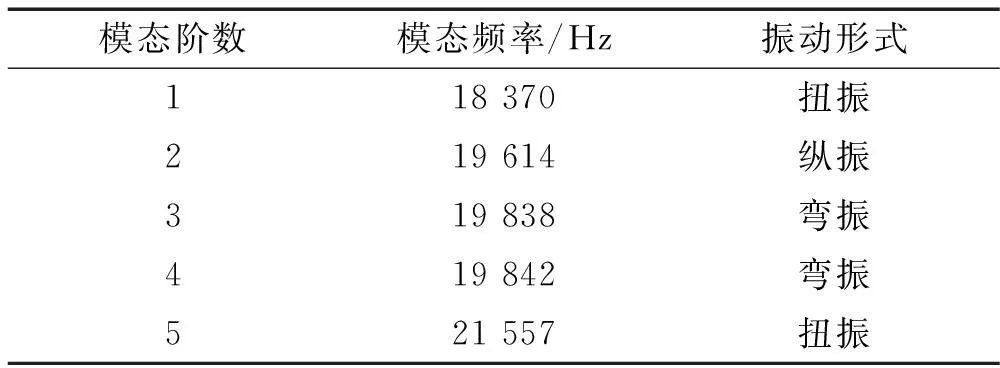
表2　各階模態頻率及振動形式

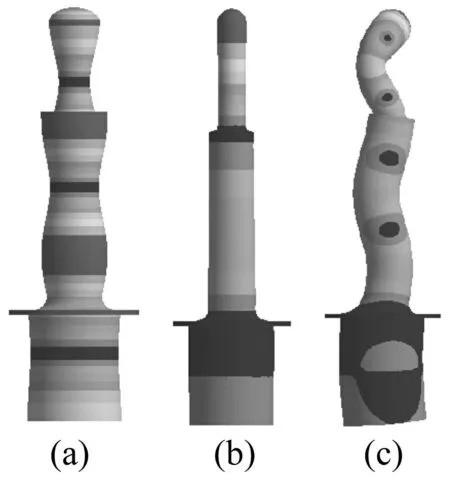
圖3　前3階模態振型 Fig.3 The first three modes of ultrasonic horn

由模態分析結果知，變幅桿縱振諧振頻率為f，=19 614 Hz，小于理論設計頻率20 kHz。為對比分析變幅桿節面預應力對其振動特性影響，對不固定的變幅桿進行模態分析，獲得其縱振諧振頻率為f，=19 457 Hz。原因為：①理論設計時未考慮圓盤存在，圓盤設計使變幅桿諧振頻率減小；②安裝預應力使變幅桿諧振頻率發生偏移；③變幅桿采用一維設計理論，忽略泊松效應引起的橫向振動，與實際振動情況存在偏差。

2.2諧響應分析

為研究變幅桿放大系數、應力分布，在頻率18～22 kHz范圍內對其進行諧響應分析，分別以100個頻率的簡諧激勵作為輸入，獲得變幅桿輸出振幅及最大等效應力，并繪制頻率響應曲線，見圖4、圖5。由兩圖可知，隨激勵頻率變化最大應力及振幅變化規律相似，二者在模態頻率點取得極值，模態頻率小于理論設計頻率，即變幅桿實際諧振頻率小于理論設計頻率。

以振幅4 μm，頻率20 kHz的簡諧振動作為輸入時變幅桿輸出振幅、放大系數及最大等效應力見表3。沿變幅桿軸線振幅分布曲線見圖6。測量獲得變幅桿節點位置為57.79 mm，較解析解x0=64.625 mm節點位置向大端偏移。因激勵頻率大于變幅桿實際諧振頻率，超聲振動在桿中傳播的半波長減小，故節點位置向大端偏移。節點位置為超聲振動系統固定點，其偏移將導致系統固定處出現較大縱振振幅，導致較大超聲能量損耗，增大系統發熱量及桿最大等效應力。

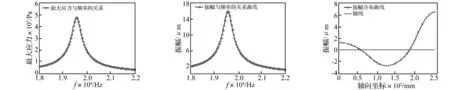
圖4 最大應力頻率響應曲線Fig.4Frequencyresponseofstress圖5 振幅頻率響應曲線Fig.5Frequencyresponseofamplitude圖6 階梯形變幅桿振幅分布曲線Fig.6Thecurveofamplitude

表3　激勵頻率f=20 kHz時變幅桿振動參數

3變幅桿優化設計及驗證

3.1多目標驅動優化設計

模態分析及諧響應分析結果表明，解析解所得兩級階梯形變幅桿實際諧振頻率小于理論設計頻率，實際節面位置向桿的大端偏移。為優化變幅桿結構尺寸，獲得較優諧振頻率、節點位置及振幅放大系數，本文用多目標驅動優化方法對兩級階梯形變幅桿第一級尺寸進行優化設計。優化目標為：放大系數最大化，最大應力最小化，振動形式確認系數近似等于泊松比。設計大、小端長度等5個輸入變量，并限定變量取值范圍，見表4。將仿真計算所得刀具輸出端X、Y、Z方向振幅及變幅桿輸入端Z方向振幅、最大應力設為輸出變量，見表5。

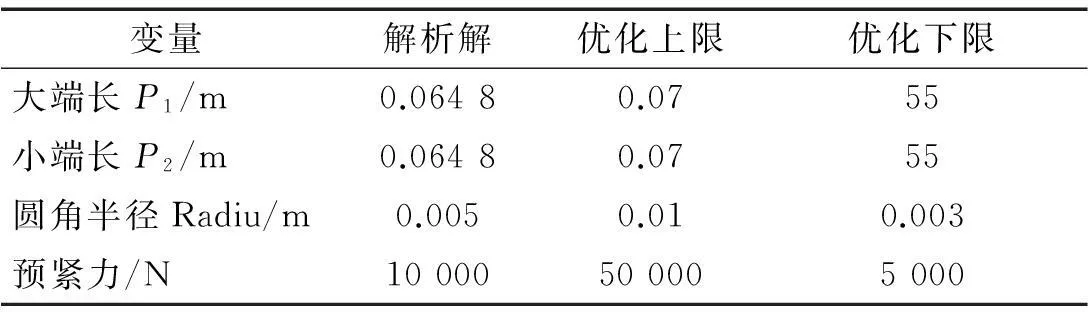
表4　輸入變量

表5　輸出變量設計

由于ANSYS中無法自動捕獲變幅桿振動形式，變幅桿尺寸改變時若其振動形式改變，則可能在其它振動形式下得到放大系數極大值與最大應力極小值。因此，不能簡單將振幅放大系數與最大應力作為優化設計目標。為避免變幅桿振動形式改變導致優化失敗，進行設置，獲得導出變量見表6。

表6　導出變量設計

(1)優化設計中為確定變幅桿在20 kHz處的振動形式仍為縱振，本文設計導出變量振動形式確認系數，其值接近泊松比時可確定變幅桿振動形式為縱振。

(2)基于刀具輸出端、變幅桿輸入端Z向振幅，計算變幅桿放大系數作為優化設計目標變量。

基于以上輸入變量、輸出變量及導出變量，ANSYS多目標驅動優化設計模塊應用中心復合表面設計算法(central composite face-centered design)建立52個變幅桿設計點。該方法會據設計變量數量指數型增加設計點數。設計點分布見圖7，圖中已標明前40個設計點的分布曲線。

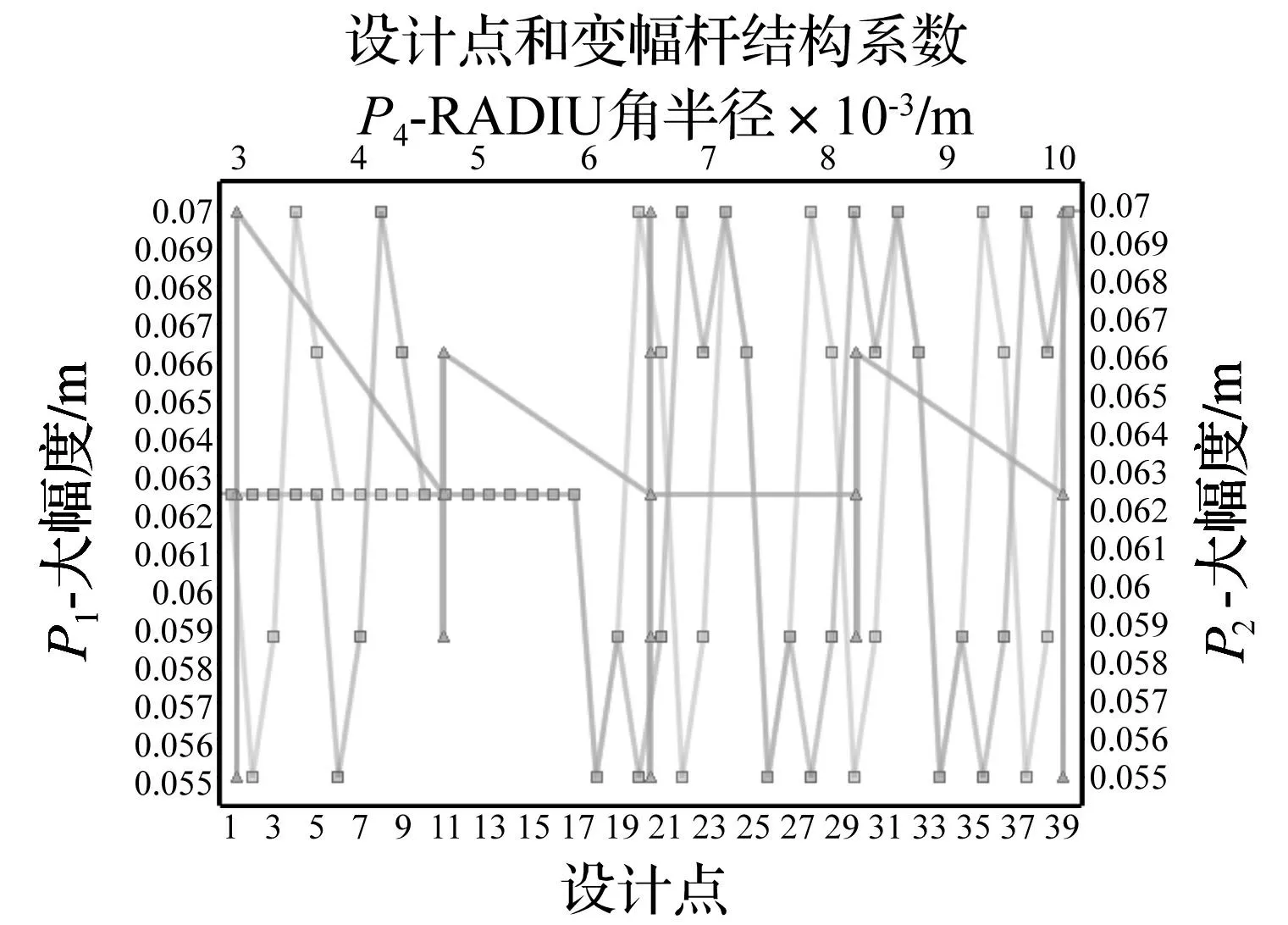
圖7　優化設計點分布圖 Fig.7 Distribution of design points

通過對52個設計點仿真分析，建立振幅放大系數及最大應力等變量與變幅桿尺寸變量響應面，獲得目標變量對變幅桿尺寸變化的敏感程度。優化設計流程見圖8。

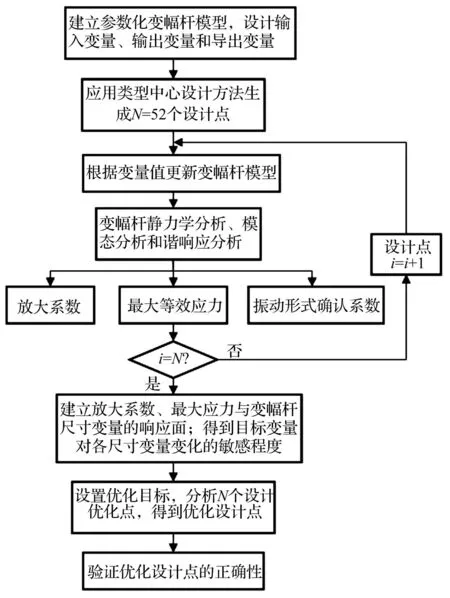
圖8　多目標驅動優化流程圖 Fig.8 Flow chart of multi-goal driven optimization

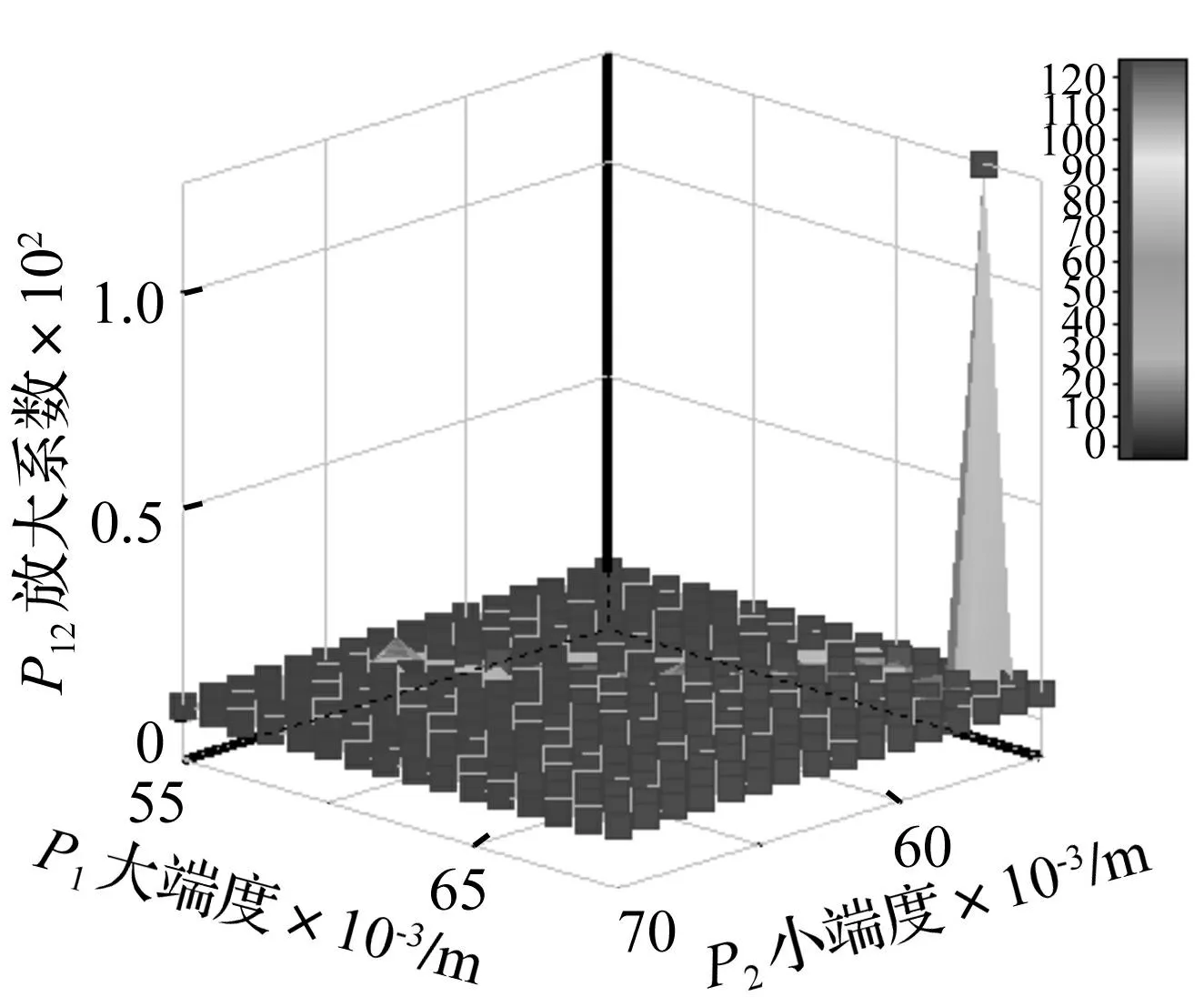
圖9　放大系數與變幅桿尺寸響應面 Fig.9 Response chart for the amplifying rate and the sizes of horn

放大系數與變幅桿大、小端長度響應面見圖9。由圖9看出，變幅桿尺寸接近最優值時放大系數顯著增大，出現峰值，即變幅桿尺寸存在最優值。

最大應力與變幅桿大、小端長度響應面見圖10。由圖10看出，變幅桿大端長度對最大應力影響較大。

輸出變量對輸入變量變化的敏感度曲線見圖11。由圖11看出，圓角半徑及預緊力對變幅桿放大倍數、最大等效應力影響較小。因此，優化后可保持變幅桿圓角半徑及預緊力大小不變。

據52個設計點的仿真分析結果，以放大系數、最大應力和振動形式確認系數為目標變量，以掃掠方式得到優化設計點。優化后的變幅桿參數圓整值見表7。

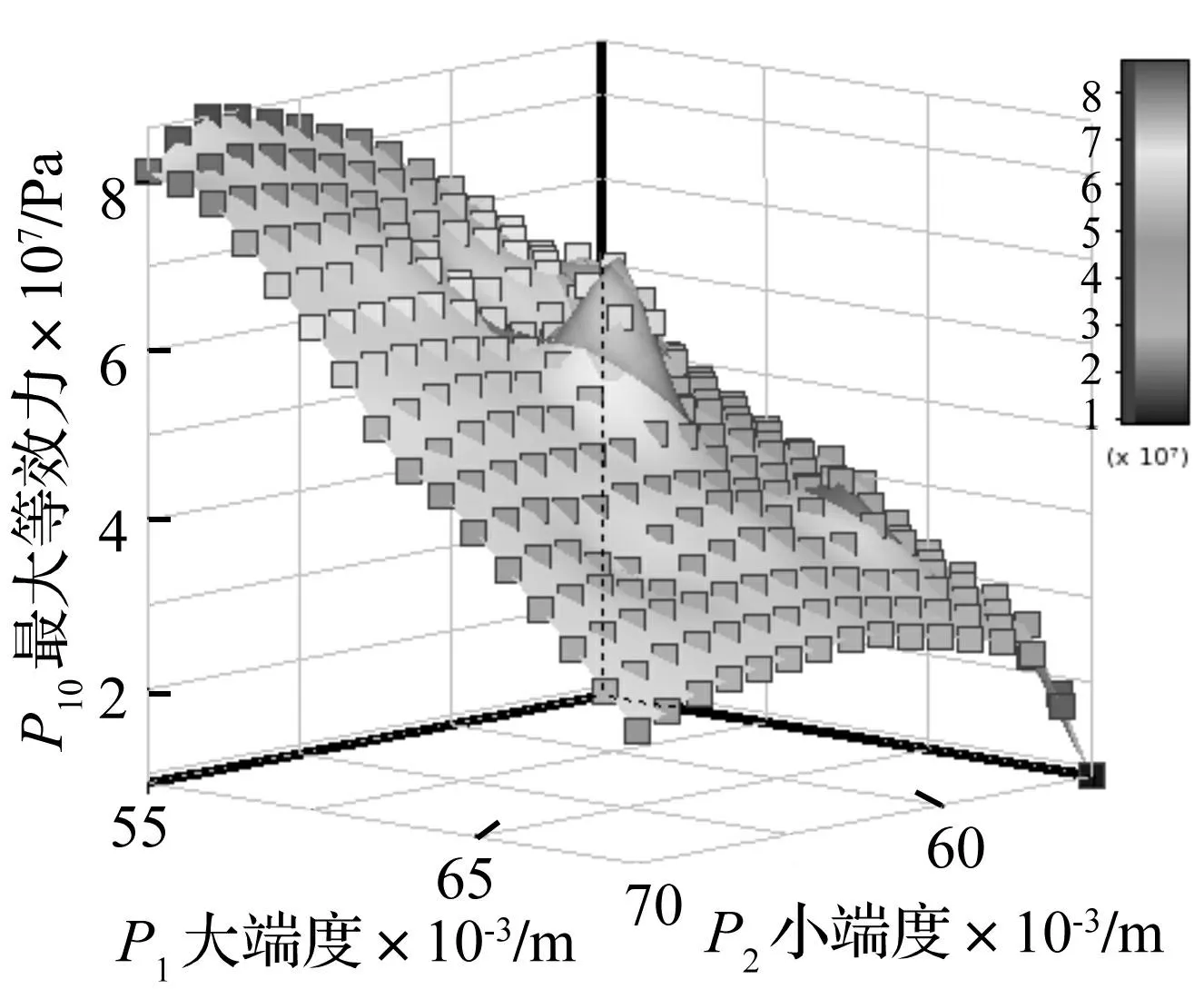
圖10　最大等效應力與變幅桿尺寸響應面 Fig.10 Response chart for the maximum stress and the sizes of horn

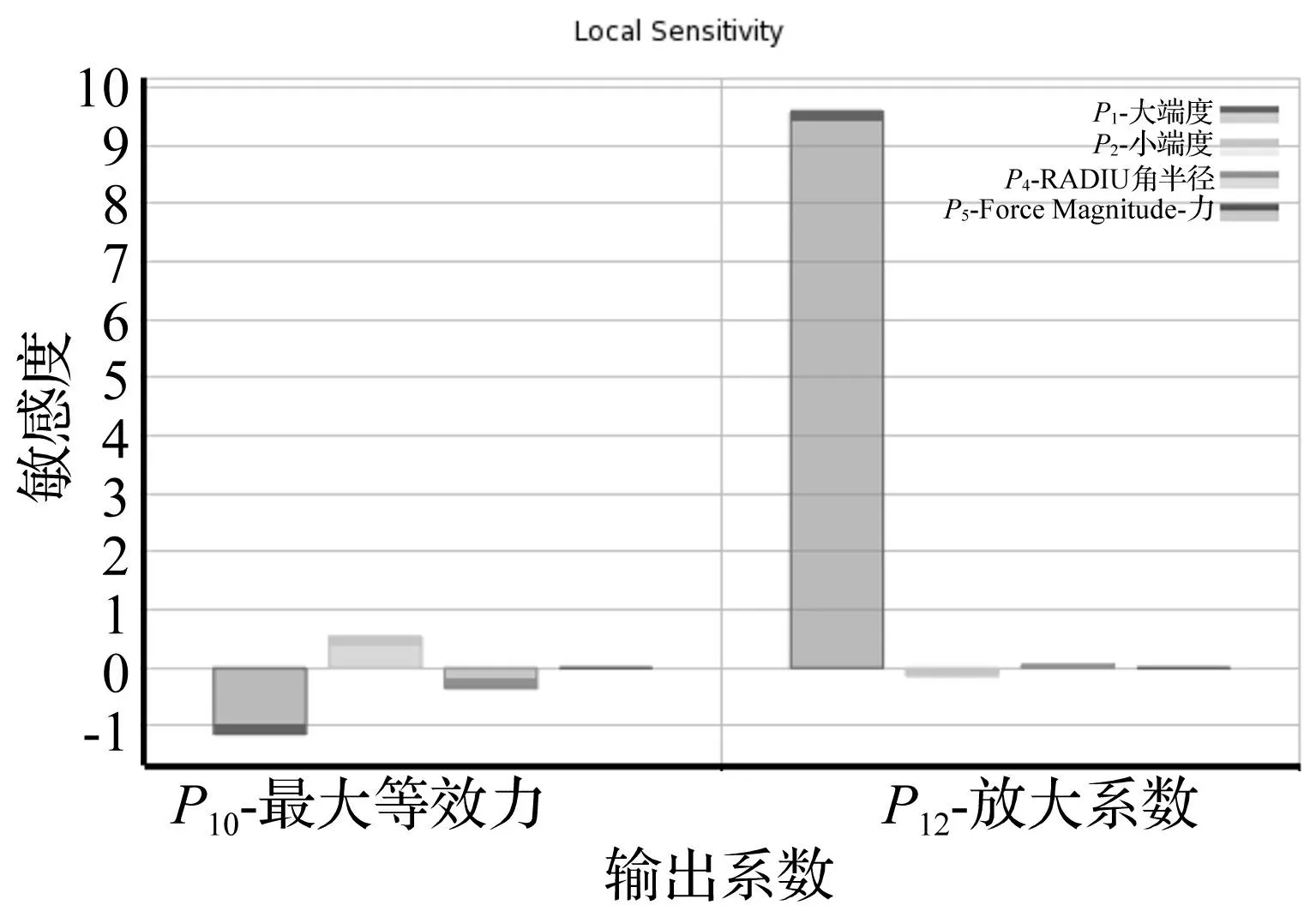
圖11　輸出變量對輸入變量敏感度 Fig.11 Local sensitivity of the output variables to input variables

諧振頻率f/Hz大端長度/mm小端長度/mm圓角半徑/mm節面距大端距離/mm2004068581065

3.2驗證優化設計點正確性

為驗證多目標驅動優化方法所得優化設計點的正確性，對解析求解的變幅桿及優化后變幅桿進行對比分析。先對變幅桿進行靜力學分析，并以此為基礎進行模態及諧響應分析，獲得優化前后變幅桿的諧振頻率、放大系數及最大應力見表8。由表8看出，優化后的變幅桿諧振頻率接近理論設計頻率20 kHz，放大系數較優化前有明顯提高，且最大應力在45號鋼強度極限內。因此，本文優化法不僅能優化變幅桿尺寸，使其實際諧振頻率接近理論設計頻率，且能提高超聲能量傳輸效率，為大功率、大振幅超聲加工奠定基礎。

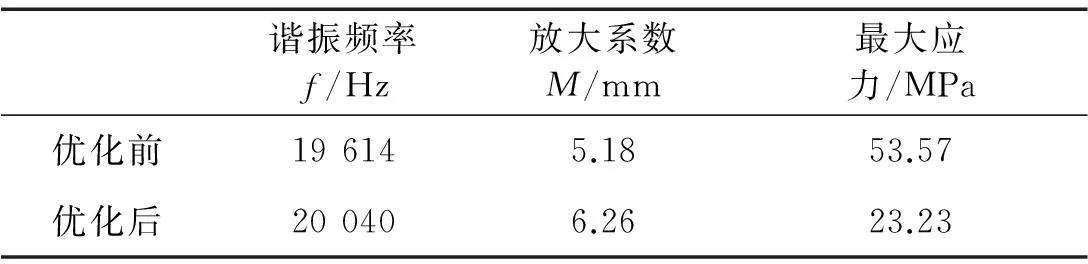
表8　優化前后變幅桿振動特性對比

4結論

本文基于解析法設計兩級階梯形變幅桿并建立模型，仿真分析獲得其模態頻率、最大應力、放大系數及節點位置。基于多目標驅動優化方法，考慮安裝、夾緊影響優化變幅桿結構尺寸，結論如下：

(1)利用解析法設計所得兩級階梯形變幅桿諧振頻率小于理論設計頻率，節點位置向大端偏移，振幅放大系數減小。

(2)多目標驅動優化設計方法能有效優化變幅桿結構尺寸使其實際諧振頻率接近理論設計頻率及提高振幅放大系數。可為大功率、大振幅超聲加工提供技術支持。

(3)考慮安裝、夾緊對變幅桿振動特性影響時較接近其實際工作情況，對變幅桿設計、生產、安裝有一定指導意義。

參考文獻

[1]趙明利,程雪利,趙波. 帶工具頭超聲變幅桿節點定位偏差問題分析[J]. 聲學技術, 2013, 32(3): 253-256.

ZHAO Ming-li, CHENG Xue-li, ZHAO Bo. Research on the node localization deviation of the ultrasonic amplitude transformer with tool head[J]. Technical Acoustics, 2013, 32(3): 253-256.

[2]張向慧,錢樺. 旋轉超聲加工振動系統的研究[J]. 振動與沖擊, 2010, 29(4): 218-221.

ZHANG Xiang-hui, QIAN Hua. Research on the vibration system of Rotary ultrasonic machining[J]. Journal of Vibration and Shock, 2010, 29(4): 218-221.

[3]Amin S G, Ahmed M H M, Youssef H A. Computer-aided design of acoustic horns for ultrasonic machining using finite-element analysis[J]. Journal of Materials Processing Technology, 1995, 55(3): 254-260.

[4]張可昕,張向慧,高炬,等. 帶有加工工具的超聲復合變幅桿的優化設計[J]. 機械設計與制造, 2011(11):38-40.

ZHANG Ke-xin, ZHANG Xiang-hui, GAO Ju, et al. Ptimum design of acoustic horns with tool for ultrasonic machining using finite-element analysis[J]. Machinery Design & Manufacture, 2011(11):38-40.

[5]潘巧生,劉永斌,賀良國,等. 一種大振幅超聲變幅桿設計[J]. 振動與沖擊, 2014, 33(9): 1-5.

PAN Qiao-sheng, LIU Yong-bin, HE Liang-guo, et al. Design of an ultrasonic horn with high amplitude of longitudinal vibration [J]. Journalof Vibration and Shock, 2014, 33(9): 1-5.

[6]賀西平,高潔. 超聲變幅桿設計方法研究[J]. 聲學技術, 2006, 25(1): 82-86.

HE Xi-ping, GAO Jie. A review of ultrasonic solid horn design [J]. Technical Acoustics, 2006, 25(1): 82-86.

[7]Lesniewski P. Discrete component equivalent circuit for webster shorns[J]. Applied Acoustics, 1995, 44: 117-124.

[8]高潔,賀西平,胡靜. 四端網絡法統一變幅桿的性能參量[J]. 聲學技術, 2006, 25(1): 87-89.

GAO Jie, HE Xi-ping, HU Jing. Unified treatment of ultrasonic horn characteristics based on four-end network approach [J]. Technical Acoustics, 2006, 25(1): 87-89.

[9]Mori E. New bolt clamped flexural mode ultrasonic high-power transducer with one dimensional construction [C]. Ultrasonics International Conf. Proc.,1989: 257-261.

[10]薛庚健,馬麟, 李亞潔. 階梯形變幅桿的設計分析[J]. 機械設計與制造, 2013, 12: 14-16.

XUE Geng-jian, MA Lin, LI Ya-jie. Steppedultrasonic transformers design and analysis[J]. Machinery Design & Manufacture, 2013, 12: 14-16.

[11]Huang Yi-cheng, Ding Guan-zhang, Chen Bo-hsuan,et al. Simulation and experiment of langevin-type piezoelectric ultrasonic horn for micro tool motion[J]. Intelligent Technologies and Engineering Systems, 2013, 234: 967-974.

[12]曹鳳國.超聲加工技術[M].北京:化學工業出版社, 2005.