基于人工蜂群算法的電子商務(wù)多Agent自動談判模型

網(wǎng)絡(luò)出版地址：http://www.cnki.net/kcms/detail/23.1538.tp.20150508.0916.001.html

基于人工蜂群算法的電子商務(wù)多Agent自動談判模型

高珊，馬良，張惠珍

(上海理工大學(xué) 管理學(xué)院，上海 200093)

摘要：由于現(xiàn)有電子商務(wù)自動談判模型在不斷動態(tài)變化的網(wǎng)絡(luò)環(huán)境中匹配慢、整體效用值低，結(jié)合人工蜂群算法的原理及求解流程，給出一種電子商務(wù)自動談判模型。該模型基于多Agent多屬性的自動談判模式，融合符合實(shí)際的商務(wù)談判方式，著重將電子商務(wù)自動談判的Agent匹配與人工蜂群算法求解的過程相結(jié)合，以快速準(zhǔn)確獲得使整體利益最大的解。通過求解一個電子采購實(shí)例并與其他算法的求解效率進(jìn)行對比，驗證了該模型的有效性。

關(guān)鍵詞：電子商務(wù)；自動談判；人工蜂群算法；多Agent；談判模型

DOI:10.3969/j.issn.1673-4785.201405023

中圖分類號：TP301.6; C93 文獻(xiàn)標(biāo)志碼：A

收稿日期：2014-05-10. 網(wǎng)絡(luò)出版日期：2015-05-08.

基金項目：國家自然科學(xué)基金資助項目(71401106)；上海高校一流學(xué)科建設(shè)計劃項目(S1201YLXK)；上海高校青年教師培養(yǎng)資助計劃項目(SLG12010)；上海市教育委員會科研創(chuàng)新項目(14YZ090)；高等學(xué)校博士學(xué)科點(diǎn)專項科研基金聯(lián)合資助課題(20123120120005).

作者簡介：

中文引用格式：高珊，馬良，張惠珍. 基于人工蜂群算法的電子商務(wù)多Agent自動談判模型[J]. 智能系統(tǒng)學(xué)報, 2015, 10(3): 476-481.

英文引用格式：GAO Shan, MA Liang, ZHANG Huizhen. Multi-Agent automated negotiation model for E-commerce based on the artificial bee colony algorithm[J]. CAAI Transactions on Intelligent Systems, 2015, 10(3): 476-481.

Multi-Agent automated negotiation model for E-commerce

based on the artificial bee colony algorithm

GAO Shan, MA Liang, ZHANG Huizhen

(School of Management, University of Shanghai for Science and Technology, Shanghai 200093, China)

Abstract：Since the current E-commerce automated negotiation systems (ANS) have some disadvantages such as slow matching and low overall utility in the dynamic Internet environment, a kind of E-commerce automated negotiation model based on the theory of the artificial bee colony algorithm (ABC) is presented. The model integrates the intelligent business negotiation way based on the multi-Agent and multi-attribute automated negotiation mode. To obtain the solution that maximizes the overall interests quickly and accurately, the model puts emphasis on combining the Agent matching of the E-commerce automated negotiation with the process of the ABC algorithm solution. A solution to an e-procurement was illustrated and compared with the other algorithms in efficiency, validating the effectiveness of the model.

Keywords：E-commerce; automated negotiation; artificial bee colony algorithm (ABC); multi-Agent; negotiation model

通信作者：高珊. E-mail: gaoshan1158@126.com.

隨著人們對電子商務(wù)交易智能化、個性化需求的提高，實(shí)現(xiàn)電子商務(wù)談判的智能化和個性化已經(jīng)成為下一代電子商務(wù)的發(fā)展方向。目前，電子商務(wù)自動談判的研究已成為多主體系統(tǒng)的典型應(yīng)用之一[1]。相對于傳統(tǒng)的談判支持系統(tǒng)，自動談判可以在一定程度上代替人進(jìn)行談判，能夠優(yōu)化談判過程，提高談判效率，節(jié)約成本。尤其是實(shí)現(xiàn)異地遠(yuǎn)程商務(wù)談判的自動化與決策支持，具有重要的研究價值。

從20世紀(jì)90年代初，國內(nèi)外學(xué)者開始研究電子商務(wù)自動談判模型，陸續(xù)研發(fā)出一些有實(shí)際應(yīng)用價值的自動談判系統(tǒng)，例如有慎思機(jī)制的談判模型、在線拍賣網(wǎng)站AnctionBot系統(tǒng)、具有學(xué)習(xí)能力的談判系統(tǒng)等。隨著Agent的引入，電子商務(wù)談判系統(tǒng)開始有了新的發(fā)展方向。而多個Agent的自動談判技術(shù)彌補(bǔ)了傳統(tǒng)談判信息不對稱的不足，更符合電子商務(wù)談判對速度快、整體效益需求高的要求。現(xiàn)有關(guān)多Agent談判模型和算法的研究較少，并且存在一些不足。諸如：1)現(xiàn)有自動談判模型大都采用一旦發(fā)現(xiàn)Agent相匹配即退出的模式，Agent匹配到的不一定是使整體效用最大的Agent；2)使用較為成熟的智能算法，如模擬退火算法[1]、遺傳算法[2]、貝葉斯學(xué)習(xí)或建立效用函數(shù)等，而一些新興算法如蝙蝠算法、人工魚群算法、人工蜂群算法等尚未用到，這些新興算法在解決實(shí)際問題中有其自身優(yōu)勢；3)基于傳統(tǒng)經(jīng)典理論的談判算法具有很強(qiáng)的針對性，應(yīng)用在不確定性很大的網(wǎng)絡(luò)環(huán)境中有一定困難。針對上述現(xiàn)有電子商務(wù)自動談判模型的局限性，本文引入了新的模型和求解算法來解決上述問題。

2005年，Karaboga提出了一種基于蜜蜂群體覓食行為的群智能優(yōu)化算法—人工蜂群算法(artificial bee colony algorithm, ABC)。該算法參數(shù)較少，全局收斂性也較好，適用于多維問題的求解。ABC算法模擬蜂群的集體行為，蜜蜂群依據(jù)各自分工不同進(jìn)行不同活動，通過交換信息來尋找最佳蜜源。蜂群算法的算法流程與多Agent系統(tǒng)的自動談判模型有一定的相似性，如蜜蜂尋找含蜜量多的蜜源，相當(dāng)于Agent尋找與之匹配的Agent；蜜蜂多次探索尋找全局最優(yōu)解，相當(dāng)于Agent匹配到使整體效用最大的Agent。而且基于蜂群算法的算法流程與多Agent系統(tǒng)的自動談判模型之間的相似性，可以對人工蜂群算法進(jìn)行改進(jìn)，并添加學(xué)習(xí)機(jī)制，使之更適用于電子商務(wù)環(huán)境下多Agent自動談判模型的求解。

1電子商務(wù)自動談判

1.1特征選取和內(nèi)容相似度計算

多Agent系統(tǒng)(multi-Agent system, MAS)中，每一個Agent是獨(dú)立和自治的，不僅要有自主性、反應(yīng)性、能動性、時間連續(xù)性及其個性偏好，還要能夠和其他Agent進(jìn)行交互[4]。在談判過程中，各個Agent相互之間通過競爭、協(xié)商、合作等手段達(dá)到利益最大化的目的。多Agent系統(tǒng)結(jié)構(gòu)有集中式和分布式2種，本文研究分布式結(jié)構(gòu)的多Agent系統(tǒng)。在分布式結(jié)構(gòu)中，Agent之間是平等合作的關(guān)系。自動談判模型中的Agent還應(yīng)該具有如下3個特性：

1)擇優(yōu)選擇。Agent每一次的選擇使得自身效用函數(shù)最大，所有Agent在動態(tài)變化的環(huán)境中選擇的結(jié)果使得整個系統(tǒng)的利益達(dá)到最大。

2)自我學(xué)習(xí)。單個Agent有自己的歷史經(jīng)驗庫、數(shù)據(jù)存儲、處理過程和處理機(jī)，在與整個系統(tǒng)交互的過程中，Agent根據(jù)外界環(huán)境變化的信息，經(jīng)過分析處理反饋出對自己有利的當(dāng)前狀態(tài)，同時更新歷史經(jīng)驗庫和數(shù)據(jù)存儲。即Agent經(jīng)過了自我學(xué)習(xí)的過程。

3)服從協(xié)議。為保證談判過程的正常執(zhí)行，Agent必須執(zhí)行談判協(xié)議規(guī)定的行動方案，使得談判各方解決沖突，最終達(dá)成一致協(xié)議。

1.2Agent屬性的權(quán)重和效用

每個Agent在談判過程中有多個談判屬性，即談判中考慮的問題，每一輪談判中各個屬性的效用值之和是這個Agent在此次談判中所獲得的效用。設(shè)每個Agent有M項屬性，按照自己的偏好對各項屬性分別設(shè)置權(quán)重WM。N個Agent的權(quán)重矩陣為

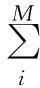
式中：Vij∈(0,10)，i=1,2,…,M，j=1,2,…,N。

對每項屬性的效用值設(shè)定上限和下限，在自動談判過程中每項屬性只能在此范圍內(nèi)進(jìn)行調(diào)整，如式(1)：

(1)

式中：i=1,2,…,M， j=1,2,…,N。

1.3自動談判過程及協(xié)議

電子商務(wù)自動談判過程主要分為6步：需求確定、商品代理(信息搜尋)、商家代理、談判、支付與配送、商品服務(wù)與評價。第2步到第4步為談判系統(tǒng)的核心，也是自動談判系統(tǒng)研究的重點(diǎn)。經(jīng)典的電子商務(wù)多對多談判機(jī)制中交易雙方都有多個，且供應(yīng)方和需求方數(shù)量不一定相等，談判的內(nèi)容不止一項，與現(xiàn)實(shí)生活中的電子商務(wù)市場一致，本文這里研究多對多的多屬性自動談判問題。

首先，確定多對多自動談判協(xié)議。發(fā)起談判時，確定參與談判各方。發(fā)送身份驗證，確認(rèn)談判中用于保障數(shù)據(jù)安全的公鑰和各自的私鑰。談判過程中，采用改進(jìn)讓步協(xié)議[6]，如果當(dāng)前Agent匹配到另外一個Agent的要求，那么就暫時達(dá)成一個協(xié)議。此時若沒有合適當(dāng)前Agent的匹配，則Agent讓步或者進(jìn)入下一輪談判。Agent通過調(diào)整各項屬性的效用值來實(shí)現(xiàn)讓步，并且不能使所有屬性值同時提高，降低一個屬性的效用值，相應(yīng)地提高另一個屬性的效用值。例如，若實(shí)際談判中需方Agent接受較遠(yuǎn)的產(chǎn)地，則相應(yīng)地要求提升產(chǎn)品質(zhì)量，其讓步過程可描述為

式中：x,y∈(0,1)。

如果在某一步中，沒有Agent讓步，那么談判結(jié)束或者協(xié)議指出已經(jīng)產(chǎn)生了一個死鎖。在談判中Agent不能放棄，也不能同時多輪都不變化。在自動談判過程中，如果有Agent無法匹配到其他Agent要求，且經(jīng)過多輪讓步都無法匹配，則該Agent自動退出談判，不影響談判繼續(xù)進(jìn)行。此協(xié)議的優(yōu)點(diǎn)是，它能夠保證收斂或者當(dāng)不能夠收斂時，可以快速結(jié)束談判。在此協(xié)議中，為滿足這個規(guī)則，Agent必須相互知道對方的效用矩陣。

2人工蜂群算法的談判模型設(shè)計

2.1人工蜂群算法基本原理

在蜜蜂群體采蜜的過程中，傳遞蜜源的位置、含蜜量等信息，以便大量蜜蜂飛往優(yōu)秀蜜源采蜜是最重要的部分。因此，人工蜂群算法首先將蜂群分為引領(lǐng)蜂(employed bees)、跟隨蜂(onlookers)和偵察蜂(scouts)3類。出去尋找蜜源的蜜蜂是引領(lǐng)蜂，在舞蹈區(qū)內(nèi)等待選擇蜜源的蜜蜂是跟隨蜂，而在一定情況下進(jìn)行隨機(jī)搜索蜜源的蜜蜂是偵察蜂。蜂群數(shù)量的一半是引領(lǐng)蜂，另一半是跟隨蜂，引領(lǐng)蜂的數(shù)量和食物源的數(shù)量相等。

在蜂群進(jìn)化過程中，引領(lǐng)蜂和跟隨蜂負(fù)責(zé)執(zhí)行開采過程，而偵察蜂執(zhí)行探索過程。蜜蜂執(zhí)行搜索活動的主要過程如下：

1)隨機(jī)初始化引領(lǐng)蜂的位置，發(fā)現(xiàn)初始蜜源并記憶當(dāng)前蜜源位置，根據(jù)記憶的局部信息，在領(lǐng)域范圍內(nèi)搜索新蜜源。根據(jù)蜜源的花蜜數(shù)量選擇最優(yōu)位置。

2)引領(lǐng)蜂通過跳搖擺舞將蜜源信息分享給跟隨蜂，跟隨蜂通過輪盤賭來選擇一個蜜源。再在此蜜源附近利用其記憶中的局部信息選擇一個新蜜源，比較新位置和原位置的花蜜數(shù)量，若新位置的花蜜量高于原位置，則記住新位置。

3)一個食物源經(jīng)過Nlimit代(Nlimit為自定義常量)，其適應(yīng)度都沒有任何改變，則當(dāng)前食物源被放棄，且當(dāng)前食物源處的引領(lǐng)蜂變?yōu)閭刹旆洌㈤_始隨機(jī)搜索新的蜜源。

4)記錄迄今為止最好蜜源，作為全局最優(yōu)解輸出。

人工蜂群算法反饋機(jī)制優(yōu)越，食物源的花蜜量與食物源被選擇的可能性成正比，蜜蜂能及時停止對較差食物源的開采。且蜜蜂能與其他蜜蜂共同分享食物源的信息。這對自動談判過程中，供應(yīng)商的選擇、屬性調(diào)整以及快速尋找匹配Agent的過程具有有益的參考價值。

2.2人工蜂群算法建模及求解

結(jié)合人工蜂群算法原理和Agent自動談判過程，可以假設(shè)供應(yīng)方為食物源，需求方為蜜蜂，每一個供方和需方為一個Agent，食物源的花蜜量由Agent的效用值來決定。設(shè)供方有N個，需方有X個。與電子商務(wù)市場實(shí)際情況相結(jié)合，供應(yīng)方和需求方數(shù)量不一定相等，談判結(jié)果也不一定是供方和需方一一對應(yīng)，因此將N個供方模擬為rN(r=1,2,…,n)個食物源，即每個供方Agent有r次被選擇的機(jī)會，此處r取決于實(shí)際問題的計算規(guī)模，r取值越大，計算結(jié)果趨向于整體效用值更優(yōu)，但是計算時間也越長。

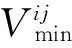
(2)

(3)

式中：βj∈(0,1)為第j個Agent的效用系數(shù)。

計算中，如果需方Agent的屬性值高于當(dāng)前匹配的供方Agent屬性值，則需方Agent的效用系數(shù)βj=0，反之βj=1。若需方Agent的M項屬性中有M1項屬性值低于供方Agent屬性，則βj值用式(4)求解。

(4)

式中：αj∈(0,1)，Wt為屬性值高于當(dāng)前匹配Agent屬性的權(quán)重，Wt為離散集合。

設(shè)引領(lǐng)蜂數(shù)量與需求方數(shù)量相等為X，跟隨蜂數(shù)量也為X。首先，對供方Agent和需方Agent進(jìn)行一次隨機(jī)匹配，將匹配結(jié)果作為引領(lǐng)蜂的初始位置。其次，求出當(dāng)前的目標(biāo)函數(shù)值ftotal。然后，利用式(5)對Agent的屬性值進(jìn)行調(diào)整，權(quán)重越大的屬性值被調(diào)整的概率越小，計算調(diào)整后的目標(biāo)函數(shù)值與調(diào)整前相比取最優(yōu)。

(5)

式中：φi∈(0,1)為屬性調(diào)整系數(shù)，第i個屬性權(quán)重越大則φi越小，根據(jù)實(shí)際問題規(guī)模取值，若實(shí)際問題規(guī)模較大則φi取值較大可以加速收斂。

在引領(lǐng)蜂選擇的基礎(chǔ)上，X個跟隨蜂利用式(6)在rN個位置中選擇蜜源。跟隨蜂選定所在位置后，利用式(7)進(jìn)行屬性調(diào)整，選擇調(diào)整后的最優(yōu)位置為跟隨蜂的位置，并記錄當(dāng)前最好解。

(7)

遍歷所有蜜源，當(dāng)一個蜜源效用值在Nlimit代內(nèi)沒有變化，當(dāng)前位置的跟隨蜂變?yōu)閭刹榉洹ふ覐奈幢贿x擇過的蜜源x，利用式(8)進(jìn)行試探性匹配，若f1>0則當(dāng)前位置被蜜源x替換；如果所有蜜源都被選擇過，則隨機(jī)挑選一個蜜源k利用式(9)進(jìn)行試探性交換匹配，若f2>0則當(dāng)前位置被蜜源k替換。

(8)

(9)

式中：k=rand(0,1)×2N。

最后，計算當(dāng)前目標(biāo)函數(shù)ftotal值是否達(dá)到要求，達(dá)到要求則輸出結(jié)果，否則算法繼續(xù)。

圖1為整個自動談判模型的建模計算過程。

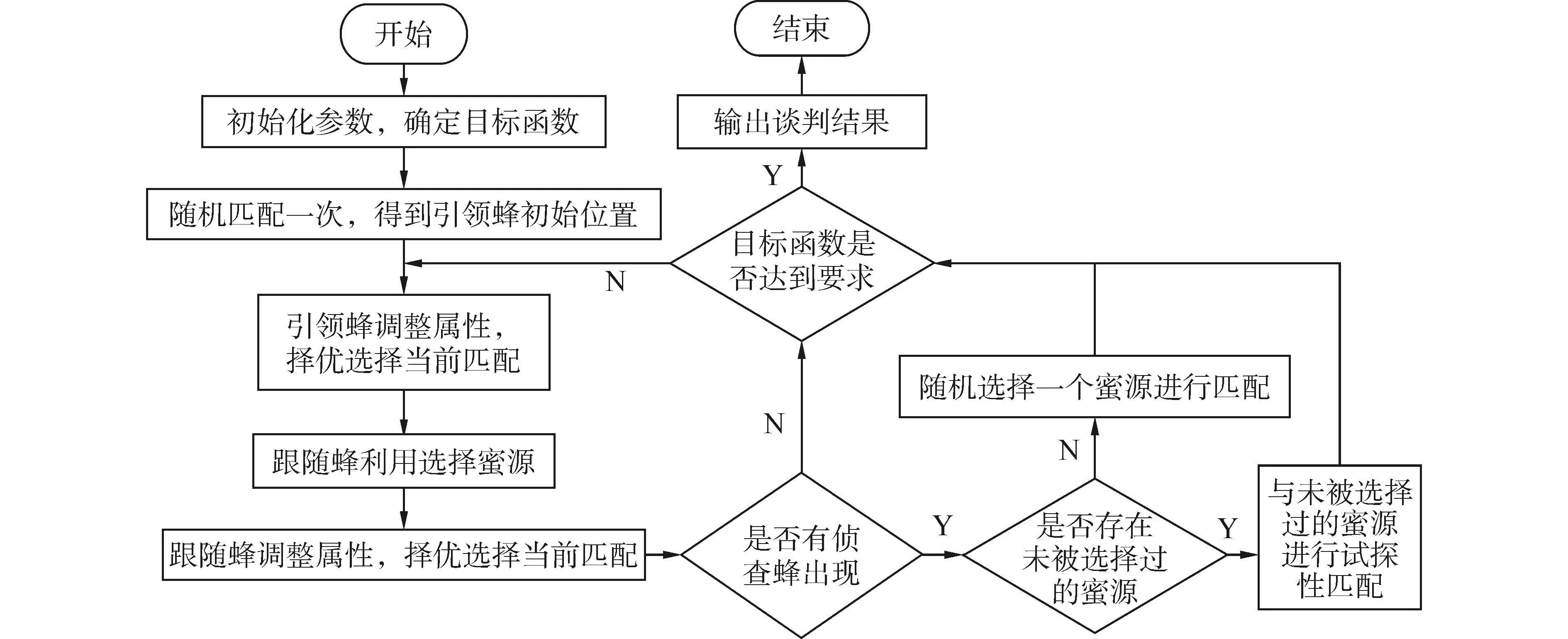
圖1　建模計算流程 Fig. 1　The modeling flow chart

3模型驗證

企業(yè)A、B、C分別需要采購一種工業(yè)原材料，3家企業(yè)對原材料的運(yùn)輸(Delivery)、質(zhì)量(Quality)、價格(Price)分別有各自的要求。3家采購企業(yè)屬性效用值如表1所示，當(dāng)前有4家供應(yīng)商可供選擇，分別為Q、W、E、R，每家供應(yīng)商產(chǎn)品和服務(wù)都各有特色，4家供應(yīng)商的屬性如表2所示。

應(yīng)用本文建模方法，首先從表1和2得到權(quán)重矩陣W、效用值矩陣V和效用調(diào)整范圍{Vmin，Vmax}。主要參數(shù)設(shè)置為屬性最大范圍參數(shù)P=10，蜜源數(shù)量2N=8，引領(lǐng)蜂數(shù)量X=3，屬性數(shù)M=3，r=2。圖2為人工蜂群算法模型求解的計算收斂曲線，從圖中可看出，算法循環(huán)20次后最好解不再變化，平均每次運(yùn)行用時1.843 0 s，整體效用值最大為322.922(保留小數(shù)3位)。此時，需求企業(yè)A選擇供應(yīng)商R，B選擇Q，C選擇W。當(dāng)前所有Agent屬性效用值如表3所示。

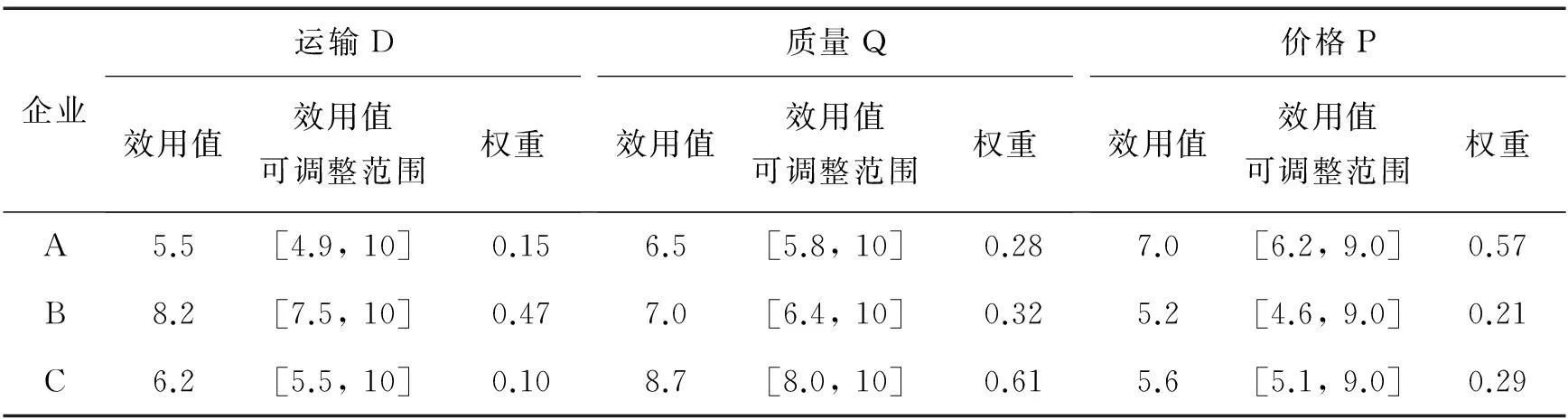
表 1　采購企業(yè)屬性表

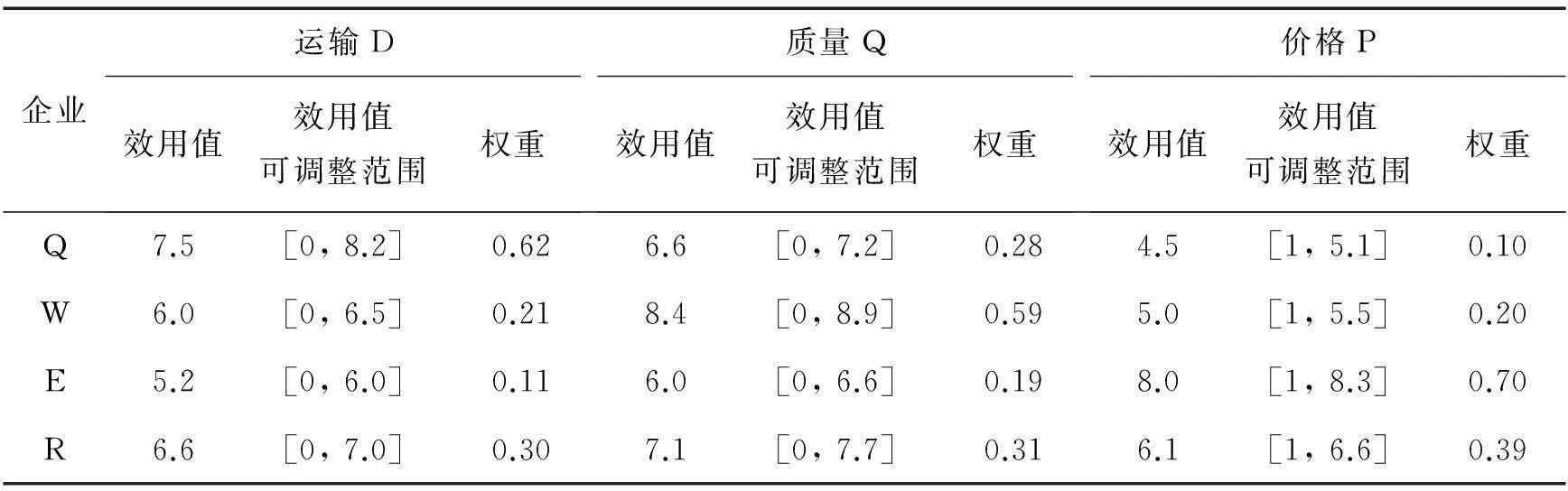
表 2　供應(yīng)商屬性表

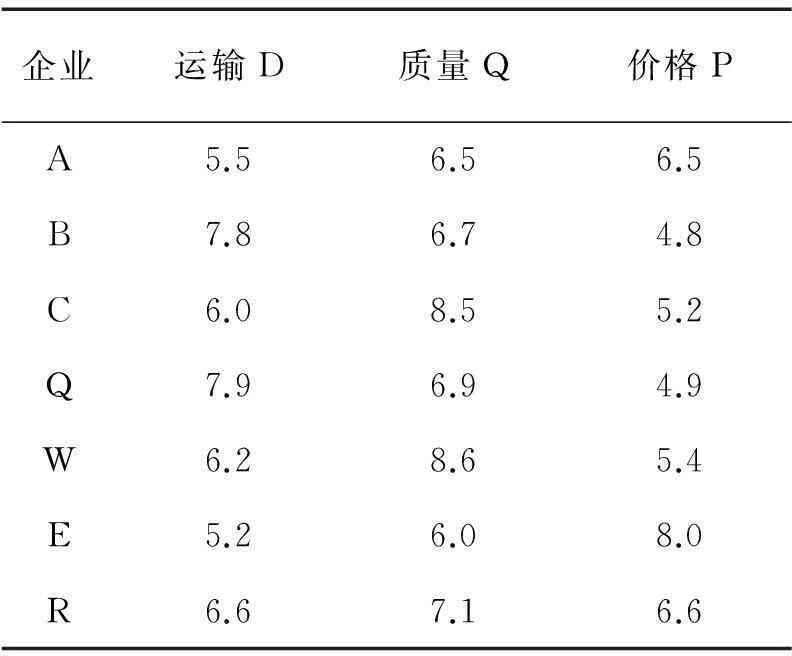
表 3　調(diào)整后效用值

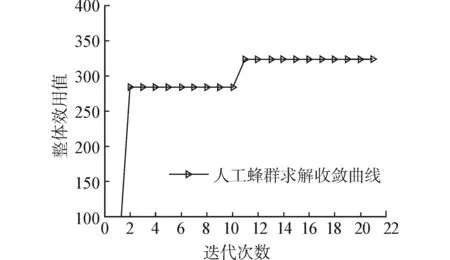
圖2　模型計算收斂曲線 Fig. 2　The convergence curve

文獻(xiàn)[1]給出的多Agent、多Object談判方法(M3INM)中，當(dāng)Object=1時，該模型描述的問題和本文類似。為驗證本文模型的高效性，用文獻(xiàn)[1]中的M3INM模型對本文算例進(jìn)行求解，并與ABC算法的求解結(jié)果進(jìn)行對比。本文模型迭代1次需要1.843 s，循環(huán)20次求得最好解為322.922；M3INM模型迭代1次需3.254 s，循環(huán)20次求得最好解為321.958。本文模型和M3INM模型分別運(yùn)行50次，結(jié)果如表4所示，從表中可看出本文算法計算結(jié)果及求解速度都優(yōu)于文獻(xiàn)[1]。圖3為ABC算法與M3INM模型求解結(jié)果的對比圖，從圖中可以看出，ABC算法求解性能優(yōu)于M3INM，10代以內(nèi)就能收斂到全局最優(yōu)解，M3INM到第20代整體效用值都沒有達(dá)到300。

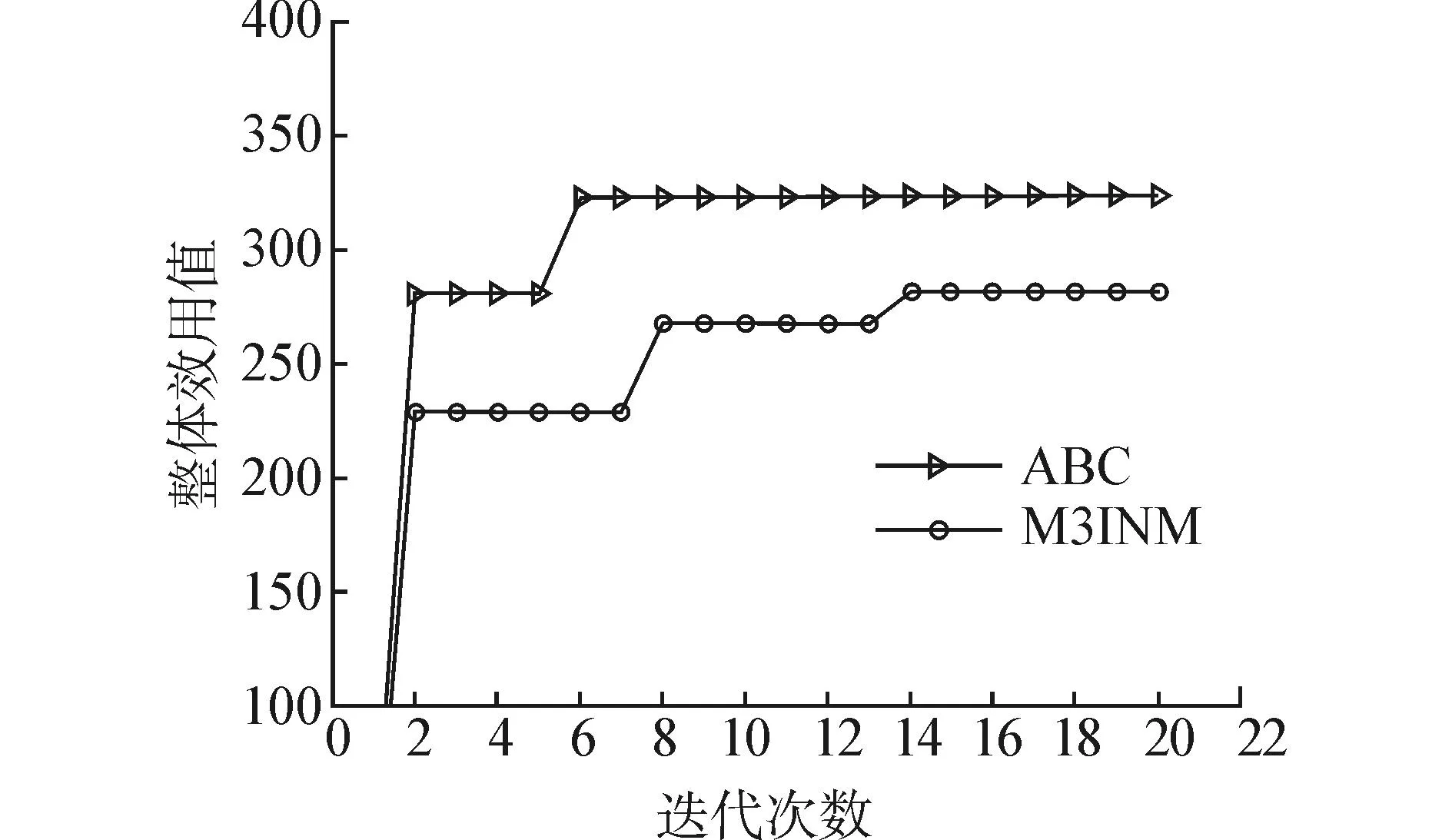
圖3　收斂性對比 Fig. 3　Convergence performance comparison

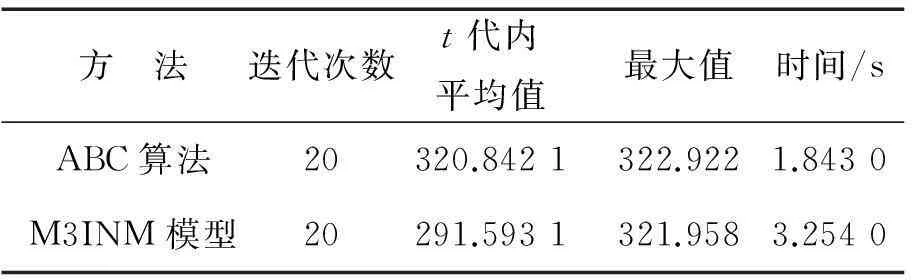
方 法迭代次數(shù)t代內(nèi)平均值最大值時間/sABC算法20320.8421322.9221.8430M3INM模型20291.5931321.9583.2540

4結(jié)束語

本文將人工蜂群算法與多Agent多屬性自動談判模型相結(jié)合，設(shè)計了自動談判模型及求解過程，提供了一種電子商務(wù)自動談判問題的建模求解新思路，具有較強(qiáng)的適用性，能快速找到所有Agent總效用最大的談判結(jié)果。實(shí)例測試結(jié)果及與其他模型的對比，驗證了本文模型的有效性。國內(nèi)外目前對大數(shù)據(jù)量自動談判系統(tǒng)的研究較少，本文后續(xù)研究方向為建立基于人工蜂群算法的一般模型，用于解決大量Agent多屬性談判問題。

參考文獻(xiàn):

[1]FEI Yulian, CHEN Wenjuan. A multi-agent, multi-object and multi-attribute intelligent negotiation model[C]//Fourth International Conference on Fuzzy Systems and Knowledge Discovery. Haikou, China, 2007, 3: 440-446.

[2]黃京華, 馬暉, 趙純均. 面向電子商務(wù)的基本遺傳算法的Agent談判模型[J]. 管理科學(xué)學(xué)報, 2002, 5(6): 17-23.

HUANG Jinghua, MA Jun, ZHAO Chunjun. Multi-agent negotiation model based on genetic algorithm in E-business[J]. Journal of Manegement Sciences in China, 2002, 5(6): 17-23.

[3]ARGONETO P, RENNA P. Production planning, negotiation and coalition integration: A new tool for an innovative e-business model[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(1): 1-12.

[4]CHHETRI M B, LIN J, GOH S K, et al. A coordinated architecture for the agent-based service level agreement negotiation of web service composition[C]//The Australian Software Engineering Conference. Sydney, Australia, 2006: 90-99.

[5]HUANG C C, LIANG W Y, LAI Y H, et al. The agent-based negotiation process for B2C E-commerce[J]. Expert Systems with Applications, 2010, 37(1): 348-359.

[6]高珊, 張惠珍, 馬良. 元胞人工蜂群算法及其在0-1規(guī)劃問題中的應(yīng)用[J]. 數(shù)學(xué)理論與應(yīng)用, 2014, 34(1): 83-91.

GAO Shan, ZHANG Huizhen, MA Liang. Cellular artificial bee colony algorithm and its application to 0-1 programming problems[J]. Mathematical Theory and Applications, 2014, 34(1): 83-91.

[7]REN Z, ANUMBA C J, UGWU O O. The development of a multi-agent system for construction claims negotiation[J]. Advances in Engineering Software, 2003, 34(11/12): 683-696.

[8]孫華梅, 李一軍, 曹榮增, 等. 基于約束放松的電子商務(wù)協(xié)同談判模型[J]. 運(yùn)籌與管理, 2008, 17(4): 132-137.

SUN Huamei, LI Yijun, CAO Rongzeng, et al. Collaborative negotiation model based on relaxative constraints for E-commerce[J]. Operations Research and Management Science, 2008, 17(4): 132-137.

[9]RAHWAN I, KOWALCZYK R, PHAM H H. Intelligent agents for automated one-to-many e-commerce negotiation[J]. Australian Computer Science Communications, 2002, 24(1): 197-204.

[10]BADICA C, GANZHA M, PAPRZYCKI M. Developing a model agent-based e-commerce system[M]//LU Jie, ZHANG Guangquan, RUAN Da. E-service Intelligence. Berlin/Heidelberg: Springer, 2007: 555-578.

[11]王海, 李一軍, 侯新培. 基于Agent的電子商務(wù)自動談判系統(tǒng)研究[J]. 系統(tǒng)工程理論與實(shí)踐, 2005, 25(11): 14-19.

WANG Hai, LI Yijun, HOU Xinpei. E-commerce oriented ANS based on Agent[J]. Systems Engineering—Theory & Practice, 2005, 25(11): 14-19.

[12]高珊, 張惠珍, 馬良. 蜂群算法求解支持模糊QoS約束的電子采購模型[J]. 經(jīng)濟(jì)數(shù)學(xué), 2014, 31(2): 59-63.

GAO Shan, ZHANG Huizhen, MA Liang. Solving E-procurement model based on fuzzy QoS-constraint with bee colony algorithm[J]. Journal of Quantitative Economics, 2014, 31(2): 59-63.

高珊，女，1989年生，碩士研究生，主要研究方向為智能優(yōu)化、系統(tǒng)工程。曾獲美國大學(xué)生數(shù)學(xué)建模競賽二等獎，全國研究生數(shù)學(xué)建模競賽二等獎。發(fā)表學(xué)術(shù)論文6篇。

馬良，男，1964年生，教授，博士生導(dǎo)師，主要研究方向為系統(tǒng)工程、智能優(yōu)化。發(fā)表學(xué)術(shù)論文300余篇，出版專著1部，主編教材2部。

張惠珍，女，1979年生，副教授，博士，主要研究方向為運(yùn)籌學(xué)、智能優(yōu)化。發(fā)表學(xué)術(shù)論文20余篇，出版專著1部。