公交地鐵一體化下的網絡模型與最優路選擇算法

網絡出版地址：http://www.cnki.net/kcms/detail/23.1538.tp.20150526.1415.002.html

公交地鐵一體化下的網絡模型與最優路選擇算法

徐勇，賈欣，王哲，王翠柳

(河北工業大學 理學院，天津 300401)

摘要：公交地鐵網絡出行線路優選問題是公交網絡系統研究的核心問題之一。為此研究了公交地鐵一體化條件下的公交網絡出行優化模型與算法。構造公交地鐵網絡的標號模型及映射網絡模型，以適當倍數縮小地鐵線路上站點之間的權值，進而可將公交與地鐵進行一體化處理，縮小后可使地鐵線路具有明顯的優勢以達到優選地鐵的目的。運用映射網絡圖、二分圖、半張量積等理論給出了公交地鐵一體化網絡的最優路選擇算法。最后實證了該方法在公交地鐵網絡線路優選的有效性。

關鍵詞：公交；地鐵；最優線路；半張量積；標號；映射網絡；二分圖

DOI:10.3969/j.issn.1673-4785.201404036

中圖分類號：TP18; U491 文獻標志碼：A

收稿日期：2014-04-18. 網絡出版日期：2015-05-26.

基金項目：河北省自然科學基金資助項目(A2013202198)；國家大學生創新創業訓練計劃項目(201310080030).

作者簡介：

中文引用格式：徐勇，賈欣，王哲，等. 公交地鐵一體化下的網絡模型與最優路選擇算法[J]. 智能系統學報, 2015, 10(3): 482-487.

英文引用格式：XU Yong, JIA Xin, WANG Zhe, et al. Transit network models and optimal path selection algorithm for the integrated bus and subway system[J]. CAAI Transactions on Intelligent Systems, 2015, 10(3): 482-487.

Transit network models and optimal path selection algorithm

for the integrated bus and subway system

XU Yong, JIA Xin, WANG Zhe, WANG Cuiliu

(School of Science, Hebei University of Technology, Tianjin 300401, China)

Abstract：In this paper, the travel optimal model and algorithm of public transit network for the integrated bus and subway system are studied. First, a label model and mapped network model are constructed for the bus and subway network. The weight between two subway stations is appropriately reduced to deal with the bus and subway integration problem. The subway has obvious advantages after reduction and subway becomes the preferred option. Next, the optimal path selection algorithm of the integration network of bus and subway is given using the mapping network graph, bipartite graph, and semi-tensor product theory. Finally, the effectiveness of the proposed method in optimized selection of the public transit network is illustrated by a numerical example.

Keywords：public transit; subway; optimal path; semi-tensor product; label; mapping network graph; bipartite graph

通信作者：徐勇. E-mail: xuyong@hebut.edu.cn.

日益現代化的交通方式給人們出行帶來很大便利，其中公交與地鐵是大型城市中的主要交通工具。考慮到我國人口眾多，城市交通擁堵問題日益嚴重，對公交地鐵系統的研究已成為一個熱門又困難的課題。公交地鐵系統的研究主要包括網絡構建、公交配流與最優路選擇算法3個方面，而查詢算法在其中起到核心作用，它為人們提供出行的路徑選擇，切身關系到整個公交地鐵網絡是否高效運作，是公交系統研究的核心問題之一。

目前雖然有一系列針對公交網絡的最短路徑搜索算法[1-11]，主要包括基于圖論的查詢算法[1,9]，基于數據庫的查詢算法[2,5]和基于矩陣運算的查詢算法[11]。目前針對地鐵主導下的公交網絡的最短路徑搜索算法卻不多見。

考慮到地鐵在大城市公交系統中日益占主導地位這一事實，在文獻[9]的基礎上，將優選地鐵出行作為基本出發點，對公交與地鐵站點標號的同時，將地鐵線路上站點間的權值成倍縮小，再依次按照換乘次數、乘車距離進行路徑選擇時就達到了優選地鐵的目的，且一體化后的模型更加清晰、簡便。

1高維數組的表示

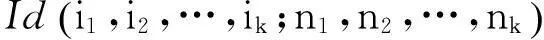
S的大小，即S中元素的個數，記作|S|。且|S|=n1×n2×…×nk。

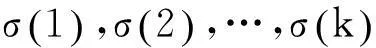
2公交地鐵網絡優化模型

2.1公交地鐵網絡圖

例如，某公交地鐵網絡由1條地鐵線路、2條公交線路、2個地鐵站點(地鐵站點都為公交站點)和2個公交站點(不包含前述地鐵站點)組成，他們分別為地鐵線路L0，公交線路L1、L2，地鐵站點S1、S2，公交站點S3、S4，如圖1。

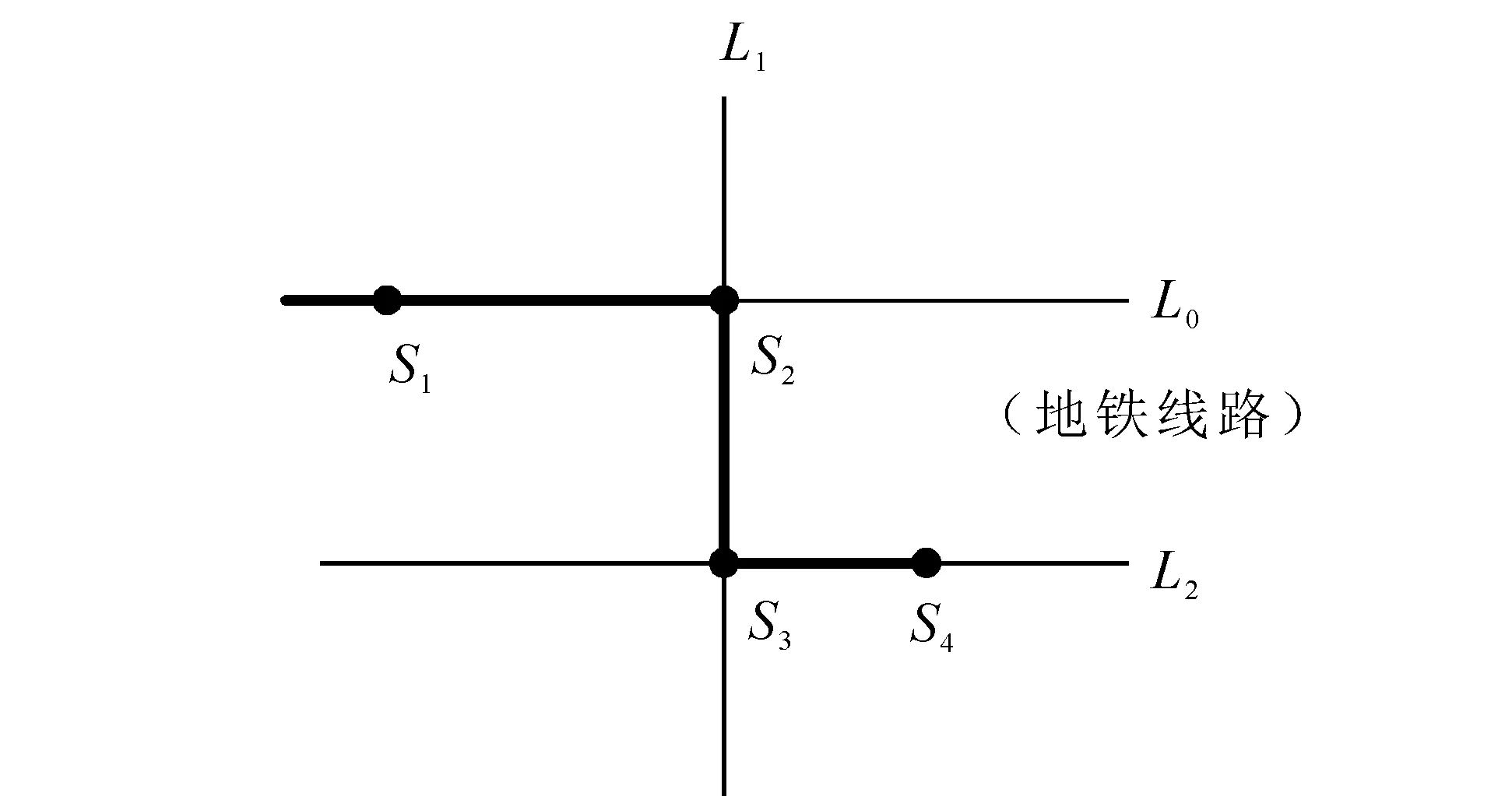
圖1　公交地鐵網絡 Fig. 1　Bus and subway network

2.2公交地鐵網絡的二分圖模型

具有2種屬性的復雜網絡可用二分圖表示[14-15].公交地鐵網絡的站點和線路2種屬性決定了它可以反映到二分圖上。將頂點集合S看作二分圖的上頂點集，線路集合L看作二分圖的下頂點集，公交線路L′經過站點S′，則在L′線路與S′站點之間有邊相連。圖2是圖1的公交網絡對應的網絡二分圖。

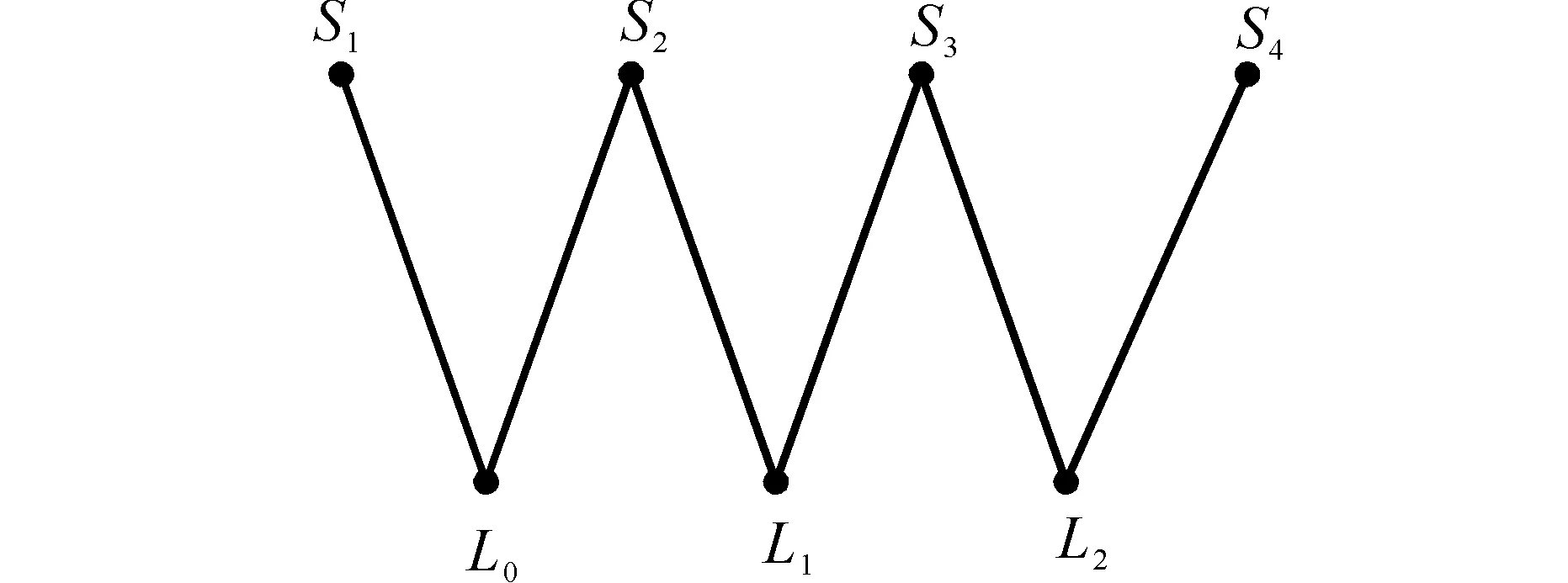
圖2　網絡二分圖 Fig. 2　Bipartite network graph

由圖2看出，S1與S2可直接到達，S1與S3需經過S2轉乘，S1與S4需經過S2,S3轉乘到達。二分圖比網絡圖更加直觀地顯示出換乘次數。

2.3公交地鐵網絡圖的映射圖

公交地鐵網絡圖的映射圖包括線路映射網絡圖和站點映射網絡圖，可以由二分圖得到。

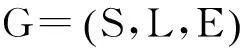
圖3為圖2的線路映射網絡圖，圖4為圖2的站點映射網絡圖。由圖3可以看出，L1與L0、L2之間分別為一條邊，即若出發站點在L1站點上，目的地站點在L0站點或L2站點上，轉乘1次公交或者地鐵即可到達。若出發站點在L0線路上，目的地站點在L2線路上，則需在L1線路上的某2個站點處轉乘，乘坐3次公交或地鐵即可到達目的地。由圖4可以看出，S1與S2有一條邊相連，即兩站點在一條線路上，可以直達。S1與S3之間有2條邊，且經過S2站點，則從S1站點到達S3站點必須在S2站點轉乘，即坐2次公交或地鐵到達。S1與S4之間有3條邊相連，從圖可直接看出，由S1站點出發，需在S2和S3站點轉乘，以到達S4站點。

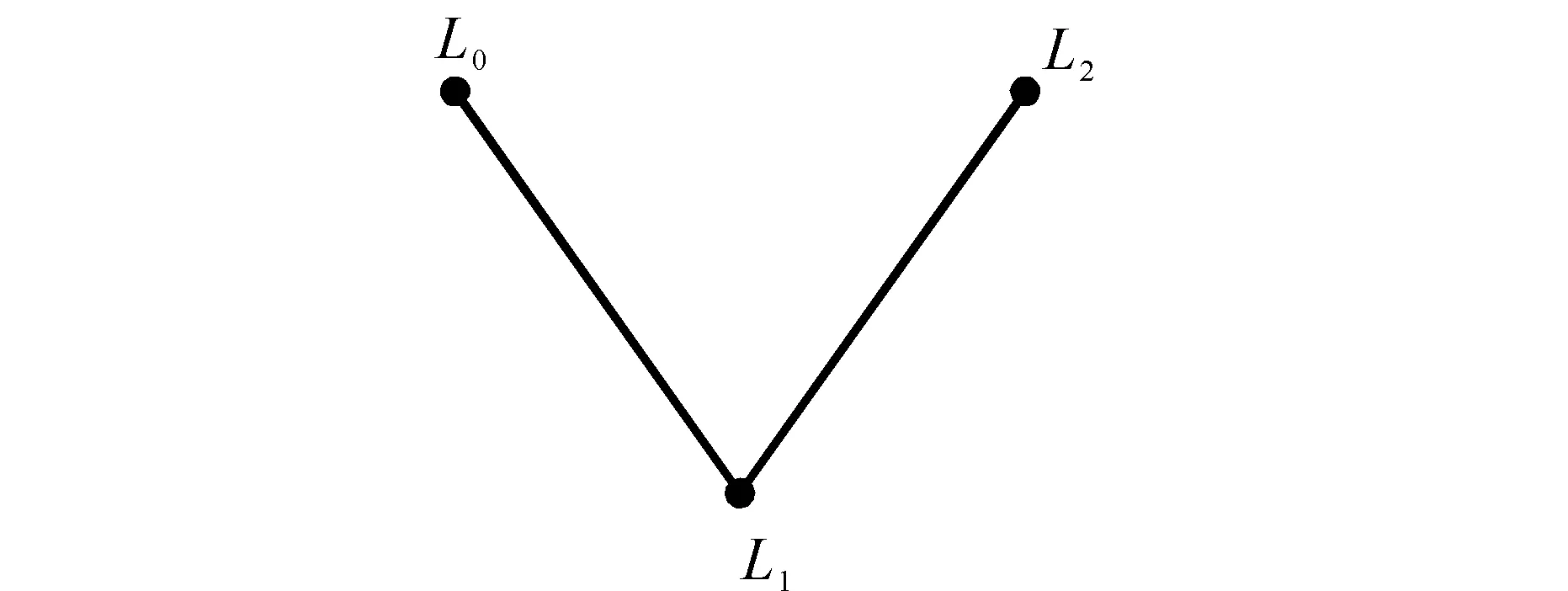
圖3　線路映射網絡圖 Fig. 3　Line mapping network graph

圖4　站點映射網絡圖 Fig. 4　Site mapping network graph

3最優路選擇算法

首先對每條線路上的站點進行一體化標號，考慮到地鐵的快捷性、準時性、舒適性等優點，優選地鐵出行是大勢所趨。這樣，將地鐵線路上兩站點間乘車距離權值適當減小，這樣就達到了優選地鐵出行的目的。

3.1標號公交地鐵網絡的模型

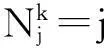
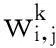
3.2基于標號網絡模型最優路選擇的算法

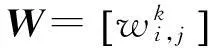
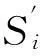
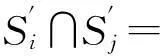
調查表明，在一個成熟的公交地鐵網絡中，2次換乘可以實現絕大多數出發地與目的地之間的連接。

3.3算法的復雜性分析

4算例

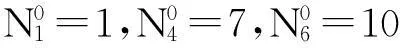
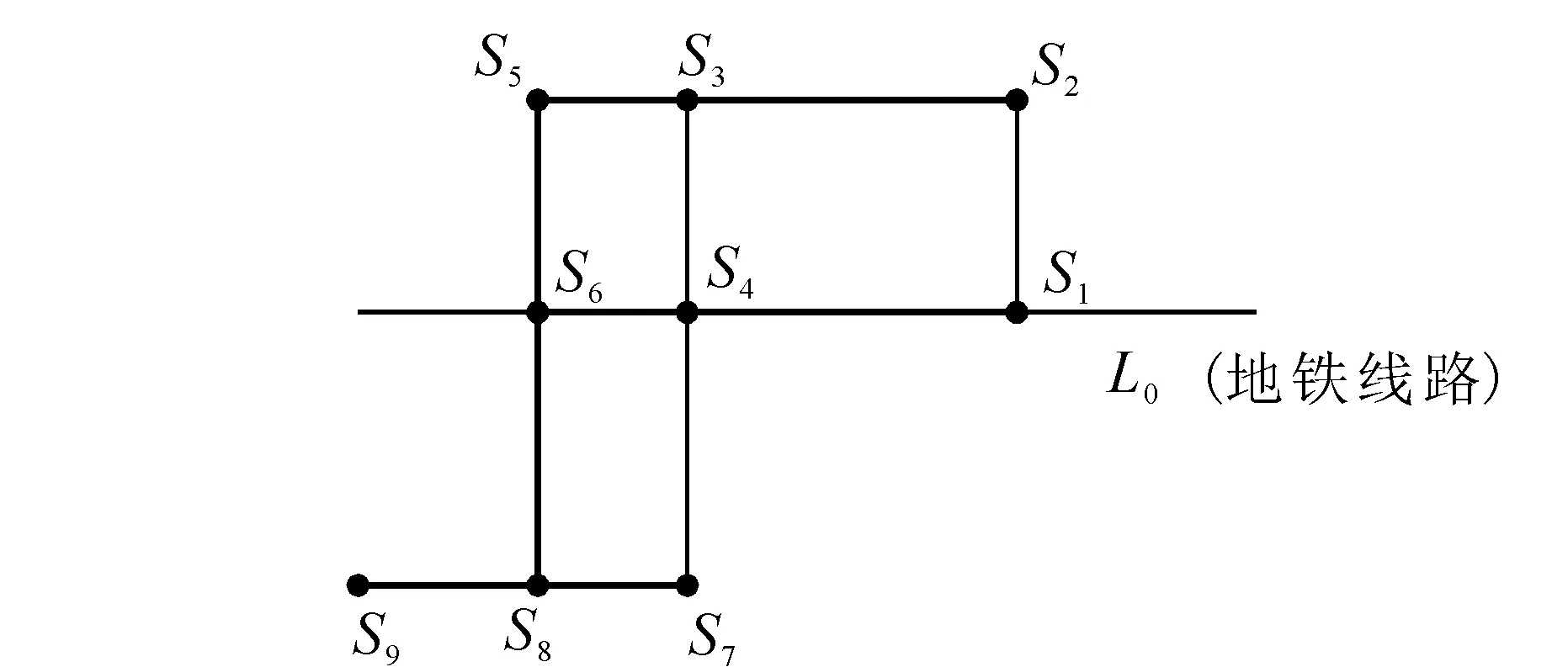
圖5　公交地鐵網絡 Fig. 5　Bus and subway network graph

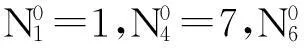
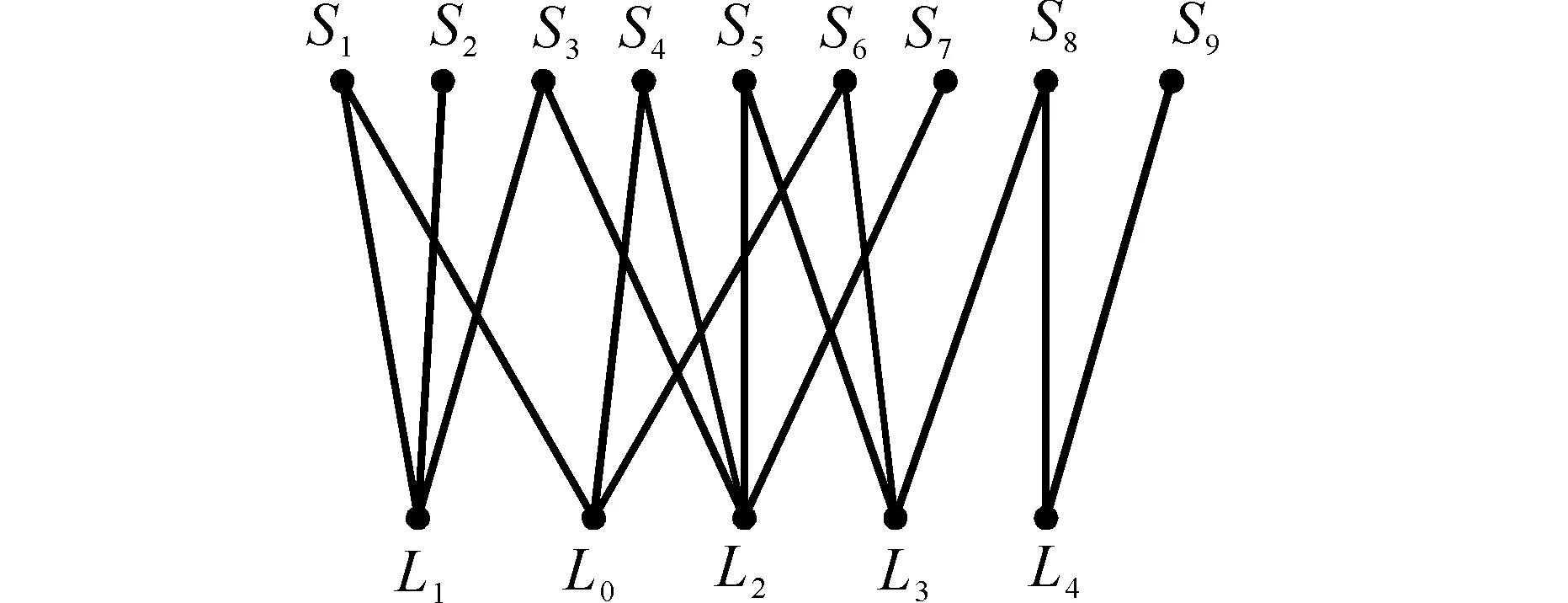
圖6　網絡二分圖 Fig. 6　Bipartite network

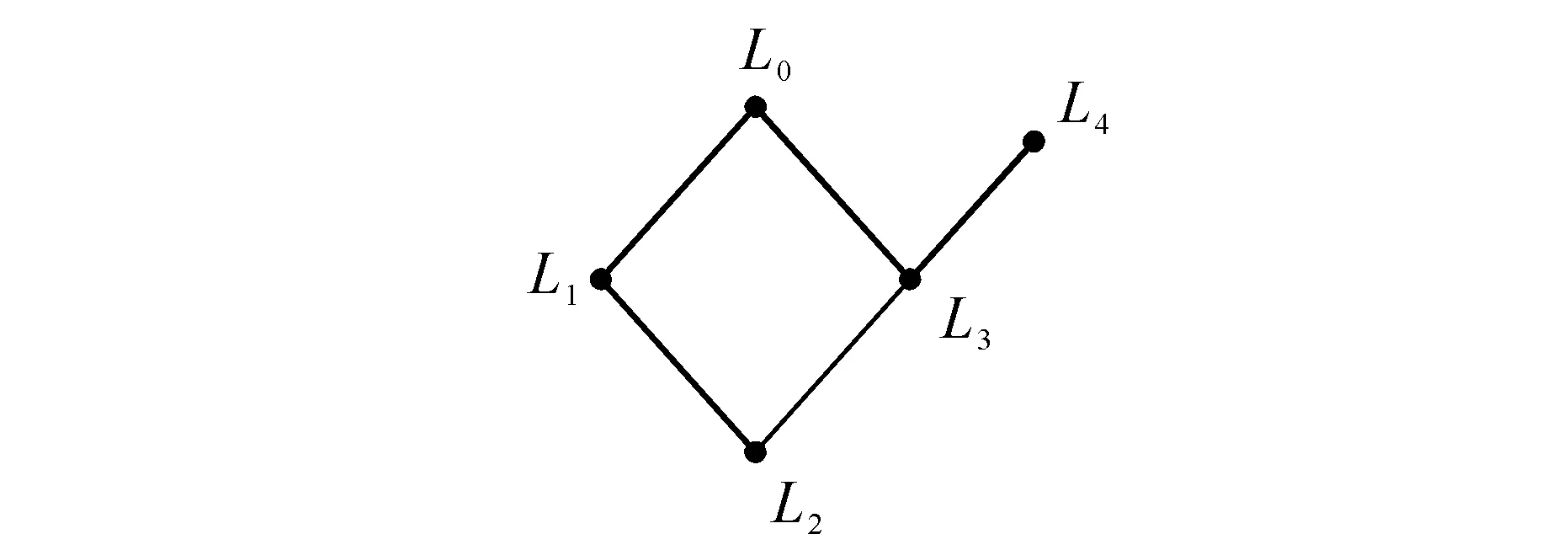
圖7　線路映射網絡圖 Fig. 7　Line mapping network

圖8　站點映射網絡圖 Fig. 8　Site mapping network graph

建立圖5的公交地鐵網絡二分圖，如圖6。圖7為圖6的線路映射網絡圖，圖8為圖6的站點映射網絡圖。

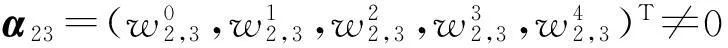
可看出，從S1站點到S5站點與從S2站點到S3站點都是經過6站地，而網絡圖中明顯看出S1,S5站點的距離是遠遠大于S2,S3站點的距離，這是減少地鐵站點標號的權值的結果。結果顯示出地鐵的優越性。

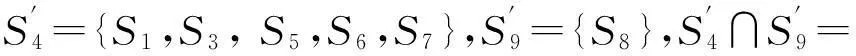
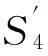
min{6+7+5,1+4+5}=10

對應最優路線為從S4站點乘坐地鐵線路L0到達S6站點，轉乘公交線路L3到達S8站點，再轉乘公交線路L4到達S9站點，途徑10站。

5結束語

在文獻[10]的基礎上，將公交地鐵進行一體化標號，縮小地鐵兩站點間的路徑距離以達到優選地鐵的目的。據乘客出行心理，依次以換乘次數少、出行距離短為優化目標，利用高維數組運算，根據公交地鐵網絡圖與二分圖、線路映射網絡圖、站點映射網絡圖得到兩站點間的最優路徑的選擇算法。

公交網絡的尋徑問題一直以來被認為是NP難問題，而日益發達的公交系統對最優路徑選擇算法的要求也越來越高。因此，改進和創新算法在整個公交系統中至關重要。本文尚未將地鐵的時變性考慮在內，可對此進一步研究，使得人們無論何時出行都有一個對應此時間點的方案，使查詢更加精確可靠。

參考文獻:

[1]閆小勇, 尚艷亮. 基于二部圖模型的公交網絡路徑搜索算法[J]. 計算機工程與應用, 2010, 46(5): 246-248.

YAN Xiaoyong, SHANG Yanliang. Path-finding algorithm of public transport networks based on bipartite graph model[J]. Computer Engineering and Applications, 2010, 46(5): 246-248.

[2]梁虹, 袁小群, 劉蕊. 一種新的公交數據模型與公交查詢系統實現[J]. 計算機工程與應用, 2007, 43(3): 234-238.

LIANG Hong, YUAN Xiaoqun, LIU Rui. Novel model and realization of public transport route inquiring system[J]. Computer Engineering and Applications, 2007, 43(3): 234-238.

[3]王海帥, 冀振燕, 王森. 公交線路查詢算法[J]. 計算機系統應用, 2013, 22(2): 88-91.

WANG Haishuai, JI Zhenyan, WANG Sen. Bus transport transfer algorithm[J]. Computer Systems and Applications, 2013, 22(2): 88-91.

[4]王昉旸, 于麗娜, 鄭保華, 等. “集合燃燒”算法在公交網絡查詢中的應用[J]. 遼寧工程技術大學學報: 社會科學版, 2008, 10(4): 380-382.

WANG Fangyang, YU Lina, ZHENG Baohua, et al. “Aggregate-combustion” arithmetic and its application in the query system of transit network[J]. Journal of Liaoning Technical University: Social Science Edition, 2008, 10(4): 380-382.

[5]伍雁鵬, 彭小奇, 楊恒伏. 改進的基于關系數據庫技術的公交查詢算法[J]. 中南大學學報: 自然科學版, 2009, 40(3): 763-766.

WU Yanpeng, PENG Xiaoqi, YANG Hengfu. Improved algorithm based on relational database technology for querying transit network[J]. Journal of Central South University: Science and Technology, 2009, 40(3): 763-766.

[6]劉健, 徐維祥, 劉旭敏. 公交出行最優路線查詢系統設計[J]. 計算機應用, 2009, 29(S2): 110-112.

LIU Jian, XU Weixiang, LIU Xumin. Design of urban public transit optimal route inquiry system[J]. Journal of Computer Applications, 2009, 29(S2): 110-112.

[7]伍雁鵬, 彭小奇, 黃同成. 基于路徑集合運算的公交網絡尋徑算法研究[J]. 計算機科學, 2009, 36(6): 239-240, 272.

WU Yanpeng, PENG Xiaoqi, HUANG Tongcheng. Research on path set operation based algorithm for path searching in public transit network[J]. Computer Science, 2009, 36(6): 239-240, 272.

[8]劉作虎, 黃明和, 鄒小云, 等. 一種網絡公交查詢系統的改進算法[J]. 計算機與信息技術, 2009, (4): 29-31.

[9]徐勇, 李杰, 張軍芳, 等. 新型公交網絡模型與最優線路選擇算法[J]. 系統工程理論與實踐, 2011, 31(11): 2234-2240.

XU Yong, LI Jie, ZHANG Junfang, et al. New urban transit network models and optimal path searching algorithm[J]. Systems Engineering—Theory and Practice, 2011, 31(11): 2234-2240.

[10]劉旭浩, 徐勇. 基于半張量積理論的公交網絡查詢[J]. 復雜系統與復雜性科學, 2013, 10(1): 38-44.

LIU Xuhao, XU Yong. An inquiry method of transit network based on semi-tensor product[J]. Complex Systems and Complexity Science, 2013, 10(1): 38-44.

[11]張林峰, 范炳全, 呂智林. 公交網絡換乘矩陣的分析與算法[J]. 系統工程, 2003, 21(6): 92-96.

ZHANG Linfeng, FAN Bingquan, Lü Zhilin. Transfer matrix of public transit network and algorithm[J]. Systems Engineering, 2003, 21(6): 92-96.

[12]程代展, 齊洪勝. 矩陣的半張量積理論與應用[M]. 北京: 科學出版社, 2007.

[13]YAO Baozhen, HU Ping, LU Xiaohong, et al. Transit network design based on travel time reliability[J]. Transportation Research, Part C: Emerging Technologies, 2014, 43(3): 233-248.

[14]張譯, 靳雪翔, 張毅, 等. 基于二分圖的城市公交網絡拓撲性質研究[J]. 系統工程理論與實踐, 2007, 27(7): 149-155.

ZHANG Yi, JIN Xuexiang, ZHANG Yi, et al. Topological analysis of urban transit networks using bipartite graph model[J]. Systems Engineering—Theory & Practice, 2007, 27(7): 149-155.

[15]王煒, 楊新苗, 陳學武. 城市公共交通系統規劃方法與管理技術[M]. 北京: 科學出版社, 2002.

徐勇，男，1971年生，教授，博士，主要研究方向為復雜網絡建模與優化。參與或主持省部級科研項目10余項，發表學術論文30余篇，其中被EI檢索10余篇。

賈欣，女，1991年生，主要研究方向為圖論與交通網絡優化。

王哲，男，1990年生，主要研究方向為圖論與交通網絡優化。