二次方分段雙穩系統的隨機共振特性及其應用

二次方分段雙穩系統的隨機共振特性及其應用

張金燕，林敏

(中國計量學院 計量測試工程學院，杭州 310018)

摘要：提出一種二次方分段雙穩勢函數，建立了該勢函數的參數與克萊默斯逃逸率和輸出信噪比的解析關系。并從動力學的角度，分析了不同非線性勢函數下布朗粒子所受的勢場力對增強隨機共振效應的影響。數值仿真與理論分析結論一致。經對軸承滾動體故障數據的分析表明，該勢函數所產生的隨機共振能更有效地實現微弱特征檢測與早期故障診斷。

關鍵詞：隨機共振；二次方分段雙穩勢函數；噪聲助長；軸承故障；微弱信號檢測

中圖分類號:TH113

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.19.034

Abstract:A quadratic segmented bistable potential function was proposed here, the analytic relations among Kramers escape rate, the output signal-to-noise ratio and parameters of the potential function were established. With the principle of dynamics, the influences of the potential field force exerted on Brownian particles under different nonlinear potential functions on enhancing the stochastic resonance produced by the potential functions were analyzed. The results of numerical simulation agree well with the theoretical analysis ones. The analysis of rolling element bearing fault data showed that the stochastic resonance caused by the proposed potential function effectively realizes the weak signal detection and early fault diagnosis.

基金項目：國家自然基金(51304105) 國家自然科學基金(51305209)；江蘇省自然科學基金(BK20130979,BK2011735)；中國博士后科學基金(2013M541678); 江蘇省博士后科學基金(1302052C)

收稿日期：2014-10-22修改稿收到日期：2015-03-05 2014-08-12修改稿收到日期：2015-01-20

Stochastic resonance characteristic of a quadratic segmented bistable system and its application

ZHANGJin-yan,LINMin(College of Metrology and Engineering, China Jiliang University, Hangzhou 310018, China)

Key words:stochastic resonance; quadratic segmented bistable potential function; noise facilitation; bearing fault; weak signal detection

Benzi等[1-2]在研究地球冰川問題時提出了隨機共振，并且將其定義為一種雙穩系統在微弱周期信號和噪聲共同作用下表現出來的非線性現象。隨機共振常用Langevin方程來描述，它涉及微弱周期信號、噪聲以及非線性系統三個基本要素[3]，多用輸出信噪比和功率譜來衡量其效應[4]。在非線性系統中，噪聲的存在可以助長系統中的微弱信號[5]，并且在特定的噪聲強度下系統的輸出信噪比和功率譜能夠達到極大。這使隨機共振在微弱信號檢測領域具有潛在的應用價值[6]。

近年來，人們圍繞著經典雙穩勢函數所產生的隨機共振現象進行了廣泛而深入的研究，通過調節勢函數的參數來產生隨機共振或增強隨機共振效應[7-8]，但經典雙穩勢函數確定的勢能與位移是四次方的函數關系，存在著飽和特性。王澤林等[9-13]提出了分段線性雙穩勢函數和分段混合雙穩勢函數，這些勢函數能避免輸出的飽和特性，且在特定噪聲強度下具有較好的輸出信噪比，能有效地增強隨機共振效應。因此，隨機共振效應與勢函數的具體非線性形式有關，通過選擇不同非線性的勢函數并調節相關參數，能有效地增強隨機共振效應。

線性是互不相干的獨立關系、是唯一的，而非線性則是相互作用的，是多種多樣的。本文研究噪聲與系統非線性的相互作用關系，提出二次方分段雙穩勢函數，建立勢函數的參數與克萊默斯逃逸率和輸出信噪比的關系；并從動力學的角度，分析不同非線性勢函數所確定的常數力、線性力等勢場力對增強隨機共振效應的影響。最后，采用二次方分段雙穩勢函數所產生的隨機共振應用于軸承滾動體的早期故障診斷。

1二次方分段雙穩勢函數

隨機共振的常用動力學方程如下所示：

(1)

式中的微弱周期信號Acos(2πf0t)是外界提供的一個周期性驅動力，f0是周期信號的頻率，幅值A?1；滿足〈η(t)〉=0，〈η(t)η(t′)〉=2Dδ(t-t′)的高斯白噪聲η(t)是粒子受到的一個隨機力，D為噪聲強度。U(x)是系統的勢函數，刻畫了粒子在所處勢場中勢能隨位移的變化，-dU(x)/dx是布朗粒子在勢場中受到的勢場力。改變勢函數U(x)的非線性形式，使微弱周期信號及噪聲之間存在著匹配關系,則能產生隨機共振或者增強隨機共振效應。

經典雙穩勢函數為：

(2)

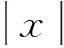
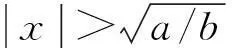
(3)

在相同噪聲強度下，分段混合雙穩勢函數所產生的隨機共振具有更高的輸出信噪比。

分段混合雙穩勢函數將勢能與位移之間原有的四次方函數關系轉變成了線性關系，也將勢場力從非線性力變成了常數力。由于勢函數非線性是多種多樣的，為了尋找隨機共振效應更好的非線性勢函數，本文在x4項與x項之間構建了一個x2項的邊界函數，提出了一種二次方分段雙穩勢函數，從而確定了勢能與位移的二次方函數關系，也確定了勢場力是線性力，其表達式為：

(4)

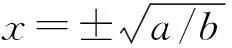
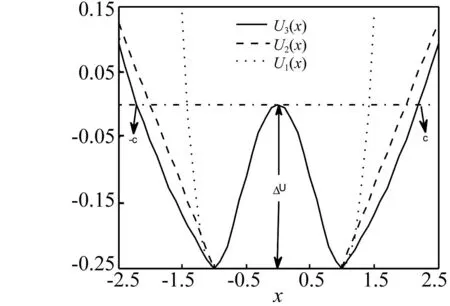
圖1　勢函數曲線 Fig.1 The potential function

不同非線性的勢函數確定了布朗粒子在勢場中將受到不同的勢場力。當參數a=1，b=1時，布朗粒子所受的勢場力隨位移變化的曲線見圖2，其中橫坐標是布朗粒子在勢阱中的位移，縱坐標是布朗粒子所受的勢場力。

從圖2可知，隨著勢函數非線性形式的變化，布朗粒子所受的勢場力也隨之改變。當勢函數為U1(x)時，布朗粒子所受的勢場力為非線性力；當勢函數為U2(x)時，布朗粒子在兩勢阱底之間所受的勢場力為非線性力，在兩勢阱底外側所受的勢場力為常數力且在兩勢阱底處勢場力均存在跳變；當勢函數為U3(x)時，布朗粒子在兩勢阱底之間所受的勢場力為非線性力，在兩勢阱底外側所受的勢場力為線性力且在兩勢阱底處勢場力均存在跳變。因此，選擇不同非線性形式的勢函數，可以改變布朗粒子受到的勢場力，從而影響隨機共振效應。

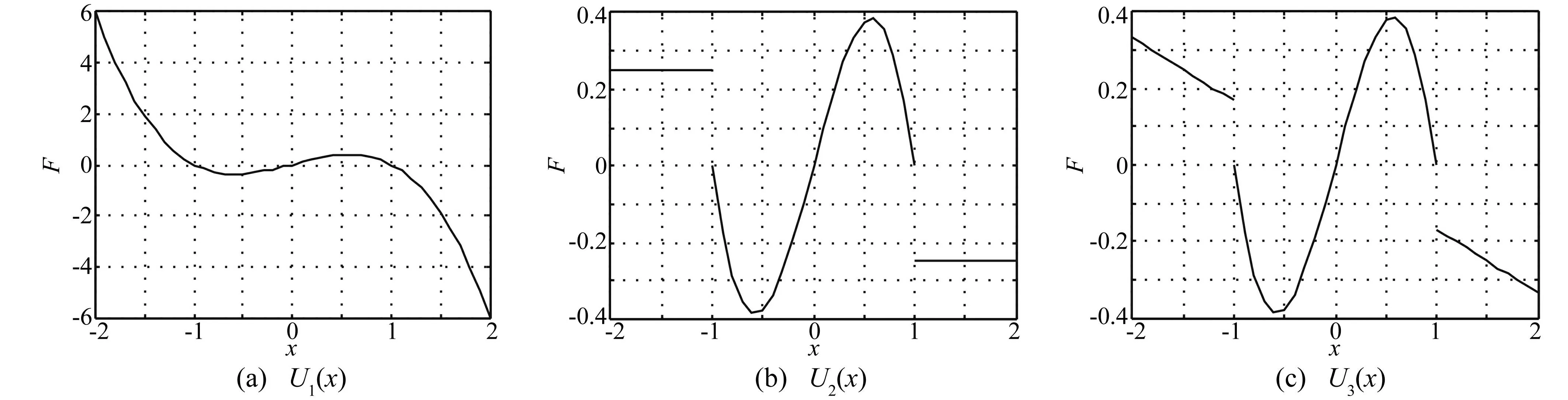
圖2　勢場力變化曲線 Fig.2 The change of potential well Force

1.1特性分析

雙穩系統的Kramers逃逸率可表述為：

(5)

Kramers逃逸率表示布朗粒子在噪聲作用下從一個勢阱躍遷到另一個勢阱的速率，值越大表示布朗粒子在一定時間內躍遷的次數越多，每次耗時越短。由式(5)可知，通過選擇不同非線性形式的U(x)可以改變系統的Kramers逃逸率，從而影響系統對微弱周期信號的響應速率。

將式(4)的U3(x)代入式(5)并取積分，可得：

(6)

進一步簡化得：

(7)

同理

(8)

因此，二次方分段雙穩系統的Kramers逃逸率為：

(9)

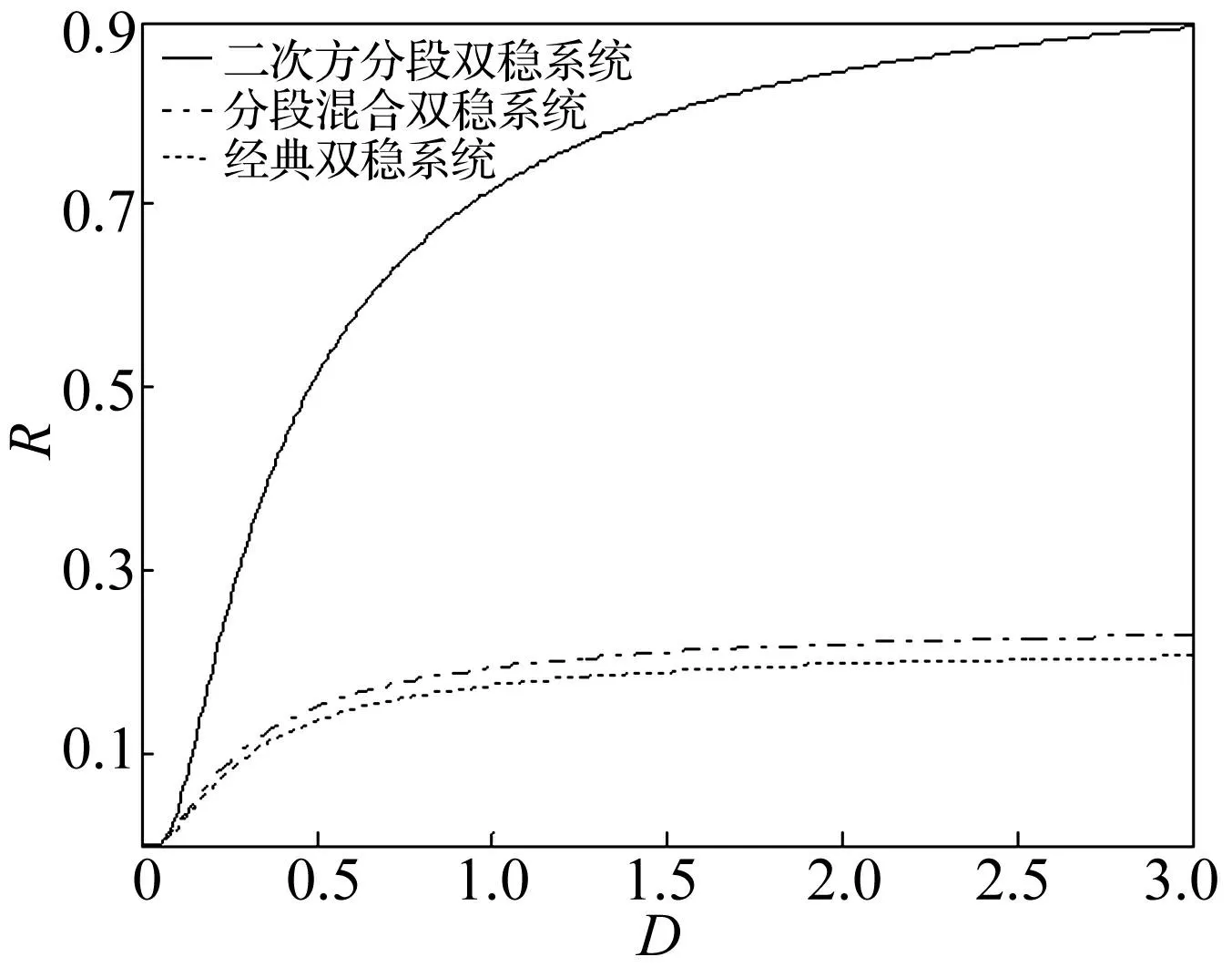
圖3　Kramers逃逸率隨噪聲強度D的變化 Fig.3 The R along with the change of noise intensity D

圖3為當參數a=1，b=1，c=2時，不同非線性的勢函數下系統的Kramers逃逸率隨噪聲強度變化曲線。由圖3可知，Kramers逃逸率會隨著勢函數非線性形式的變化而變化。且在同一噪聲強度下，二次方分段雙穩系統的Kramers逃逸率遠大于分段雙穩系統的Kramers逃逸率。因此，不同非線性的勢函數U(x)能夠影響系統的Kramers逃逸率。

通常采用輸出信號信噪比SNR來衡量系統的隨機共振效應，其定義為噪聲功率與輸出信號功率的比值。系統的輸出信噪比可描述為[14]：

(10)

將式(9)的Kramers逃逸率代入式(10)，可得：

(11)

圖4為當a=1，b=1，c=2，信號幅值A=0.4時，系統的輸出信噪比隨噪聲強度變化的曲線。隨著噪聲強度的變化，系統的輸出信噪比呈現出明顯的單峰曲線，二次方分段雙穩系統的輸出信噪比峰值最大，且峰值點對應的噪聲強度也提高了。因此，勢函數非線性形式的變化能夠影響系統對噪聲的適應性，選擇合適的勢函數形式能達到增強系統隨機共振效應的目的。

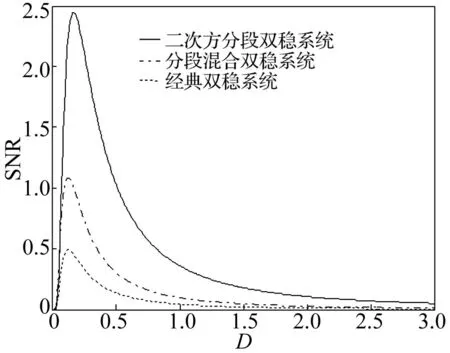
圖4　輸出信噪比隨噪聲強度D的變化 Fig.4 The output SNR along with the change of noise intensity D

2數值仿真結果分析

數值仿真采用四階龍格庫塔算法，系統參數固定為a=1，b=1，c=2，設置采樣頻率fs=5Hz，外界微弱周期信號的頻率f0=0.01Hz，幅值A=0.4。輸入信號為外界微弱周期信號和噪聲的混合信號。當噪聲強度D=0～3時，系統的輸出信噪比變化見圖5。圖5中橫坐標是系統輸入的噪聲強度，縱坐標是系統的輸出信噪比。隨著噪聲強度的變化，系統的輸出信噪比呈現明顯的單峰曲線，二次方分段雙穩系統的輸出信噪比達到了50.7，且峰值點對應的噪聲強度也得到相應提高。因此，二次方分段雙穩系統的輸出信噪比得到了顯著的提高，且對噪聲具有較好的適應性。數值仿真結果與理論分析基本一致。

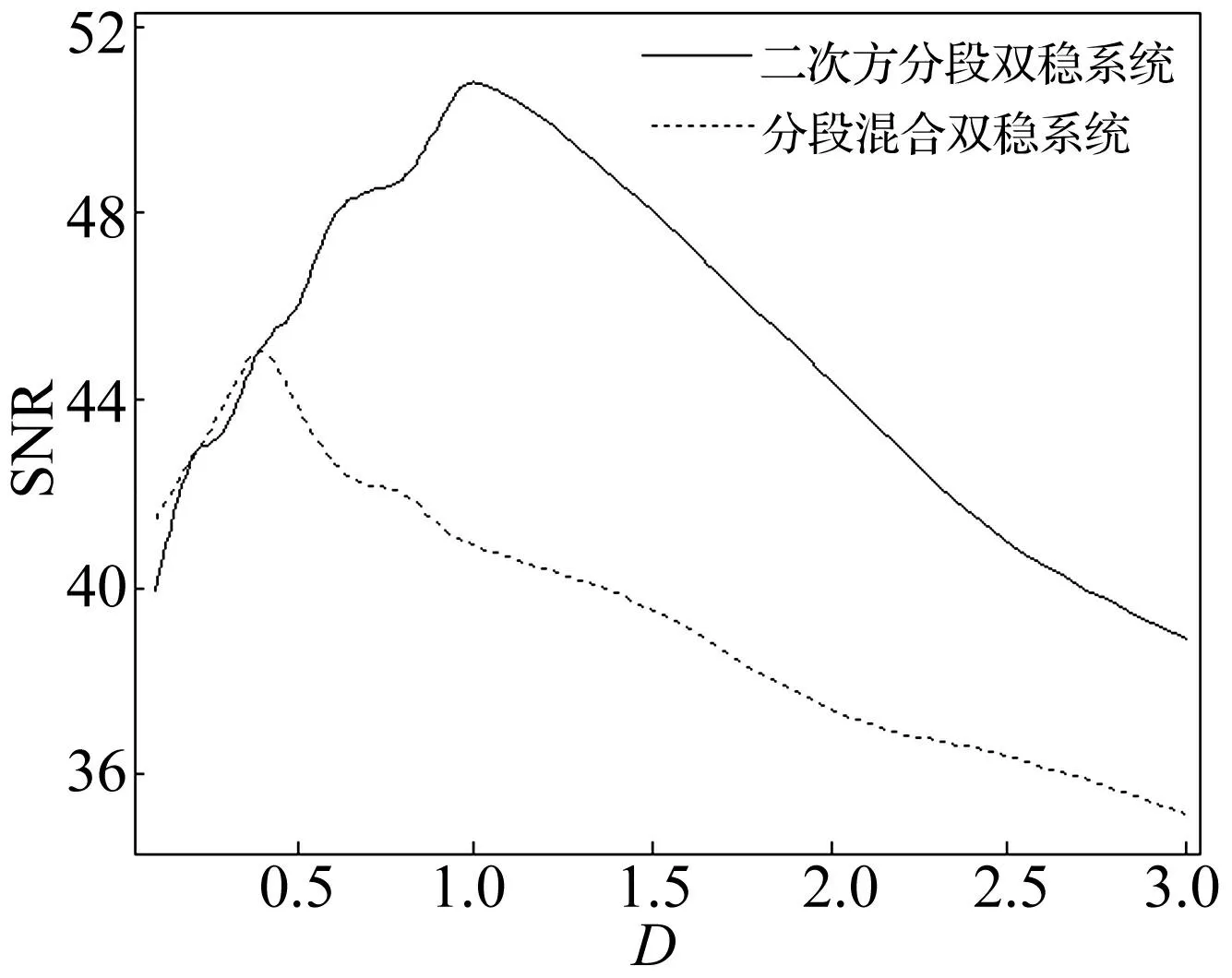
圖5　輸出信噪比的變化 Fig.5 The change of the output SNR

輸入信號s(t)是幅值A=0.4的周期信號與D=0.4的高斯白噪聲的混合信號。圖6為s(t)經過分段混合雙穩系統作用后得到的輸出信號x(t)的時域圖和功率譜圖。圖6表明，待測微弱周期信號頻率f0=0.01Hz處的功率譜值較小。圖7是s(t)經過二次方分段雙穩系統作用后得到的輸出信號x(t)的時域圖和功率譜圖。圖7表明，待測微弱周期信號在頻率f0=0.01Hz處的功率譜值具有顯著提高，譜值達到了0.5749 unit2/Hz。數值仿真結果表明，二次方分段雙穩勢函數能有效增強系統的隨機共振效應。

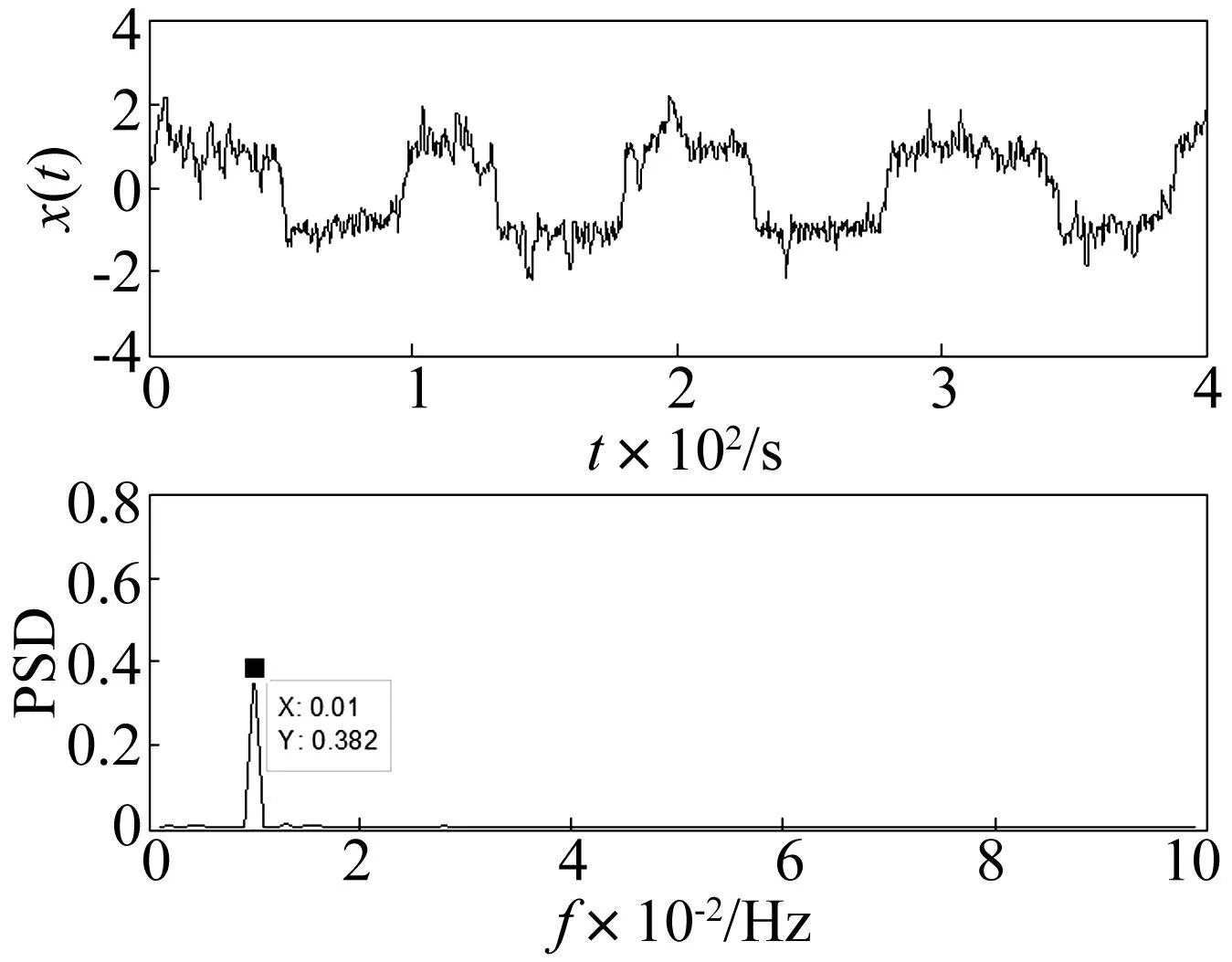
圖6　分段混合雙穩系統的輸出時域圖及功率譜圖 Fig.6 Time-domin waveform and power spectrum of the piecewise hybrid bistable system’s output

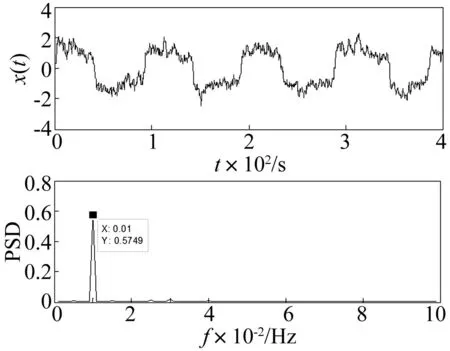
圖7　二次方分段雙穩系統的輸出時域圖及功率譜圖 Fig.7 Time-domin waveform and power spectrum of the quadratic piecewise bistable system’s output

3軸承故障信號檢測結果與分析

滾動軸承是現代工業中常見的機械零件之一。其承受的載荷隨時間變化，在線使用的時間也較長，因此軸承是機械設備中最容易損壞的元件之一。據統計，在使用滾動軸承的旋轉機械中，大約有30%的機械故障都是由軸承引起的[15]。故障的發生勢必會帶來機械生產的不便以及一定的經濟損失，由于故障的產生和形成是一個漸進的過程，因此軸承的早期故障診斷十分必要。

本文選取型號為N/NU 205EM的軸承滾動體故障進行檢測。該軸承的滾動體直徑BD=7.5mm，滾道節徑PD=65mm，內徑Ra=25mm，外徑Rb=52mm，滾動體個數N=12，接觸角β=0°。實驗采集軸承的加速度信號時，設置采樣頻率fs=80kHz，采樣點數N=220=1048576，軸承轉頻f0=25Hz。

隨機共振理論要求輸入信號需要滿足小參數條件，因此對于實測的軸承滾動體故障信號先通過二次采樣進行預處理[16]，設置采樣壓縮比R=5000使其滿足產生隨機共振的小參數條件，再利用二次方分段雙穩系統隨機共振的方法提取微弱特征，最后進行尺度還原后得到對應的特征頻率。選取a=1，b=1，c=2為系統參數。圖8是軸承原始故障信號s(t)的時域圖及功率譜圖，該軸承滾動體待測的周期故障信號完全淹沒于噪聲中，功率譜圖中無法分辨出任何特征故障頻率。

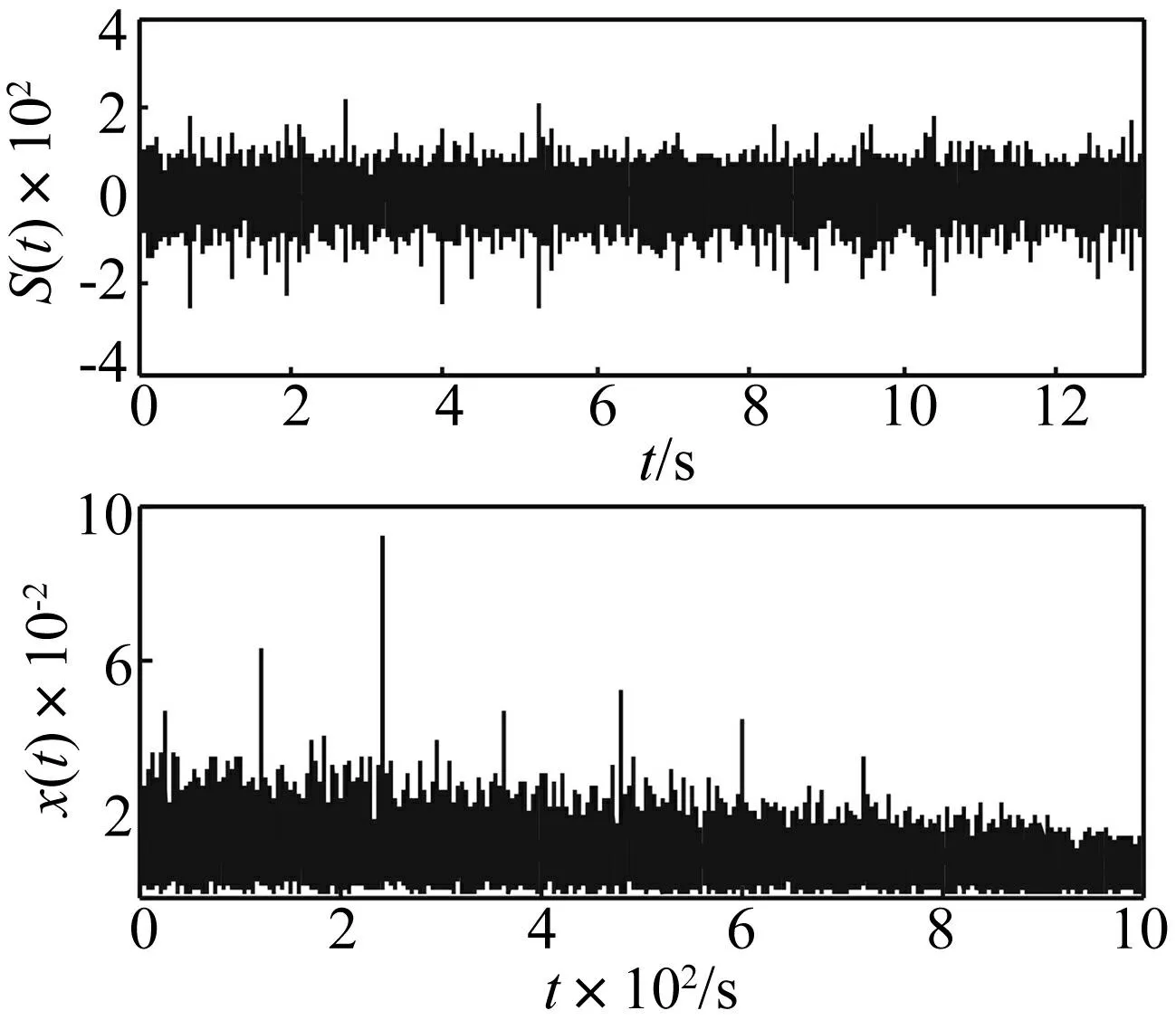
圖8　原始故障信號時域波形圖及功率譜圖 Fig.8 Time-domin waveform and power spectrum of the original bearing falut signal

將含有故障特征頻率的混合信號分別通過分段混合雙穩系統、二次方分段雙穩系統隨機共振作用后，得到系統的輸出功率譜圖見圖9。圖9(a)為分段混合雙穩系統隨機共振后系統的輸出功率譜，其特征故障頻率處對應的功率譜值p(f)=0.09287unit2/Hz，右側仍存在較高的譜值，無法從中分辨出特征故障頻率。圖9(b)是二次方分段雙穩系統的輸出功率譜值，在特征頻率fs=0.2502Hz處存在一個較為突出的譜峰值，相應的功率譜值p(f)=0.1552unit2/Hz。根據頻率壓縮比進行尺度還原，該軸承滾動體對應的故障頻率應為fd=fs·R=125.1Hz。當軸承轉頻f0=25Hz時，滾動體故障頻率的理論值為125.18Hz。圖9(a)與圖9(b)表明，二次方分段雙穩系統隨機共振具有明顯的譜峰值，其譜峰值增加了67.2%。檢測結果可以表明，二次方分段雙穩系統的輸出性能顯著優于分段混合雙穩系統的輸出性能，該方法能夠檢測出軸承滾動體故障。

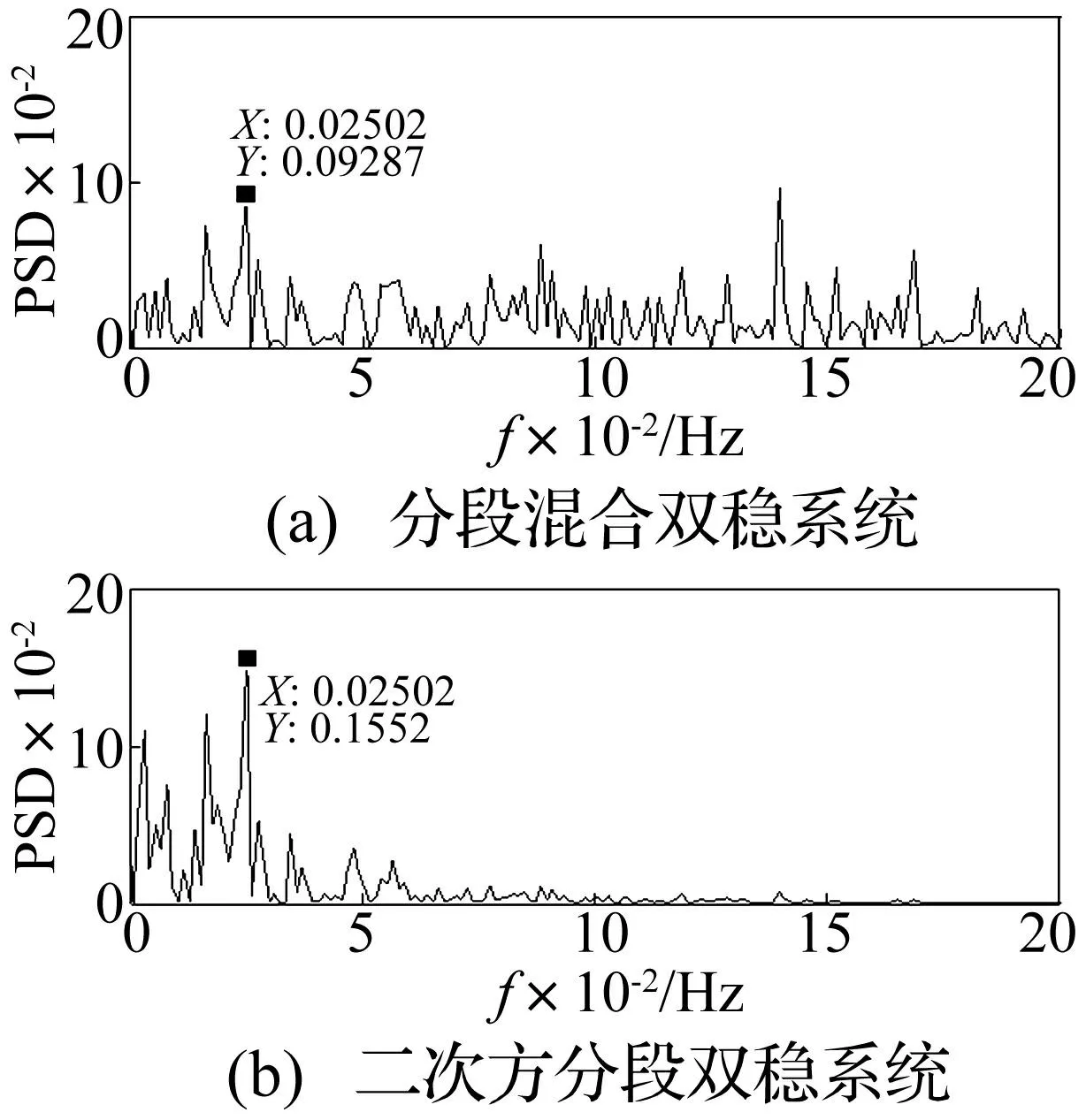
圖9　分段混合雙穩系統和二次方分段雙穩系統輸出功率譜圖 Fig.9 Power spectrum of the piecewise hybrid bistable system’s output and quadratic piecewise bistable system’s output

4結論

隨機共振效應與勢函數的具體非線性形式有關。本文建立了二次方分段雙穩勢函數的參數與系統克萊默斯逃逸率和輸出信噪比的解析關系。并從動力學的角度，分析了勢函數的具體非線性形式對隨機共振效應的影響，揭示了增強隨機共振效應的物理本質。結果表明，二次方分段雙穩系統中，由于布朗粒子受到的勢場力中存在線性力，噪聲的助長作用明顯，整個系統具有良好的輸出信噪比及功率譜。數值仿真結果與理論分析結論完全吻合，且軸承滾動體故障數據的分析表明，該勢函數所產生的隨機共振在軸承故障信號檢測中的應用是有效的。同時也適用于其他強噪聲背景下的微弱信號檢測，應用前景良好。

參考文獻

[1]Benzi R, Sutera A, Vulpinai A. The mechanism of stochastic resonance [J]. Journal of Physics A: Mathematical and General, 1981, 14(11): 453-457.

[2]Gammaitoni L, H?nggi P, Jung P, et al. Stochastic resonance[J].Reviews of Modern Physics, 1998, 70(1): 223-285.

[3]Hu G, Nicolis C. Periodically forced fokker-planck equation and stochastic resonance [J].Phys. Rev. A. 1990, 42(4): 2030-2041.

[4]Benzi R, Parisi G, Stuera A, et al.A theory of stochastic resonance in climaticchange [J]. SIAM Journal on Applied Mathematics, 1983, 43(3): 565-578.

[5]McDonnell Mark D , Ward Lawrence M. The benefits of noise in neural systems: bridging theory and experiment[J].Nature Reviews Neuroscience , 2011,12(6):415-425.

[6]郝研, 王太勇, 萬劍,等. 基于級聯雙穩隨機共振和多重分形的機械故障診斷方法研究[J]. 振動與沖擊, 2012, 31(8): 181-185

HAO Yan, WANG Tai-yong, WAN Jian, et al. Mechanical fault diagnosis based on cascaded biatable stochastic resonance and multi-fractal [J]. Journal of Vibration and Shock, 2012, 31(8)：181-185.

[7]祝恒江, 李蓉, 溫孝東. 利用隨機共振在強噪聲下提取信息信號[J]. 物理學報, 2003, 52: 2404-2408.

ZHU Heng-jiang, LI Rong, WEN Xiao-dong. Extracting information signal under noise by stochastic resonance[J]. Journal of Physics, 2003, 52: 2404-2408.

[8]林敏, 黃詠梅. 調制與解調用于隨機共振的微弱周期信號檢測[J]. 物理學報, 2006, 55: 3277 3282.

LIN Min, HUANG Yong-mei. Modulation and demodulation for detecting weak periodic signal of stochastic resonance[J]. Journal of Physics, 2006, 55: 3277 3282.

[9]王澤林, 趙文禮, 陳璇. 基于隨機共振原理的分段線性模型的理論分析與實驗研究[J].物理學報, 2012,61(16):1-7.

WANG Lin-ze, ZHAO Wen-li, CHEN Xuan. Theory and experiment research on a piecewise-linear model based on stochastic resonance[J]. Journal of Physics, 2012,61(16):1-7.

[10]Fox R F. Stochastic resonance in a double well[J].Physical Review A, 1989, 39(8):4148-4153.

[11]Repperger D W, Farris K A. Stochastic resonance-a nonlinear control theory interpretation [J]. International Journal of Systems Science, 2010, 41(7):897-907.

[12]張瑩, 王太勇,冷永剛,等. 雙穩隨機共振的信號恢復研究[J].力學學報, 2008, 40(4): 528-534.

ZHANG Yin, WANG Tai-yong, LENG Yong-gang, et al. Study on signal recovery in bistable stochastic resonace[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(4): 528-534.

[13]Rana S, Lahiri S, Jayannavar A M. The role of soft versus hard bistable systems on stochastic resonance using average cycle energy as a quantifier[J]. The European Physical Journal B, 2011, 84:323-329.

[14]Zhao Wen-li,Wang Juan, Wang Lin-ze.The unsaturated bistable stochastic resonance system,2013,23:033117.

[15]朱維娜,林敏. 基于人工魚群算法的軸承故障隨機共振自適應檢測方法[J].振動與沖擊,2014, 33(6): 143-147.

ZHU Wei-na, LIN Min.Bearing fault detection method with adaptivestochastic resonancebased on artificial fish swarm algorithm [J]. Journal of Vibration and Shock, 2014, 33(6):143-147.

[16]冷永剛, 王太勇. 二次采樣用于隨機共振從強噪聲中提取弱信號的數值研究[J]. 物理學報, 2003, 52(10): 2432-2437.

LENG Yong-gang,WANG Tai-yong. Numerical research of twice sam pling stochastic resonance for the detection of aweak signal submergedina heavy noise[J].Journal of Physics, 2003, 52(10): 2432-2437.

第一作者毛君男，教授，博士，1960年生

第一作者朱銀龍男，博士后，講師，1981年生

通信作者周宏平男，教授，博士生導師，1964年生

郵箱：hpzhou@njfu.edu.cn