高速球軸承主軸系統的動力學模型及其優化設計方法

第一作者張亞偉男，博士，1972年生

高速球軸承主軸系統的動力學模型及其優化設計方法

張亞偉1， 金翔1， 李蓓智1， 梁越升2

(1.東華大學機械工程學院，上海201620； 2. 佐治亞理工學院機械工程學院，Georgia30332-0320)

摘要：提出和實現了角接觸球軸承的動剛度計算方法，可以有效地考察軸承預緊力和轉速對軸承動剛度的作用。提出了基于高速軸承動剛度的高速主軸系統動力學模型，以及高速主軸工作性能的綜合優化設計方法。該方法通過綜合考慮軸承動剛度、主軸軸承配置方式、工作轉速受限系數、主軸結構參數、撓性接頭細頸磨削工藝及其對高速主軸的精度要求等，快速解析影響主軸工作性能的重要因素及其耦合關系，準確發現高速主軸系統設計方案中的薄弱環節，并對重要影響因素及其取值進行有效的協調設計，為實現主軸系統高性能目標奠定基礎。

關鍵詞：高速主軸系統；工作性能；角接觸球軸承；動力學模型；計算方法；優化方法

基金項目：國家863計劃項目(2012AA041309);國家重大科技專項(2011ZX04016-041)

收稿日期：2014-08-11修改稿收到日期：2014-10-23

中圖分類號:TH212；TH213.3文獻標志碼：A

Dynamic modelling and optimization design of spindle systems with high-speed ball bearings

ZHANGYa-wei1,JINXiang1,LIBei-zhi1,LIANGYue-sheng2(1. College of Mechanical Engineering, University Donghua, Shanghai 201620, China；2. School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0320, U.S.A)

Abstract:A calculation method for the dynamic rigidity of angular contact ball bearings was put forward and realized. By using the method, the mechanism of how the dynamic rigidity is affected by the preload of bearings and rotation speed was effectively investigated. The dynamic model of a high-speed spindle system was built on the basis of analysing the dynamic rigidity of high-speed bearings, and an integrated optimization design method for the work performance of the high-speed spindle was proposed. In the method, the dynamic rigidity of bearing, spindle bearing configuration, working speed limiting factor, structural parameters of spindle, grinding process for flexible connector necking and demand on accuracy of high-speed spindle were comprehensively considered to analyse quickly the key factors affecting the work performance of spindle and to inspect the coupled relations among these factors. So that, the weakness in the design scheme of high-speed spindle can be accurately identified and the influential key factors and their correspondent values can be effectively determined in a coordinated fashion. The study lays a foundation to realize the design of high performance spindle systems.

Key words:high-speed spindle system; work performance; angular contact ball bearings; dynamic model; .calculation method; optimization method

機床對現代工業發展至關重要。機床性能是根據被加工工件的尺寸精度和表面光潔度進行評估的，而這些加工結果都與機床主軸-軸承系統的動態特性密切相關[1]。隨著高速超高速加工技術的優勢得到越來越廣泛的認可和應用，高速主軸及其常用的高速球軸承的動態特性研究已為越來越多專家學者和技術人員所關注。

很多學者開展了相關基礎研究和軸承或高速電主軸的相關研究基于Hertz[2]接觸理論，建立了包括慣性力在內的用于滾動軸承動力學分析的擬靜力學模型。Harris[3]在Jones的基礎上提出了更完善的軸承計算模型，其中考慮了高速運轉時，滾球的陀螺效應，并建立了經典的Jones & Harris滾動軸承內部動態載荷數值計算模型。Gupta[4]考慮了滾球的運動狀態、受力狀態以及各零件間的相互作用, 提出了滾動軸承受力分析的動力學模型。劉艷華等[5]基于Hertz接觸理論，對軸徑向聯合載荷作用下的高速角接觸球軸承進行了靜剛度計算與分析。王保民等[6]以彈性力學理論、滾動軸承動力學分析理論等為基礎，建立了高速角接觸球軸承動力學方程，考察了預緊力對高速角接觸球軸承動態特性的影響。朱益利等[7]等根據Hertz接觸理論和剛性套圈理論，建立了角接觸滾珠軸承的擬靜力學模型，提出了減少非線性方程和引入迭代步長調節因子的方法，解決了Newton-Raphone迭代法求解非線性方程組存在的不收斂和振蕩問題。陳小安[8]建立了考慮內圈彎曲變形的角接觸球軸承動剛度分析模型，經理論和實驗結果發現，內圈徑向撓度和軸承軸向載荷成正比、與轉速成反比。劉良勇[9]根據彈性力學理論，建立了軸承內環轉速與徑向游隙、保持架和溝道底部應力的關系模型，討論了轉速對軸承工作性能的影響。李純潔等[10]提出了角接觸球軸承動剛度的測試方法，分析了不同預緊力、轉速對角接觸球軸承動剛度的影響，發現預緊力<500 N時，角接觸球軸承動剛度與預緊力正相關。

然而，正如Lin所言，在回顧與總結69篇與主軸-軸承系統設計建模有關的研究論文后，認為未來值得研究和具有前景的課題包括五方面，其中：①大部分文章與高速機加工有關，建議加強高速加工對主軸和軸承動態特性影響的研究；②設計方法論文數量少于動態模型，因此，建議應用經典或現代優化技術進行高速主軸-軸承系統設計等。為此，本文將以高速球軸承為對象，構建角接觸球軸承的動剛度解析模型，提出基于高速軸承工作速度及其精度目標的動剛度優化設計方法，揭示軸承球徑與數量、預緊力和工作速度對軸承剛度的非線性演變規律，通過對上述軸承結構參數、工作參數等的綜合協調，評估和實現高速主軸的目標性能。

1高速角接觸球軸承動剛度解析模型的推導

高速滾動軸承動剛度是制約高性能軸承工作性能的關鍵指標，在這一研究領域，國內外專家學者進行了大量研究，取得了許多重要進步：Jones[11-12]著重研究了滾動體在軸承內的運動方式和滾動體與滾道之間的接觸機制，這以后，Harris 在Jones理論的基礎上提出了更為全面的軸承計算模型，這個模型稱為JH模型，盡管JH在分析軸承動力學某些參數時有良好效果，但是其計算過程太過于復雜；Gargiulo[13]提出了一個用于計算軸承載荷-變形的經驗公式，然而只能應用于計算靜態剛度；Kraus等[14]通過模態測試測量了軸承的剛度和阻尼等參數，認為軸承動剛度與靜剛度非常接近，用靜剛度代替動剛度，顯然結論難以令人信服，特別是高速狀態。本文提出了一種高速角接觸球軸承動剛度解析計算模型，與目前已有的滾動軸承動剛度計算模型相比，本文提出模型的不同之處與創新點在于：①已有的模型大多數采用靜剛度優勢動剛度，使理論計算結果與工程應用有較大偏差，本文提出的模型通過定義與外載荷非直接關聯的位移和接觸變形量為直接變量函數，構建的計算模型反映了高速軸承動剛度狀況，為高速主軸性能優化提供了依據；②JH模型雖然可用于軸承動力學參數計算，但計算過程復雜，且計算涉及相當數量非線性方程組，且參數間有很強的耦合性，影響計算的效果。③本文提出的模型聚焦影響軸承動剛度關鍵要素及其關系，表達簡單直接明確，大大減少了計算量。在外載荷和軸承轉速的共同作用下，軸承滾球與內外環滾道的接觸位置會發生改變。圖1給出了軸承外環被固定的情況下，滾球與內環相對外環滾道的偏移和接觸變形情況，其中:Oi′和Obq′為偏移后的內環滾道曲率中心和滾球中心。Fa、Fcq、Mgq、Qiq、Qoq分別為軸向外載荷、離心力、陀螺力矩，以及內外環滾道對滾球的反作用力。Fa包括預緊力Fpl。δiq和δoq分別為滾球與內外環滾道的接觸變形。αiq、αoq分別為滾球與內外環滾道的接觸角，隨著位置偏移量或變形的增大，軸承的動態內接觸角αiq增大，但動態外接觸角αoq減小。足標q表示第q個滾球。

圖2定義了軸承坐標系和滾球的方位角，其中設z為軸承軸向、x和y為徑向，相應變量統一用足標a和r表示。φq為第q個滾球的方位角，Ri為軸承動態載荷下內環滾道的曲率半徑，Z為軸承滾球數。

設：軸承內環徑向、軸向和旋轉方向上的外部載荷為Fr、Fa、M。根據圖1～圖2，可以建立如式(1)～式(3)所示的力平衡方程式。

圖1　滾球與滾道動態接觸及位置偏移示意圖 Fig.1 Schematic diagram for dynamic contact between ball and raceway and their relative offsets

圖2　軸承坐標系及滾球方位角示意圖 Fig.2 Schematic diagram for ball’s position angle with bearing’s coordinate

(1)

(2)

(3)

(4)

式中：Kiq為Hertz接觸剛度系數，可依據文獻[13]查詢和計算。

圖3給出了內環和滾球偏移和接觸變形后的幾何關系，相關函數關系式如式(5)～式(11)所示。

(5)

(6)

圖3　滾球與內環偏移前后的幾何關系示意圖 Fig.3 Schematic diagram for geometric relationship between ball and inner ring with their offset and without offset

(7)

Ooi′(r)=BDcosα0+δrq

(8)

(9)

(10)

將式(4)～式(6)代入式(1)～式(3)，以建立外載荷與位移或接觸變形的關聯模型，如式(11)～式(13)。

(11)

(12)

(13)

設：Oob′(a)、Oob′(r)、δiq、cosφq、sinφq是δr、δa、δφ的函數，如式(14)所示，代入式(11)～式(13)后形成式(15)～式(17)。

Oob′(a)=fa(δr，δa，δφ)

Oob′(r)=fr(δr，δa，δφ)

δiq=fδi(δr，δa，δφ)

(14)

cosφq=fφc(δr，δa，δφ)

sinφq=fφs(δr，δa，δφ)

(15)

(16)

(17)

BD=ri+ro-D

(18)

對式(15)～式(17)求偏導，以獲得軸承的軸向、徑向和角動剛度，如式(19)～式(21)所示。

Kr=

(19)

Ka=

(20)

Kφ=

(21)

式(19)～式(21)給出了高速角接觸滾動球軸承動態載荷下，計算動剛度的解析方法。該數學模型以轉速和外載荷的作用為前提，與以往的計算模型不同，計算的是動剛度，通過這個數學模型，可以通過解析法對函數求導可以得到軸承的軸向、徑向和角動剛度精確計算值。

2高速主軸工作性能的綜合優化設計方法

任何工序的加工精度及表面質量主要取決于機床主軸系統及進給系統的動態工作性能。機床主軸系統設計涉及工藝目標、主軸轉速、軸承剛度、軸承預緊力、主軸軸承配置方式、工藝載荷等多種要素，這些要素不僅相互作用，而且還具有交錯與分層的耦合作用，從而使主軸系統的優化設計變得極為復雜(見圖4)。為此，以磨削撓性接頭細頸的納米磨床主軸系統設計為對象，討論和提出高速主軸工作性能的綜合優化設計方法。該方法的工作流程：①明確設計目標及技術要求；②高速主軸方案設計；③軸承預選及其動剛度計算；④主軸實際可達工作轉速及最高轉速計算；⑤基于軸承動剛度的高速主軸動力學模型及其計算分析；⑥基于高速主軸相關要素的優化調設計，并給出優選設計結果。

圖4　機床主軸系統設計所涉及的要素及其相互作用圖 Fig.4 Factors and their interaction for design of machine tool’s spindle system

2.1設計目標與技術要求

根據納米磨床整機設計、撓性接頭細頸精度及其表面質量等的綜合要求，主要技術要求如下：砂輪線速度>8 m/s；高速主軸砂輪端部的徑向跳動<0.5 μm；磨削力約3～6 N；納米磨床主軸部件重量不超過10 kg。

綜合主要技術要求，初步確定高速主軸工作轉速應>80 000 r/min；主軸支承軸頸直徑應<18 mm；前后軸承距離應<200 mm；砂輪磨桿直徑為9 mm(據相關品牌產品目錄)。

2.2主軸軸承選型及其動剛度計算

根據以上的設計目標和初選參數，選擇FAG的高速陶瓷球軸承，并確定前端和后端的軸承內徑分別為17 mm和15 mm，型號分別為HCB71903-C-T-P4S和HCB71902-C-T-P4S，滾球數均為15。

如圖2所示，對于不同的徑向載荷，處于每個方位角的滾動體也有不同的實際接觸角，當徑向載荷增大時，內外接觸角的差異開始變得明顯；同時軸承內滾動體的離心力和陀螺力矩的作用使得每一個滾動體都會與內外滾道發生接觸，產生接觸力和接觸變形。

采用所提出的軸承動剛度計算方法及研制的計算模塊，對上述軸承進行動剛度等的計算。計算時不考慮磨削力。本文給出軸承誤差敏感方向，即徑向剛度與軸承轉速和預緊力的演變規律(見圖5)。其中預緊力是FAG推薦的輕中重三檔值。由圖5可知，徑向動剛度與預緊力成正比，該結論與大多數學者的研究成果一致；隨著轉速提高，軸承內滾道與外滾道的實際接觸角的大小差異將逐漸明顯，進入高速旋轉狀態時，主軸軸承滾動體產生的離心力以及陀螺力矩等慣性力會大幅度增加，高速旋轉時，離心力改變了滾動體與滾道之間的接觸機制，外滾道的接觸載荷明顯高于內滾道的接觸載荷，且在軸承剛開始啟動時這樣的變化非常急劇，達到相對高的轉速后趨于平穩。反映在圖5上，剛度表現為重預緊強度下，徑向動剛度與轉速成反比，該結論與大多數學者的研究成果一致，但在輕或中預緊情況下，徑向動剛度先隨轉速上升而下降，當轉速高于50 000 r/min或100 000 r/min后，徑向動剛度呈輕微上升趨勢。

圖5　徑向剛度與軸承轉速和預緊力的演變規律 Fig.5 The rule of among radical stiffness, rotation speed of bearing and preload

2.3主軸實際可達工作轉速及最高轉速的計算

主軸實際可達到的工作速度與主軸系統的總能量平衡情況有關，如軸承數量及其布置方式、內外載荷、潤滑和散熱等。表1為FAG軸承實際工作速度的受限系數。主軸轉速應按式(22) 計算確定。

nR=nW/fn

(22)

式中：nR、nW、fn分別為主軸最高轉速、實際工作轉速和轉速受限系數。

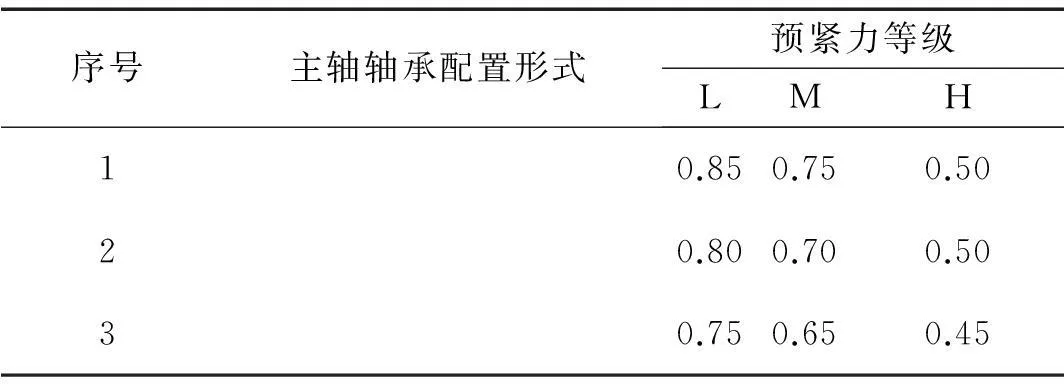
表1　軸承工作轉速的受限系數(f n)

對比考察方案：①表1所示的第1和第2種設計方案，即方案1為主軸系統前后支撐各用一個軸承并背靠背配置；方案2為主軸系統前后支撐各用一對軸承并背靠背配置；②輕或中等預緊強度。將設計目標中初步確定的80 000 r/min主軸轉速，以及方案中最小的主軸工作轉速受限系數0.7代入式(22)，則可確定主軸最高轉速應為120 000 r/min，這樣，方案1的主軸系統實際可達的工作速度分別為102 000 r/min和90 000 r/min；方案2的實際工作速度分別為96 000 r/min和84 000 r/min。

2.4高速主軸動力學模型及其計算分析方法

高速主軸工作精度必須滿足納米磨床的設計目標與技術要求，必須綜合考慮工藝載荷、軸承剛度及其配置方式等的影響，以保證工具，或工件精度和表面質量。為此，構建基于軸承動剛度的高速主軸動力學模型并進行相應的計算與分析。圖6給出了基于軸承動剛度的主軸動力學模型示意圖，工具端部變形的計算模型如式(23)所示。

(23)

式中：δ(wo)、δ(fb)、δ(bb)、δ(sp)分別為工具端部、前主軸、后軸承和主軸的變形。

本設計中，工作精度指標主要是主軸的徑向跳動，即δ(wo)=0.5 μm；因此，必須考察軸承及主軸的徑向載荷和工作剛度。徑向載荷除徑向磨削力外，還應考慮離心力的影響(忽略陀螺力矩，因其引起的徑向分力僅為離心力的1/10～1/11)。即式(23)中的高速磨削環境下的徑向合力應滿足式(24)。

Fr(work)=Fr(proc.l)+Fc

(24)

本設計中：Fr(Proc.l)=10 N，并計算不同工作速度下的離心力，主軸系統在可達速度條件下的工作剛度(見表2)。

表2　主軸實際可達工作速度下的工作剛度

將圖6的相關力學幾何關系代入式(23)，主軸伸出端變形如式(24)所示。

圖6　基于軸承動剛度的主軸動力學模型示意圖 Fig.6 Schematic diagram for the spindle’s dynamic modelling based on the dynamic stiffness of bearing

(25)

2.5基于主軸工作性能的相關要素協調設計方法

相關設計協調要素及其取值如下：磨桿直徑為9～12 mm；主軸伸出長度為30～60 mm(大者為優)；軸承間距為120～240 mm；軸承數為2～4個。經對本設計對比方案進行計算分析后發現，伸出端(磨桿)直徑和長度是控制砂輪端部變形的重要因素。軸承間距與伸出端長度之比幾乎對軸端變形沒有任何影響，即在必要的伸出端長度前提下，縮短軸承間距可實現主軸減重和體積目標。相對軸承剛度，磨桿剛度顯得非常微弱，因此，采用2對軸承相對一對軸承對控制砂輪端變形并不具備很大優勢(見圖7)。

綜上，滿足結構設計要求和δ(work)< 1 μm的最優方案是：磨桿直徑為12 mm、主軸伸出長度為45 mm，并采用2對軸承背靠背配置。此外，由于高線速度更有利于改善表面質量，工程應用中可選用小預緊力(11 N)和高的轉速。

圖7　相關設計要素與砂輪變形的關聯作用 Fig.7 the correlations between the relevant design factors and deform of grinding wheel

3結論

(1)以外環固定的軸承及其滾球為載體，描述了作用軸承內環上的外載荷及其位移或接觸變形的關聯模型，通過定義與外載荷非直接關聯的位移和接觸變形量為直接變量的函數，構建了預測軸承動剛度的偏導數計算模型，并研制了相應的計算機軟件，可以有效地預測高速球軸承的動剛度。

(2)通過計算發現，高速角接觸球軸承的徑向剛度與轉速呈非單調遞減規律。除重預緊外，采用輕或中預緊情況下，徑向動剛度曲線出現拐點，即在拐點之前，徑向剛度隨轉速上升而下降；反之，徑向動剛度隨速度上升而略有提高。輕預緊拐點發生在50%的額定轉速時，中預緊則發生在83%的額定轉速。即采用輕預緊強度，更有利于體現高速軸承的高速與高動態特性。

(3)提出的基于高速軸承動剛度的主軸系統動力學模型，以及高速主軸工作性能的綜合優化設計方法，可以快速解析影響主軸工作性能的重要因素及其耦合關系，準確發現高速主軸系統設計方案中的薄弱環節，并通過對重要影響因素及其取值進行有效的協調設計，實現主軸系統既定的工作性能目標。

參考文獻

[1]Lin C W, Lin Y K, Chu C H. Dynamic models and design of spindle-bearing systems of machine tools: A review[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(3): 513-521.

[2]Jones A B. A general theory for elastically restrained ball and radial roller bearings under arbitrary load and speed conditions[J]. ASME Journal of Basic Engineering, 1960,82: 309-320.

[3]Harris T A, Mindel M H. Rolling element bearing dynamics[J]. Wear, 1973, 23: 311-337.

[4]Gupta P K. Advanced dynamics of rolling elements [M]. New York: Springer, 1984.

[5]劉艷華,李志遠,張朝煌,等. 高速角接觸球軸承靜態剛度的分析與計算[J].軸承,2005,8:1-3.

LIU Yan-hua, LI Zhi-yuan, ZHANG Chao-huang, et al.Analysis and calculation on static stiffness of high speed angular contact ball bearings[J].Bearing, 2005,8:1-3.

[6]王保民,梅雪松,胡赤兵,等.預緊高速角接觸球軸承動力學特性分析[J]. 軸承,2010,5:1-4.

WANG Bao-min, MEI Xue-song, HU Chi-bin, et al.Analysis on dynamic characteristics of preloaded high-speed angular contact ball bearings[J]. Bearing,2010,5:1-4.

[7]朱益利,金超武,許磊,等. 滾珠軸承力學模型的數值求解方法研究[J]. 中國機械工程,2013, 4: 427-431.

ZHU Yi-li, JIN Chao-wu, XU Lei, et al.Numerical solution methods of ball bearing mechanics model[J]. China Mechanical Engineering,2013,4: 427-431.

[8]陳小安,劉俊峰,陳宏,等. 計及套圈變形的電主軸角接觸球軸承動剛度分析[J]. 振動與沖擊,2013,32: 81-85.

CHEN Xiao-an, LIU Jun-feng, CHEN Hong, et al.Dynamic stiffness analysis for motorized-spindle angular contact ball bearings considering ferrule deformation[J].Journal of Vibration and Stock, 2013,32:81-85.

[9]劉良勇,李鴻亮,康正坡,等.高轉速對滾動軸承性能影響的分析與計算[J]. 軸承,2013, 2:1-4.

LIU Liang-yong, LI Hong-liang, KANG Zheng-po,et al.Analysis and calculation on effect of high rotating speed on performance for rolling bearings[J]. Bearing,2013, 2:1-4.

[10]李純潔,洪軍,張進華,等. 角接觸球軸承動剛度的實驗研究[J]. 西安交通大學學報,2013, 7: 67-72.

LI Chun-jie, HONG Jun, ZHANG Jin-hua,et al.Analysis and calculation on effect of high rotating speed on performance for rolling bearings[J]. Bearing,2013, 7: 67-72.

[11]Jones A B. Ball motion and sliding friction in ball bear [J]. Journal of Basic Engineering, 1959,81:1-12.

[12]Jones A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary laod and speed conditions [J]. Journal of Basic Engineering, 1960, 82:309-320.

[13]Gargiulo jr E P. A simple way to estimate bearing stiffness[J]. Machine Design, 1980:107-110.

[14]Kraus J, Blech J, Braun S. In situ determination of rolling bearing stiffness and damping by modal analysis [J]. Journal of Vibration, Acoustics, Stress and Reliability in Design, 1987, 109:235-240.