基于本征正交分解的氣動外形設計空間重構方法研究

?

基于本征正交分解的氣動外形設計空間重構方法研究

劉南1，白俊強1，邱亞松1，華俊2

(1．西北工業大學航空學院，陜西西安710072; 2．中國航空研究院，北京100012)

摘要:在飛行器設計過程中為了提高優化設計的尋優精度，設計變量不斷增加，從而使整個過程更加復雜且大幅延長設計周期。針對這一問題，基于本征正交分解降階方法開展氣動外形設計空間重構方面的研究。工作針對二維翼型開展，主要目標分為2個方面:①減少優化過程中的氣動外形設計參數;②提高設計空間中滿足設計約束的樣本比例。在Hicks-Henne參數化和POD重構得到設計空間內隨機選擇20 000個樣本發現，Hicks-Henne參數化空間中滿足設計約束的樣本比例不足25%，而重構之后的空間則超過70%。因此，采用POD方法對設計空間進行重構大大提高了樣本質量，同時減少了優化設計參數。以RAE2822進行厚度約束下的單目標升阻比增大優化設計為例分別研究傳統的約束處理方法和設計空間重構對優化結果的影響。傳統約束處理方法中包括罰函數法和拒絕策略，優化結果表明拒絕策略略優于罰函數法，且無須設置懲罰權重，使用方便。對比重構前后設計空間的優化結果可見，2種傳統約束處理方法在32個Hicks-Henne參數化空間中最優設計結果升阻比增加分別為27. 61%和28. 20%，采用POD方法重構后的設計空間得到的升阻比提升分別為28. 20% 和30. 63%。因此，設計空間重構前后的優化精度基本類似，而且設計空間重構之后優化設計參數大大減少，設計效率得到明顯提升。

關鍵詞:優化;參數化;效率;升阻比;本征正交分解方法;樣本質量

隨著計算機硬件水平的提高和智能優化算法的不斷完善，基于計算流體力學(computational fluid dynamics，CFD)的氣動外形智能優化已成為現代飛機設計的重要手段。為了擴大設計空間和提高設計精度，往往需要大量的優化設計變量。但是設計變量的增加不僅使整個優化設計過程更加復雜，而且會導致優化所需時間大大增加。

近年來，針對減少設計變量的參數化方法研究也逐漸引起關注。Chang等［1］基于正交函數對NACA系列的傳統翼型和超臨界翼型進行分析，結果表明采用10個正交函數能夠對超臨界翼型進行很好的描述; Robinson等［2］針對超臨界翼型采用Gram-Schmidt正交化方法得到一組正交基函數，僅使用前兩階正交基函數描述翼型，從而大大減少了設計變量; Toal等［3］使用本征正交分解方法(proper orthogonal decomposition，POD)在優化過程中對較優的設計樣本進行幾何層次上的過濾，重新構建了設計空間，明顯縮短了設計周期，但是該方法以損失設計精度為代價，可能會導致優化收斂到局部最優; Ghoman等［4］基于POD方法開展了外形參數減少的研究，結果表明本方法可以有效地減少設計變量數目并避開典型的缺陷(比如型函數選取的困難、計算效率低等原始參數化方法常見的問題)，但是沒有對設計空間的變換進行詳細討論。

與此同時，約束的處理對優化設計的效率和精度都有很大影響，目前主要的約束處理方法有——懲罰函數方法、尋找可行解方法、保留解可行性的方法以及混合方法等［5］，但是這些方法在實際應用中存在很多難題，比如傳統的罰函數方法中的懲罰系數難以確定、尋找可行解的方法很多僅適用于某一類問題等。目前在氣動外形設計中多采用罰函數一類的方法來處理約束，但是如果設計空間中不滿足約束的樣本比例很大，就會造成計算資源的浪費和設計精度的下降。

綜上所述，本文基于POD方法開展了氣動外形優化設計過程中的設計空間降維和非法樣本點過濾方面的研究。設計算例表明，相對于不作降維和過濾處理的優化設計，本文所提出的方法在保證尋優精度的前提下，有效提高了優化設計效率。

1　Hicks-Henne參數化方法

本文中對翼型的描述采用Hicks-Henne參數化方法，上下表面各采用相同數量的Hicks-Henne鼓包［6］，鼓包函數分別如下:

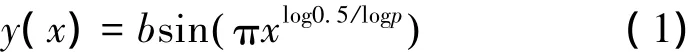
式中: b為鼓包高度，p為Hicks-Henne鼓包位置，x為翼型的x軸坐標點位置。本文中參數化翼型的各個鼓包高度變化范圍通過翼型所需的變形量來確定。很顯然，通過增加設計變量可以擴大優化設計空間，從而得到較好的優化結果，但是會延長設計周期，降低優化效率。

2　Kriging代理模型

為了提高氣動外形優化設計效率，本文采用代理模型代替耗時的N-S方程計算。常用的代理模型主要包括多項式響應面模型、人工神經元網格模型、徑向基函數模型及Kriging模型等，其中Kriging模型具有訓練樣本點處無偏估計、良好的高度非線性近似能力，非常適合作為代理模型使用，目前Kriging模型在工程優化設計領域得到了廣泛應用［7］。

Kriging模型將未知的函數用一個回歸函數B(x)和一個均值為零和方差為σ2的高斯隨機過程Z(x)組成，因此未知點的函數值^y為:

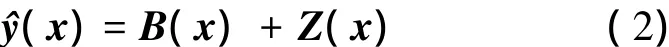
通過無偏估計和最大似然估計的方法，可以得到:

式中: B(x) = fT^B，f是已知點優化變量的函數，對于常用的零階回歸函數，f是一維數組，其值為1，^B為回歸參數，通過回歸分析可以得到。Z(x) = rT(x) R－1(y－f^B)，y是已知樣本點的函數值，R是已知樣本點處的相關矩陣，r是未知點和已知樣本點之間的相關矢量，最常采用的相關函數為Gauss函數，如下所示:

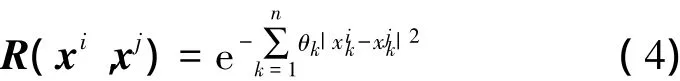
式中:θ= (θ1，θ2，…，θn)T是空間相關參數矢量，可以通過最大似然估計得到θ。

3　POD降階方法

文獻［3-4］所采用的POD是一種模型降階方法，基于“快照”的思想，從大量的樣本中提取出主要特征(基模態)［8］。

POD降階方法的主要思想是尋找一個子空間使所有“快照”{ Yi，i = 1，2，…，N} (Yi∈Rn)在該空間中的投影誤差最小。若向模態空間的正交投影關系定義為Φ: Rn→Rn，即

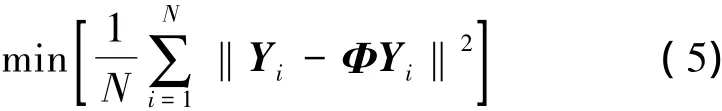
(5)式等價于尋找各階基模態{φj，j = 1，2，…，r}使

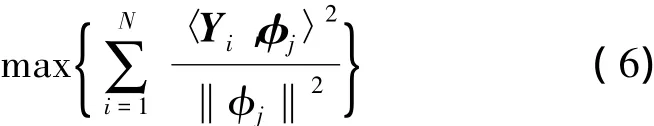
對于快照集中的所有快照均成立，其中〈·，·〉是兩向量的內積。本文選擇常用的實數域內歐式空間中的內積和范數，具體表達式如下:

計算POD基模態共有2種方法:①傳統的特征值分解降階方法，首先構造自相關矩陣并對其僅需特征分解求得各個特征值及其對應的特征向量，通過特征向量和各個“快照”即可求得各階基模態，而其所對應的特征值大小表征各階基模態所含“能量”;②奇異值分解(SVD)方法計算各階基模態。SVD方法不僅計算效率高于特征值分解POD降階方法，而且在計算高階模態時比特征值分解方法更為精確［9］，因此本文采用SVD方法，具體過程如下:

假設“快照”集為{ Yi，i = 1，2，…，N}，首先得到所有快照的均值，如下:

通過快照的脈動Y'i= Yi－珘Y構造矩陣A如下:

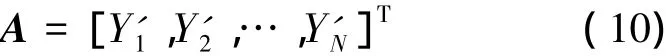
將A矩陣進行SVD分解得到:

式中，U∈RN×N，∑∈RN×n，V∈Rn×n，∑僅有對角線元素∑ii=σi，且滿足σ1≥σ2≥…≥σr≥0，其余元素全部為0。這樣就可以得到各階基模態:

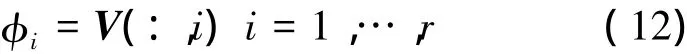
第i個“快照”可由所有基模態的線性組合得到:

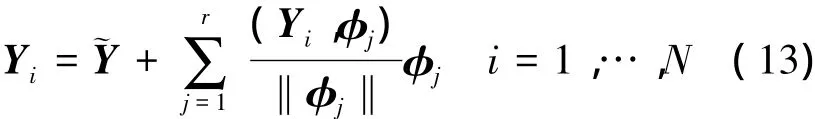
通過“能量準則”可以選擇基模態數量以近似表達各個“快照”，比如選取p個基模態使前p個基模態的“能量”之和占所有基模態“能量”之和的99. 9%以上，其中基模態的“能量”的大小以其所對應的奇異值平方表征，即

最終得到各個“快照”的近似解如下:

式中，p＜r。

4　二維翼型氣動外形優化問題

采用粒子群優化算法對RAE2822翼型進行氣動外形優化設計，設計狀態為: Ma = 0. 729，α= 2. 31°，Re = 6. 5×106。為了保證CFD計算的可靠性，計算結果和風洞試驗結果的壓力分布對比如圖1所示，計算結果對前緣吸力峰值處的小凸起、上表面壓力平臺區、壓力恢復區等吻合較好，對激波的捕捉有所欠缺，基本達到工程所需的精度要求。

設計目標和約束如下:

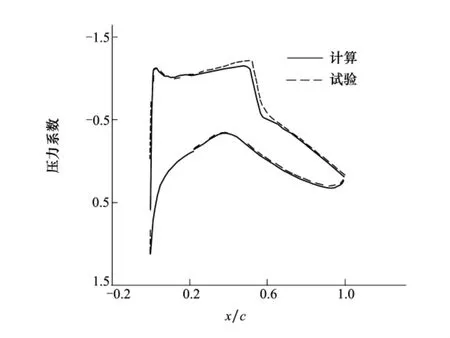
圖1　CFD計算結果與風洞試驗結果對比

式中，Cd為阻力系數，Cl為升力系數，目標函數為升阻比的倒數Cd/Cl。thickness constraints為:前梁位于0. 16c處，后梁位于0. 6c處，前梁厚度、后梁厚度和最大厚度均不小于RAE2822翼型的相應厚度。對于厚度約束，分別采用懲罰策略、拒絕策略和基于POD方法的設計空間過濾3種措施進行處理。

4. 1懲罰措施

懲罰措施是對約束進行處理的最一般的方式，是通過對不可行解的懲罰來將約束問題轉化為無約束問題。任何對于約束的違反都要在目標函數中添加懲罰項。但是在實際應用中很難確定懲罰函數的形式和懲罰權重，本文中的適應值函數如下:

式中:θ1，θ2，θ3為翼型的前梁厚度、后梁厚度和最大厚度，θo1，θo2，θo3為RAE2822翼型相應位置處的厚度。a1，a2，a3為相應的懲罰權重，為了保證懲罰強度，本文采用懲罰權重隨優化代數線性遞增的方法，a1，a2，a3的初始值均設置為0. 2，最后一代的懲罰權重為100。

4. 2拒絕策略

拒絕策略也稱為死亡懲罰，其做法是直接拒絕優化過程中所有不可行解，減小了搜索范圍。由于無需設置格外的參數，所以拒絕策略是處理約束最簡單的方法。在種群初始化中，為了保證初始種群全部滿足約束，首先采用拉丁超立方取樣方法(Latin hypercube sampling，LHS)選取大量樣本，將其中滿足約束的樣本作為初始種群;優化過程中生成新的樣本之后首先判斷其是否滿足約束，若滿足則加入種群中，否則重新生成新的樣本，直到滿足約束為止。

4. 3基于POD方法的設計空間過濾策略

為提高設計空間中滿足約束的樣本比例，對二維翼型從Hicks-Henne參數化空間向POD模態空間的轉換進行研究。具體過程如下:

1)采用LHS方法在Hicks-Henne參數空間取出大量的樣本，并判斷樣本是否滿足厚度約束，滿足則放入“快照”集中，不滿足則舍棄該樣本;

2)采用第2節中介紹的降階方法從“快照”集中提取出各階基模態，并求得所有“快照”在各階基模態上的投影系數;

3)從投影系數中提取出所有“快照”在各階基模態上投影系數的上下限，得到快照在模態空間上的投影系數的變化范圍。

這樣就把優化問題從Hicks-Henne參數化空間轉換到模態空間。具體步驟如下:首先采用Hicks-Henne參數化方法和拉丁超立方取樣方法［10］，上下表面各選16個鼓包，共有32個參數，得到20 000個翼型，其中滿足幾何約束的約占24%左右，對這些翼型進行SVD分解得到各階基模態及其對應的奇異值。圖2是得到的各階基模態的“能量”的變化情況，可見“能量”主要集中在前若干個基模態中。

圖2　POD各階模態的“能量”大小

所選取基向量的“能量”之和超過所有基向量“能量”之和的99. 9%，最終確定的基向量數目為16。

多次采用LHS方法在32維的Hicks-Henne參數化空間和16維的POD基模態空間分別獲得隨機不同的20 000個翼型樣本發現，結果如圖3所示。由圖可見，Hicks-Henne參數空間中滿足厚度約束的樣本比例約占24%，而在POD基模態空間中該比例則超過70%。由此可見，從參數化空間轉換到基模態空間之后，設計空間有所減小，許多非法的設計空間被剔除，有利于縮短優化耗時。

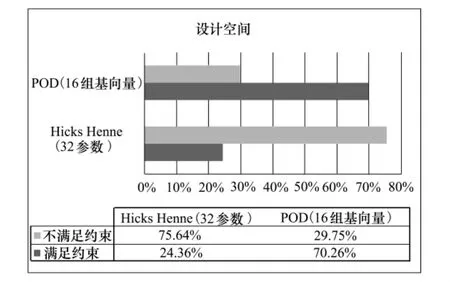
圖3　不同設計空間中取樣結果對比

5　不同設計空間優化結果對比

為了體現POD空間重構方法在優化設計中的可行性，本文采用32個Hicks-Henne鼓包構成的參數化空間和前16個POD基向量對應的設計空間分別對RAE2822翼型在厚度約束下的升阻比進行優化。

5. 1訓練Kriging代理模型

在氣動外形優化設計之前，必須首先訓練具有高可信度的Kriging代理模型，從而減少優化設計耗時，提高效率。在Hicks-Henne參數化空間和POD基模態空間中分別采用LHS方法得到500個和300個訓練樣本，以此訓練Kriging代理模型。

然后從兩個空間中隨機抽取50個測試樣本，使用已建立的代理模型對測試樣本的升力和阻力系數進行預測。在Hicks-Henne參數化空間和POD基模態空間中建立的代理模型對測試樣本升力系數預測均方根誤差分別為1. 25%、1. 46%，阻力系數預測誤差分別為2. 77%和3. 77%。其中升力系數的計算結果和預測結果對比如圖4所示。

在優化過程中適當地對代理模型進行更新以保證其精度和可靠性，本文采用的方法是每代選取3個適應值最高的樣本，采用CFD計算得到其氣動力系數，并將其加入代理模型樣本庫，對其重新進行訓練，得到新的Kriging代理模型。

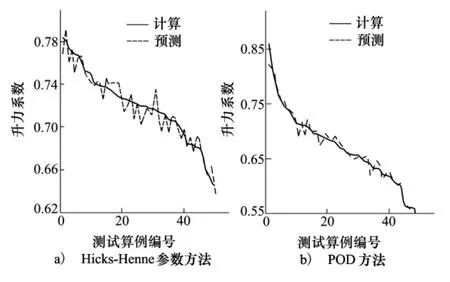
圖4　計算和預測的結果對比

5. 2優化結果

為了對比翼型優化設計在Hicks-Henne參數化空間和POD基模態空間中的不同表現，采用粒子群智能優化算法對翼型進行優化，優化代數為50代，每代種群由100個樣本構成。每種策略(Hicks-Henne參數化空間+罰函數、Hicks-Henne參數化空間+拒絕策略、POD基模態空間+罰函數、POD基模態空間+拒絕策略)優化5次，表1為每次優化得到最優構型的適應值對比。

表1　優化結果對比

由表1可見，16個POD基向量系數的優化結果略優于32個Hicks-Henne參數化方法的優化結果，而拒絕策略的結果也略好于罰函數方法。其中每種策略的最優收斂過程對比如圖5所示。

采用12核Intel(R) Xeon(R) CPU X5650 @ 2. 67GHz圖站開展優化設計，對比采用拒絕策略的Hicks-Henne方法和POD方法的優化耗時如表2所示，表中時間單位為h。優化過程中的優化耗時主要用于Kriging代理模型的更新。更新代理模型過程中需要大量調用BLAS庫函數中的向量運算程序，較為耗時。相比于Hicks-Henne方法，采用POD方法節省了約1/3的優化耗時。

圖5　收斂結果對比

表2　取樣與優化耗時對比

最終優化結果的幾何和壓力分布對比如圖6和圖7，升阻力系數見表3。4個構型的升阻比相差在2. 0以內，前緣吸力峰值壓力系數差量在0. 1以內，激波均有了明顯減弱。其中采用Hicks-Henne方法優化結果在翼型上表面70%至90%弦長位置有明顯的凸起，該凸起能夠降低逆壓梯度，采用罰函數策略的最為明顯，該優化翼型上表面基本無激波;采用POD方法得到的2個最優構型均有明顯的前加載特征;而4個優化結果在翼型下表面后緣處的后加載強度相差不大。

表3　最優結果氣動力系數對比

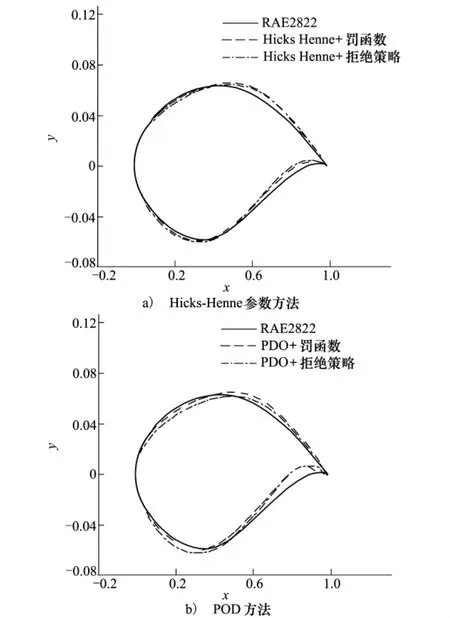
圖6　優化前后幾何外形對比

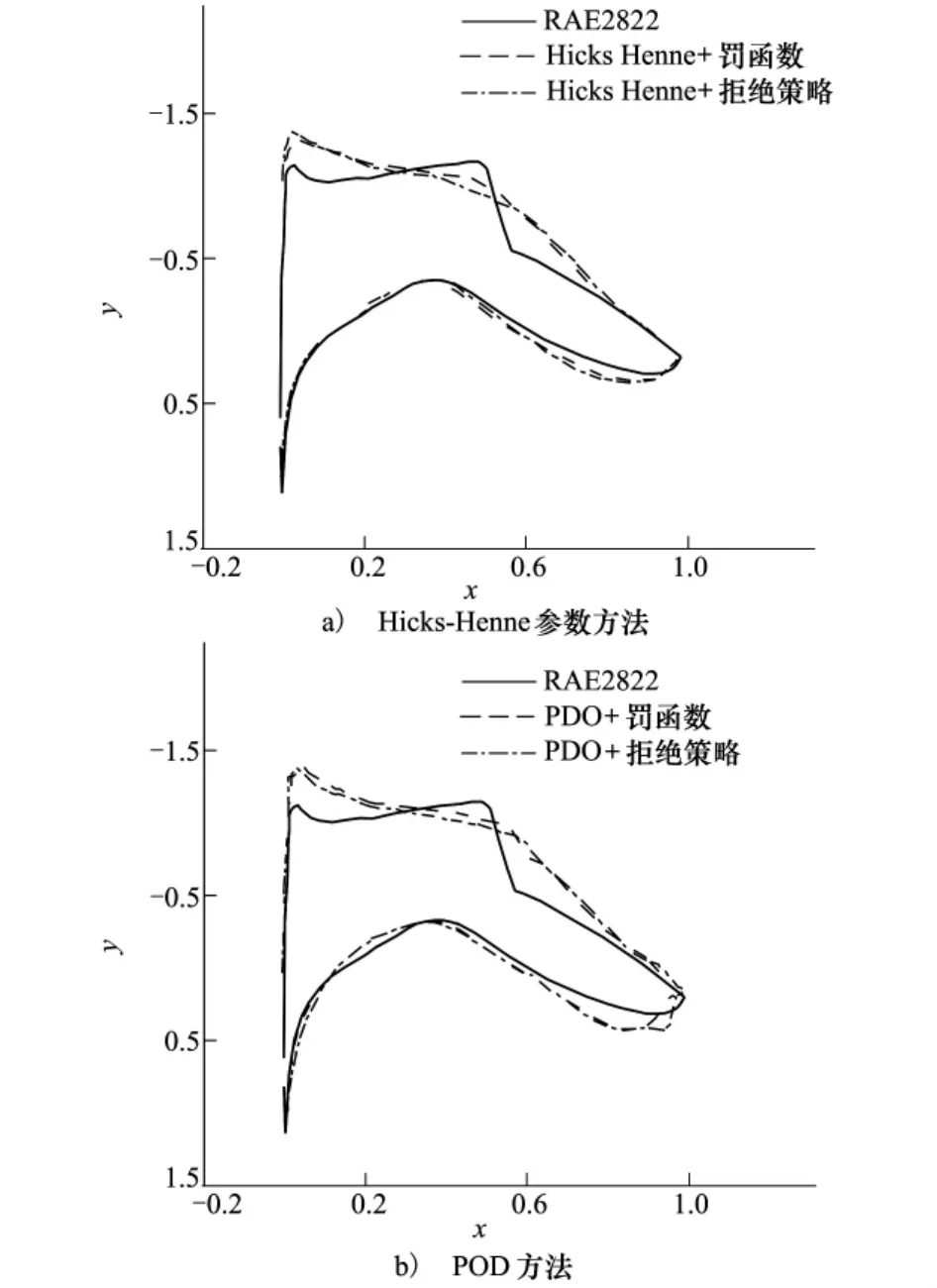
圖7　優化前后壓力分布對比

6　結論

1)對于厚度約束情況，Hicks-Henne參數化方法得到的設計空間中滿足約束的樣本約占24. 36%，而基于POD方法重構的設計空間中滿足約束的樣本約占70. 26%，大大提高了合法樣本的比例;

2)在基本不降低設計精度的前提下，基于本征正交分解方法的氣動外形優化設計空間重構能夠有效地減少了氣動外形優化設計參數，縮短設計周期，提高尋優效率;

3)目前最常用的2種懲罰策略——罰函數法和拒絕策略，罰函數方法要反復試驗方能得到較好的懲罰因子，從而提高設計精度，但是拒絕策略較為簡單。在厚度約束下RAE2822翼型單目標增加升阻比優化中拒絕策略得到的優化結果略優于罰函數法。

參考文獻:

［1］Chang I C，Torres F J，Tung C．Geometric Analysis of Wing Sections［R］．NASA Technical Memorandum 110346，1995

［2］Robinson G M，Keane A J．Concise Orthogonal Representation of Supercritical Airfoils［J］．Journal of Aircraft，2001，38(3) : 580-583

［3］Toal D J J，Bressloff N W，Keane A J，et al．Geometric Filtration Using Proper Orthogonal Decomposition for Aerodynamic Design Optimization［J］．AIAA Journal，2010，48(5) : 918-928

［4］Ghoman S S，Wang Z，Chen P C，et al．A POD-Based Reduced Order Design Scheme for Shape Optimization of Air Vehicles ［R］．AIAA-2012-1808

［5］Coello C A C．Theoretical and Numerical Constraint-Handling Techniques Used with Evolutionary Algorithms: A Survey of the State of the Art［J］．Computer Methods in Applied Mechanics and Engineering，2002，191(11/12) : 1245-1287

［6］Hicks R，Henne P．Wing Design by Numerical Optimization［J］．Journal of Aircraft，1978，15(7) : 407-413

［7］Shao T F，Krishnamurty S，Wilmes G C．Preference-Based Surrogated Modeling in Engineering Design［J］．AIAA Journal，2007，45(11) : 2688-2701

［8］Paksoy A，Apacoglu B，Aradag S．Reduced Order Modeling of Turbulent Two Dimensional Cylinder Wake with Filtered POD and Artificial Neural Networks［R］．AIAA-2011-58

［9］Bryan R，Mohan P S，Hopkins A，et al．Statistical Modelling of the Whole Human Femur Incorporating Geometric and Material Properties［J］．Medical Engineering＆Physics，2010，32: 57-65

［10］Husslage B G M，Rennen G，van Dam E R，et al．Space-Filling Latin Hypercube Designs for Computer Experiments［J］．Optim Eng，2011，12: 611-630

Investigating Aerodynamic Shape Design Space Reconstruction Using Proper Orthogonal Decomposition (POD)

Liu Nan1，Bai Junqiang1，Qiu Yasong1，Hua Jun2

(1．College of Aeronautics，Northwestern Polytechnical University，Xi'an 710072，China 2．Chinese Aeronautical Establishment，Beijing 100012，China)

Abstract:In order to increase optimization precision in the design process of aircraft，the design parameters have augmented; this makes the design process more complicated and extends the design cycle．Aiming at this issue，reconstruction method of aerodynamic design space using Proper Orthogonal Decomposition is investigated．Main objective is divided into two aspects: one is reduction of the number of aerodynamic design parameters in design process，the other is increase of the ratio of samples which satisfy design constraints．In the Hicks-Henne parameterization space and reconstructed space by POD，20000 samples are chosen by LHS method．It is illustrated that the ratio of Hicks-Henne parameterization space satisfying thickness constraints is less than 25%，while the ratio of reconstructed space by POD is about 70%．Therefore，after space reconstruction by POD，sample quality is enhanced significantly．Moreover，the number of optimization parameters is decreased．The influence of traditional constraint handling methods and reconstructed design space is investigated with the optimization of Cl/Cd of RAE2822 airfoil．Traditional constraint handling methods include penalty function method and death penalty．It is shown that death penalty method is slightly better than penalty function method from optimization results．Additionally，there are no penalty factors in death penalty process，which is convenience to use．Comparing the optimization results before and after reconstructed design space，the improvements of Cl/Cd are 27. 61% and 28. 20% respectively for two traditional penalty handing methods in Hicks-Henne parameterization space，while the improvements are 28. 51% and 30. 63% respectively in reconstructed design space by POD．Therefore，the optimization precision is almost the same before and after space reconstruction，and the number of design parameters is decreased by half; this makes design efficiency improve significantly．

Key words:aerodynamic configurations; aircraft; angle of attack; computational fluid dynamics; design; drag coefficient; efficiency; experiments; lift drag ratio; Mach number; maximum likelihood estimation; optimization; parameterization; Reynolds number; singular value decomposition; wind tunnels; Proper Orthogonal Decomposition; sample quality

作者簡介:劉南(1989—)，西北工業大學博士研究生，主要從事降階模型、氣動優化設計及氣動彈性力學研究。

收稿日期:2014-09-18

文章編號:1000-2758(2015) 02-0171-07

文獻標志碼:A

中圖分類號:V211．3