基于漸消濾波的神經網絡優化算法及其應用

?

基于漸消濾波的神經網絡優化算法及其應用

高社生，楊一，高兵兵

(西北工業大學自動化學院，陜西西安710072)

摘要:針對BP神經網絡在訓練過程中易陷入局部極小值的問題，提出一種新的基于漸消濾波的神經網絡學習算法。該算法采用漸消卡爾曼濾波對神經網絡的權值進行更新，有效避免了梯度下降算法產生的局部極小問題;與卡爾曼濾波相比，在漸消濾波中充分考慮了最新量測值的影響，能更合理地利用新的有效信息，從而提高了學習算法的收斂速度。學習后的網絡不僅具有普通神經網絡的自主學習能力，而且具有漸消濾波的最優估計性能。將提出的神經網絡算法應用于SINS/BDS組合導航系統進行仿真驗證。結果表明，提出的算法在逼近精度方面優于BP算法和卡爾曼濾波算法，可以有效提高神經網絡的泛化能力。

關鍵詞:神經網絡;漸消濾波;學習算法;組合導航

人工神經網絡因其具有拓撲結構簡單和全局逼近能力較強的特點，在時間序列預測、非線性系統建模與控制等方面得到了廣泛的應用［1-2］。在各類神經網絡模型中應用最廣泛的是前饋神經網絡，前饋網絡中最常用的是基于梯度下降法的BP (back propagation)神經網絡。然而，BP神經網絡存在以下缺點:①學習算法的收斂速度較慢，BP算法是以梯度下降法為基礎，因此只具有線性收斂速度;②學習因子η沒有可遵循的選擇規則，完全根據經驗選取;③易陷入局部極小值，從數學角度看，BP算法是一種非線性的優化問題，這就不可避免地存在局部極小問題［3-4］。

為了克服上述缺陷，文獻［5］提出基于擴展卡爾曼濾波(extended kalman filtering，EKF)的神經網絡權值更新算法。研究結果表明在逼近精度相同的情況下，該神經網絡的計算量遠小于梯度下降算法，有效克服了BP算法收斂速度慢，易陷入局部極小等問題。然而，EKF在計算過程中忽略二階以上誤差項，在系統模型非線性較強時，濾波精度嚴重降低，從而影響權值更新的精度。為了進一步提高EKF訓練神經網絡的精度，文獻［6］利用unscented卡爾曼濾波(UKF)在線調整神經網絡的權值，并證明了該方案的可行性和有效性。然而，UKF算法中UT變換迭代會增大計算量，從而影響該神經網絡算法的實時性。文獻［7］將基于輸入狀態穩定性(ISS)的學習算法應用于遞歸神經網絡，為系統辨識提供了魯棒控制技術。仿真結果表明，該算法可以有效提高非線性系統的辨識精度，并且避免了局部極小值等問題。然而，該算法僅適用于離散系統且計算量較大。漸消濾波是一種參數可自適應調節的濾波算法，能有效利用系統的最新量測信息。在進行濾波時，采用漸消因子限制Kalman濾波器的記憶長度，以便充分利用現時的觀測數據，減小陳舊觀測值的影響，從而使系統具有更好的自適應性和魯棒性［8］。

本文在研究漸消濾波和神經網絡的基礎上，提出一種新的基于漸消濾波的神經網絡學習算法(fading Kalman filtering neural network，FKFNN)。該算法利用漸消濾波對神經網絡的權值進行更新，有效地避免了局部極值問題;并且采用漸消因子使歷史狀態信息的使用效率降低，抑制濾波發散，從而提高網絡訓練的收斂速度。將該算法應用于SINS/BDS組合導航系統進行誤差估計，仿真結果驗證了該算法的有效性和實時性。

1　漸消濾波算法

1．1漸消濾波原理

設系統的狀態模型和觀測模型分別為

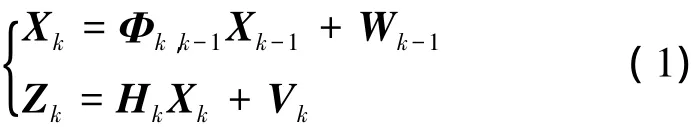
式中，Xk為系統狀態變量;Φk，k－1為tk－1時刻至tk時刻的一步轉移矩陣; Zk為量測變量; Hk為量測陣; Wk和Vk都是零均值白噪聲向量;其方差陣分別為Qk和Rk。

漸消卡爾曼濾波方程為［9］

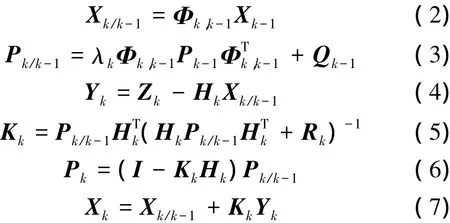
式中，λk為漸消因子，也稱遺忘因子，且λk≥1; Kk為濾波增益陣; Yk為預測殘差; Pk/k－1和Pk－1分別為預測誤差協方差矩陣和濾波協方差矩陣。(2)～(7)式所列濾波方程與標準卡爾曼方程相比，區別在于將驗前狀態協方差矩陣膨脹λk倍，使歷史狀態信息的使用效率降低，從而達到了重用現時測量信息的目的。因此，漸消濾波的關鍵是漸消因子λk的確定。

1．2漸消因子的求解

漸消濾波算法包括2類漸消因子，第1類是用最速下降法確定漸消因子，但是計算時需要經過多次迭代，且公式表示復雜，過程較繁瑣。第2類漸消因子采用一步算法，如下式所示［8］

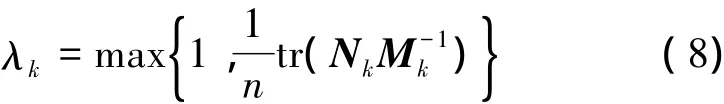
第2類漸消因子的簡化算法為

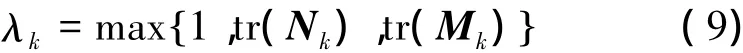
式中，tr(·)表示矩陣求跡符號，Mk和Nk的表達式為

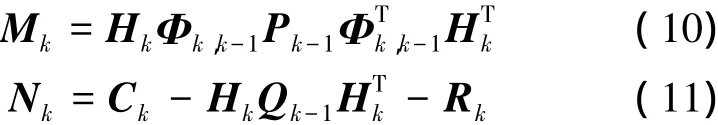
式中

式中，預測殘差Yk由(4)式給出。一般用開窗估計法確定Ck［9］，類似于Sage濾波［10］

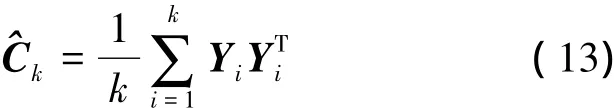
當預測殘差Yk增大，將引起Ck增大，最佳漸消因子λk也相應增大，使濾波器達到最佳。

2　一種新的漸消濾波神經網絡

2．1BP神經網絡

BP神經網絡由輸入層、若干隱層和輸出層組成，其中輸入層由線性神經元組成，隱含層和輸出層神經元是Sigmoid函數。3層BP神經網絡結構如圖1所示［11］。

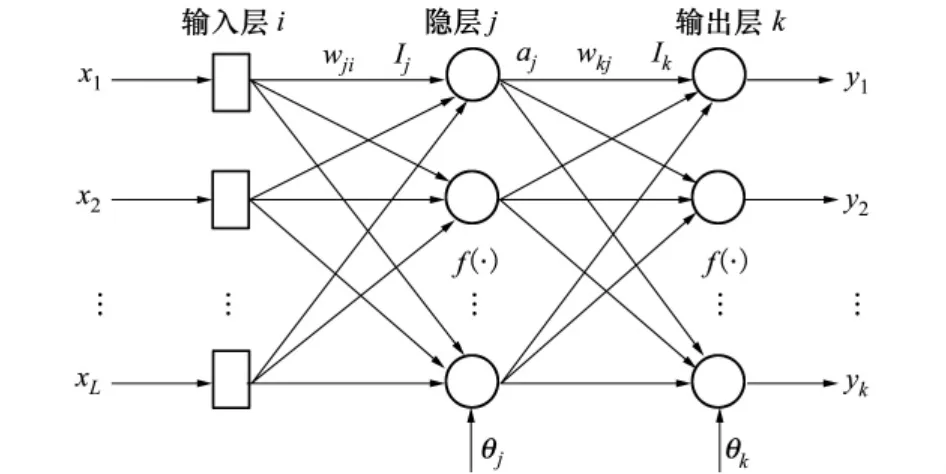
圖1　BP神經網絡結構圖

由圖1可以看出，3層前向網絡的傳遞關系為

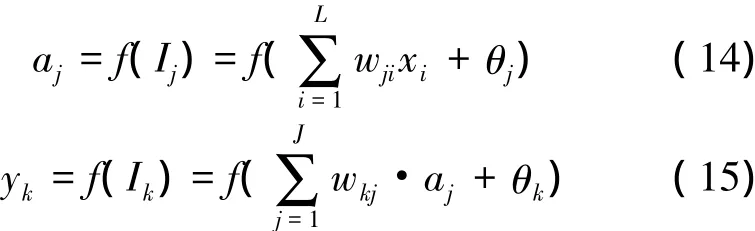
式中，wji為輸入層的第i個神經元到隱含層第j個神經元的連接權;θj為隱含層第j個神經元的閾值; wkj為隱含層的第j個神經元到輸出層的第k個神經元的連接權;θk是輸出層第k個神經元的閾值; f(·)為S型激活函數，滿足

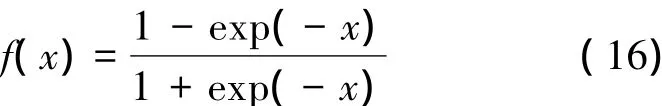
傳統的BP神經網絡通常采用誤差反向傳播法調整連接權。設神經網絡的目標函數為

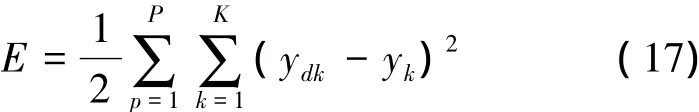
式中，ydk表示神經元k的期望輸出，p表示訓練樣本數。

隱含層與輸出層的連接權值更新公式為輸入層與隱含層的連接權值更新公式為

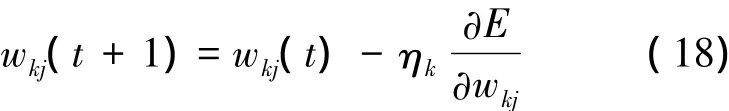
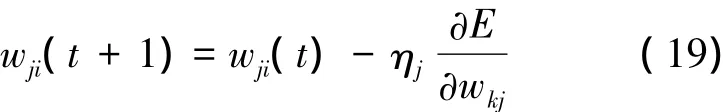
式中，ηj，ηk均為學習速率系數，即學習因子。

2．2漸消濾波學習算法

由于輸出誤差和連接權值之間存在非線性函數的關系，所以梯度下降算法在處理權值更新時收斂速度較慢。考慮將每個神經元的非線性問題轉化為線性問題求解。神經元由加權和輸出與S型激活函數兩部分組成，前一部分是權重的線性函數，后一部分為權重的非線性函數。以輸出層節點k為例，當所有節點的函數輸出yk以及加權和輸入Ik確定時，可以用權矢量wk與隱含層輸出以及節點的加權和輸入Ik組成一個線性系統模型。

以輸出層的一個神經元k為例，假設其連接權wk作為狀態變量，該神經元的加權和輸入作為量測值。對于一組學習樣本，在訓練迭代達到(t－1)次時，狀態和量測的一步預測為

式中，vk是網絡的量測噪聲。wk是(j + 1)維列向量; S是(j + 1)維行向量，分別由下式表示

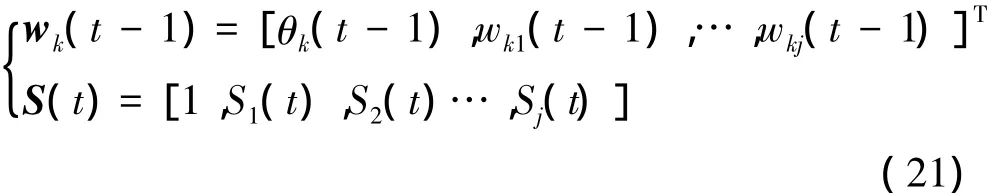
式中，wkj(t－1)表示第(t－1)次迭代時輸出層神經元k與隱層各節點的連接權值; S(t)表示隱層各神經元的函數輸出;θk(t－1)為第(t－1)次迭代時輸出層神經元k的閾值。

假設在第t次迭代時，輸出層神經元k的目標輸出及輸出層的加權和輸入分別為ydk(t)和Ik(t/t－1)，則量測值為

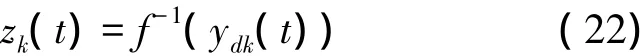
此時，(4)式中的預測殘差為

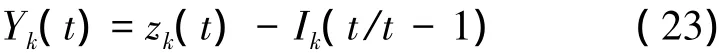
對于輸出層的第k個節點，可得權向量在第t次迭代時的漸消濾波遞推公式為

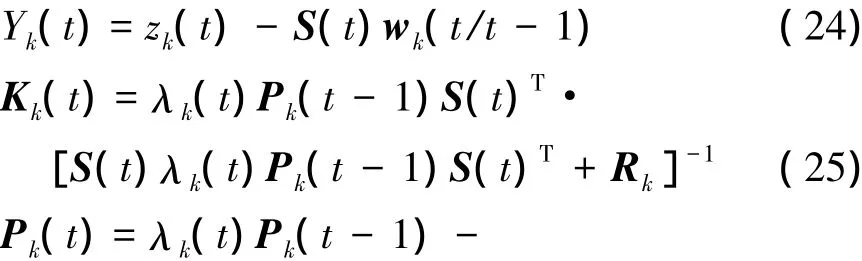
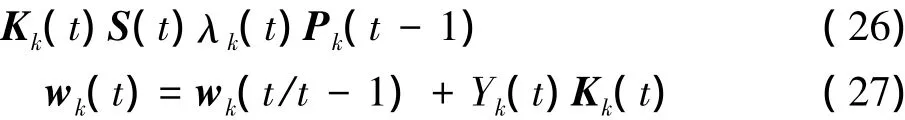
式中，Pk為權值估計的均方誤差，初始值Pk(0)在計算中給出; Kk為增益矩陣;λk為漸消因子，其值由(9)～(13)式求取。

根據上述遞推公式，FKFNN學習算法的步驟可歸納如下:

1)初始化

設置各神經元的閾值偏置為任意非零常值;網絡所有連接權值為小的隨機數;初始方差陣為對角矩陣;

2)提供訓練樣本

選擇網絡輸入和輸出樣本對，輸入樣本及目標輸出樣本分別為x和ydk;

3)訓練神經網絡

根據輸入輸出樣本對網絡進行訓練，計算網絡輸出層的加權和輸入為

Ik(t/t－1) = S(t) wk(t/t－1)

4)調用漸消濾波遞推方程計算漸消濾波的增益

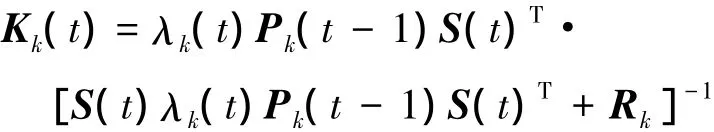
計算更新的誤差協方差陣

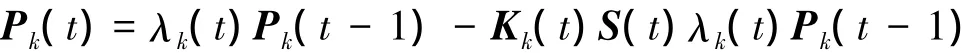
式中，λk(t)為第t次迭代時的漸消因子，由(9)～(13)式求取。

5)求解網絡輸出層的目標加權和輸入，即漸消濾波量測量為

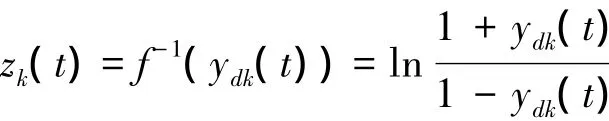
6)權值的更新

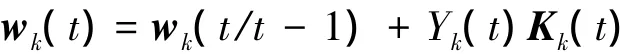
7)重復步驟(2)～(6)，直至均方誤差或訓練次數滿足要求，訓練結束。

在前向神經網絡學習中，非線性特性的學習主要由隱層和輸出層完成，因此本文提出的基于漸消濾波的權值更新算法僅用于隱含層和輸出層之間的權值和閾值。對于輸入層和隱含層之間的連接權值及閥值仍采用BP算法進行更新。這樣可以在提高網絡學習精度的同時，減小算法的計算復雜度，有利于算法的實時性。

3　仿真實驗及分析

將提出的FKFNN學習算法應用于SINS/BDS (strapdown inertial navigation system/ Beidou system)組合導航系統中，并與BP算法和基于KF的神經網絡學習算法(KFNN)進行仿真比較。SINS/BDS組合導航系統兼備了SINS和BDS的優點，能夠克服各導航子系統的缺陷，提高整個導航系統的性能。以SINS輸出參數的誤差量作為系統狀態變量，系統的量測量由SINS輸出的位置和速度信息與BDS輸出的對應信息相減獲得，并選取東北天(E，N，U)地理坐標系為導航坐標系。組合導航狀態方程和量測方程見文獻［11］。

作為仿真算例，采用SINS/BDS組合導航系統漸消卡爾曼濾波方程為神經網絡提供仿真實驗所需的訓練樣本。隨機選取5 000對歷元數據作為訓練樣本，2 000個歷元數據作為測試樣本。根據上述分析，設計3層前向神經網絡模型，網絡的輸入為量測量，輸出為漸消卡爾曼濾法的狀態量［11］。由組合導航系統的動力學模型確定輸入和輸出的節點數分別為6和2。隱含層神經元個數根據系統復雜程度、網絡訓練目標的精度以及訓練速度等因素綜合確定。通過多次實驗，本文最終確定神經網絡結構為6-12-9。系統采樣周期T= 1 s。當網絡輸出與目標值間的誤差滿足要求時，訓練結束。網絡的權值也隨之確定，此時輸入一組新的樣本，可用該神經網絡對系統進行精確估計。

設飛行器的初始位置為東經109°，北緯34°，飛行過程包括滑跑加速、拉起、改平、轉彎等過程，初始高度為1 000 m，平飛速度為400 m/s。飛行仿真軌跡如圖2所示，仿真時間取2 000 s。假設陀螺的隨機漂移為0．01(°) /h，隨機游走為0．001(°)/。加速度常值誤差為10－4g，隨機游走為10－5g/。SINS初始速度誤差為0．5 m/s，初始位置誤差為15 m; BDS位置誤差均方根為10 m，速度誤差均方根為0．3 m/s;東向和北向定位誤差的仿真結果如圖3～圖5所示。

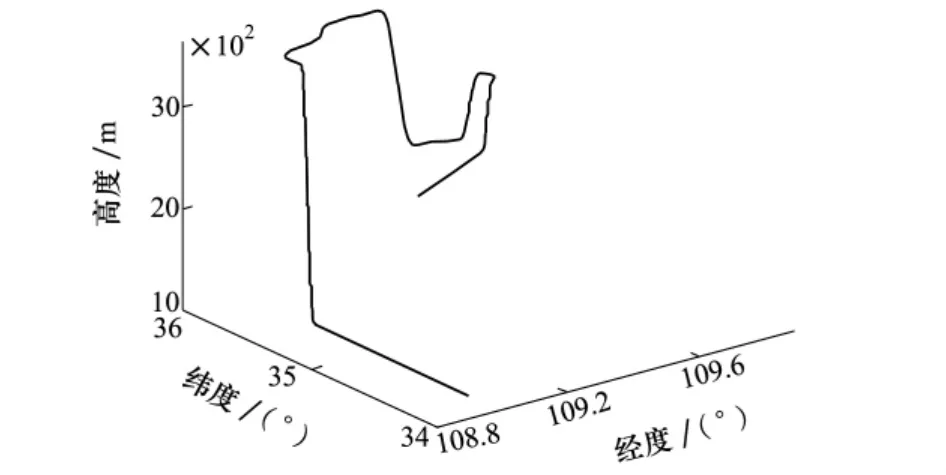
圖2　飛行器飛行軌跡

從仿真結果可以看出，BP神經網絡得到的位置誤差曲線波動較大，約在［－9 m，+9 m］之間，其峰值超過了±10 m。基于卡爾曼濾波的神經網絡得到的位置誤差約在［－7 m，+7 m］之間，相比BP神經網絡，其精度有一定提高。這是因為KF訓練神經網絡避免了陷入局部極小值的問題，提高了神經網絡的泛化能力。與KF訓練的神經網絡相比，本文提出的漸消濾波神經網絡算法得到的位置誤差更小，大約控制在［－6 m，+6 m］之內。這是因為漸消濾波可以根據每次計算信息確定漸消因子，將驗前狀態協方差矩陣膨脹λk倍，調整歷史狀態信息和現時測量信息對濾波估值的貢獻，從而提高了計算精度。

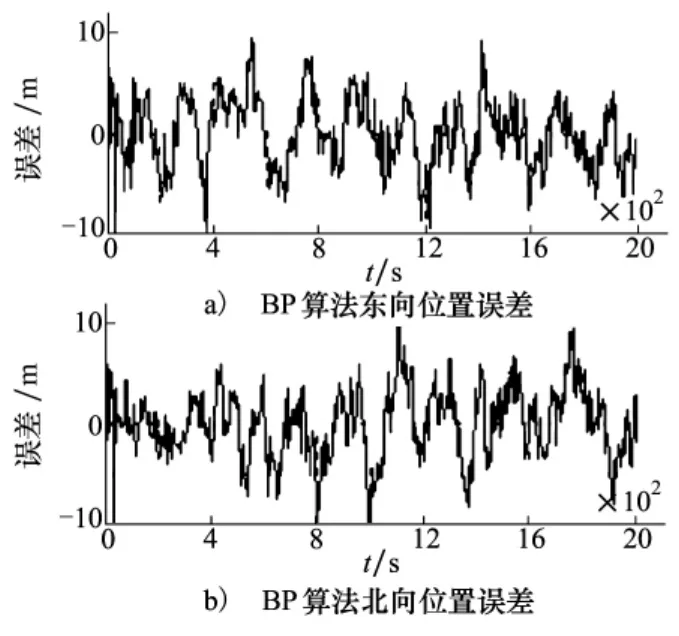
圖3　BP算法位置誤差

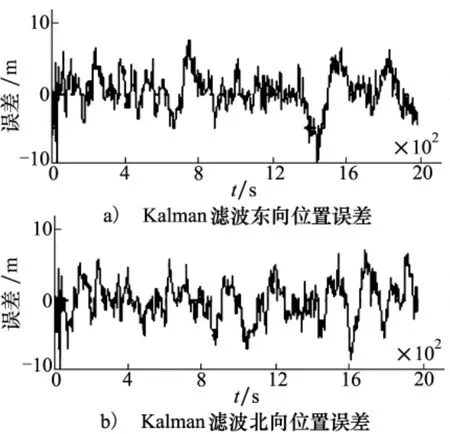
圖4　KF算法位置誤差

圖5　FKF算法位置誤差

表1　組合導航系統誤差統計

4　結論

針對BP神經網絡在訓練中易陷入局部極小點的問題，提出一種基于漸消濾波的神經網絡學習算法。該算法利用漸消濾波對神經網絡權值進行更新，有效避免了局部極小值問題;并且采用漸消因子將驗前狀態協方差矩陣膨脹λ倍，使歷史狀態信息的使用效率降低，減小陳舊觀測值的影響，從而提高計算的精度。最后，將該算法應用于SINS/BDS組合導航系統進行仿真驗證。結果表明，提出的算法在一定程度上克服了BP神經網絡的缺點;且改善了神經網絡的泛化能力，從而提高了組合導航系統的解算精度。

參考文獻:

［1］Aboelmagd N，Ahmed E，Mohamed B．GPS/INS Integration Utilizing Dynamic Neural Networks for Vehicular Navigation［J］．Information Fusion，2011，12(1) : 48-57

［2］Alsmadi M K，Noah S A．Back Propagation Algorithm: The Best Algorithm among the Multi-Layer Perceptron Algorithm［J］．International Journal of Computer Science and Network Security，2009，9(4) : 378-383

［3］Hamid M，Nitin K T．Cascading Artificial Neural Networks Optimized by Genetic Algorithm and Integrated with Global Navigation Satellite System to Offer Accurate Ubiquitous in Urban Environment［J］．Computers，Environment and Urban Systems，2013，37(1) : 35-44

［4］Azami H，Sanei S，Mohammadi K．Improved the Neural Network Training for Face Recognition Using Adaptive Learning Rate，Resilient Back Propagation and Conjugate Gradient Algorithm［J］．Journal of Computer Applications，2011，34(2) : 22-26

［5］Daniel J S．Training Radial Basis Neural Networks with the Extended Kalman Filter［J］．Neurocomputing，2002，48(1/2/3/4) : 455-475

［6］馬野，王孝通，戴耀．基于UKF的神經網絡自適應全局信息融合方法［J］．電子學報，2005，33(10) : 1914-1916

Ma Ye，Wang Xiaotong，Dai Yao．Study on Nonlinear Optimal Estimation for Neural Networks Data Fusion［J］．Acta Electronica Sinica，2005，33(10) : 1914-1916 (in Chinese)

［7］Wen Y．Nonlinear System Identification Using Discrete-Time Recurrent Neural Networks with Stable Learning Algorithm［J］．Information Science，2004，158: 131-147

［8］高社生，薛麗，魏文輝．漸消自適應Unscented粒子濾波及其在組合導航中的應用［J］．西北工業大學學報，2012，30(1) : 27-31

Gao Shesheng，Xue Li，Wei Wenhui．Fading Adaptive UPF(Unscented Particle Filtering) Algorithm and Its Application to Integrated Navigation［J］．Journal of Northwestern Polytechnical University，2012，30(1) : 27-31 (in Chinese)

［9］夏啟軍，孫優賢，周春暉．漸消卡爾曼濾波器的最佳自適應算法及其應用［J］．自動化學報，1990，16(3) : 210-216

Xia Qijun，Sun Youxian，Zhou Chunhui．An Optimal Adaptive Algorithm for Fading Kalman Filter and Its Application［J］．Acta Automatic Sinica，1990，16(3) : 210-216 (in Chinese)

［10］Yang Y，Xu T．An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Component［J］．The Journal of Navigation，2003，56(2) : 231-240

［11］楊一，高社生，吳佳鵬，等．模型預測前向神經網絡算法及其在組合導航中的應用［J］．中國慣性技術學報，2014，22(2) : 221-226

Yang Yi，Gao Shesheng，Wu Jiapeng，et al．Feed-Forward Neural Network Algorithm Based on Model Predictive Filtering and Its Application in Integrated Navigation［J］．Journal of Chinese Inertial Technology，2014，22(2) : 221-226 (in Chinese)

Neural Network Learning Algorithm Based on Fading Kalman Filtering and Its Application

Gao Shesheng，Yang Yi，Gao Bingbing

(Department of Automatic Control，Northwester Polytechnical University，Xi'an 710072，China)

Abstract:Aiming at the local minimum problem in the training process of BP neural network，this paper proposes a novel neural network learning algorithm based on the fading Kalman filtering．This algorithm avoids the problem of local minimum value because it provides the fading Kalman filtering for weights optimizing in neural network training．Compared with Kalman filtering，the fading Kalman filtering gives full consideration to the effects of the newest measurements and uses the effective information more reasonably．Consequently，the convergence speed of the algorithm is improved．The network after training not only has the autonomous learning ability of general neural network，but also has optimal estimation performance of the fading Kalman filtering．The proposed algorithm is applied to SINS/BDS integrated navigation system．Simulation results and their analysis demonstrate preliminarily that the approximation accuracy of the proposed learning algorithm is better than those of BP algorithm and Kalman filtering algorithm．The proposed algorithm，we believe，can improve the generalization capability of neural network effectively．

Key words:algorithms; back propagation algorithms，convergence of numerical methods，covariance matrix，efficiency，error analysis，errors，navigation，neural networks，fading factor，fading Kalman filtering，learning algorithm，integrated navigation，SINS/BDS(Strapdown Inertial Navigation System/ BeiDou System)

作者簡介:高社生(1956—)，西北工業大學教授、博士生導師，主要從事導航、制導與控制的研究。

收稿日期:2014-09-18基金項目:國家自然科學基金(61174193)資助

文章編號:1000-2758(2015) 02-0320-06

文獻標志碼:A

中圖分類號:TP301．6