疊加相干態與疊加壓縮態的相位精度研究

?

疊加相干態與疊加壓縮態的相位精度研究

謝端1，苗瑞霞1，趙健2

(1．西安郵電大學電子工程學院，陜西西安710121; 2．西北大學信息科學與技術學院，陜西西安710069)

摘要:利用Cramér-Rao下界法計算了疊加相干態與疊加壓縮態可以達到的最優相位精度。結果表明，平均粒子數較大時，疊加相干態的精度只能達到標準量子極限，而疊加壓縮態精度更高，達到了海森伯格極限。應用損耗模型，分析了二態在有損信道中傳輸所受到的影響。研究顯示2種量子態的精度都會有所下降。最后又加入了相干態與壓縮態，將4種量子狀態進行比較。比較結果顯示，當各態平均粒子數較大時，壓縮態與疊加壓縮態精度較高。當平均粒子數較小時，隨著損耗的增加，疊加壓縮態對外界環境的影響顯得很敏感，其精度衰減得更快些。

關鍵詞:相位精度;疊加相干態;疊加壓縮態;有損信道

由于利用量子測量方法，可以得到很高的參數精度。近些年來，人們利用該方法在原子光譜分析［1］、磁力測量［2］、光學干涉測量［3］等領域進行了研究和實驗，并取得一定成果。

理論證明，對經典量子態的參數(如相位)進行測量，其精度正比于1/，也即達到標準量子極限。而利用一些非經典的量子態，其測量精度正比于1/n，可以達到海森伯格極限。這里n指的是量子態中所包含的平均粒子數。

糾纏態和壓縮態是2種重要的非經典量子態，一些研究已證明利用這2種量子態可以將測量精度提高到海森伯格極限［4］。而非經典的量子態很多，其它類型的量子態是否也可以使測量精度達到海森伯格極限。為此，本文選取了2種典型的非經典量子態，疊加相干態和疊加壓縮態，研究它們用于測量所可能達到的最優精度。一般的，若有2種狀態| ψ+＞和|ψ－＞，其宏觀上可區分，它們疊加后形式為|ψ＞∝|ψ+＞+|ψ－＞，疊加態|ψ＞也稱為薛定諤貓態。NOON態是一種糾纏態，它同時也是一種薛定諤貓態。薛定諤貓態在量子測量甚至在整個量子力學領域，都有著重要的地位和作用。近年來，貓態吸引了很多學者目光，尤其是疊加相干態和疊加壓縮態［5-6］。Ourjoumtsev等人報道其已在實驗室成功制備了疊加相干態和疊加壓縮態［7-8］。

實際應用中，量子態在傳輸過程中不可避免地會與信道發生作用，產生損耗。雖然先期有關損耗對精度影響的研究文獻較少，但已有的少許研究顯示，一些量子態非常易受有損信道的影響，其精度會大幅下降［9-11］。舉例來說，若NOON態在傳輸中損失一個粒子，最終會變成(|N－1，0＞＜N－1，0 +0，N－1＞＜0，N－1|) /2，也即從純態變為混合態，這會造成較大的測量誤差。因此本文還將研究在量子光學通信系統中，光子損耗對測量精度的影響。我們會建立一個有損信道模型，分析常見量子態在損耗情況下可能達到的相位精度。該損耗模型，主要基于一個反射系數可調的分束器，其反射系數的大小與損耗程度的高低相應。

1　無損耗情況下疊加相干態與疊加壓縮態的相位精度分析

1. 1Cramér-Rao下界法

本文需要利用Cramér-Rao下界法確定量子態精度。量子測量學主要任務是把隱含在量子態ρx中的某一參量x提取出來。在量子態測量中，這一參量可以是相位。量子測量又可以分為2步:對某一量子系統S進行測量，得到數據結果;再分析測量結果以便提取出x的值。對量子態的測量可以采用POVM測量。POVM測量需有一個正定算符集合{ Ex}，并且算符之和滿足Ex= I。如果對n個量子態ρx進行測量，得到結果y的條件幾率為pn(y | x) = Tr()。對結果y進行數據分析可以得到估計值z。我們希望估計值z能夠非常接近真實值x。然而，實際估計值與真實值之間會有一定的誤差。假使測量是漸進無偏的，該誤差可表示為

式中，右邊的值就是Cramér-Rao下界［12］。要使(1)式成立，必須保證測量樣本v→∞［13］。另外要指出，(1)式中，I(x)就是Fisher信息量。它可以表示為

可見要得到誤差值(精度)，計算出Fisher信息量是關鍵。

1. 2疊加相干態精度估計

疊加相干態如下式所示

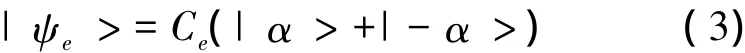
式中，Ce是歸一化常數

簡單起見，取α為實數。由于時間演化，|ψe(θ)＞可以表示為

通過對此演化態的POVM測量，就可確定相位θ值。我們要選擇一個正定算符集合{ Eχ}，并使它滿足∑χEχ= I。在此，選擇Holevo正則相位測量元［14］，它可以表示為

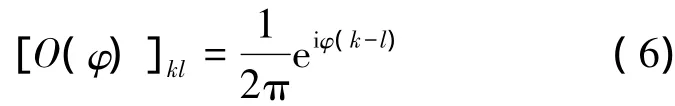
式中，［O(φ)］kl=＜k | O(φ) | l＞，可以驗證其滿足完備性∫O(φ) dφ= I。

對于疊加相干態，結果為φ的條件幾率為

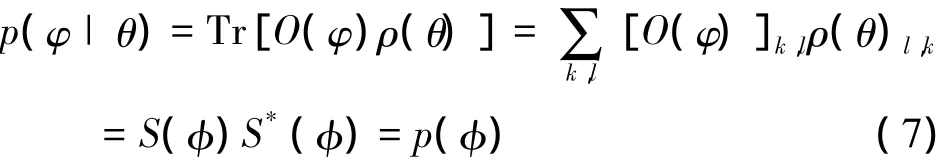
式中，φ=φ－θ。要得到條件幾率，首先要求得S(φ)的值。先考慮α較大的情況，簡單計算可以得到

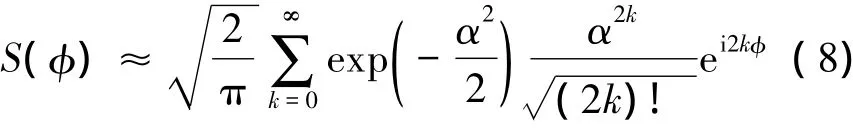
在(9)式中，我們用正態分布近似了泊松分布，再利用積分公式［15］

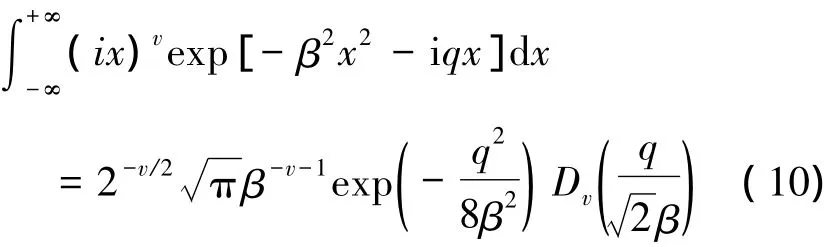
以及拋物柱面方程的漸進特性

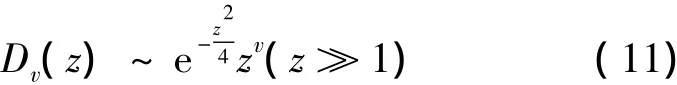
可以得到

因此

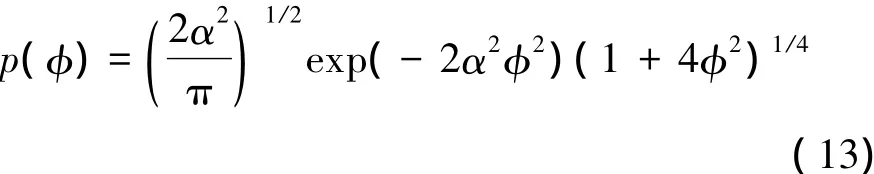
將公式(13)代入(2)式，可以得到

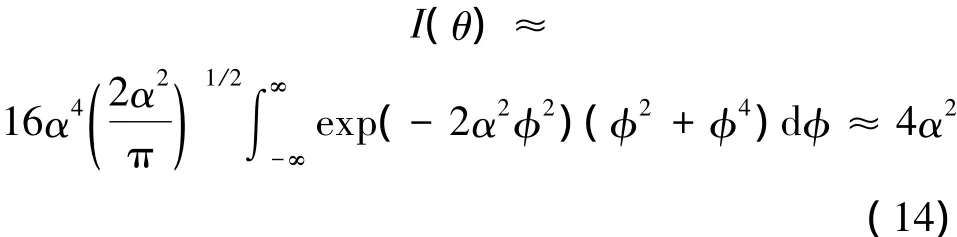
所以最優的精度為

當α較小時(α?1)，由(7)式計算p(φ)時，只精確到α的一次項，有

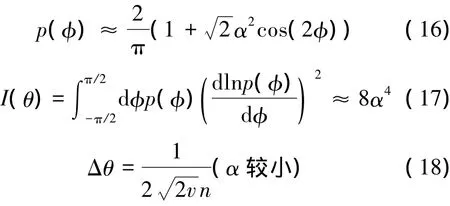
下面將精度的表達式轉化為其與平均粒子數nsc的關系。當α較大時，疊加壓縮態的平均粒子數為nsc=α2= n;而當α較小時，平均粒子數為nsc= 0. 5α2= 0. 5n。用平均粒子數來表示精度，可以得到

當平均粒子數較大時，疊加相干態的精度達到標準量子極限。

1. 3疊加壓縮態精度估計

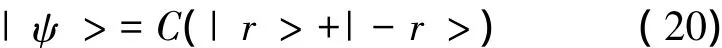
歸一化因子。由于時間演化，將會產生一個相移θ。演化后的狀態可以表示為

(21)式中。我們要將|ψ(θ)＞中所含的相位信息提取出來。對于疊加壓縮態，其Holevo正則測量元為

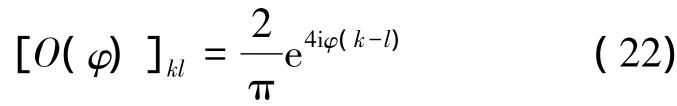
它滿足完備性∫O(φ) dφ= I。可以求得

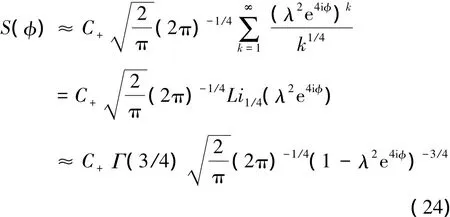
由此，可以得到

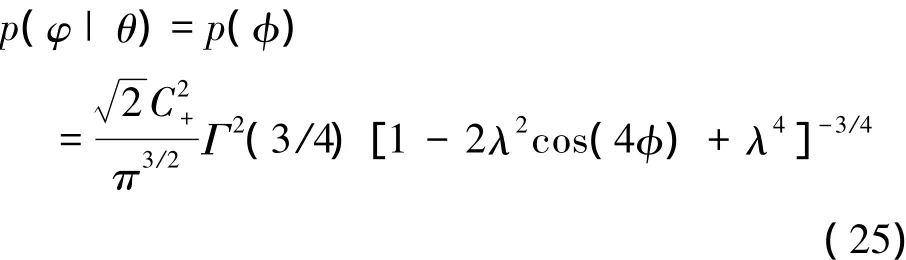
將(25)式代入(2)式，可以得到費舍爾信息量

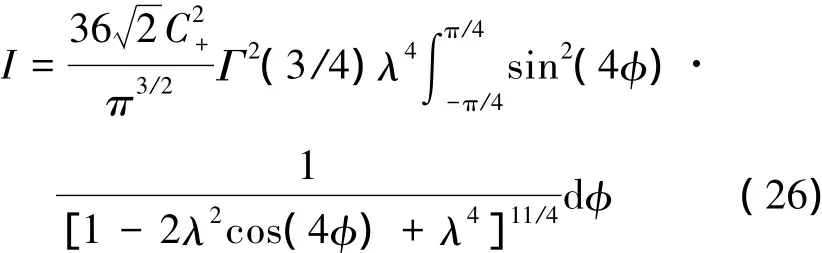
由于λ→1，在φ→0附近積分函數對積分的貢獻較大。可以將積分限從π/4拓展到∞，這樣就有

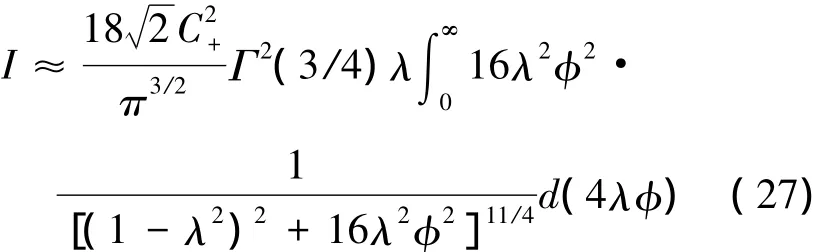
最終可以得到

所以最優的精度為

相反情況下，如果處于小壓縮極限，有n?1。在此極限下λ≈，在計算條件幾率時，只需展開到λ2項。這樣近似的幾率為

因此

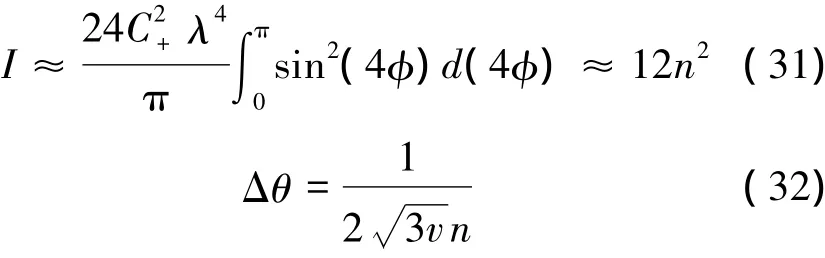
當λ→1，也即n較大時，疊加壓縮態的平均粒子數為nss= n;小壓縮極限下，nss= 0. 5n。綜上分析，疊加壓縮態的精度值為

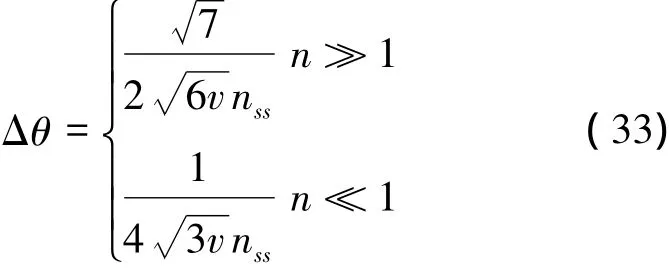
2　有損信道對量子態的精度影響分析

2. 1疊加相干態的損耗分析

量子光學已在近些年中快速發展，其傳播信道可以是光纖或是自由空間。但無論何種類型的信道，都會有光子損耗。本節我們搭建一個簡單的光子損耗模型，以此來研究疊加相干態的精度受損耗的影響。

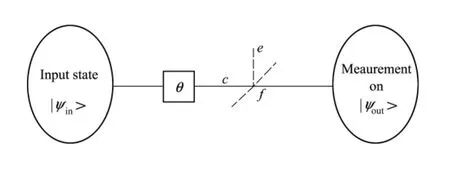
圖1　光子損耗模型

在圖1中，初態會經過一個延遲器與一個分束器到達檢測端。量子幺正操作或是其隨時間演化可以看作是一個相移θ。光子的損耗可由一個假想的分束器來描述，該分束器透射系數可調。假設其透射系數為η，則c端口湮滅算符為ac→+ae［16］。其中ai(i = c，f，e)分別為每個端口的湮滅算符。例如一個疊加相干態與環境相耦合，其可以表示為

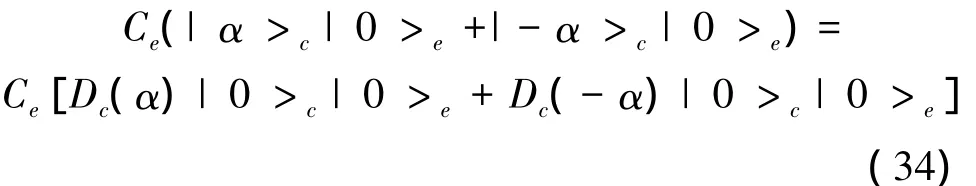
式中，Dc(α)為位移算符，其值為exp(－α*ac)。將ac→af+ae代入Dc(α)，可以得到

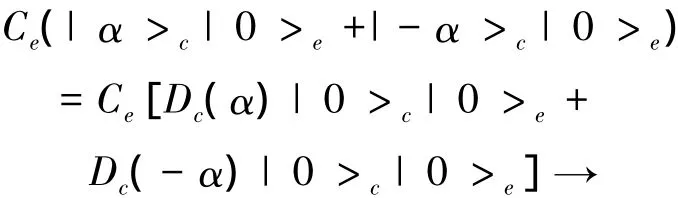
對環境e取偏跡得

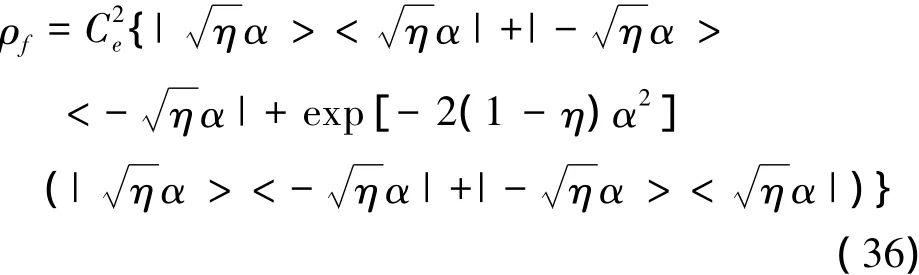
(36)式可以看作是4項相加。當α較大時，可以將后2項忽略，則有

將該狀態展開成Fock態的形式

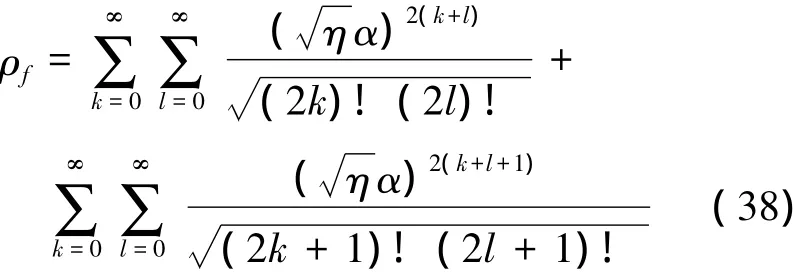
可以求得

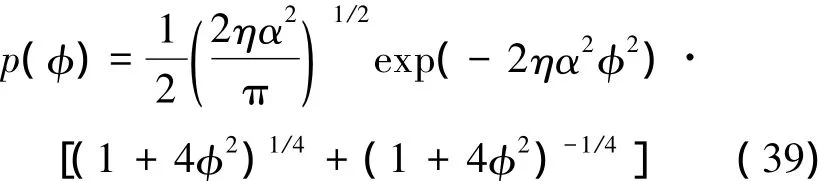
因為φ通常是一個很小的值，所以

代入到(2)式中，得

當α較小時，對(38)式只計算到α2項，有

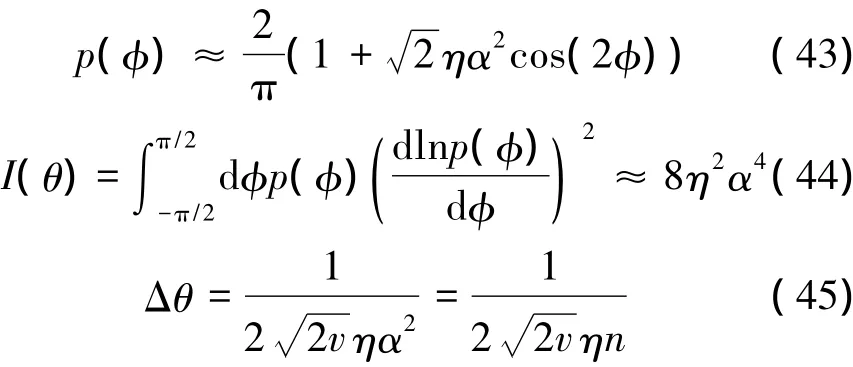
用平均粒子數來表示精度，可以得到

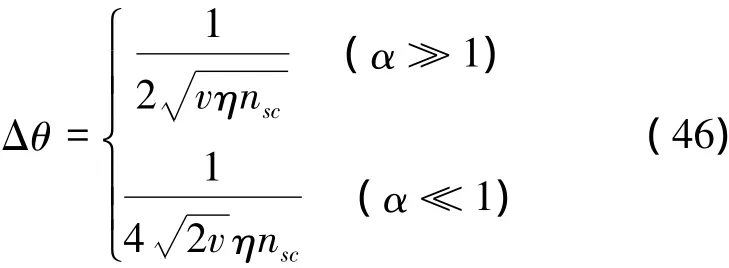
2. 2疊加壓縮態的損耗分析

與上面疊加相干態損耗分析類似。當疊加壓縮態經過分束器，對環境取偏跡，得到

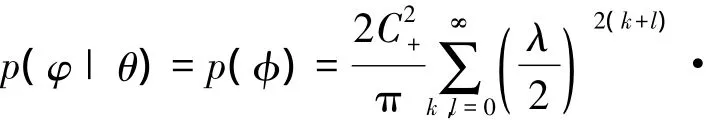
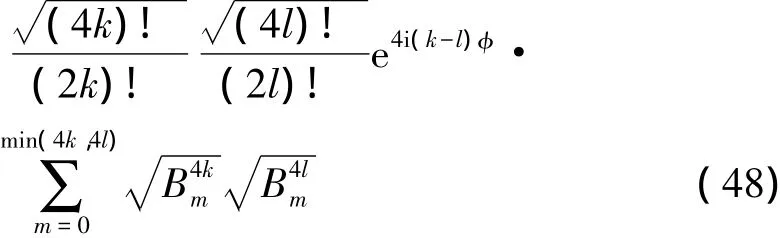
令s = k + l，u = k－l。可簡化得到

將(50)式代入(2)式，得

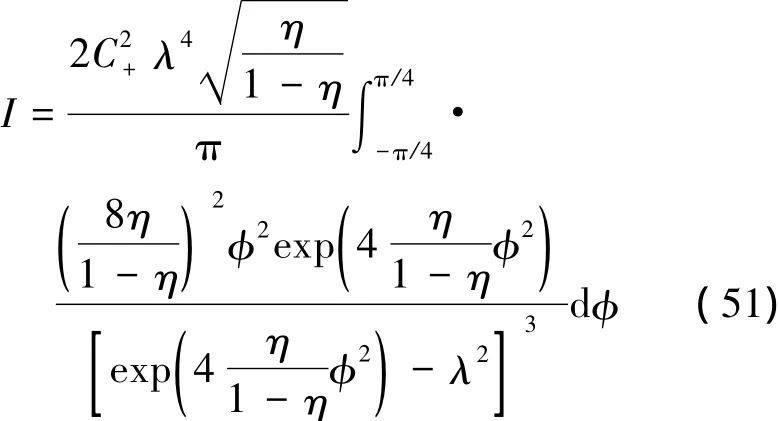
大壓縮極限下，λ→1，此時被積函數在φ較小時對積分貢獻較大。在此情況下，有近似λ2≈1－和≈。將積分限擴展到(－∞，+∞)，得到

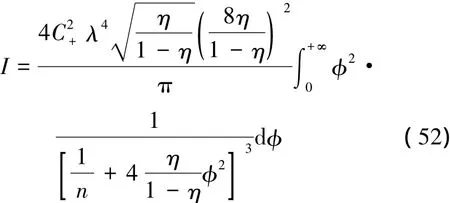
利用積分公式［17］

最終得到

所以，最優相位為

這樣，可得到

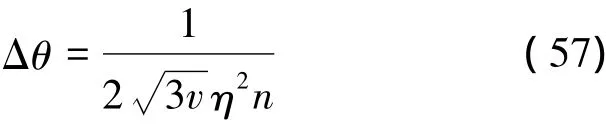
綜上分析，疊加壓縮態的精度值為

3　結果分析與比較

在這一節中，我們將對比相干態，壓縮態及它們的疊加態的精度。省略推導過程，受損耗影響，相干態與壓縮態精度分別如(59)式和(60)式所示

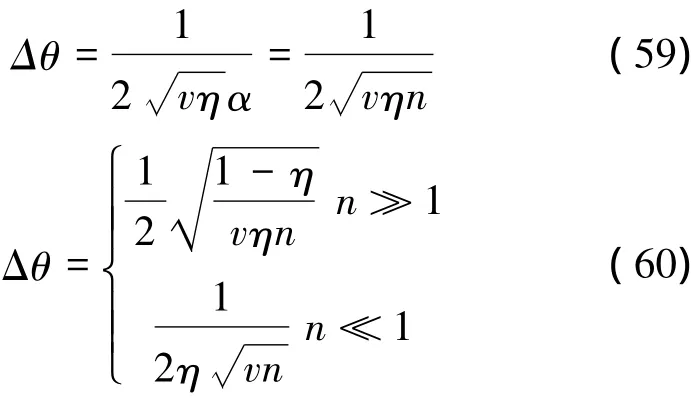
圖2顯示了當平均粒子數較大時，4種量子態的精度隨η值的變化。我們取平均粒子數為100的情況進行比較。相干態和壓縮態分別與其疊加形式的精度相同，它們隨著η值的減小(也即有損程度的增加)，精度不斷下降。由于當0＜η＜1時，＜，故而壓縮態與疊加壓縮態精度較高。圖2中還有2條水平虛線，它們分別表示在平均粒子數為100時，相干態與壓縮態通過理想信道所能達到的精度。對比發現，隨著η值的減小，2條精度變化曲線與理想信道的精度偏離越來越大。由于當η= 0. 5時= 1，此時壓縮態與疊加壓縮態精度從海森伯格極限降低到標準量子極限。當η值進一步減小時，它們的精度繼續降低，甚至會低于理想情況下相干態所達到的標準量子極限。

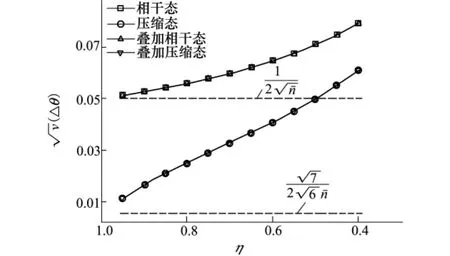
圖2　有損信道對各量子態精度影響(平均粒子數=100)

圖3又對比了在另一種極限下(也即平均粒子數較小時)，各態精度隨損耗的變化，此時各態的精度皆不相同。當(平均粒子數)和η均處于0到1區間范圍內時，有1/η2＞1/ηn珔＞1/η＞1/，故而疊加壓縮態的精度隨損耗的增加降低的最快，其次是疊加相干態，再次是壓縮態，最后是相干態。在平均粒子數較小時，疊加壓縮態和疊加相干態對損耗影響變得很敏感，它們的精度較低。相較于它們，相干態在此時具有一定的優勢，它的精度也高于其他三者。損耗情況下，經典的相干態在平均粒子數較小時，比一些非經典量子態具有一定的優勢。

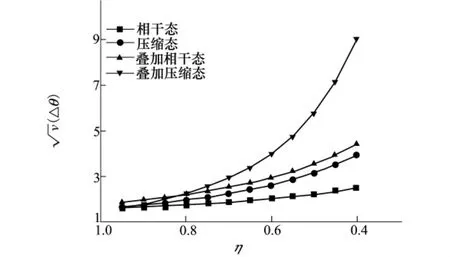
圖3　有損信道對各量子態精度影響(平均粒子數=0. 1)

4　結論

本文研究了無損與有損情況下，疊加相干態與疊加壓縮態的最優相位精度。利用分束器建立了一個信道損耗模型，根據此模型計算了2種量子態的精度。研究顯示各態受損耗的影響，精度均有所下降。當平均粒子數較大或較小時，其精度變化有所不同:

1)當各態平均粒子數較大時，壓縮態和相干態分別與其疊加形式精度相同。在一定損耗范圍內，壓縮態與疊加壓縮態精度較高。

2)當各態平均粒子數較小時，隨著損耗的增加，疊加壓縮態對外界環境的影響顯得很敏感，其精度衰減的更快些。此時經典的相干態精度最高。

參考文獻:

［1］Ospelkaus C，Warring U，Colombe Y，et al．Microwave Quantum Logic Gates for Trapped Ions［J］．Nature，2011，476: 181-184

［2］Sewell R J，Koschorreck M，Napolitano M，et al．Magnetic Sensitivity beyond the Projection Noise Limit by Spin Squeezing［J］．Phys Rev Lett，2012，109: 253605

［3］Higgins1 B L，Berry D W，Bartlett S D，et al．Demonstrating Heisenberg-Limited Unambiguous Phase Estimation without Adaptive Measurements［J］．New J Phys，2009，11: 073023

［4］Emilio Bagan，Alex Monras，Ramon Munoz-Tapia，et al．Phase Variance of Squeezed Vacuum States［J］．Phys Rev A，2008，78: 043829

［5］Lee Changwoo，Jeong H．Effects of Squeezing on Quantum Nonlocality of Superpositions of Coherent States［J］．Phys Rev A，2009，80: 052105

［6］Stobińska M，Jeong H，Ralph T C．Violation of Bell's Inequality Using Classical Measurements and Nonlinear Local Operations ［J］．Phys Rev A，2007，75: 052105

［7］Ourjoumtsev Alexei，Tualle-Brouri Rosa，Laurat Julien，et al．Generating Optical Schr?dinger Kittens for Quantum Information Processing［J］．Science，2006，312(5770) : 83-86

［8］Ourjoumtsev Alexei，Jeong Hyunseok，Tualle-Brouri Rosa，et al．Generation of Optical Schr?dinger Cats from Photon Number States［J］．Nature，2007，448: 784-786

［10］Knysh S，Smelyanskiy V N，Durkin G A．Scaling Laws for Precision in Quantum Interferometry and the Bifurcation Landscape of the Optimal State［J］．Phys Rev A，2011，83: 021804

［11］Cooper J J，Dunningham J A．Towards Improved Interferometric Sensitivities in the Presence of Loss［J］．New Journal of Physics，2011，13(11) : 115003

［12］Helstrom C W．Quantum Detection and Estimation Theory［M］．Academic Press，New York，1976

［13］Vittorio Giovannetti，Seth Lloyd，Lorenzo Maccone．Advances in Quantum Metrology［J］．Nature Photonics，2011，5: 222-229

［14］Holevo A S．Covariant Measurements and Imprimitivity Systems［J］．Lect Notes Maths，1984，1055: 153-172

［15］Gradshteyn I S，Ryzhik I M．Table of Integrals，Series，and Products［M］．Massachusetts Academic Press，2007

［16］Animesh Datta，Lijian Zhang，Nicholas Thomas-Peter，et al．Quantum Metrology with Imperfect States and Detectors［J］．Phys Rev A，2011，83: 063836

［17］金玉明，薛興恒，顧新身，等．實用積分表［M］．合肥:中國科技大學出版社，2006 Jing Y M，Xue X H，Gu X S，et al．The Utility Table of Integrals［M］．Hefei: University of Science and Technology of China Press，2006 (in Chinese)

Phase Precision of Superposition of Coherent State and Superposition of Squeezed State

Xie Duan1Miao Ruixia1Zhao Jian2

(1．School of Electronic Engineering，Xi'an University of Posts and Telecommunications，Xi'an 710121，China 2．School of Information Science and Technology，Northwest University，Xi'an 710069，China)

Abstract:This paper studies optimal phase precision of superposition of coherent state and superposition of squeezed state using Cramér-Rao bound approach．The results show that precision of superposition of coherent state only achieves the standard quantum limit and precision of superposition of squeezed state achieves Heisenberg limit．Using a dissipation model，we find accuracies of two quantum states decrease with increasing loss degree(η)．We also introduce coherent state and squeezed state and compare accuracies of four quantum states．When mean particle number is bigger，phase precisions of squeezed state and superposition of squeezed state are higher．When mean particle number is smaller，with the increasing loss of particle，phase precision of superposition of squeezed state decreases much faster as it is more susceptible to the environment．

Key words:phase precision，superposition of coherent state，superposition of squeezed state，dissipative channel，Cramer-Rao bounds，errors，estimation，normal distribution，optimization，photons，Poisson distribution，probability，Cramer-Rao lower bound method，dissipation analysis of superposition of squeezed states，dissipation channel，effect of dissipation channel on precision of each quantum state，mean particles number，phase precision，photon dissipation model，precision estimation of superposition of coherent states，precision estimation of superposition of squeezed states

作者簡介:謝端(1979—)，西安郵電大學講師，主要從事量子信息及微電子研究。

收稿日期:2014-11-04基金項目:國家自然科學基金(51302215)與陜西省教育廳科學研究計劃項目(14JK1682)資助

文章編號:1000-2758(2015) 02-0302-07

文獻標志碼:A

中圖分類號:O431．1