高速鐵路無砟軌道簡支槽型梁靜載彎曲試驗研究

王起才，薛彥瑾，張戎令，劉正楠，何志剛，王 沖

(1. 蘭州交通大學土木工程學院，甘肅 蘭州 730070；2. 道路工程災害防治技術國家地方聯合工程實驗室，甘肅 蘭州 730070)

預應力混凝土槽型梁是一種新型橋梁結構，由道床板、主梁及端橫梁等部分組成，適用于公路、鐵路橋梁及城市軌道交通建設[1]．槽型梁橋屬下承式開口薄壁結構[2]，與普通橋梁相比，主要有以下優點[3-8]：利用底板支承軌道及列車，降低軌道標高，在滿足橋下凈空的前提下顯著降低結構建筑高度；結構高度減薄，高跨比減小，結構體量較小，顯得輕巧、美觀；主梁腹板將隔音屏障功能與結構受力功能合二為一，節省了隔音板并抑制了噪音的傳播；主梁還可作為擋板，防止車輛傾覆；與同跨度的鋼梁相比，可節省鋼材且抗震性能優越，因此槽型梁適用于高速鐵路與城市軌道交通橋梁．由于槽型梁具有比較明顯的優點，所以各國都對這種橋梁做了相關研究，并建造了各種類型的槽型梁橋[9-10]．

目前，國內外許多專家對槽型梁的靜力行為進行了相關研究．聶建國等[11]在簡支槽形梁考慮空間受力的理論解中綜合考慮了槽形梁在整體彎曲、局部彎曲、 剪力滯效應和主梁扭轉作用的基礎上，用勢能駐值原理導出了簡支槽形梁在均布荷載作用下的解析解．戴公連[12]以滬昆高鐵某獨塔斜拉橋為研究對象，將模型試驗與數值模擬相結合，研究了槽形截面斜拉橋的塔梁固接結構模型的試驗方法、受力狀態、極限承載能力以及傳力機理等．段敬民[13]綜合考慮了槽形梁的剪切變形和剪滯翹曲應力的自平衡條件，以最小勢能原理為基礎建立了槽形結構三個廣義位移的控制微分方程和自然邊界條件，獲得了相應廣義位移的閉合解，并提出了一種對槽形梁靜力學特性的準確分析方法．田楊[14]分析了一跨雙線鐵路曲線簡支槽形梁，發現曲線槽形梁的受力呈現明顯的空間特性，并且在豎向荷載作用下，曲線外側主梁下緣承受的拉力較大，曲線內側相對較小，道床板的剪力滯現象也比較顯著．

盡管各專家對槽型梁在荷載作用下的力學特性研究較多，但對槽型梁實橋的靜載彎曲試驗卻研究較少．為此，本文對高鐵無砟軌道16 m后張法預應力混凝土槽型梁進行1:1模型靜載彎曲試驗，該研究成果可為高速鐵路無砟軌道預應力混凝土槽型梁橋的設計和安全運營提供一定的技術參考．

1 試驗概況

1.1 構件設計及材料性能

試驗梁為蘭新高鐵無砟軌道16m后張法全預應力混凝土等高度簡支槽形梁，截面幾何尺寸如圖1所示．橋梁全長16 500 mm，計算跨度15 900 mm，高2 000 mm，寬6 380 mm，跨中道床板厚450 mm，距梁右側2 205 mm處設φ100泄水孔，梁體設2%坡度，為防止發生次生破壞（非結構性破壞），對支座處兩端混凝土做加厚處理，其厚度為800 mm，槽形梁其他設計參數見表1．

1.2 試驗方法

根據《預應力混凝土鐵路橋簡支梁靜載彎曲試驗方法及評定標準》（TB/T2092－2003）[15]，縱向采用三點等效靜力集中荷載模擬活載，跨中設一集中荷載，其余兩個荷載左右對稱布置，各荷載縱向間距均為4 m，橫向采用四點靜力加載，兩個集中荷載作用在道床板上，距線路中心線兩側各717.5 mm，對稱線路中心線布置，另外兩個集中力作用在腹板中線上．各加載點采用油壓千斤頂，由油壓表讀數確定各級加載值的大小．試驗梁橫向加載如圖2所示，腹板加載如圖3所示．

圖1 槽型梁橫斷面圖 單位（mm）Fig.1 Cross section of the groove beam unit (mm)

表1 試驗梁設計參數Tab.1 Test beam design parameters

圖2 試驗梁橫向加載圖Fig.2 Test transverse load diagram

圖3 試驗梁腹板加載圖Fig.3 Test beam web loading diagram

1.3 加載程序及測點布置

靜載彎曲試驗加載程序分兩階段進行，預加載階段（第一循環加載）和正式加載階段（第二循環加載）．預加載和正式加載均采用分級加載，每級加載值不大于開裂加載量理論值的10%，加載完成后持荷持續一定時間， 然后記錄本級荷載下的結構響應．當總荷載加至理論開裂荷載的80%時，對加載分級進行加密，進一步減小每級荷載增量，以準確捕捉開裂荷載．預加載的目的是檢驗整個試驗裝置的可靠性、安全性及消除試驗裝置和梁體的非彈性變形．預加載值不宜超過梁體開裂試驗荷載計算值的80%．第二循環加載等級及加載時間見表2所示．

在試驗梁跨中底板沿橫向等間距布置4個撓度測點，在南側及北側腹板跨中各布置一個撓度測點．在梁體底板中心線下側鋼筋中布置鋼筋應變測點MSZ-1，在底板上表面距梁體中心線2 390 mm處左右各對稱布置鋼筋應變測點，分別為MSZ-2和MSZ-3．在槽型梁跨中截面布置混凝土應變測點，圖4為梁體跨中截面混凝土應變測點布置立面圖，圖5為梁體跨中截面混凝土應變測點布置平面圖，其中“M”表示跨中截面，“H”表示橫向應變測點，“Z”表示縱向應變測點．

圖4 梁體跨中截面混凝土應變測點布置立面圖Fig.4 Vertical section of the concrete strain gauge in the cross section of beam

圖5 混凝土應變測點布置平面圖Fig.5 The layout plan of concrete strain gauge

表2 第二循環加載Tab.2 Second cyclic loading

2 結果與討論

2.1 主要試驗現象

試驗加載前，用40倍放大鏡在梁體兩側跨中8 m區段下翼緣及梁底面仔細查找裂紋．對初始裂紋（表面收縮裂紋及表面損傷裂紋）及局部缺陷，用藍色鉛筆標記．第一循環加載結束時，梁體除初始裂縫外，其跨中底板、南側腹板及北側腹板均未出現明顯的橫向裂縫和縱向裂縫．第二循環加載時，當加載到1.05級時，梁體底板、底板和腹板交界處出現縱向裂縫，隨著荷載的增大，底板和腹板處的縱向裂縫沿斜向延伸，裂縫的寬度在逐漸增大，且裂縫的條數也在增多．當加載結束時，在底板與腹板低交界處出現4條縱向裂縫，其裂縫最長達3.6 cm，最寬為0.1 mm，在底板跨中出現兩條縱向裂縫，最長為14 cm，最寬為0.16 mm，梁體跨中底板千斤頂作用位置處也出現了縱向裂紋，梁體跨中底板、南側腹板及北側腹板未出現明顯的受力橫向裂紋．加載到1.2級時，將槽型梁混凝土各部分展開，其裂縫分布的俯視圖如圖6所示．表3為第二循環加載荷載值．

圖6 槽型梁混凝土裂縫分布展開圖Fig.6 Groove beam concrete cracks distribution diagram

表3 第二循環加載荷載值(kN)Tab.3 Second cyclic loading load value (kN)

2.2 荷載-位移曲線

圖7 槽型梁跨中彎矩-撓度曲線Fig.7 Shaped beam span moment-deflection curve

圖7為槽型梁跨中彎矩-撓度曲線．當加載等級小于0.8級時，彎矩-撓度曲線基本呈直線，即槽型梁各截面的應力水平較低，遠未達到屈服．此后，隨著加載等級的提高，曲線逐漸彎曲，斜率減小，表明梁的剛度有一定程度的降低．隨著荷載的增加，梁底板跨中的撓度在逐漸增大，梁的剛度也在顯降低，當加載等級為1.2級時，梁底板跨中撓度達到最大值4.1 mm．當槽型梁在靜活載作用下時，其撓度值為1.6 mm，滿足ψf實測＜1.05f設計的要求，即靜載試驗時梁體的剛度滿足要求．

圖8 腹板荷載-跨中撓度Fig.8 Web load - span deflection

圖8為第二循環加載過程中，南、北兩側腹板荷載-跨中撓度曲線．隨著腹板荷載的增加，南側腹板跨中和北側腹板跨中的撓度值都在增加．在加載初始階段，由于梁體受自重、二期恒載等作用，其南、北兩側腹板跨中都出現不同程度的撓度，其中南側腹板跨中撓度值為0.39 mm，北側腹板跨中撓度值為0.61 mm，即北側腹板撓度是南側腹板撓度的1.56倍．隨著加載等級的提高，北側腹板跨中撓度的增長趨勢大于南側腹板跨中撓度的增長趨勢，并且在相同的荷載情況下，北側腹板跨中撓度值始終大于南側腹板跨中撓度值，且隨著荷載的增大，兩者撓度的差值也越來越大．這是因為對梁體進行加載時，底板采用非對稱加載，使得底板承受的荷載主要偏向于北側腹板，故北側腹板撓度始終大于南側腹板撓度．當荷載為318.7 kN時，南、北兩側腹板跨中撓度達到最大值，分別為4.53 mm和5.54 mm，即北側腹板撓度是南側腹板撓度的1.2倍．

圖9 腹板荷載-支座沉降曲線Fig.9 Web load - bearing settlement curve

從圖9可見，隨著腹板荷載的增加，東、西兩側支座均出現不同程度的沉降．當腹板荷載在0～68.7 kN時，東、西兩側的支座沉降值基本相同．荷載在152.3 kN時，東側支座沉降值發生突變，且比西側支座沉降值要大，造成這一現象的主要原因是東、西兩側加載千斤頂的不一致性．當試驗荷載在318.7 kN時，東、西側支座沉降達到最大值，分別為1.30 mm和1.18 mm，從整個試驗過程來看，雖然東、西兩側支座沉降不同，但沉降的差值很小，最大差值也僅為0.19 mm，所以可認為東、西側支座沉降不會對結構產生影響．

2.3 荷載-應力曲線

槽型梁加載到1.2級時跨中截面混凝土應力實測結果（不包含自重的影響）見表4．從表4可見跨中截面混凝土橫向最大應力為4.62 MPa，最小應力為-4.54 MPa；跨中截面混凝土縱向最大應力為12.46 MPa，最小應力為-5.04 MPa．

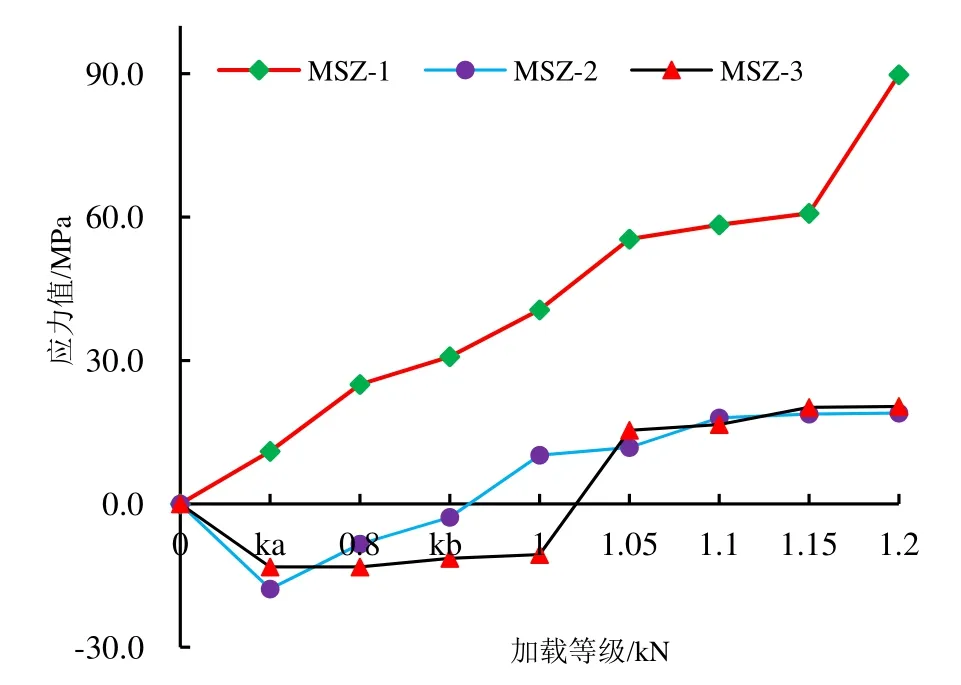
圖10 荷載-鋼筋應力曲線Fig.10 Load - reinforced stress curve

如圖10所示，隨著加載等級的增加，MSZ-1處的鋼筋應力值也在增大，當加載等級在0-1.05級時，MSZ-1處的鋼筋應力值的增長幅度較快，當加載等級為1.05級時，MSZ-1處的鋼筋應力發生突變，且突變后的應力值隨加載等級的增加其增長幅度較緩，即加載等級在1.05～1.15之間時，MSZ-1處的鋼筋應力值的變化很小．當加載等級在1.15級時，MSZ-1處的鋼筋應力值發生急劇突變，突變后的應力值隨加載等級的增加增長幅度很大，在加載等級為1.2時，MSZ-1處的鋼筋應力值達到最大，其值為89.8 MPa．即整個試驗過程中MSZ-1處受拉鋼筋的應力變化由彈性階段、屈服階段和強化階段組成．當加載等級在0～ka級時，MSZ-2和MSZ-3處的鋼筋應力處于受壓狀態，且MSZ-2處的鋼筋應力值大于MSZ-3處的鋼筋應力值，當加載等級在ka級時，MSZ-2和MSZ-3處的鋼筋應力發生突變．當加載等級為ka～1.0級時，MSZ-2處的鋼筋應力值隨加載等級的增大在減小，且MSZ-2處的鋼筋應力值在這個加載過程中由受壓狀態變為受拉狀態，而MSZ-3處的鋼筋應力值隨加載等級的增大其值沒有發生很大變化，仍處于受壓狀態．當加載等級在1.0～1.05級時，MSZ-3處的鋼筋應力值由受壓狀態變為受拉狀態．當加載等級在1.05～1.2級時，MSZ-2和MSZ-3處的鋼筋應力隨加載等級的增大，應力值也在增大，但增長幅度較緩，在1.2級時達到最大值，分別為19.0 MPa和20.4 MPa．由于MSZ-2和MSZ-3對稱梁體中心線布置，出現上述情況的原因是加載位置不同和槽型梁的空間受力特性所引起的．

表4 靜載彎曲試驗跨中混凝土應力值(MPa)Tab.4 Static load bending stress test span concrete (MPa)

3 結論

通過對高速鐵路無砟軌道16 m后張法預應力混凝土簡支槽型梁的靜載彎曲試驗，獲取了該橋梁的裂縫發展規律、變形特性、支座沉降、應力發展規律，通過對這些結果的分析得出如下主要結論：

(1) 槽型梁在靜載試驗結束后，其裂縫寬度、剛度、抗裂情況和預應力度滿足試驗要求．

(2) 當加載等級為1.2級時，MSZ-1處鋼筋應力達到最大為89.8 MPa，且整個試驗過程中，MSZ-1處鋼筋應力變化符合平截面假定，而MSZ-2和MSZ-3在整個過程中先處于受壓狀態后處于受拉狀態，表現出一定的空間受力特性．

(3) 本試驗是國內進行的大規模實橋靜載彎曲試驗，而對于高速鐵路無砟軌道16 m后張法預應力混凝土簡支槽型梁的靜載彎曲試驗研究，目前在國內尚未見相關報道，因此該研究成果可為此類橋梁設計和安全運營提供一定的技術參考 ．

References

[1] 胥為捷, 薛偉辰. 預應力混凝土槽型梁的研究與應用[J]. 建筑結構, 2006, 36(S1): 100-105.XU Weijie, XUE Weichen. Research and applications of prestressed U-shaped concrete girder[J]. Journal of Building Structure, 2006, 36(S1): 100-105.

[2] 黃僑, 陳卓異, 楊明. 槽型梁橋力學性能的研究現狀與展望[J]. 中外公路, 2013, 33(6): 131-135.HUAN Qiao, CHEN Zhouyi, YANG Ming. Groove mechanical properties research Status and Prospects beam bridge[J]. Journal of China & Foreign Highway, 2013,33(6): 131-135.

[3] 胡匡璋, 江新元, 陸光閭. 槽形梁[M]. 北京: 中國鐵道出版社, 1987.HU Kuangzhang, JIANG Xinyuan, LU Guanglü. Trough girder[M]. Beijing: China Railway Press, 1987.

[4] 張士鐸. 箱型薄壁梁剪力滯效應[M]. 北京: 人民交通出版社, 1998.ZHANG Shiduo. Shear lag effect of box type thin walled beams[M]. Beijing: People's Communications Press,1998.

[5] 賀恩懷. 槽型梁在城市軌道交通工程中的應用[J]. 鐵道工程學報, 2003(2): 13-16.HE Enhuai. Application of channel girders in project of urban rail transit[J]. Journal of Railway Engineering Society, 2003(2): 13-16.

[6] SHEPHERD B, GIBBENS B. The evolution of the concrete channel bridge system and its application to road and rail bridges[C]//Concrete Structures: the Challenge of Creativity, CEB-FIB Symposium. France, Avignon, 2004.

[7] SONG Q, SCORDELIS A C. Formulas for shear-lag effect of T-, I- and box beams[J]. J. Struct. Engrg., ASCE,1990, 116(5): 1306-1318.

[8] 陸光閭. 連續鐵路槽形梁橋空間作用分析[J]. 鐵道學報, 2000, 22(S1): 41-46.LU Guanglü. Spatial analysis of railway continuous through girder bridge[J]. Journal of the china railway society, 2000, 22(S1): 41-46.

[9] Japan Prestressed Concrete Engineering Association.Prestressed Concrete in Japan[M]. Tokyo: Kadokawa Shoten Publishing Co. Ltd., 1990.

[10] Guglielmetti U. Swiss autoroute N9-bridges over the Rhine at Riddes[Z]. FIP Notes, 1990.

[11] 聶建國, 胡紅松. 簡支槽形梁考慮空間受力的理論解[J]. 工程力學, 2012, 29(12): 64-71.NIE Jianguo, HU Hong-song. Theoretical solution of simple supported trough girder considering spatial effect[J]. Engineering Mechanics, 2012, 29(12): 64-71.

[12] 戴公連, 粟 淼. 高鐵槽形梁斜拉橋塔梁固接結構試驗研究及數值分析[J]. 鐵道學報, 2015, 37(3): 85-92.DAI Gonglian, SU Miao. Experimental study and numerical analysis on pylon-girder rigid fixity structure of a trough girder cable-stayed bridge in high-speed railway[J]. Journal of the china railway society, 2015, 37(3):85-92.

[13] 段敬民, 錢永久. 槽形截面梁靜力學特性的研究[J].工程力學, 2010, 27(9): 128-132.DUAN Jingmin, QIAN Yongjiu. Study on static characteristic of u-shape beams[J]. Engineering Mechanics,2010, 27(9): 128-132.

[14] 田 楊, 鄧運清, 黃勝前. 雙線鐵路曲線簡支槽形梁的空間分析[J]. 鐵道工程學報, 2012,(3): 24-28.TIAN Yang, DENG Yunqing, Huang Sheng qian. The spatial anlysis of curved simple trough girder with two-lane railway[J]Journal of Railway Engineering Society, 2012( 2 ): 24-28.

[15] 中華人民共和國鐵道部. 預應力混凝土鐵路橋簡支梁靜載彎曲試驗方法及評定標準: TB/T 2092-2003[S]. 北京: 中國標準出版社, 2003.Ministry of Railways of the People's Republic of China.Post-tensioned pre-cast concrete simple-supported girder for railway bridge pro-stress: TB/T 2092-2003[S]. Beijing: China Standard Press, 2003.