非均勻三次B樣條曲線插值的GS-PIA算法
劉曉艷,鄧重陽
(杭州電子科技大學理學院,浙江 杭州 310018)
摘要:提出了非均勻三次B樣條曲線插值的GS-PIA算法。該算法與解線性方程組的高斯-賽德爾迭代法有同樣的優點,即把已經更新的點參與到迭代過程來優化迭代過程;同時也具有漸進迭代逼近方法的優點,即有明確的幾何意義,并能得到一系列逐次逼近插值點的非均勻三次B樣條曲線。
關鍵詞:非均勻三次B樣條;迭代算法;漸進逼近
DOI: 10.13954/j.cnki.hdu.2015.02.019
非均勻三次B樣條曲線插值的GS-PIA算法
劉曉艷,鄧重陽
(杭州電子科技大學理學院,浙江 杭州 310018)
摘要:提出了非均勻三次B樣條曲線插值的GS-PIA算法。該算法與解線性方程組的高斯-賽德爾迭代法有同樣的優點,即把已經更新的點參與到迭代過程來優化迭代過程;同時也具有漸進迭代逼近方法的優點,即有明確的幾何意義,并能得到一系列逐次逼近插值點的非均勻三次B樣條曲線。
關鍵詞:非均勻三次B樣條;迭代算法;漸進逼近
DOI:10.13954/j.cnki.hdu.2015.02.019
收稿日期:2014-06-16
基金項目:國家自然科學基金資助項目(61003194,61370166)
通信作者:
作者簡介:劉曉艷(1989-),女,河南泌陽人,在讀研究生,計算機圖形學.鄧重陽副教授,E-mail: dcy@hdu.edu.cn.
中圖分類號:O242
文獻標識碼:A
文章編號:1001-9146(2015)02-0079-04
Abstract:This paper presents a non-uniform cubic B-spline curve interpolation algorithm of GS-PIA. The algorithm and the Gauss-Seidel iterative method of solving linear equations have the same advantages, namely the points involved in the iterative process which has been updated to optimize the iterative process. At the same time, the algorithm also has the advantage of progressive iterative approximation method, namely, there is a clear geometric significance, and can make a series of non-uniform cubic B-spline curve approximation interpolation points.
0引言
數據擬合是求解現實世界中科學與工程問題的基本工具之一。漸進迭代逼近(Progressive Iteration Approximation,PIA)是一種將數據點擬合成為曲線或曲面的技術。文獻[1]在研究樣條擬合問題時,就基于盈虧修正思想提出了均勻三次B樣條曲線的幾何迭代算法。文獻[2]在一次學術交流討論會中也闡述了這一思想。文獻[3]證明了對于非均勻三次B樣條曲線和曲面同樣具有PIA性質。文獻[4]將PIA推廣到了擁有歸一化全正基函數的混合曲線、曲面中。文獻[5]證明了有理B樣條曲線曲面同樣具有這個PIA性質。文獻[6]比較了不同種類基函數的選取對于收斂速度的影響,并且證明了B樣條基函數不僅具有保形和PIA性質,而且具有最快的收斂速度。文獻[7]設計了一種PIA方法,本質上來說就是均勻周期三次B樣條的PIA方法。文獻[8]設計了一種帶權值的PIA來加快擬合的收斂速度。文獻[9]發現了PIA的局部性質,即漸進迭代逼近可以為每一個數據點分別設定擬合精度。文獻[10]通過變換矩陣,提出了一種可以統一傳統PIA方法、帶權值的PIA方法和局部PIA方法的擴展方法。最近,文獻[11]進一步提出了LSPIA,即基于PIA的B樣條曲線曲面最小二乘擬合方法。
在考察PIA方法與解線性方程組的經典迭代法之間的聯系時本文筆者發現,如果每次迭代時把已經更新的點參與到迭代過程中去,高斯-賽德爾(Gauss-Seidel,GS)迭代法也可以看作是一種PIA方法,本文稱之為GS-PIA方法。數值算例表明,非均勻三次B樣條曲線插值的GS-PIA方法是收斂的,而且比以前PIA方法的存儲量更少,收斂速度也更快。
1GS-PIA算法
1.1 PIA算法的導出
文獻[3]中給出了非均勻三次B樣條曲線曲面的漸進迭代逼近算法,并證明了這種算法的收斂性。其中非均勻B樣條曲線的漸進迭代逼近算法的具體流程如下。

1.2 GS迭代法
設有線性方程組Ax=b,即:

(1)

1.3 GS-PIA算法的導出

仿照首次迭代知k次迭代后有:

(2)
第j個控制點的第k+1次調整量為:
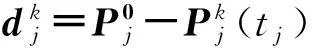
(3)
得到k+1次迭代需要的第j個控制點:

(4)
那么,第k+1次迭代后的一條非均勻三次B樣條曲線為:



(5)
文獻[3]提出的PIA算法如下:

(6)
通過比較式(5)和式(6)可知,本文提出的GS-PIA算法的迭代格式中,k層少了一項,因此GS-PIA算法存儲量更少。
2數值實例


圖1 采用GS-PIA算法插值三葉玫瑰線上的采樣點

表1 兩種PIA算法插值三葉玫瑰線上的采樣點的誤差
3結束語
本文提出了用于非均勻三次B樣條曲線插值的GS-PIA算法,數值算例表明,GS-PIA算法是收斂的,且收斂速度較快,優于原來的PIA算法。同時該算法存儲更少。但是算法的收斂性如何證明,以及對于更高次的非均勻B樣條曲線插值,類似的GS-PIA算法是否收斂,收斂速度如何都是值得繼續探討的問題。
參考文獻
[1]齊東旭,田自賢,張玉心,等.曲線擬合的數值磨光方法[J].數學學報,1975,18(3):173-184.
[2]De Boor C. How does Agee’s smoothing method work[C]//Proceedings of the 1979 army numerical analysis and computers conference, ARO Report 1979:299-302.
[3]Lin H W, Wang G J, Dong C S. Constructing iterative non-uniform B-spline curve and surface to fit data points[J]. Science in China Series: Information Sciences,2004.47(3):315-331.
[4]Lin H W, Bao H J, Wang G J. Totally positive bases and progressive iteration approximation[J]. Computers & Mathematics with Applications,2005.50(3):575-586.
[5]Shi L, Wang R. An iterative algorithm of NURBS interpolation and approximation[J]. Journal of Mathematical Research and Exposition,2006,26(4):735-743.
[6]Delgado J, Pea J M. Progressive iterative approximation and bases with the fastest convergence rates[J]. Computer Aided Geometric Design,2007,24(1):10-18.
[7]Martin T, Cohen E, Kirby RM. Volumetric parameterization and trivariate B-spline fitting using harmonic function[J]. Computer Aided Geometric Design,2009,26(6):648-664.
[8]Lu L Z. Weighted progressive iteration approximation and convergence analysis[J]. Computer Aided Geometric Design,2010,27(2):129-137.
[9]Lin H W. Local progressive-iterative approximation format for blending curves and patches[J]. Computer Aided Geometric Design,2010,27(4):322-339.
[10]Deng S H, Guan S J, Wang G Z,et al. An Extension of a New Kind of Graphics Fitting Method[J]. Applied Mathematics & Information Sciences,2013,7(2):741-747.
[11]Deng C Y, Lin H W. Progressive and iterative approximation for least squares B-spline curve and surface fitting[J]. Computer-Aided Design,2014,47(1):32-44.
Non-uniform Cubic B-spline Curve Interpolation Algorithm of GS-PIA
Liu Xiaoyan, Deng Chongyang
(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Key words: non-uniform cubic B-spline curve; iterative algorithm; progressive approximation

