指數型分布粗糙地面寬帶后向電磁散射的FDTD研究

武劍,任新成,朱小敏

(延安大學物理與電子信息學院，陜西 延安 716000)

?

指數型分布粗糙地面寬帶后向電磁散射的FDTD研究

武劍,任新成,朱小敏

(延安大學物理與電子信息學院，陜西 延安 716000)

摘要：采用蒙特卡羅方法模擬生成指數型分布粗糙地面，運用時域有限差分方法(FDTD)研究了高斯脈沖波入射時粗糙地面的寬帶電磁散射問題。通過數值計算得到不同頻率響應對應的后向散射系數，分析了粗糙地面相關長度、高度起伏均方根、土壤濕度和入射角的變化對后向散射系數的影響，得到了指數型分布粗糙地面的寬帶后向電磁散射特性。

關鍵詞：電磁散射；FDTD； 粗糙地面；后向散射系數；高斯脈沖波

隨著無線通信技術的不斷發展，隨機粗糙面電磁散射問題日漸成為至關重要的研究課題，廣泛應用于微波遙感、風場反演和超寬帶雷達探測等諸多領域。目前，單頻電磁波入射粗糙面時的電磁散射問題的研究已經取得了一些進展，任新成等[1]在粗糙地面與上方目標復合電磁散射研究中，利用時諧場源入射并外推至遠區場；張連波等[2]應用矩量法，采用脈沖基函數結合點匹配技術研究了三層粗糙面的散射系數；Wang等[3]用混合方法研究了粗糙面與上方目標的復合電磁散射特性；Sultan-Salem等[4]利用基爾霍夫近似研究了分形粗糙面的電磁散射特性。對于脈沖波入射時的粗糙面寬帶(超寬帶)電磁散射問題的研究則相對較少[5-6]。但是，實際上粗糙面寬帶電磁散射對于超寬帶雷達目標成像、叢林透視和低雷達截面(RCS)目標探測的研究[7]，以及超寬帶無線通信技術的發展[8]等都具有重要的借鑒意義和實用價值。

粗糙面寬帶電磁散射問題傳統上是通過近似解析方法進行研究的。但是，近似解析方法大多限于求解單次散射，實現起來較為簡單，但有一定的適用范圍。隨著研究的進一步深入，矩量法[2]、前后向迭代算法[9]、有限元法[10]和時域有限差分方法(FDTD)[11]等數值算法得到快速發展。FDTD由Yee于1966年首次提出[12-13]，與其他數值方法相比，不僅能節省計算機內存，而且具有CPU占用時間短、計算效率高等優點，因此受到廣泛的關注。

本文采用指數型分布粗糙面模擬實際地面，地面土壤介電常數利用Wang等[14]的四成分模型，運用FDTD方法對高斯脈沖波入射下的粗糙地面進行時域散射研究，所得散射場數據由瞬態場外推后再經傅里葉變換獲得頻域信息，得到后向散射系數隨頻率的變化曲線，分析了粗糙地面相關長度、高度起伏均方根，土壤濕度和入射角的變化對后向散射系數的影響，得到了指數型分布粗糙地面的寬帶后向電磁散射特性。

1粗糙地面模擬與散射模型

1.1粗糙地面模擬

在自然界中，實際地物表面、海面均可看作是二維隨機粗糙面。為了便于研究，可以將坐標系中一個方向變化另一個方向不變的二維模型簡化為一維模型。對于一維粗糙面的研究，同樣具有理論意義和實際意義。

用蒙特卡羅方法可以模擬生成一維隨機粗糙面[15]。蒙特卡羅方法又稱線性濾波法，即在頻域用功率譜對其濾波再作逆快速傅里葉變換得到粗糙面的高度起伏。長度為L的一維粗糙面可以由下式生成

(1)

式中，xn=nΔx(n=-N/2+1,…,N/2)表示粗糙面上第n個采樣點，Δx為采樣間隔；kj=2πj/L，表示離散波數；F(kj)為f(xn)的傅里葉變換，可由下式計算

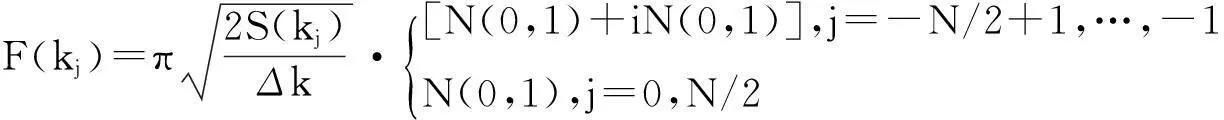
(2)

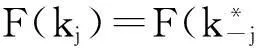
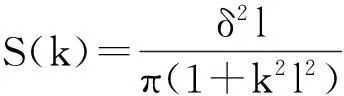
(3)

式中，δ、l分別為粗糙面高度起伏均方根、相關長度，k為波數。

1.2散射模型

圖1為一維隨機粗糙面電磁散射的幾何示意圖，粗糙面由蒙特卡羅方法模擬生成，x軸上方為自由空間，下方為均勻土壤介質。圖2為粗糙面電磁散射的FDTD模型。總場邊界(TF/SF邊界)為平面，上方為散射場區，下方為總場區，在總場邊界設置等效電磁流引入入射波，在散射場區設置輸出邊界，從而外推至遠區散射場。在FDTD計算區域外設置厚度為10個網格的各向異性介質完全匹配層(UPML)吸收邊界。

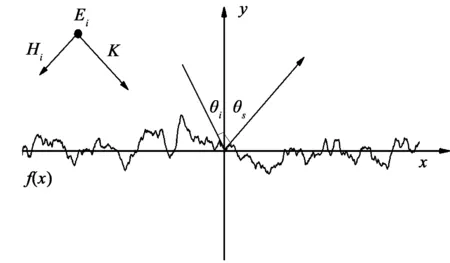
圖1　一維粗糙面散射幾何示意圖Fig.1　　Geometry llustration of electromagnetic　scattering of 1D rough surface

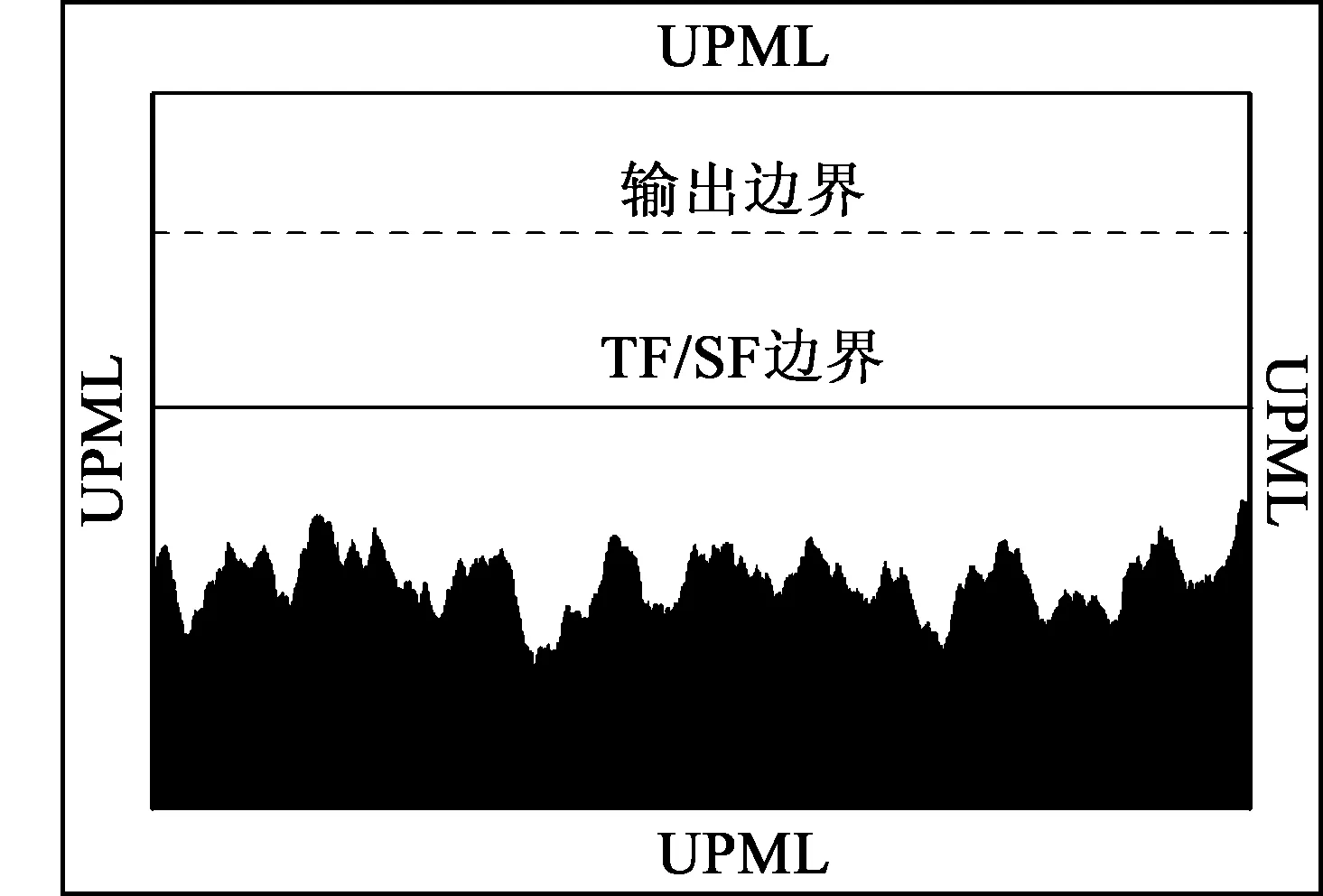
圖2　粗糙面散射FDTD模型Fig.2　　FDTD computation model for rough 　surface scattering

2FDTD方法

對于二維問題，電磁波分為TE波和TM波。以TE波為例，FDTD差分公式為：

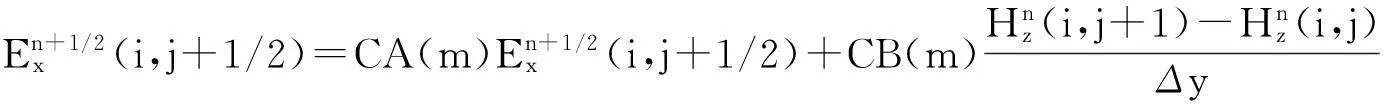
(4)

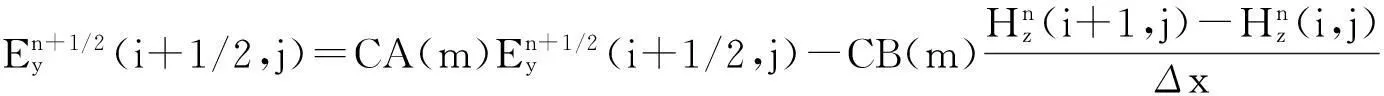
(5)

(6)

(4) ～ (6)式中CA(m)、CB(m)、CP(m)、CQ(m)及m的取值見文獻[13]。Δx、Δy分別為FDTD區域x、y方向的離散網格寬度。同理，根據TE和TM波之間的對偶關系，可寫出TM波的FDTD差分公式。

根據等效原理，設置等效電磁流，將入射波引入總場區，而散射場區沒有入射波。文獻[16]選取了微分高斯脈沖波為入射波，而本文選取高斯脈沖波為入射波，其表達式為

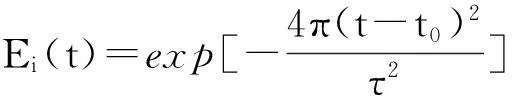
(7)

式中τ為常數，決定高斯脈沖的寬度。本文取τ=2/f，此時頻譜為最大值的4.3%，選用高斯脈沖波使得t0=0.8τ時，脈沖在起始時刻近似為0。

為了解決截斷邊界處場值突變而產生的反射問題，普遍給入射波附加平滑高斯窗函數

G(x,y)=exp{-[(x-x0)2+(y-y0)2](cosθi/T)2},

(8)

式中θi為入射角,取x0=y0=0。τm應滿足以下條件

exp[-(ρmcosθ/T)2]=10-3，

(9)

則T=ρmcosθ/2.6，ρm為中心到邊緣的最小距離。

由于FDTD不能直接計算電磁散射無限區域數據，因此需在截斷邊界設置吸收邊界條件模擬開域電磁散射過程。本文選取UPML吸收邊界，取10個網格厚度。以TE波為例，各向異性介質Maxwell旋度方程表示為

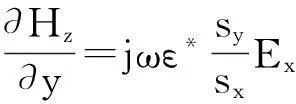
(10)

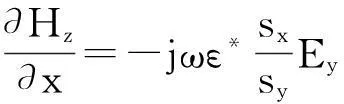
(11)

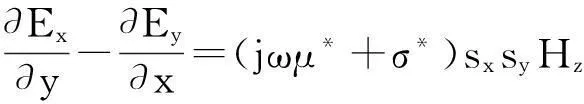
(12)

(10) ～ (12)中ε*、μ*、σ*代表與UPML層相鄰內部介質的電磁參數。sx和sy分別為x和y方向的單軸參數，具體形式見文獻[13]。

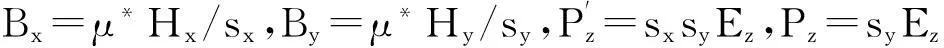
通過FDTD計算得到近場數據后，運用瞬態場外推方法可得到遠區散射場，再由傅里葉變換獲得遠區場的頻域形式。散射系數定義為

σ=10·log10(NRCS)，

(13)

單位為dB，式中NRCS表示歸一化雷達散射截面，具體形式為

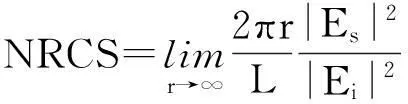
(14)

式中，r、Es、Ei分別表示觀察點到原點的距離、遠區散射場和入射波電場。

3數值計算結果與討論

用上述理論和數值方法計算了指數型分布粗糙地面的后向散射系數，討論了粗糙面相關長度、高度起伏均方根，土壤濕度以及入射角對后向散射系數的影響。具體數值計算中，選用TM極化高斯脈沖平面波作為入射波，FDTD的網格寬度為dx=0.5cm，粗糙面的抽樣長度為3 200個網格，選取50個粗糙面進行統計計算。如無特殊說明，取入射角θi=30°，土壤類型選擇粉沙壤土，土壤介電常數利用Wang等[14]的四成分模型進行計算。

3.1粗糙面相關長度對后向散射系數的影響

圖3為后向散射系數σ隨粗糙面相關長度l的變化關系。其中粗糙面高度起伏均方根δ=2cm，土壤介電常數εr=9.968 2-i3.055 6(土壤濕度取mv=0.2g/cm3)。由圖3可知，當入射波頻率f<75MHz時，后向散射系數σ先在較小的一個頻域內迅速增大，接著急劇減小，在75MHz附近取極小值，并且極小值隨著l的增大而增大，與文獻[16]相比，取得極小值的頻率位置略小于微分高斯脈沖波作為入射源時的頻率位置；當75375MHz時，σ隨f的增大振蕩地緩慢變化，且σ隨l的增大而減小，不同相關長度對應的σ相差不大。總之，在不同頻率范圍內，粗糙面相關長度對散射系數的影響不同。

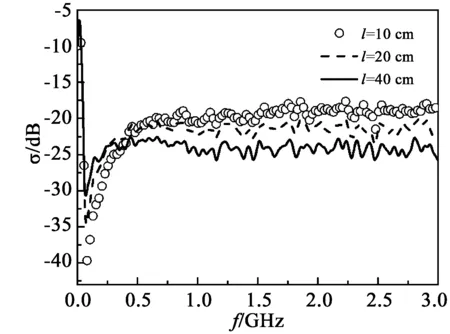
圖3　粗糙面相關長度對后向散射系數的影響Fig.3Impact of rough surface correlation length on backward scattering coefficient σ

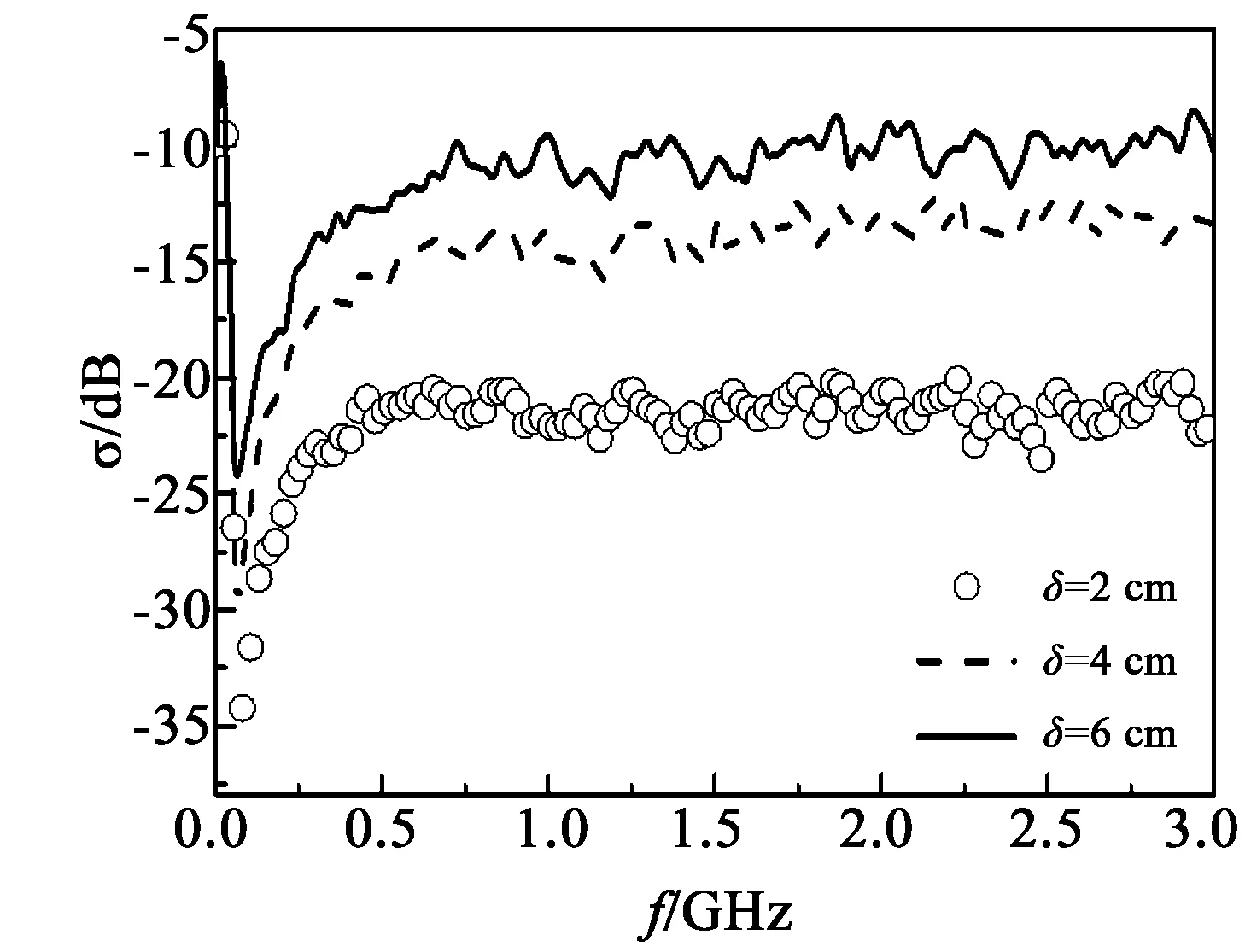
圖4　粗糙面均方根對后向散射系數的影響Fig.4Impact of height RMS of rough surface on backward scattering coefficient σ

3.2粗糙面高度起伏均方根對后向散射系數的影響

圖4為后向散射系數σ隨粗糙面高度起伏均方根δ的變化關系圖。計算中相關長度l=20cm，土壤介電常數εr=9.968 2-i3.055 6(土壤濕度mv=0.2g/cm3)。由圖4可知，當入射波頻率f<65MHz時，后向散射系數σ先在較小的一個頻域內迅速增大，接著急劇減小，在65MHz附近取極小值，并且極小值隨著δ的增大而增大；當65500MHz時，σ隨f的增大振蕩地緩慢變化，且σ隨δ的增大而增大，同一頻率不同δ對應的σ相差較大。經分析，由于粗糙面高度起伏均方根增大，粗糙面粗糙度增大，導致地面散射增強。

3.3土壤濕度對后向散射系數的影響

圖5為后向散射系數σ隨土壤濕度mv的變化關系圖。計算過程中取δ=2cm，相關長度l=20cm，土壤介電常數根據四成分模型進行計算，即εr1=4.851 2-i0.802 7(mv1=0.1g/cm3)，εr2=9.9682-i3.0556(mv2=0.2g/cm3)，εr3=25.052 7-i9.7835(mv3=0.4g/cm3)。由圖5可知，當入射波頻率f<75MHz時，σ先在較小的一個頻域內迅速增大，接著急劇減小，在75MHz附近取極小值，σ的極小值不隨mv的變化而變化；當75500MHz時，σ隨f的增大振蕩地緩慢變化，且σ隨mv的增大而增大，同一頻率不同mv對應的σ相差不大。經分析，這是由于土壤濕度增大使得土壤介電常數的實部快速增大，而導致地表面散射增強。

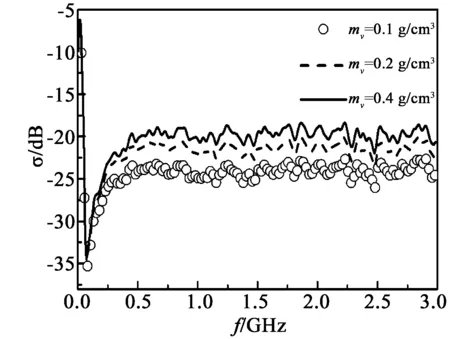
圖5　土壤濕度對后向散射系數的影響Fig.5　　Impact of soil moisture on backward　scattering coefficient σ

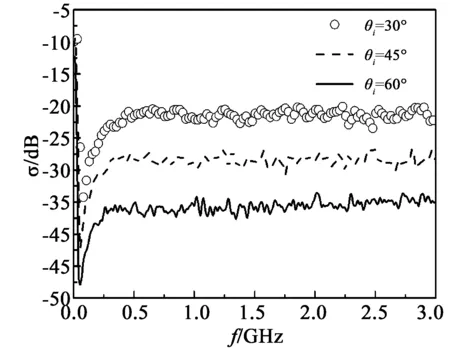
圖6　入射角對后向散射系數的影響Fig.6　　Impact of incident angle on backward 　scattering coefficient σ

3.4入射角對后向散射系數的影響

圖6為后向散射系數σ隨入射角θi的變化關系。其中取δ=2cm，l=20cm，土壤介電常數εr=9.968 2-i3.055 6(mv=0.2g/cm3)。由圖6可知，當入射波頻率f<55MHz時，后向散射系數σ先在較小的一個頻域內迅速增大，接著急劇減小，在55MHz附近取極小值，并且極小值隨著θi的增大而減小；當55500MHz時，σ隨f的增大振蕩地緩慢變化，且σ隨θi的增大而減小，同一頻率不同θi對應的σ相差較大。總之，入射角越大，地面散射越弱。

4結語

本文研究了高斯脈沖波入射指數型分布粗糙地面的寬帶電磁散射特性，運用FDTD瞬態場外推的方法進行研究，得出了粗糙地面高度起伏相關長度、均方根、土壤濕度及入射角等參數對后向散射系數的影響規律，結果表明后向散射系數隨各參數變化的規律比較明顯，但比較復雜；入射波波源不同，使得后向散射系數取得極值時的頻率位置和對應的極值也略有不同。當然，本文僅討論了一維指數型粗糙面的寬帶后向散射問題，計算結果還有待進一步的實驗驗證，對于其他分布的一維地物表面、二維地物表面等的前向散射問題還有待今后進一步地研究。

參考文獻：

[1]任新成，郭立新，焦永昌.雪層覆蓋的粗糙地面與上方矩形截面柱復合電磁散射的時域有限差分方法研究[J].物理學報，2012,61(14):144101.

[2]張連波，郭立新，茍雪銀，等.三層粗糙面電磁散射的矩量法研究[J].西安電子科技大學學報：自然科學版，2013,40(6):147-154.

[3]WANGR,GUOLX,MAJ.Hybridmethodforinvestigationofelectromagneticscatteringfromconductingtargetabovetherandomlyroughsurface[J].ChinesePhysicsB，2009,18(4):1503-1511.

[4]SULTAN-SALEMAK,LEONARTYLERG.Validityofthekirchhoffapproximationforelectromagneticwavescatteringfromfractalsurfaces[J].IEEEtrans.geosci.remoteSensing. 2004, 42(9):1860-1870.

[5]樊君，雷振亞，謝擁軍,等.半空間目標寬帶電磁散射特性的快速插值方法[J].電波科學學報，2012,27(1):84-89.

[6]黃紀軍，粟毅，計科峰,等.地面復雜目標寬帶電磁散射特性分析[J].微波學報，2005,21(2):8-11.

[7]曹秋生，劉賀軍，馬建超,等.基于超寬帶雷達的叢林目標探測無人機系統分析[J].中國電子科學研究院學報，2012,7(4):351-355.

[8]魏為民，唐振軍.UWB超寬帶無線通信技術研究[J].計算機工程與設計，2008,29(11):2748-2750.

[9]金亞秋，李中新.結合譜積分加速法的前后向迭代法數值計算分形粗糙介質面的雙站散射和透射[J].電子學報，2002,30(11):1648-1653.

[10]李杰.隨機粗糙面及其與目標復合電磁散射有限元與高頻方法建模研究[D].西安：西安電子科技大學，2012.

[11]朱小敏，任新成，郭立新.指數型分布粗糙地面電磁散射的FDTD研究[J].上海航天，2011,28(4):1-6.

[12]YEEKS.NumericalsolutionofinitialboundaryvalueproblemsinvolvingMaxwell’sequationinisotropicmedia[J].IEEETransactionsantennaspropagate, 1966，14(4)：302-307.

[13]葛德彪，閆玉波.電磁波時域有限差分方法[M].3版.西安：西安電子科技大學出版社，2011.

[14]WANGJR,SCHMUGGETJ.Anempiricalmodelforthecomplexdielectricpermittivityofsoilsasafunctionofwatercontent[J].IEEETransactionongeoscienceandremotesensing, 1980,18(4)：288-295.

[15]TSANGL，KONGJA，DINGKH,etal.Scatteringofelectromagneticwaves,Numericalsimulations[M].NewYork:JohnWileyandSons,2004.

[16]朱小敏，任新成. 隨機粗糙地面的寬帶電磁散射研究[J].河南科學，2014,32(8):1457-1461.

FDTDresearchofbroadbandbackwardelectromagneticscattering

fromexponentialdistributionroughlandsurface

WUJian,RENXin-cheng,ZHUXiao-min

(SchoolofPhysicsandElectronicsInformation,Yan'anUniversity,Yan'an716000,China)

Abstract∶We simulate exponential distribution rough land surface with Monte Carlo method.We also address wide-band electromagnetic scattering of rough land surface corresponding to Gaussian pulse incident wave by finite-difference time-domain (FDTD) method.Backward scattering coefficients of different frequency response are obtained through numerical calculation.We further analyze the influences of correlation length, root-mean-square of height fluctuation, soil moisture and incident angle variations on backward scattering coefficient.We eventually acquire wide-band backward electromagnetic scattering characteristics of exponential distribution rough land surface.

Key words∶electromagnetic scattering; FDTD; rough land surface; backward scattering coefficient; Gaussian pulse wave

中圖分類號：TN011

文獻標識碼：A

文章編號：1002-4026(2015)04-0083-06

作者簡介：武劍(1992-)，男，碩士研究生，研究方向為粗糙面電磁散射。 Email：yadxyjswj@163.com

基金項目：國家自然科學基金(61379026)；陜西省科學技術研究發展計劃(工業攻關)(2014K05-61)；陜西省教育廳科研計劃(14JK1830)

收稿日期：2014-11-22

DOI:10.3976/j.issn.1002-4026.2015.04.016