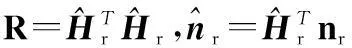基于二進制二次規劃全局最優性條件的GSSK系統的檢測算法
張新賀, 吳金隆, 門宏志, 金明錄
(1. 大連理工大學信息與通信工程學院, 遼寧 大連 116024;
2. 遼寧科技大學電子與信息工程學院, 遼寧 鞍山 114051)
?
基于二進制二次規劃全局最優性條件的GSSK系統的檢測算法
張新賀1,2, 吳金隆1, 門宏志1, 金明錄1
(1. 大連理工大學信息與通信工程學院, 遼寧 大連 116024;
2. 遼寧科技大學電子與信息工程學院, 遼寧 鞍山 114051)
摘要:廣義空間位移鍵控(generalized space shift keying, GSSK)技術作為大天線技術和綠色通信技術相融合的優選方案受到了業界的廣泛興趣,其特點是在每一時刻只激活幾根天線發送已知信號,利用激活天線的序號來傳遞信息。基于最大似然(maximum likelihood, ML)準則的GSSK檢測器,當天線數較多時,其計算量太大,給實際應用帶來困難,為此人們熱衷于研究簡化的次優檢測算法。給出了一種基于二進制二次規劃全局最優性條件的GSSK系統的檢測算法。該算法首先利用最優判決準則判斷發送信息,然后根據已判斷出的發送信息來確定發送天線的組合,進而得到發送的二進制比特流。仿真結果表明,所提出的新算法在性能上優于已有的正交匹配追蹤(orthogonal matching pursuit, OMP)、凸超集松弛(convex superset relaxation, CSR)等次優檢測算法,復雜度又低于ML算法,在性能和復雜度之間得到較好的折中。
關鍵詞:廣義空間位移鍵控; 二進制二次規劃; 全局最優性條件; 檢測算法
0引言
隨著移動用戶對通信需求的飛速增長,迫切需要更高的數據速率、更高的頻譜利用率和更低的實現復雜度的寬帶通信技術來滿足無線通信的需求。多天線多輸入多輸出(multiple input multiple output,MIMO)技術,可以實現更高頻譜利用率的寬帶無線通信。但是MIMO技術存在信道間干擾(inter-channel interference,ICI)、天線間同步(inter-antenna synchronization,IAS)和多射頻鏈路的問題,這就增加了接收端檢測和解調的難度。
空間調制(space modulation,SM)[1-5]是最近提出的一種新的MIMO傳輸技術,較好地克服了原MIMO技術的一些缺陷。其主要特點是在每一時刻只有一根天線被激活用于發送數據,將發送天線在天線陣列中的序號也作為一種新的“調制方式”來傳輸數據,這樣可以避免信道間干擾和天線間同步問題,因此降低了接收端解調的難度。但是在接收端最大似然(maximum likelihood, ML)最優檢測需要遍歷搜索被激活的天線序號和天線發送的符號,復雜度較高。空間位移鍵控(space shift keying, SSK)[6-7]是SM的一種簡化形式,它只利用天線序號來傳遞信息,而發送的信號是已知的信號。為了提高傳輸速率,在發送端可以激活多根天線,稱為廣義空間位移鍵控(generalized space shift keying, GSSK)[8-11]。因為在被激活的天線上發送相同的信號,在接收端只需檢測發送天線的序號,無需判斷天線發送的符號,復雜度較SM有所降低。另外,目前大天線技術和綠色通信技術受到業界的廣泛興趣,而GSSK技術作為這兩個技術融合的優選方案受到了業界的廣泛關注[2]。
與一般的MIMO系統一樣,廣義空間位移鍵控的最優解調也是基于ML準則的算法,但是其計算量會隨著天線數量的增加呈現指數型增長趨勢[12],給實際應用帶來困難,特別大天線情形下更是如此,因此人們熱衷于研究低復雜度的次優檢測算法。傳統的破零(zero forcing,ZF)、最小均方誤差(minimum mean square error,MMSE)等算法的計算復雜度很低,但是性能有限。最近,很多次優檢測算法被提出,以期獲得較好的檢測性能,如:正交匹配追蹤(orthogonal matching pursuit,OMP)算法[13]、凸超集松弛(convex superset relaxation,CSR)算法[14]、半定松弛(semidefinite relaxation,SDR)算法[14]等。但是上述算法在性能與ML算法仍存在一定差距。
與上述算法的思路不同,本文從另一個角度提出一種基于二進制二次規劃全局最優性條件的GSSK次優檢測算法,該算法在性能上均優于上述次優檢測算法,與ML性能基本相當。
本文余下內容安排如下:第1節介紹GSSK系統模型;第2節簡要介紹二進制二次規劃問題;在第3節給出基于二進制二次規劃的GSSK系統的檢測算法;第4節對仿真結果進行分析;最后在第5節給出本文的結論。
1系統模型
假設MIMO系統的發送天線數為NT,接收天線數為NR,每一時刻激活天線數為nt,GSSK系統模型如圖1所示。

圖1 GSSK系統模型

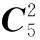

表1 GSSK映射表
因為GSSK系統也是一個MIMO系統,假設信道為平坦瑞利衰落信道,且信道增益在一個符號周期內保持不變,則接收信號可表示為
y=Hx+n
(1)
式中,y=[y1,y2,…,yNR]T為NR維接收信號矢量,x=[x1,x2,…,xNT]T為NT維發送信號矢量,由于每一時刻只激活nt根天線,因此x矢量中包括nt個“1”,NT-nt個“0”。H是NR×NT維的信道增益矩陣,每個元素hi,j為獨立同分布的零均值、單位方差的復高斯隨機變量;n=[n1,n2,…,nNR]T是均值為0,方差為σ2的加性復高斯白噪聲矢量。

下面考慮式(1)的ML檢測問題,其準則可以表示為
(2)
式中,M為發送信號矢量集合。
因為xi的取值只有1和0兩種可能,因此式(2)的優化問題可以轉化為二進制二次規劃問題。


即

(3)

將式(3)實數化處理,得
(4)
式中,Re(·),Im(·)分別表示取其實部和虛部。因此式(2)的最大似然檢測準則可表示為等價的二進制二次規劃問題:
(5)

2二進制二次規劃問題
由第1節知道,GSSK信號的ML檢測問題可看成二進制二次規劃問題。本節給出二進制二次規劃全局最優性條件和最優性判決準則。根據文獻[15],利用最優性判決準則可以在較小的計算開銷下,求得部分最優解。為此,先介紹二進制二次規劃全局最優條件。
2.1二進制二次規劃全局最優性條件
考慮如下一般二進制二次規劃優化問題:

(6)
式中,x=[x1,x2,…,xn]T;Q為n×n維的對稱矩陣;c∈Rn。
可以證明,x為問題(6)的全局最優解的最優性必要條件為[15-16]:
XQXe+Xc≤diag(Q)e
式中,X=diag(x)=diag(x1,x2,…,xn),e=[1,1, …,1]T,diag(Q)為n×n維的對角矩陣,對角線元素為qii。上式的分量形式為
(7)
式中,ei=[0,…,0,1,0,…,0]T,第i個元素為1,其他元素都為0。
2.2最優性判決條件
本節推導最優性判決準則。考慮如下的二進制二次規劃優化問題,即
(8)
它與式(6)的最優問題完全等價,因此直接利用式(6)的最優性條件,可以得到式(8)的最優性條件為
其分量形式為
(9)

(10)

(11)

因此,可得到如下判決準則[16]:
(12)
算法的具體實現,可以采用多次迭代的方法。不失一般性,考慮第1次迭代的情況,按先后順序逐一判斷第1根到第NT根發送天線的信息碼。若ri不滿足判決準則(12),則跳過第i根發送天線,繼續判斷第i+1根發送天線,直到遍歷所有NT根發送天線為止。此時可以得到部分最優解,然后將其作為已知條件對問題(8)進行迭代反饋。以上迭代過程循環進行,直到無法檢測出新的信息碼為止。
3基于二進制二次規劃的GSSK檢測算法

為了便于算法描述,令nd表示通過最優判決準則檢測出的+1的個數,nu表示通過最優判決準則沒有檢測出來的個數。
算法描述如下:
第2步:利用第1步求得的部分全局最優解來確定式(5)的解,即發送信號矢量,分以下3種情況進行討論。
情況 1利用最優性判決準則判決出NT根發送天線的信息。
(1) 若nd>nt,則將已經檢測出的|ri-Si|值最小的nd-nt個+1改判為-1。若該向量包含在M中,則判定為發送信號矢量;否則進行ML檢測確定發送信號矢量。
(2) 若nd=nt,如果該向量包含在M中,則判定為發送信號矢量;否則進行ML檢測確定發送信號矢量。
(3) 若nd 情況 2利用最優性判決準則判決出部分發送天線的信息。 (1) 若nd>nt,則將已經檢測出的|ri-Si|值最小的nd-nt個+1改判為-1,其他NT-nd個元素判為-1。若該向量包含在M中,則判定為發送信號矢量;否則進行ML檢測確定發送信號矢量。 (2) 若nd=nt,將沒有檢測出來的元素均判為-1。如果該向量包含在M中,則判定為發送信號矢量;否則進行ML檢測確定發送信號矢量。 (3) 若nd ①如果nu+nd≥nt,將已經判決出的+1、-1信息作為部分最優解,將集合M中包含此部分最優解的向量構成一個新的集合,然后在新集合中進行小規模ML檢測判斷發送信號矢量。 例:設式(5)的部分全局最優解為x=[+1,-1,*,*,*]T,其中*表示沒有判決出來。此時新的可能的發送矢量集合為{(+1,-1,+1,-1,-1), (+1,-1,-1,+1,-1), (+1,-1,-1,-1,+1)},在這一集合中進行小規模ML檢測判斷發送信號矢量。 ②如果nu+nd 情況 3利用最優性判決準則沒有判決出任何發送天線的信息。 此時采用ML檢測確定發送信號矢量。 第3步根據第2步求得的發送信號矢量,確定激活天線序號,反映射后得到發送二進制比特流。 由于本算法是基于二進制二次規劃(binaryquadraticprogramming,BQP)的檢測算法,因此下文將該算法稱為BQP算法。 4仿真結果及分析 為了驗證BQP算法的有效性,本節將該算法與ML算法、OMP算法、CSR算法進行了比較,并分析了算法的復雜度。 4.1仿真結果 為了從誤碼率角度更直觀地體現BQP算法的有效性,在NT=16,nt=4,NR=16(以下簡寫為16-16-4)和NT=16,nt=8,NR=16(以下簡寫為16-16-8)兩種情況下,將BQP算法與ML算法、OMP算法、CSR算法進行比較,仿真曲線如圖2所示。圖中,橫坐標為信噪比(signal-to-noise ratio, SNR),縱坐標為誤碼率(bit error rate, BER)。仿真時,每幀發送長度為100 000。 圖2 BQP算法與ML、OMP、CSR算法誤碼率性能的比較 從圖2給出的仿真曲線可看出,在相同SNR下,BQP算法比OMP算法和CSR算法的誤碼率低,與ML算法的性能基本相當。 4.2復雜度分析 以下給出幾種GSSK檢測算法的復雜度分析。 (1) ML檢測算法 (2)OMP檢測算法 根據文獻[13]中的NCS檢測算法和文獻[17]中的信號恢復的OMP算法,首先應該對信道增益矩陣H的每一列進行歸一化處理,然后采用OMP算法進行稀疏重構,算法的復雜度主要取決于文獻[17]中的步驟2,大約為O(NTNRnt)。 (3)CSR檢測算法 根據文獻[14]中的CSR檢測算法,即 (13) (4) 本文提出的BQP算法 圖3 BQP算法第2步實數乘法次數占ML算法的百分比 從圖3中可看出,在低信噪比時,算法第2步的實數乘法次數占ML算法的比例較低。隨著信噪比的增加,該比例會隨之增加,主要是由于滿足最優判決準則的二進制信息碼的概率隨信噪比的增加而降低(判決概率見定理)。當信噪比達到一定程度時,算法第2步的運算量維持在恒定值。從圖3中可看出,在信噪比為10 dB時,16-16-4、16-16-8兩種情況下算法第2步實數乘法次數占ML算法的比例分別為62%和51%。假設信道增益矩陣H在整個傳輸過程中保持不變,則無需計算R。因此BQP算法的運算量等于計算r的實數乘法次數加上算法第2步的實數乘法次數。在上述兩種情況下,BQP算法的實數乘法次數分別占ML算法的64%和51%。表2給出了信噪比為10dB時兩種情況下BQP算法和ML算法運算量的比較。 表2 BQP和ML算法復雜度的比較 表3給出了BQP算法與OMP算法、CSR算法、ML算法復雜度的比較。其中BQP算法的復雜度中的p為表2中給出的百分比。當p<1時,BQP算法的復雜度低于ML算法,高于CSR算法、OMP算法。當p>1時,BQP算法的復雜度高于ML算法。 表3 BQP與OMP、CSR、ML算法復雜度的比較 綜上所述,BQP算法的復雜度取決于最優判決和部分ML檢測。當最優判決完全失敗時,BQP算法做了無用功,后續的ML檢測規模沒有變小,總的運算量高于ML算法(多了計算r所需的實數乘法次數)。因此,BQP算法的有效性很大程度上依賴于最優判決的結果。如果判決結果越好,后續的ML檢測規模就越小,算法總的復雜度就越小。 下面分析這一檢測概率。 因為ri>Si和ri<-Si是互斥事件,所以滿足最優判決準則的概率可表示為 (14) 由式(4)得 (15) (16) 式中,ui=[Ri1,Ri2,…,RiNT]T∈RNT,下面給出GSSK系統最優判決準則的檢測概率。 定理 1對于GSSK系統的檢測問題,滿足判決準則的二進制變量的概率為 (17) 式中,Nc表示發送信號矢量集合M的大小。 證畢 式(17)給出了接收端對發送矢量每一元素的檢測概率。當系統的噪聲方差越大,即信噪比越小時,通過最優判決準則判決檢測的概率就越大,BQP算法第2步需要進行部分ML檢測需要的實數乘法次數就越低,此時BQP算法的復雜度低于ML算法。隨著系統信噪比的增加,通過最優判決準則判決檢測的概率降低,BQP算法第2步進行部分ML檢測需要的實數乘法次數就越多,此時BQP算法的復雜度會增加。當最優判決完全失敗時,BQP算法復雜度高于ML算法。 5結論 目前,大天線技術和綠色通信技術受到業界的廣泛興趣,而GSSK技術作為這兩個技術融合的優選方案,本文的算法不僅有較好的實際應用意義,而且也代表了另一種思路,對相關的信號檢測算法也有參考意義。 參考文獻: [1] Mesleh R Y, Haas H, Sinanovic S, et al. Spatial modulation[J].IEEETrans.onVehicularTechnology,2008,57(4):2228-2241. [2] Di Renzo M,Haas H,Ghrayeb A,et al.Spatial modulation for generalized MIMO:challenges,opportunities,and implementation[J].ProceedingsoftheIEEE,2014,102(1):56-103. [3] Rajashekar R, Hari K V S, Hanzo L. Reduced-complexity ML detection and capacity-optimized training for spatial modulation systems[J].IEEETrans.onCommunications, 2014, 62(1): 112-125. [4] Liu W L, Wang N, Jin M L, et al. Denoising detection for the generalized spatial modulation system using sparse property[J].IEEECommunicationsLetters, 2014, 18(1): 22-25. [5] Xiao Y, Yang Z F, Dan L L, et al. Low-complexity signal detection for generalized spatial modulation[J].IEEECommunicationsLetters, 2014, 18(3): 403-406. [6] Jeganathan J, Ghrayeb A, Szczecinski L, et al. Space shift keying modulation for MIMO channels[J].IEEETrans.onWirelessCommunications, 2009, 8(7): 3692-3703. [7] Zhou E, Hao L. Optimal power allocation for space shift keying modulation in a distributed antenna system[J].IEEECommunicationsLetters, 2013, 17(9):1734-1737. [8] Chang R Y, Lin S J, Chung W H. New space shift keying modulation with hamming code-aided constellation design[J].IEEEWirelessCommunicationsLetters, 2012, 1(1): 2-5. [9] Di Renzo M, Haas H. Improving the performance of space shift keying (SSK) modulation via opportunistic power allocation[J].IEEECommunicationsLetters, 2010, 14(6): 500-502. [10] Jeganathan J, Ghrayeb A, Szczecinski L. Generalized space shift keying modulation for MIMO channels[C]∥Proc.oftheIEEE19thInternationalSymposiumonPersonal,IndoorandMobileRadioCommunications,2008: 1-5. [11] Ntontin K, Di Renzo M, Perez-Neira A, et al. Adaptive generalized space shift keying[J].EURASIPJournalonWirelessCommunicationsandNetworking, 2013(1): 1-15. [12]Larsson E G. MIMO detection methods: how they work[J].IEEESignalProcessingMagazine, 2009, 26(3): 91-95. [13]Yu C M, Hsieh S H, Liang H W, et al. Compressed sensing detector design for space shift keying in MIMO systems[J].IEEECommunicationsLetters, 2012, 16(10): 1556-1559. [14]Chang R Y, Chung W H, Lin S J. Detection of space shift keying signaling in large MIMO systems[C]∥Proc.oftheWirelessCommunicationsandMobileComputingConference(IWCMC), 2012: 1185-1190. [15]Beck A, Teboulle M. Global optimality conditions for quadratic optimization problems with binary constraints[J].SIAMJournalonOptimization, 2000, 11(1): 179-188. [16]Liu W L, Pei Y Y, Jin M L. Partial optimal MIMO detection for BPSK communication system[J].JournalofSignalProcessing,2013,29(10):1315-1322.(劉文龍,裴瑩瑩, 金明錄. BPSK通信系統的部分最優MIMO檢測算法[J].信號處理, 2013, 29(10):1315-1322.) [17] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEETrans.onInformationTheory, 2007, 53(12): 4655-4666. [18] Shang Y, Fromherz M P J, Crawford L. A new constraint test-case generator and the importance of hybrid optimizers[J].EuropeanJournalofOperationalResearch, 2006, 173(2): 419-443. [19] Guo L M, Luo D Y. A TOA/AOA hybrid location method in nonline-of-sight environment[J].JournalofCircuitandSystems, 2010, 15(5): 26-30.(郭麗梅, 羅大庸. 非視距環境中TOA/AOA混合定位方法[J].電路與系統學報, 2010, 15(5): 26-30.) 張新賀(1980-),男,講師,博士研究生,主要研究方向為空間調制系統檢測、壓縮感知理論的應用及稀疏信號的重構。 E-mail:cdaszxh@sina.com 吳金隆(1989-),男,碩士研究生,主要研究方向為MIMO系統信號檢測、空間調制系統信號檢測。 E-mail: wujinlong@mail.dlut.edu.cn 門宏志(1988-),女,博士研究生,主要研究方向為空間調制系統檢測、壓縮感知理論的應用及稀疏信號的重構。 E-mail: menruiye@sina.com 金明錄(1958-),男,教授,博士研究生導師,博士,主要研究方向為信號與通信系統基礎理論和技術。 E-mail: mljin@dlut.edu.cn 網絡優先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150202.1727.004.html Detection algorithm for GSSK system based on global optimality conditions for binary quadratic programming ZHANG Xin-he1,2, WU Jin-long1, MEN Hong-zhi1, JIN Ming-lu1 (1.SchoolofInformationandCommunicationEngineering,DalianUniversityofTechnology, Dalian116024,China; 2.SchoolofElectronicandInformationEngineering, UniversityofScienceandTechnologyLiaoning,Anshan114051,China) Abstract:Generalized space shift keying (GSSK), a preferred scheme in the combination of the large-antenna technology and the green communication technology, has received a wide range of interests. The main features of GSSK are that only a few antennas are activated at any time instant and antenna indices are exploited to convey information. The computational complexity of the maximum likelihood (ML) detector is extremely high due to the large transmit-antenna which has been the limitation in practical application. Thus, simplified suboptimal detection algorithms have been widely studied. A novel GSSK detection algorithm based on global optimality conditions for binary quadratic programming is proposed. The proposed algorithm uses the optimal decision criterion to judge the transmit information. Subsequently the algorithm can determine the combination of transmit antennas based on the previous transmit information. Thus, the transmit binary bit stream is estimated. The simulation results show that the performance of the proposed algorithm, which exhibits lower computational complexity, is better than orthogonal matching pursuit (OMP) and convex superset relaxation (CSR) suboptimal detection algorithms. The proposed method achieves a better tradeoff between the performance and complexity. Keywords:generalized space shift keying (GSSK); binary quadratic programming; global optimality conditions; detection algorithm 作者簡介: 中圖分類號:TN 914 文獻標志碼:A DOI:10.3969/j.issn.1001-506X.2015.07.30 基金項目:國家自然科學基金(61301130)資助課題 收稿日期:2014-09-18;修回日期:2014-12-16;網絡優先出版日期:2015-02-02。