改進的基于三階段故障過程狀態檢測模型

王慧穎, 王文彬

(北京科技大學東凌經濟管理學院, 北京 100083)

?

改進的基于三階段故障過程狀態檢測模型

王慧穎, 王文彬

(北京科技大學東凌經濟管理學院, 北京 100083)

摘要：基于維修實踐中設備兩階段故障過程,利用延遲時間的概念和當前時刻的狀態檢測歷史信息,建立了改進的基于三階段故障過程的狀態檢測模型。該模型更接近于設備的真實運行過程。設備運行有4種可能狀態出現:正常狀態、非嚴重缺陷狀態、嚴重缺陷狀態和故障狀態。當檢測到系統處于非嚴重缺陷狀態時,采用延遲預防維修策略建立模型。以單位時間設備運行平均費用最小為決策目標,優化檢測間隔和閾值時間,通過參考閾值時間來決定是否實施延遲預防維修決策。最后將提出的模型應用于實際案例中,驗證了改進的基于三階段故障過程的狀態檢測模型的有效性。

關鍵詞：延長時間; 三階段故障過程; 狀態檢測; 維修策略

0引言

隨著科學技術的迅猛發展,檢測技術正日趨先進和完善,對設備進行檢測的自動化程度也越來越高,以故障前的缺陷為出發點來研究維修問題將變得日趨可行和切實有效。在設備維修中,對設備運行狀態進行檢測，其目的是發現設備運行中的故障隱患,也就是缺陷,從而實施正確的預防維修行為。1976年Christer教授提出延遲時間概念[1],此概念將系統故障過程分為兩個階段:正常運行階段和故障延遲階段。之后,Christer和Waller將其應用于生產線檢修問題中[2],通過對設備實施檢測鑒別設備的運行狀態。基于延遲時間概念的模型不僅適用于多部件設備也適用于單部件設備[1-8]。諸如文獻[9-17],利用延遲時間理論建立系統績效和檢測間隔期之間關系,從而獲得最佳檢測間隔期并證明該理論的有效性。在實際的維修工作中,維修人員根據系統所處的缺陷程度劃分出更多的狀態,如工業中的“紅黃綠”三色代表著系統的不同狀態。文獻[18]將兩階段的故障過程擴展為三階段故障過程,也即將故障延遲時間階段細分為非嚴重缺陷階段和嚴重缺陷階段,當系統被檢測到處于非嚴重缺陷階段時不采取任何預防維修行為,一旦檢測到處于嚴重缺陷狀態時再采取預防維修行為,然而延遲維修的時間長度是不確定的,這并不符合實際情況。文獻[19]中考慮到三階段故障過程的雙重點檢策略(大檢和小檢),這兩種檢測策略的范圍和程度不同,在檢測中一旦發現缺陷立即維修更新,然而此模型并沒有根據缺陷的不同程度來考慮是否需要延遲預防更新的情況。

本文考慮到單個設備在壽命周期內,檢測出缺陷的可能性是隨工齡而變化的,前期使用中一般不易發生異常狀態,因此在這段時間內對設備的維修管理工作還處于觀察和準備中,如購買所需備件等,那么一旦在這段時期內設備被檢測出處于缺陷階段時,可能會因為維修準備工作不足而導致需要延遲預防維修。如果在多個相同設備同時工作的情況下,預防維修時間需要事先安排,那么通常會在預防維修時間(如月修、年修)對所有的設備實施預防維修工作。如果在這個預防維修時間之前,檢測發現某個設備處于缺陷運行狀態時,會根據缺陷的程度考慮是否需要延遲預防維修，直到預先安排的預防維修時間再進行維修,利用設備在不嚴重缺陷狀態下工作仍然能夠完成預定的功能。本文采用延遲預防性維修策略,這種策略更符合實際維修情況,不僅減少對生產的影響,而且有利于減少維修次數,避免過度維修而造成的浪費,充分利用設備的有效使用壽命,同時也有利于備件管理[20],當備件發生緊急缺貨時可以參照延遲維修的時間長度來考慮普通訂購備件還是緊急訂購備件。在案例研究中,引入文獻[7]中給出的另一種預防維修策略,并與本文提出的預防維修策略進行比較。檢測間隔的決策也是維修管理中的關鍵,因為檢測間隔太小會無形中增加檢測的費用,檢測間隔太大又會增加因故障發生而產生的經濟損失。

1基于延遲時間的故障過程

在設備維修過程中,可以觀察到設備從開始使用到發生故障,這個過程可以分為兩個階段,如圖1所示。第1階段是從設備開始運行到缺陷發生時刻u,這個階段表示設備處于正常運行狀態;第2階段是從缺陷發生時刻u到故障發生時刻x,這個階段表示設備處于缺陷運行狀態(在沒有任何維修行為發生的情況下),該階段也被稱為故障延遲階段,延遲時間用h表示[21]。當設備處于第1階段時,對設備運行狀態進行檢測,檢測信號比較平穩;當設備處于第2階段時,檢測信號出現異常,并呈現出異常的變化趨勢,這階段就應該是維修人員關注的重點[22]。缺陷狀態出現后可導致兩種維修形式[23]:一種是故障維修,就是由于缺陷出現最終導致故障,從而需要停工進行修理。另一種是預防維修,在檢測中發現缺陷并停工進行維修(如更換磨損的零部件)。在故障延遲階段,可以考慮更細致的劃分,將缺陷分為嚴重缺陷和非嚴重缺陷[18]。本文在建立模型時會考慮到缺陷的嚴重程度,從而采取相應的維修決策。

圖1　兩階段延遲時間模型

2問題描述和建模假設

2.1問題描述

考慮單零部件設備系統(如小水泵、交通燈和電池等)遭到單個故障的延遲時間模型如圖2所示。白圓點表示零部件在某時刻出現的缺陷(由1,2,3表示),黑原點表示零部件在某時刻由缺陷導致的故障(由10,20,30表示),A,B為檢測時刻。在A時刻進行一次檢測(屬于完美檢測[7],即零部件出現的缺陷能夠完全被檢測出來),那么缺陷1能被檢測出來,這里會考慮一個決策變量閾值時DT,在DT之前如果缺陷1非嚴重,考慮延遲預防維修直到DT時刻在進行預防維修,如果缺陷1很嚴重則考慮立即進行預防維修。在DT之后發現缺陷,無論缺陷達到什么程度都需要立即進行預防維修,避免故障10的發生,狀態被更新。如果檢測是在B時刻發生,那么缺陷2已經發生了故障20,需要立即進行故障維修,達到狀態更新。另外,AB之間的檢測間隔也是需要考慮的變量。通過上述的3種狀態更新策略建立改進的基于三階段故障過程的狀態檢測模型,以單位時間設備運行平均維修費用最小為決策目標,確定最佳檢測間隔和閾值時間。

圖2　單部件設備遭到單個故障的延遲時間模型

2.2建模假設

(1) 本文所研究的設備為單部件設備遭到單個故障的情況;

(2) 設備一旦發生故障可立即被識別出;對設備實施完美檢測,每隔T單位時間進行一次檢測,記錄設備的運行狀態;

(3) 考慮到缺陷的嚴重程度,將故障過程分為3個階段:正常運行階段(U),非嚴重缺陷運行階段(X)和嚴重缺陷運行階段(Y);設備有4種狀態:正常狀態、非嚴重缺陷狀態、嚴重缺陷狀態和故障狀態;

(4) 如果在閾值時間DT之前發現設備處于非嚴重缺陷狀態,則延遲預防維修行為直到DT時刻在執行;

(5) 如果在閾值時間DT或之后發現缺陷,無論缺陷達到什么程度將立即對系統進行預防維修,使系統完全恢復其功能;檢測過程也將重新開始。

其他相關符號的含義如下:

U表示正常運行階段,U的概率密度函數為g(u);

X表示非嚴重缺陷運行階段,X的概率密度函數和累積分布函數分布為f1(x)和F1(x);

Y表示嚴重缺陷運行階段,Y的概率密度函數和累積分布函數分布為f2(y)和F2(y);

T為檢測間隔;

Tf為故障發生的時刻;

Tp為檢測時發現非嚴重缺陷狀態的時刻;

Tq為檢測時發現嚴重缺陷狀態的時刻;

D為第D次檢測,相應的時刻為DT時刻也即閾值時間;

Cs為檢測平均費用;

Cp為檢測更新平均費用;

Cf為故障更新平均費用;

E(C,T,D)為更為更新周期內的期望費用,T和D為決為決策變量;

E(L,T,D)為更新周期的期望長度,T和D為決策變量。

3模型建立

設備從開始工作到被更新(發生故障或檢測出缺陷),這個時間段稱為一個更新周期。為了計算更新周期內的期望費用和更新周期的期望長度,考慮第k個檢測周期,即[(k-1)T,kT]。

3.1故障更新的概率

在一個檢測間隔內故障更新發生的概率,存在兩種情況:

(1) 設備在[(k-1)T,kT]中發生故障,但在kT之前的(k-1)次檢測點并沒有發現設備的不正常狀態,因此設備的故障延遲階段和發生故障時刻Tf,Tf∈[(k-1)T,kT]發生在同一個檢測間隔內,如圖3所示。

圖3　第1種故障事件

因此,在任意檢測區間[(k-1)T,kT]內,設備因發生故障而進行故障更新的概率為

(1)

式中,k=1,2,…。

從設備運行到發生故障，整個工作時間為Tf∈((k-1)T+z,(k-1)T+z+dz),則期望更新周期費用E(C1)和期望更新周期長度E(L1)分別為

(2)

(3)

(2) 設備在閾值時間DT之前的第k次檢測,初次識別出設備處于非嚴重缺陷運行狀態,采用延遲維修策略,但設備提前在第k+i個區間[(k+(i-1))T,(k+i)T]內發生故障,如圖4所示。

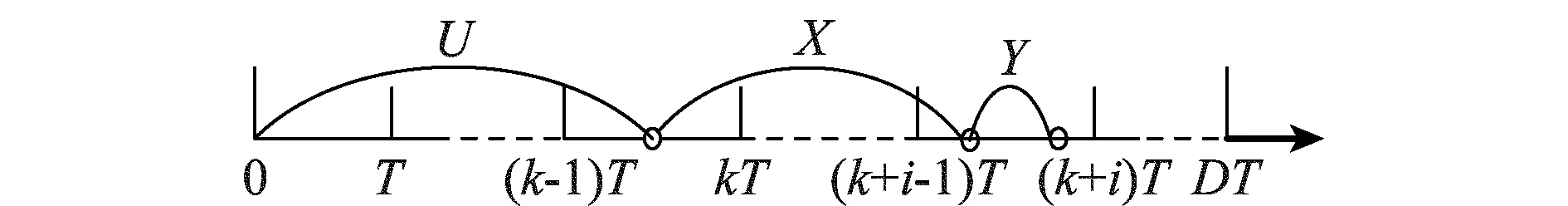
圖4　第2種故障事件

因此,在任意檢測區間[(k+(i-1))T,(k+i)T]內,設備因發生故障而進行故障更新的概率為

(4)

式中,i=1,2,…,D-k;k=1,2,…,D-1。

從設備開始運行到發生故障，整個工作時間為Tf∈((k+(i-1))T+z,(k+(i-1))T+z+dz),則期望更新周期費用E(C2)和期望更新周期長度E(L2)分別為

(5)

(6)

3.2檢測更新的概率

在DT之前, 第k-1次檢測點未發現缺陷狀態,但在區間[(k-1)T,kT]中出現缺陷,在kT時刻初次識別出設備處于非嚴重缺陷運行狀態,采用延遲預防維修策略。因檢測更新的概率有兩種,如圖5所示。

圖5　在DT之前發現缺陷事件

(1) 存在非嚴重缺陷的設備在延遲到DT時刻進行更新之前未發展成嚴重缺陷或故障,如圖5(a) 所示。

因此,設備運行到DT時刻而進行的預防更新的概率為

(7)

式中,k=1,2,…,D。

期望更新周期費用E(C3)和期望更新周期長度E(L3)分別為

(8)

(9)

(2) 如圖5(b) 所示,存在非嚴重缺陷的設備延遲到DT時刻進行預防更新,但在區間[(k+(i-1))T,(k+i)T]內已經發展成為嚴重缺陷,因而在(k+i)T時刻進行預防更新的概率為

(10)

式中，i=0,1,…,D-k;k=1,2,…,D。

期望更新周期費用E(C4)和期望更新周期長度E(L4)分別為

(11)

(12)

在DT之后的第k個檢測點測出設備處于缺陷狀態(非嚴重或嚴重),都在(D+k)T時刻立即進行預防更新,如圖6所示,其概率公式分別為

(13)

(14)

式中,k=1,2,…。

圖6　在DT之后發現缺陷事件

期望更新周期費E(C5)和期望更新周期長度E(L5)分別為

(15)

(16)

3.3費用模型

根據文獻[7,18]的更新費用理論,考慮所有的檢測區間和所有的可能情況，將式(2)、式(3)、式(5)、式(6)、式(8)、式(9)、式(11)、式(12)、式(15)和式(16)代入式(17),求得模型的單位時間設備運行平均費用C(T,D)為

(17)

以單位時間設備運行平均費用最小為決策目標,確定最佳檢測間隔T和閾值D。

4案例分析

以英國教學醫院醫學物理系的醫療設備為研究對象,每個醫療設備的維修信息被記錄在維修卡片上,信息包括購買醫療設備日期、醫療設備預防維修日期、故障發生日期及醫療設備工作的相關描述。本文研究輸液泵和蠕動泵的預防維修策略,它們主要應用于重癥病人護理、神經外科及心臟病人護理。因此為了保證輸液泵和蠕動泵的正常工作,制定合理的預防維修策略從而減少醫療設備因停機而無法及時救治病人的情況,這是醫療部門最關心的問題。

為了應用本文所建立的模型,確定出合理的預防維修間隔期。因此,收集了輸液泵和蠕動泵的故障維修和預防維修數據記錄,輸液泵一共有105個,它的主要故障模式來源于壓力傳感器故障;蠕動泵一共有35個,它的主要故障模式來源于電池故障。這兩個醫療泵在缺陷運行狀態下仍能完成預定功能,缺陷狀態需定期檢測來識別出,故障狀態能夠立即被識別出。它們的相關維修數據和工作原理的詳細描述,見文獻[24]。采用威布爾分布描述醫療泵的退化過程的三階段:正常運行階段U、非嚴重缺陷運行階段X和嚴重缺陷運行階段Y。使用最大似然方法來估計參數值,應用文獻[18]中所提出的似然函數進行參數估計,因此所獲得的參數估計值如表1所示。在維修卡片中,不包括任何維修費用的信息,但平均檢測費用和檢測平均更新費用的估計值是比較容易給出的,醫院維修工作人員能夠提供相應的信息。然而故障更新費用的估計值很難給出,因為醫療泵一旦發生故障,所帶來的經濟損失遠遠高于醫療泵本身的價值。相關維修費用(以天為單位)如表2所示。采用枚舉法求解等式(17),在Matlab軟件環境下,通過編程實現。

表1　醫療泵故障三階段的威布爾分布參數

表2　相關維修費用估計　元

為了證明本文提出模型的有效性,將文獻[7]中提出的預防維修策略在三階段延遲時間模型的基礎上建模,定義為模型2,并與本文提出的模型(定義為模型1)進行比較。模型2的維修策略不考慮缺陷的程度,一旦識別出醫療泵處于缺陷狀態,立即對醫療泵進行預防維修。

模型2的故障更新概率:在第(k-1)次檢測時未發現缺陷運行狀態,但醫療泵在區間[(k-1)T,kT]內發生故障,因故障更新的概率公式和式(1)一樣。期望更新周期費用E(C1)和期望更新周期長度E(L1)與式(2)和式(3)一樣。

模型2的檢測更新概率:設備在前(k-1)次檢測都處于正常運行狀態,但在kT檢測測出設備處于缺陷狀態(非嚴重或嚴重),都立即進行狀態更新。概率公式分別為

(18)

P(Tq=kT)=

(19)

期望更新周期長度E(L2)和期望更新周期費用E(C2)分別為

(20)

(21)

將式(2)、式(3)、式(20)和式(21)代入式(17),采用枚舉法求解等式(17),確定最佳檢測間隔T。

4.1案例計算及結果分析

圖7　選擇參數設置1的情況下,模型1中單位時間蠕動泵工作平均費用的優化過程　　　　　　　　圖8　選擇參數設置2的情況下,模型1中單位時間輸液泵工作平均費用的優化過程

選擇參數設置1(蠕動泵)TD*C1(T,D)TD*E(T,D)選擇參數設置2(輸液泵)TD*C1(T,D)TD*E(T,D)4101.325115*13*1.0972*114.10231223.25906111.228118121.1021223.75931423.28458121.169420121.1127433.45171623.326110121.132922111.1282633.31931823.381612131.110324111.1473833.26432013.440714131.099226101.168510*3*3.2513*2213.5095

圖9　選擇參數設置1的情況下,模型1(D*=13)和　　　模型2的比較　　　　　　圖10　選擇參數設置2的情況下,模型1(D*=3)和　　　模型2的比較

4.2檢測成本的閾值

圖11和圖12 分別給出了檢測成本在一定范圍內變化時,模型1和模型2的單位時間設備運行最小平均費用的變化情況。由圖可以看出,在優化蠕動泵的預防維修計劃中檢測成本小于275時和在優化輸液泵的預防維修計劃中檢測成本小于400時,模型1的最優期望費用要小于模型2的最優期望費用,當檢測成本分別大于275和大于400時,模型2的策略更優。由此,可以確定檢測蠕動泵和輸液泵的檢測成本閾值分別為275和400。此外,對于不同的檢測成本,圖11和圖12也給出了基于延遲預防維修策略的最優檢測間隔期T和閾值D,也證明了當檢測成本不超過檢測成本閾值時,對蠕動泵和輸液泵采用延遲預防維修策略是最優的。例如,圖11中(13,15,1.09)表示當檢測成本Cs=50時,最優檢測間隔期T=15,最優閾值D=13和單位時間設備運行最小平均費用為1.09。

圖11　不同檢測成本下,優化蠕動泵的預防維修計劃

圖12　不同檢測成本下,優化輸液泵的預防維修計劃

5結束語

本文建立了改進的基于三階段故障過程的狀態檢測模型,以單位時間設備運行平均費用為決策目標,優化設備系統的預防維修的檢測間隔和閾值時間。為設備檢測間隔決策提供了定量化的方法,提出了設備故障更新概率和檢測更新概率的計算方法,最后將模型1與模型2通過應用于實際案例進行比較和分析,證明了模型1是有效的。

參考文獻：

[1] Christer A H, Wang W. Delay-time-based maintenance model of a multicomponent system[J].IMAJournalofManagementMathematics,1995, 6(2):205-222.

[2] Christer A H, Waller W M. Reducing production downtime using delay time analysis[J].JournaloftheOperationalResearchSociety, 1984, 35(6):499-512.

[3] Radouane L, Chateauneuf A, Djamil A. Opportunistic policy for optimal preventive maintenance of a multi-component system in continuous operating units[J].ComputersandChemicalEngineering, 2009,9(33): 1499-1510.

[4] Wang W, Christer A H. Solution algorithms for a nonhomogeneous multicomponent system inspection model[J].ComputerandOperationsResearch,2003,30(1),19-34.

[5] kumura S O, Jardine A K S, Yamashina H. Inspection policy for a deteriorating single-unit system characterized by a delay-time model[J].InternationalJournalofProductionResearch, 1996,9(34):2441-2460.

[6] Jia X S,Christer A H,Smith M A J. The modeling study for functional check of mechanical wear process[J].ChinaMechanicalEngineering,1998,9(12): 34-37.(賈希勝,克萊斯特,史密斯.針對機械磨損過程的功能檢測模型[J].中國機械工程, 1998,9(12): 34-37.)

[7] Wang W.Delaytimemodelling[M].In D.N.P. Murthy and AKS. Kobbacy (Eds),Complexsystemmaintenancehandbook. London: Springer, 2008:345-370.

[8] Wang W. An inspection model for a process with two types of inspections and repairs[J].ReliabilityEngineeringandSystemSafety, 2009, 94(2):526-533.

[9] Cerone P. On a simplified delay time model of reliability of equipment subject to inspection monitoring[J].JournaloftheOperationalResearchSociety,1991,42(6): 505-511.

[10] Wang W. A model of multiple nested inspections at different intervals[J].ComputersandOperationsResearch, 2000, 27(6):539-558.

[11] Wang W, Banjevic D, Pecht M. A multi-component and multi-failure mode inspection model based on the delay time concept[J].ReliabilityEngineeringandSystemSafety,2010,95(8):912-920.

[12] Wang W, Banjevic D. Ergodicity of forward times of the renewal process in a block-based inspection model using the delay time concept[J].ReliabilityEngineeringandSystemSafety, 2012, 100: 1-7.

[13] Das A N, Acharys D. Age replacement of components during IFR delay time[J].IEEETrans.onReliability,2004,53(3): 306-312.

[14] Zhao J, Chan A H, Roberts C, et al. Reliability evaluation and optimization of imperfect inspections for a component with multi-defects[J].ReliabilityEngineeringandSystemSafety,2007,92(1):65-73.

[15] Leung F, Kit-leung M. Using delay-time analysis to study the maintenance problem of gearboxes[J].InternationalJournalofOperationsandProductionManagement,1996,16(12):98-105.

[16] Pillay A, Wang J, Wall A D, et al. A maintenance study of fishing vessel equipment using delay-time analysis[J].JournalofQualityinMaintenanceEngineering,2001,7(2):118-128.

[17] Jones B, Jenkinson I, Wang J. Methodology of using delay-time analysis for a manufacturing industry[J].ReliabilityEngineeringandSystemSafety,2009,94(1): 111-124.

[18] Wang W. An inspection model based on a three-stage failure process[J].ReliabilityEngineeringandSystemSafety,2011,96(7): 838-848.

[19] Wang W B, Zhao F, Peng R. Modeling of the optimal multiple inspection policy based on a three-stage failure process[J].SystemEngineeringTheory&Practice,2013,34(1): 223-232.(王文彬,趙斐,彭銳.基于三階段故障過程的多重點檢策略優化模型[J].系統工程理論與實踐,2013,34(1):223-232.)

[20] Wang W, Syntetos A A. Spare parts demand: linking forecastiong to equipment maintenance[J].TransportationResearchPartE,2011,6(47):1194-1209.

[21] Wang W. An overview of the recent advances in delay-time-based maintenance modeling[J].ReliabilityEngineeringandSystemSafety,2012,(106):165-178.

[22] Wang Y, Wang W B, Fang S F, et al. A two-stage prediction model research on condition-based maintenance[J].JournalofHarbinEngineeringUniversity,2007,28(11):1278-1281.(王英,王文彬,方淑芬,等.狀態維修兩階段預知模型研究[J].哈爾濱工程大學學報,2007,28(11): 1278-1281.)

[23] Sun W. The delay-time model and its application in the equipment maintenance[J].JournalofArmoredForceEngineeringInstitute, 1995,9(3): 85-91.(孫偉.延遲時間模型及其在設備維修中的應用[J].裝甲兵工程學院學報,1995,9(3): 85-91.)

[24] Baker R D, Wang W. Estimating the delay time distribution of faults in repairable machinery from failure data[J].IMAJournalofManagementMathematics,1991,3(4): 259-281.

王慧穎(1981-),女,博士研究生,主要研究方向為復雜系統故障預測。

E-mail:wanghuiying120454@163.com

王文彬(1956-),男,教授,博士,主要研究方向為復雜系統故障預測。

E-mail:wangwb@ustb.edu.cn

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150317.0953.003.html

Improved inspection model based on a three-stage failure process

WANG Hui-ying, WANG Wen-bin

(DonglingSchoolofEconomicsandManagement,UniversityofScienceand

Technology,Beijing100083,China)

Abstract:Aiming at the typical two-stage failure process of equipment in maintenance practice, an inspection model based on a two-stage failure process is designed based on the obtained condition monitoring information using the concept of delaying time. This model is a step closer to reality. There are four operation states: normal state, minor defective state, severe defective state and failure state. If the system is identified to be in the minor defective stage, two different kinds of maintenance decisions are made .The optimal intervals and threshold valve time for inspection of potential failure are determined with the minimum cost using this model. The threshold value time plays a role to decide whether to carry out the preventive maintenance action. Finally, the proposed model is applied to a practical case and the results prove the effectiveness of the model based on the delay preventive maintenance policy.

Keywords:delay time; three-stage failure process; state inspection; maintenance decision

作者簡介：

中圖分類號：TP 18

文獻標志碼：A

DOI:10.3969/j.issn.1001-506X.2015.07.37

基金項目：國家自然科學基金重點項目 (71231001)；中國博士后科學基金 (2013M530531); 中央高校基本科研業務費專項資金 (FRF-MP-13-009A, FRF-TP-13-026A); 教育部博士導師基金(20120006110025)資助課題

收稿日期：2014-08-21；修回日期：2014-12-20；網絡優先出版日期：2015-03-17。