錐 b-度量空間中擴張映象的強式耦合疊合點的存在性
宋艷霞, 柴國慶, 袁喆
(湖北師范學院 數學與統計學院,湖北 黃石 435002)
錐 b-度量空間中擴張映象的強式耦合疊合點的存在性
宋艷霞, 柴國慶, 袁喆
(湖北師范學院 數學與統計學院,湖北 黃石435002)
摘要:在錐 b-度量空間中, 作者引進了強式耦合疊合點的定義, 提出了一個新的擴張映象條件, 并證明了在此擴張映象條件下強式耦合疊合點的存在性.
關鍵詞:錐 b-度量空間;擴張映象;強式耦合疊合點
中圖分類號:O177.91
文獻標識碼:A
文章編號:1009-2714(2015)04- 0073- 06
doi:10.3969/j.issn.1009-2714.2015.04.015
收稿日期:2015—10—09
作者簡介:宋艷霞(1989—),女,湖北襄陽人,碩士研究生,主要研究方向為非線性泛函分析.
0引言
關于擴張映象不動點定理的研究, 1967年最先開始于Machuca[1].以后Jungck[2], Fisher[3],王尚志[4]等先后討論了一些其它形式的擴張映象的不動點定理.2011年, 作為對b-度量空間和錐度量空間的推廣, Hussain and Shah[9]提出了錐b- 度量空間的概念. 在此空間中, 他們建立了一些局部的拓撲性質, 并把度量空間的一些壓縮映象推廣到了錐b- 度量空間,并證明了不動點的存在性, 此外,他們也在這個空間中探究了兩個映象及多個映象的公共不動點問題.
本文需要用到的如下預備知識.
設E 是一個實Banach空間,θ表示Ε 中的零元素,Ε的子集Ρ 稱為一個錐, 若滿足:
1) Ρ是非空閉集合, 即Ρ≠{θ} ;
2)a,b是非負實數, 若x,y∈P, 則ax+by∈P;
3)x∈P 且 -x∈P, 則有x=θ.
對于任意的錐P?E, 在P上定義了一個偏序“≤” , 滿足若x≤y當且僅當y-x∈P, 而“< ”表示x≤y且x≠y.用 int P表示 P的內部, 若x?y表示y-x∈int P. 如果存在一個實數K滿足當y≥x≥θ時, 有‖x‖≤K‖y‖,則稱P 是正規的, 滿足這個條件的最小正數K稱為P 的正規常數.
在本文中總假設 P是正規體錐.
定義1[2]設X 是一個非空集合,E 是一個實Banach空間, P 是一個錐并在E 定義了一個偏序“≤”,d:X×X→E稱為 X中帶有常數s≥1的一個錐b- 度量空間, 若滿足下面的條件:
a)d(x,y)≥θ,對于任意的x,y∈X.d(x,y)=θ當且僅當x=y;
b)d(x,y)=d(y,x), 對于任意的x,y∈X;
c)d(x,z)≤s[d(x,y)+d(y,z)] , 對于任意的x,y,z∈X .
定義2[2]設(X,d) 是一個錐b- 度量空間,{xn} 是X 中的一個序列, 并且x∈X ,
1)對于任意的c∈E 當c?θ時, 如果存在一個正整數N0當n≥N0時, 有d(xn,x)?c, 則稱xn為收斂的, 并且x是{xn} 的極限, 記為xn→x.

2)對于任意的c∈E 當c?θ時, 如果存在一個正整數N0,當n,m≥N0時, 有d(xn,xm)?c,則稱{xn} 為X 中的一個柯西列.
3)如果X 中的每個柯西列{xn} 都是收斂的, 則稱錐b- 度量空間(X,d) 是完備的.
引理1[2]1) 如果E 是一個實Banach空間, P 是一個錐, 當元素a∈P 且對0<λ<1 時有a≤λa,則a=θ.
2) 如果c∈int P,an≥θ當n→∞時有an→θ,則存在正整數N, 當n≥N時, 有an?c.
3) 如果a≤b且b?c, 則a?c.
4) 若對于任意的c?θ, 有θ≤μ≤c則μ=θ.
定義3[2]一對元素(x,y)∈X2如果它同時滿足gx=F(x,y),gy=F(y,x) 則稱它為映象F:X2→X和g:X→X的耦合疊合點; 如果滿足x=gx=F(x,y),y=gy=F(y,x) 則稱它為映象F:X2→ X和g:X→X 的耦合不動點.
定義4 一對元素(x,x)∈X2稱為映象F:X2→X 和g:X→X 的強式耦合疊合點, 如果它滿足
gx=F(x,x)
顯然, 強式耦合疊合點一定是耦合疊合點, 它得到的結論比定義4得到的結論更好. 特別地, 當g=I(恒等映象)時有x=F(x,x) ,則稱為映象的強式耦合不動點.
定義5映象F:X2→X 和g:X→X, 若對任意的x∈X,有g(X)?F(x,X) 記為g(X)?F(·,X);若對任意的x∈X 有g(X)?F(X,x), 記為g(X)?F(X,·)
在錐b- 度量空間中, 人們比較多討論關于壓縮映象的不動點, 而討論擴張映象相對較少. 本文章引進了強式耦合疊合點的定義, 提出了一類新的關于兩個映象的擴張映象, 并證明了強式耦合疊合點的存在性.
1 主要結論
本文建立了如下強式耦合疊合點定理.
定理1設(X,d) 是一個錐b- 度量空間,s≥1,P是一個體錐,F:X2→X 和g:X→X 是兩個映象, 并且存在ai≥0,i=1,2,3,4,5 使得
a2+(a1+a5)s-a4s(1+s)>s,a2>a4s,a2>sa3+s
成立, 滿足下面的擴張條件
d(F(x,y),F(u,v))≥a1d(gy,F(x,y))+a2d(gv,F(u,v))-a3d(gy,F(u,v))-
a4d(gv,F(x,y))+a5d(gx,gu)
(1)
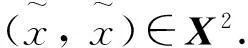
證對于任意的x0∈X, 由于g(X)?F(·,X) 則存在x1∈X 使得gx0=F(x0,x1) .存在x2∈X, 使得gx1=F(x1,x2)繼續下去,就可以得到存在xn∈X, 使得gxn-1=F(xn-1,xn),n=1,2,……, 從而
d(gxn-1,gxn)=d(F(xn-1,xn),F(xn,xn+1))≥
a1d(gxn,F(xn-1,xn))+a2d(gxn+1,F(xn,xn+1))-a3d(gxn,F(xn,xn+1))-
a4d(gxn+1,F(xn-1,xn))+a5d(gxn-1,gxn)=
a1d(gxn,gxn-1)+a2d(gxn+1,gxn)-a3d(gxn,gxn)-
a4d(gxn+1,gxn-1)+a5d(gxn-1,gxn)=
(a1+a5)d(gxn-1,gxn)+a2d(gxn,gxn+1)-a4d(gxn-1,gxn+1)
(2)
由于
d(gxn-1,gxn+1)≤s[d(gxn-1,gxn)+d(gxn,gxn+1)]
(3)
故
d(gxn-1,gxn+1)≥(a1+a5)d(gxn-1,gxn)+a2d(gxn,gxn+1)-
a4s[d(gxn-1,gxn)+d(gxn,gxn+1)]=
(a1+a5-sa4)d(gxn-1,gxn)+(a2-sa4)d(gxn,gxn+1)
整理可得
(sa4+1-a1-a5)d(gxn-1,gxn)≥(a2-sa4)d(gxn,gxn+1)
由條件a2>sa4, 有
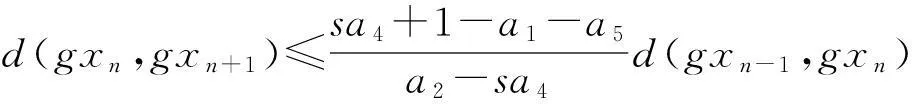
(4)
i)若sa4+1-a1-a5≤0, 由(4)式知d(gxn,gxn+1)=θ. 由于n的任意性, 可知gxn=gxn-1=gxn-2=…=gx1=gx0. 由
d(gx1,F(x0,x0))=d(gx0,F(x0,x0))=
d(F(x0,x1),F(x0,x0))≥
a1d(gx1,F(x0,x1))+a2d(gx0,F(x0,x0))-a3d(gx1,F(x0,x0))-
a4d(gx0,F(x0,x1))+a5d(gx0,gx1)=
a1d(gx1,gx0)+a2d(gx0,F(x0,gx0)-sa3d(gx1,gx0)-
sa3d(gx0,F(x0,x0))-a4d(gx0,gx0)+a5(gx0,gx0)
由于
d(gx1,F(x0,x0))≤s[d(gx1,gx0)+d(gx0,F(x0,x0))]
從而
sd(gx0,F(x0,x0))≥a2d(gx0,F(x0,x0))-sa3d(gx0,F(x0,x0))
(5)
可得到
(a2-sa3-s)d(gx0,F(x0,x0))≤θ
由a2-sa3-s>0 知d(gx0,F(x0,x0))=θ.故gx0=F(x0,x0) ,從而(x0,x0) 為映象F和g的強式耦合疊合點.
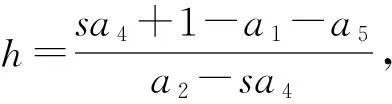
d(gxn,gxn+1)≤hd(gxn-1,gxn),n=1,2 …
故
d(gxn+1,gxn)≤hd(gxn,gxn-1)≤h2d(gxn-1,gxn-2)≤…≤hnd(gx1,gx0)
當m>n≥1時
d(gxn,gxm)≤sd(gxn,gxn+1)+s2d(gxn+1,gxn+2)+…+sm-nd(gxm-1,gxm)≤
shnd(gx1,gx0)+s2hn+1d(gx1,gx0)+…+sm-nhm-1d(gx1,gx0)≤
shn(1+sh+…+(sh)m-n-1d(gx1,gx0)≤
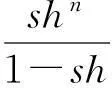
(6)
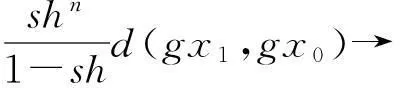
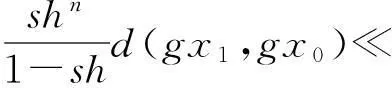
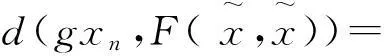
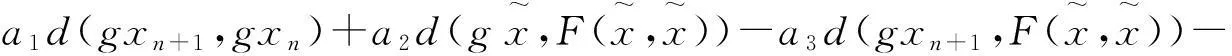
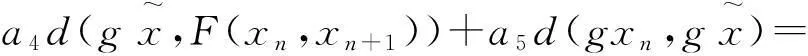
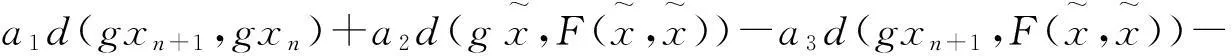
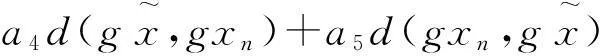
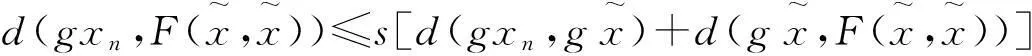
(7)
整理(7)式可得
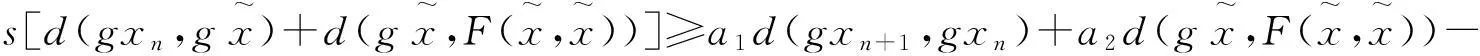
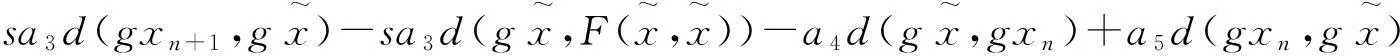
在上式中, 令n→∞, 可得
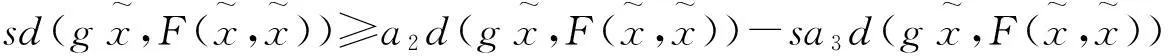
(8)
注1當定理1中的g=I (恒等映象)時, 會得到推論1, 如下.
推論1設(X,d) 是一個完備的錐b- 度量空間,s≥1,P是一個體錐,F:X2→X為一一映象, 若存在ai≥0,i=1,2,3,4,5 使得
a2+(a1+a5)s-a4s(1+s)>s,a2>a4s,a2>sa3+s
成立, 若X?F(·,X) 滿足下面的擴張條件
d(F(x,y),F(u,v))≥a1d(y,F(x,y))+a2d(v,F(u,v)-a3d(y,F(u,v))-
a4d(v,F(x,y))+a5d(x,u)
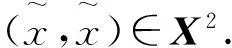
定理2設(X,d) 是錐b- 度量空間,s≥1,P是體錐,F:X2→X 和g:X→X 是兩個映象, 并且存在ai≥0,i=1,2,3,4,5,使得
sa1+a2-a4s(1+s)>s,a2+a5>a4s,a2>sa3+s,+a5a4s,a2sa3+s
成立, 滿足下面的擴張條件
d(F(x,y),F(u,v))≥a1d(gx,F(x,y))+a2d(gu,F(u,v))-a3d(gx,F(u,v))-
a4d(gu,F(x,y))+a5d(gx,gu)
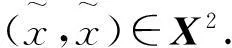
證類似于定理1的證明, 簡略如下.
對于任意的x0∈X,由于g(X)?F(X,·) 則存x1∈X,使得gx0=F(x1,x0) . 存在x2∈X,使得gx1=F(x2,x1) …繼續下去,就可以得到存在xn∈X, 使得gxn-1=F(xn,xn-1),n=1,2, …,從而
d(gxn-1,gxn)=d(F(xn,xn-1),F(xn+1,xn))≥
a1d(gxn,F(xn,xn-1))+a2d(gxn+1,F(xn+1,xn))-a3d(gxn,F(xn+1,xn))-
a4d(gxn+1,F(xn,xn-1))+a5d(gxn,gxn+1)
(9)
類似于(2)(3)的證明,(9)式可得
d(gxn-1,gxn)≥(a2+a5)d(gxn,gxn+1)+a1d(gxn-1,gxn)-
a4s[d(gxn-1,gxn)+d(gxn,gxn+1)]=
(a2+a5-sa4)d(gxn,gxn+1)+(a1-sa4)d(gxn-1,gxn)
整理得
(sa4+1-a1)d(gxn-1,gxn)≥(a2+a5-sa4)d(gxn,gxn+1)
由條件a2+a5>a4s, 從而
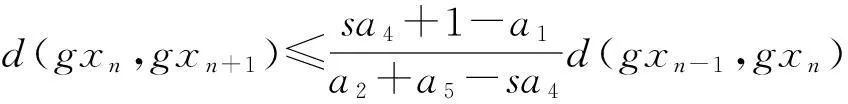
(10)
i)若sa4+1-a1≤0, 由(10)式知d(gxn-1,gxn)=θ, 由n的任意性, 可知gxn=gxn-1=gxn-2=…=gx1=gx0由
d(gx1,F(x0,x0))=d(gx0,F(x0,x0))=
d(F(x1,x0),F(x0,x0))≥
a1d(gx1,F(x1,x0))+a2d(gx0,F(x0,x0))-a3d(gx1,F(x0,x0))-
a4d(gx0,F(x1,x0))+a5d(gx1,gx0)=
a1d(gx1,gx0)+a2d(gx0,F(x0,x0))-sa3d(gx1,gx0)-
sa3d(gx0,F(x0,x0))-a4d(gx0,gx1)+a5d(gx1,gx0)
類似于(5)的證明, 整理可得
(a2-sa3-s)d(gx0,F(x0,x0))≤θ
同理, 由a2-sa3-s>0知d(gx0,F(x0,x0))=θ.故gx0=F(x0,x0) ,從而(x0,x0) 為映象F和g的強式耦合疊合點.
ii) 若sa4+1-a1>0,
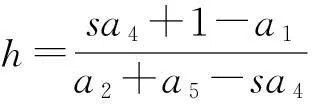
d(gxn,gxn+1)≤hd(gxn-1,gxn),n=1,2,…
故
d(gxn+1,gxn)≤hd(gxn,gxn-1)≤h2d(gxn-1,gxn-2)≤…≤hnd(gx1,gx0)

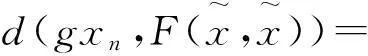
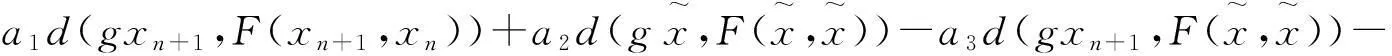
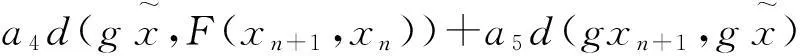
(11)
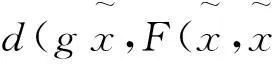
注2當定理2中的 g=I(恒等映象)時, 會得到推論2, 如下.
推論2設(X,d) 是一個完備的錐b- 度量空間,s≥1,P是一個體錐,F:X2→X 為一一映象, 若存在ai≥0,i=1,2,3,4,5 使得
sa1+a2-a4s(1+s)+a5>s,a2+a5>a4s,a2>sa3+s
成立, 如果X?F(X,·) 滿足下面的擴張條件 X?F(X,·)
d(F(x,y),F(u,v))≥a1d(x,F(x,y))+a2d(u,F(u,v))-a3(x,F(u,v))-
a4d(u,F(x,y))+a5d(x,u)
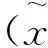
參考文獻:
[1]R.A Machua coincidence theorem [J].Amer Math Monthly, 1967,74:569.
[2]Jungck G.Commuting maps and fixed points[J]. Am Math Mon,1976,83: 261~263.
[3]Fisher B, Mappings with a common fixed point J Math[J].Seminar Notes,1979,7:81~83.
[4]王尚志, 李伯渝, 高志明.膨脹算子及其不動點定理[J]. 數學進展,1982,11(2):149~153.
[5]Fadail Z M,Ahmad A G B.Coupled coincidence point and common coupled fixed point results in cone b-metric spaces[J].Fixed point Theory Appl,(2013) 2013:177.
[6]Betilik-Pilarska A.The fixed point property for some generalized nonexpansive mappings and renormings[J]. Fixed point Theory Appl,(2015)2015:800-813.
[7]Shatanawi W,Awawdeh F.Some fixed and coincidence point theorms for expansive maps in cone metric spaces[J] .Fixed point Theory Appl,(2012)2012:19.
[8]Mehmeed N.Multivalued fixed point results in cone metric spaces[J].Fixed point Theory Appl,(2015)2015:156~170.
[9]Hussain N, Shah M H.KKM mappings in cone b -metric spaces[J]. Comput Math Appl,2011,62(4):1677~1684.
[10]Cho S H, Bae J S. Fixed point theorems for multi-valued maps in cone metric spaces[J].Fixed Point Theory Appl. (2011),81~89.
[11]Agarwal R P, Kadelburg Z, Radenovi'c S. On coupled fixed point results in asymmetric G-metric spaces[J].J. Inequal. Appl.2013 (2013) 528~671.
[12]Golubovi'c Z,Kadelburg Z,Radenovi'c S.Coupled coincidence points of mappings in ordered partial metric spaces[J].
AbstractAppl Anal,2012:14~89. In this paper, author introduce a definition of strong coupled coincidence point, present a new expansive map, and prove the existence of the strong form of coupled coincidence point under this condition in cone b-metric spaces
[13]Kadelburg Z,Radenovi'c S.Coupled fixed point results under tvs-cone metric and w-cone-distance[J].Adv Fixed Point Theory,2012,2:29~46.
[14]Fitting M. Fixed point semantics for logic programming: a survey[J]. Theoret Comput,2002, 278:1~2 .
[15]Przymusinski T C. Every logic program has a natural stratification and an iterated least fixed point model, in: Proceedings of the Eighth ACM Sympo-sium on Principles of Database Systems[J].PODS,( 1989):11~21.
[16]Cho S H, Bae J S.Fixed point theorems for multi-valued maps in cone metric spaces[J].Fixed Point Theory Appl. (2011)2011:71.
Existence on the strong form of coupled coincidence point
for expansive maps in cone b-metric spaces
SONG Yan-xia, CHAI Guo-qing, YUAN Zhe
(College of Mathematics and Statistics, Hubei Normal University, Huangshi435002,China)
Key words:cone b-metric spaces; expansive maps; strong form of coupled coincidence point

