四參數Logistic模型潛在特質參數的Warm加權極大似然估計*

孟祥斌 陶 劍, 陳莎莉

(1東北師范大學教育學部; 2東北師范大學數學與統計學院, 應用統計教育部重點實驗室;3中國基礎教育質量監測協同創新中心東北師范大學分中心, 長春 130024)

1 引言

近30年來, 隨著統計和計算機技術的飛速發展, 項目反應理論(Item Response Theory, IRT)的研究和應用取得了長足的進步。時至今日, 它已取代經典測量理論成為測量學研究的核心內容, 并在考試測評的諸多領域發揮著重要的作用。

在IRT中, 單維二值評分模型的理論和技術最為成熟, 應用也最為廣泛。二值記分模型通常假設被試的潛在特質參數與反應的正確概率之間滿足Logistic函數或者Probit函數關系。這兩類模型在一定程度上是等價的, 但Logistic模型因其參數估計容易計算而廣受青睞, 成為IRT領域最為重要的一族模型。根據項目參數個數的不同, 常用的Logistic模型分為單參數、兩參數和三參數(1PL, 2PL和3PL)模型。模型包含的參數越多, 模型所描述的現象就越廣泛, 但參數估計對算法的要求也會越高。近年來, 隨著IRT理論體系的日趨完善, 測量學者們開始努力嘗試四參數Logistic (4-Parameter Logistic, 4PL)模型的理論與應用研究。

四參數模型的構想最早是由Barton和Lord在1981年提出的, 目的是為了考慮高能力被試作答失誤的可能, 他們建議在3PL模型的基礎上加入一個小于1的項目特征曲線上漸近線參數。最初該參數被限定為公共參數, 與項目無關。隨后一些研究發現(Linacre, 2004; Rupp, 2003; Tavares, de Andrade,& Pereira, 2004; Waller &Reise, 2009)不同項目特征曲線的上漸近線是存在差異的, 上漸近線參數被定義為項目參數更加科學。于是, 4PL模型的表達式為,

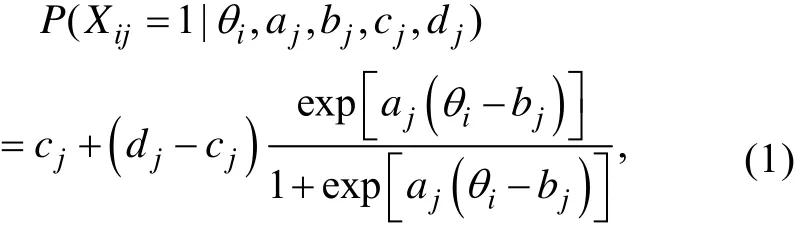
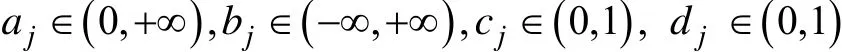
長期以來, 4PL模型的發展速度都非常緩慢,一直沒有引起測量學界的廣泛關注。主要原因是4PL模型的參數估計沒有被很好解決, 難以滿足測試的實際需要, 進而導致4PL模型的實際價值也沒有得到充分驗證。近些年, 關于4PL模型的理論與應用研究相繼取得一些突破性的研究成果, 例如,Linacre (2004)和Rupp (2003)對上漸近線參數的價值進行了深入的討論, 并給出了參數估計的計算方法。Loken和Rulison (2010)給出了4PL模型參數貝葉斯估計的Markov chain Monte Carlo (MCMC)算法, 有效解決了4PL模型項目參數的標定, 這對4PL模型的使用具有重要意義。Rulison和Loken (2009)驗證了, 在計算機自適應測試(computerized adaptive testing, 簡稱CAT)中, 使用4PL模型能夠提高被試潛在特質參數估計的精度。隨后, Green(2011), Liao,Ho, Yen和Cheng (2012)、Yen, Ho, Liao, Chen和Kuo(2012)相繼從多方面對4PL模型在CAT環境中的應用進行了更為深入的研究, 所得結果均表明4PL模型要優于傳統的3PL模型。Magis(2013)對4PL模型信息函數的性質進行了系統研究, 并給出一種信息函數最大值點的求解方法。此外, 在其它領域,4PL模型也有諸多成功地實踐, 如有興趣可查看以下文獻(Osgood, McMorris, &Potenza, 2002; Waller&Reise,2009; Tavares et al., 2004)。綜上所述, 無論是從方法論的角度, 還是基于實用性的目的, 4PL模型均具有極大的潛力和較高的應用價值。可以預見, 隨著4PL模型理論體系的日趨完善, 它必將成為未來主流的IRT模型之一, 在心理和教育測量的諸多領域發揮著不可替代的作用。

潛在特質參數的估計是IRT的主要內容之一,常用的方法有以下3種：(1)極大似然估計(maximum likelihoodestimate, MLE); (2)后驗期望估計(expected a posteriori estimate, EAPE); (3)最大后驗概率估計(maximum a posterioriestimate, MAPE)。在實際應用中, MLE和EAPE是最常用的兩種估計方法, 它們具備優良的大樣本性質。但是, 如果測試項目較少,將導致MLE和EAPE的效能降低, 難以保證估計的無偏性和準確性。潛在特質參數估計的無偏性對項目反應模型的應用非常重要, 如果參數估計的偏差較大, 將給進一步更為深入的測評帶來嚴重誤差(Warm, 1989;Penfield& Bergeron, 2005; Magis, 2014)。針對MLE和EAPE的這一不足, Warm在1989年提出一種3PL模型潛在特質參數的加權極大似然法,降低了估計的偏差。隨后, Wang和Wang (2001)以及Penfield和Bergeron (2005)分別在CAT和線性測試環境下, 把Warm的加權極大似然估計(weighted maximum likelihoodestimator, WMLE)推廣到廣義局部評分模型(generalized partial credit model, GPCM),并驗證了WMLE的優越性。

借鑒已有研究經驗, 本文以4PL模型為研究對象, 對其潛在特質參數的WMLE進行研究。首先,根據4PL模型的結構特點, 給出加權函數的構造公式。然后, 對加權極大似然方程的求解過程進行推導。最后, 通過計算機模擬在不同測試條件下對4PL模型潛在參數的WMLE、MLE和EAPE的性質進行比較, 以驗證WMLE的優越性。希望通過本文的研究, 能夠為4PL模型的應用提供科學而有效的參數估計技術。

2 方法

這部分首先對4PL模型潛在特質參數的MLE進行簡要介紹; 然后, 引出4PL模型潛在特質參數的WMLE并對相關計算過程進行詳細推導; 最后, 簡要給出4PL模型下潛在特質參數EAPE的計算公式。

2.1 極大似然估計(MLE)

對方程(2)兩端取自然對數得到對數似然函數,

因為該方程為非線性方程, 通常使用Newton-Raphson(N-R)迭代算法對其進行求解。

2.2 加權極大似然估計(WMLE)

令

l

表示加權似然函數, 根據加權似然的定義有

對方程(12)兩端取自然對數得對數加權似然函數為,

為了糾正估計的偏差, 根據Warm在1989年提出的加權理論,

f

(

θ

)必須且只需滿足以下等式條件,

不難發現, 根據方程(15)推導出

f

(

θ

)是非常困難的, 而且滿足條件的

f

(

θ

)也不唯一, 但這并不會阻礙WMLE的求解。由方程(14)可知, 只要能夠推導出

B

′(

θ

),加權似然方程(14)隨之確定, 整個過程

f

(

θ

)是不必知道的。因此, 本研究首先要解決的問題是對4PL模型下的

B

′進行推導, 然后再給出求解加權似然方程的N-R迭代算法。

可以證明, 對于4PL模型有以下等式成立,

詳細證明過程請參見附錄。

根據方程(1)、(8)和(9)可得方程(16)的具體形式為，

再根據信息函數

I

(

θ

)的定義有,

最后, 將方程(17)和(18)代入方程(15),

對方程(19)和方程(4)進行求和, 即可得到4PL模型的Warm加權似然方程(14)，由于該方程過于繁瑣, 這里就不給出它的具體形式了。

本研究采用N-R算法對4PL模型能力參數的Warm加權似然方程進行求解。根據定義, 4PL模型下方程(14)的N-R迭代公式如下,

其中,

2.3 后驗期望估計(EAPE)

EAPE與MLE相比, 優勢是對于極端的反應數據表現比較穩定且容易計算, 不足是EAPE的偏差較大, 容易受到錯誤先驗信息的影響。一般來說,當測試的項目數較少時, 建議使用EAPE, 在項目數較多時, MLE更受青睞。

在IRT中,

θ

的先驗分布通常選取為標準正態分布, 其密度函數記為

φ

(

θ

).根據定義, 標準正態先驗下的EAPE的計算公式如下,

表示

θ

的后驗概率密度函數。

將方程(27)代入方程(26), 整理得

3 模擬研究

為了探明WMLE的具體表現, 本次模擬通過設定不同的考試條件, 對WMLE、MLE和EAPE的偏度(bias)和返真性能進行比較研究, 并對相關影響因素進行分析。

3.1 模擬設計

不失一般性, 在這次模擬中,

θ

的真值取定為從?3.0到3.0以0.5為步長的間隔點, 共計13個不同的能力值。測驗長度

n

和項目區分度參數

a

是

θ

估計的主要影響因素, 為了考查它們的影響,

n

取定3個水平, 15, 30和50,

a

也取定3個水平, 0.5, 1.0和2.0, 交叉組合共生成9種測試條件. 每種測試條件下, 除

a

以外, 其它項目參數真值的選取方式如下:

按照以上設計選取參數真值后, 以4PL模型為真實模型, 為每個

θ

值隨機抽取測試反應向量1000組。然后, 計算每組反應數據對應的WMLE(

θ

)、MLE(

θ

)和EAPE(

θ

). 需要強調的是, 如果隨機抽取了全是0或全是1的反應向量, 應予以刪除, 進行重新抽取。這樣做的目的是為了使似然方程有解,即MLE(

θ

)存在。

最后, 為了比較3種估計方法的偏差和返真性能, 需要計算以下3種指標：平均偏差(mean error, ME)、絕對平均偏差(absolutemean error, ABME)和均方根誤差(rootmean squared error, RMSE ),

3.2 模擬結果

3.2.1 WMLE、MLE和EAPE的偏差比較

圖1和圖2展示了9種測驗條件下WMLE ()

θ

,MLE()

θ

和EAPE()

θ

的ME和ABME隨

θ

的變化曲線。經仔細觀察, 可以發現以下現象：(1)如圖1所示, WMLE()

θ

和EAPE(

θ

)的ME具有相同的變化趨勢, 當

θ

小于0.0(測試中心)時,它們的ME趨于正的, 即估計值比真值偏大; 當

θ

大于0.0時, 它們的ME趨于負的, 即估計值比真值偏小。MLE()

θ

的ME表現出恰恰相反的變化趨勢,0.0左側的

θ

值對應的ME趨于負的, 0.0右側的

θ

值對應的ME趨于正的。3種估計ME的變化趨勢與已有研究相吻合(Warm, 1989; Penfield & Bergeron,2005), 符合它們偏差的變化特點。(2)如圖2所示, 每種測試條件下, WMLE()

θ

的ABME都是3種估計中最小的, 其次是MLE(

θ

),EAPE()

θ

的ABME最大。這說明WMLE()

θ

的偏差最小(無偏性最佳), MLE()

θ

的偏差其次(無偏性居中), EAPE()

θ

的偏差最大(無偏性最差)。

(4)隨著

m

或

a

的增加, 3種估計的ABME均表現出減小的趨勢, 并且它們的差異也隨之減小。例如, 當

a

=2.0,

m

=50時, 3種估計的ABME均是9種測試條件下最小的, 并且3種估計ABME的差異也是最小的。此外,

m

和

a

對MLE(

θ

)和EAPE (

θ

)的ABME影響非常顯著, 而對WMLE(

θ

)的ABME影響微乎其微。甚至在

m

和

a

均較小的情況下, 例如, 當

a

=0.5,

m

=15時, WMLE(

θ

)也沒有表現出較大的偏差。這說明, 相比于其它兩種估計方法,WMLE的無偏性受實際情況影響較小, 保持了很高的穩定性。

3.2.2 WMLE、MLE和EAPE的返真性能比較

圖3展示的是, 9種測試條件下, 3種估計的RMSE隨

θ

的變化曲線. 經仔細觀察, 可以發現：

(2)WMLE(

θ

)的RMSE隨

θ

的變化比較穩定,即使對于極大或極小的

θ

值, 它的RMSE也沒有出現很大幅度的增加, 當

m

較大時, 它的RMSE曲線要更加平穩。這說明對于大多數

θ

值, WMLE(

θ

)都表現出優良的返真性能, 這對4PL模型的實際應用非常有意義。EAPE(

θ

)的RMSE隨

θ

的變化也較為穩定, 只是在

m

=15的條件下, 它的RMSE變化較為顯著。相比之下, MLE()

θ

的RMSE隨

θ

的變化最為劇烈, 隨著

θ

遠離0.0, MLE()

θ

的RMSE明顯增大, 返真性能明顯降低。

圖1 九種測試條件下, WMLE、MLE和EAPE的ME變化曲線

圖2 九種測試條件下, WMLE、MLE和EAPE的ABME變化曲線

圖3 九種測試條件下, WMLE、MLE和EAPE的RMSE變化曲線

(3)隨著

m

的增大, WMLE()

θ

、MLE()

θ

和EAPE()

θ

的RMSE均表現出顯著減小的趨勢, 而且它們之間的差異也隨之減小。隨著

a

的增加,EAPE()

θ

和WMLE()

θ

的RMSE表現為減小的趨勢,但MLE()

θ

的RMSE的變化跟

θ

的取值范圍有關。當

θ

在測試中心附近時, MLE()

θ

的RMSE隨的增加而減小, 否則, 隨

a

的增加而增大。線性測試的特點、

a

對測試信息量的影響以及MLE的大樣本性質,是導致這一現象的原因。根據MLE的大樣本性質可知, MLE()

θ

的精度完全由測試的信息量決定,在線性測試中,

a

越大, 距離測試中心較近的

θ

值的測試信息量越大, 而距離測試中心較遠的

θ

值的測試信息量越小。所以, 隨著

a

的不同, MLE()

θ

的RMSE表現出上述變化趨勢是符合MLE的性質的。(4)與偏差的表現類似, 隨著測試情況的變化,WMLE()

θ

的返真性能表現出較高的穩定性, 受測試條件的影響很小, 另外兩種估計方法的返真性能的穩定性相對較差, 易受考試實際情況影響。從實際應用的角度看, 方法性質的穩定性很重要, 性質穩定的方法意味著更加安全, 所以應更受青睞。

4 結論與展望

本文基于Warm的加權極大似然估計理論提出了適用于4PL模型潛在特質參數的WMLE。理論上, WMLE能夠保持較高的精度并降低潛在特質參數估計的偏差, 這對IRT模型的應用具有重要的意義。模擬研究的結果表明：與MLE和EAPE相比,WMLE表現出更加優良的統計性質。首先, WMLE的偏差要明顯小于MLE和EAPE; 其次, WMLE具有良好的返真性能, 保證估計具有較高的精度; 最后, WMLE的性質(偏差和返真性能)對測試長度和項目區分度的變化表現出良好的穩定性, 即使在測試長度較短或項目區分度較低的情況下, WMLE的性質依然良好。相比之下, MLE和EAPE的穩定性就要差一些, 測試長度對MLE有很大的決定作用,而項目區分度對EAPE的影響比較顯著。因此, 當測試的項目不多時, 不宜選用MLE, 當測試項目的區分度不高時, 需謹慎考慮選用EAPE。

在形式上, WMLE與MAPE完全一樣, 但WMLE并不要求權函數

f

(

θ

)是概率密度函數, 所以WMLE與MAPE在理論上存在本質的不同。近年來, Magis等一批學者對WMLE與MAPE的關系進行了深入研究, 取得了一些重要結果。Warm (1989)證明了2PL模型的WMLE與Jeffreys先驗下的MAPE (簡稱JMAPE)存在等價關系, 這一結論具有較高的學術價值, 也引起了人們的關注。Magis (2015)證明：在GPCM下這種等價關系依然成立。不過, Magis和Raiche (2012)的研究表明, 3PL模型的WMLE與JMAPE的等價關系不成立, 同水平

θ

的WMLE值要比JMAPE值稍大一些。3PL模型的WMLE是否與其它先驗下的MAPE存在等價關系, Magis的研究并未提及。4PL模型潛在特質參數的WMLE與MAPE是何關系, 能否與某種先驗下的MAPE等價,是值得我們進一步深入研究的問題。因為該問題比較復雜, 僅僅通過模擬比較難以得到一般性的結論,所以本文沒有對WMLE與MAPE的性質進行比較。

此外, 本次模擬研究是在線性測試的環境下進行的, 所得結論不能簡單的推廣到CAT。根據CAT的設計原理, 每個被試所作答的試卷都是為其“量身定做”的, 保證了測試中心與被試潛在特質水平的距離最小。由圖3可知, 當被試的潛在特質水平與測試中心非常接近時, EAPE表現出最好的返真性能。可見, 在CAT的環境下, 4PL模型的WMLE未必能具有與本研究類似的優良性, 很有可能EAPE具有最佳效果。但這僅僅是一種預想, 具體情況有待被進一步深入研究。

Baker, F. B., & Kim, S. H. (2004).

Item response theory:Parameter estimation techniques

. New York: Marcel Dekker.Barton, M. A., & Lord, F. M. (1981). An upper asymptote for the three-parameter logistic item response model. In

Research Bulletin

(pp. 81–20)

.

Princeton, NJ: Educational Testing Service.Green, B. F. (2011). A comment on early student blunders on computer-based adaptive tests.

Applied Psychological Measurement, 35

, 165–174.Liao, W. W., Ho, R. G., Yen, Y. C., & Cheng, H. C. (2012). The four-parameter logistic item response theory model as a robust method of estimating ability despite aberrant responses.

Social Behavior and Personality, 40

, 1679–1694.Linacre, J. M. (2004). Discrimination, guessing and carelessness asymptotes: Estimating IRT parameters with Rasch.

Rasch Measurement Transactions, 18

, 959–960.Loken, E., & Rulison, K. L. (2010). Estimation of a fourparameter item response theory model.

British Journal of Mathematical and Statistical Psychology, 63

, 509–525.Magis, D. A. (2013). Note on the item information function of the four-parameter logistic model.

Applied Psychological Measurement, 37

, 304–315.Magis, D. A. (2014). Accuracy of asymptotic standard errors of the maximum and weighted likelihood estimators of proficiency levels with short tests.

Applied Psychological Measurement, 38

, 105–121.Magis, D. A. (2015). A note on weighted likelihood and Jeffreys modal estimation of proficiency levels in polytomous item response models.

Psychometrika, 80

, 200–204.Magis, D. A., & Raiche, G. (2012). On the relationships between Jeffreys modal and weighted likelihood estimation of ability under logistic IRT models.

Psychometrika, 77

, 163–169.Mathilda, D. T. (2003).

IRT from SSI: BILOG-MG, MULTILOG,PARSCALE, TESTFACT

. Chicago, IL: Scientific Software International.Osgood, D. W., McMorris, B. J., & Potenza, M. T. (2002).Analyzing multiple-item measures of crime and deviance I:Item response theory scaling.

Journal of Quantitative Criminology, 18

, 267–296.Penfield, R. D., & Bergeron, J. M. (2005). Applying a weighted maximum likelihood latent trait estimator to the generalized partial credit model.

Applied Psychological Measurement, 29

, 218–233.Qi, S. Q., Dai, H. Q., & Ding, S. L. (2002).

Principles of modern educational and psychological measurement

. Beijing: Higher Education Press.[漆書青, 戴海琦, 丁樹良. (2002).

現代教育和心理測量學原理

. 北京: 高等教育出版社.]Rulison, K. L., & Loken, E. (2009). I’ve fallen and I can’t get up: Can high ability students recover from early mistakes in computerized adaptive testing?.

Applied Psychological Measurement, 33

, 83–101.Rupp, A. A. (2003). Item response modeling with BILOG-MG and MULTILOG for Windows.

International Journal of Testing, 3

, 365–384.Tavares, H. R., de Andrade, D. F., & Pereira, C. A. (2004).Detection of determinant genes and diagnostic via item response theory.

Genetics and Molecular Biology, 27

, 679–685.Waller, N. G., & Reise, S. P. (2009). Measuring psychopathology with non-standard IRT models: Fitting the four parameter model to the MMPI. In S. Embretson& J. S. Roberts (Eds.),

New directions in psychological measurement with modelbased approaches

(pp. 147–173). Washington, DC: American Psychological Association.Wang, S. D., & Wang, T. Y. (2001). Precision of Warm’s weighted likelihood estimates for a polytomous model in computerized adaptive testing.

Applied Psychological Measurement, 25

, 317–331.Warm, T. A. (1989). Weighted likelihood estimation of ability in item response theory.

Psychometrika, 54

, 427–450.Yen, Y. C., Ho, R. G., Liao, W. W., Chen, L. J., & Kuo, C. C.(2012). An empirical evaluation of the slip correction in the four parameter logistic models with computerized adaptive testing.

Applied Psychological Measurement, 36

, 75–87.

附錄

定理

：對于4PL模型(1), 有以下等式成立,

證明

：根據方程(6)和(7)有,