彎曲導(dǎo)波模態(tài)分離與頻散補(bǔ)償研究

陳 樂(lè)，王悅民，耿海泉，葉 偉，鄧文力

（海軍工程大學(xué)動(dòng)力工程學(xué)院，湖北 武漢 430033）

彎曲導(dǎo)波模態(tài)分離與頻散補(bǔ)償研究

陳 樂(lè)，王悅民，耿海泉，葉 偉，鄧文力

（海軍工程大學(xué)動(dòng)力工程學(xué)院，湖北 武漢 430033）

為減少超聲導(dǎo)波多模態(tài)和頻散特性對(duì)管道缺陷檢測(cè)應(yīng)用時(shí)的不利影響，研究彎曲導(dǎo)波模態(tài)分離和導(dǎo)波頻散補(bǔ)償?shù)姆椒āＪ紫葘?dǎo)波信號(hào)進(jìn)行時(shí)頻分析，并與理論計(jì)算的時(shí)頻曲線進(jìn)行對(duì)比，確定信號(hào)中的各個(gè)模態(tài)，然后將各個(gè)模態(tài)信號(hào)進(jìn)行頻散補(bǔ)償處理，最后將頻散補(bǔ)償后的信號(hào)相加，得到最后的結(jié)果。管道缺陷檢測(cè)實(shí)驗(yàn)表明，由多模態(tài)和頻散特性產(chǎn)生的多個(gè)波包可由STFT方法識(shí)別出每個(gè)波包所屬的模態(tài)，經(jīng)頻散補(bǔ)償后多個(gè)波包可對(duì)應(yīng)在同一缺陷位置。實(shí)驗(yàn)證明導(dǎo)波信號(hào)經(jīng)模態(tài)識(shí)別、分離和頻散補(bǔ)償后更利于缺陷的識(shí)別和定位，同時(shí)該方法也為彎曲導(dǎo)波的應(yīng)用提供理論基礎(chǔ)。

超聲導(dǎo)波；時(shí)頻分析；模態(tài)分離；頻散補(bǔ)償；缺陷定位

0 引 言

聲導(dǎo)波檢測(cè)是一種快速的無(wú)損檢測(cè)技術(shù)，其一大優(yōu)勢(shì)是在局部激發(fā)導(dǎo)波，即可對(duì)長(zhǎng)距離范圍內(nèi)管道進(jìn)行檢測(cè)，包括埋地或帶有包覆層的不可見(jiàn)區(qū)域[1-2]。超聲導(dǎo)波沿管道傳播時(shí)會(huì)在缺陷處發(fā)生反射，當(dāng)反射的導(dǎo)波信號(hào)被檢測(cè)到時(shí)，達(dá)到缺陷識(shí)別和定位的目的。導(dǎo)波信號(hào)中包含檢測(cè)區(qū)域內(nèi)管道結(jié)構(gòu)的所有信息[3]，對(duì)信號(hào)進(jìn)行恰當(dāng)?shù)奶幚恚梢缘玫奖粶y(cè)管道的健康信息。

導(dǎo)波具有多模態(tài)和頻散的特性，管道導(dǎo)波檢測(cè)時(shí)，非對(duì)稱加載將激勵(lì)出一系列彎曲模態(tài)的導(dǎo)波[4-5]，多模態(tài)導(dǎo)波信號(hào)會(huì)以模態(tài)簇的形式傳播，對(duì)管道缺陷的檢測(cè)產(chǎn)生不利影響，制約彎曲導(dǎo)波的實(shí)際應(yīng)用。對(duì)導(dǎo)波各個(gè)模態(tài)的識(shí)別、分離和頻散補(bǔ)償具有重要意義，國(guó)內(nèi)外學(xué)者對(duì)此開(kāi)展了相關(guān)研究。他得安等[6]利用二維傅里葉變換和Wigner-Ville分布對(duì)平板Lamb波進(jìn)行了分析，并指出該方法的優(yōu)缺點(diǎn)。周正干等[7]利用短時(shí)傅里葉變換方法，得出了鋁板內(nèi)導(dǎo)波信號(hào)中各頻率成分隨時(shí)間的變化情況，分析出導(dǎo)波信號(hào)的模式轉(zhuǎn)換現(xiàn)象。關(guān)于頻散補(bǔ)償放的研究，Wilcox等[8]利用逆傅里葉變換的方法將頻散的時(shí)間-幅值信號(hào)變?yōu)榉穷l散的距離-幅值信號(hào)，消除了頻散效應(yīng)的影響。Fink等[9-10]利用陣列傳感器和時(shí)間反轉(zhuǎn)的方法實(shí)現(xiàn)了導(dǎo)波信號(hào)在缺陷處的聚焦，避免了頻散效應(yīng)的影響。Zeng等[11]通過(guò)設(shè)計(jì)激勵(lì)波形實(shí)現(xiàn)導(dǎo)波在特定距離處的頻散補(bǔ)償；Liu等[12]提出一種線性映射技術(shù)，將波數(shù)按照線性泰勒展開(kāi)法展開(kāi)，用于頻散特性的消除。

以上研究都是針對(duì)平板Lamb波展開(kāi)的，且大多是針對(duì)單一模態(tài)導(dǎo)波的補(bǔ)償，本文針對(duì)管道彎曲模態(tài)導(dǎo)波的頻散特性，利用時(shí)頻分析和頻散補(bǔ)償方法進(jìn)行分析，實(shí)現(xiàn)彎曲模態(tài)導(dǎo)波的識(shí)別、分離和頻散補(bǔ)償，有利于彎曲模態(tài)導(dǎo)波在工程上的應(yīng)用。

1 彎曲導(dǎo)波時(shí)頻分析和頻散補(bǔ)償原理

1.1 彎曲導(dǎo)波的激發(fā)

圖1所示的分段式磁致伸縮導(dǎo)波傳感器為非軸對(duì)稱加載的傳感器。鐵鈷條帶預(yù)先磁化，粘貼在待測(cè)管道外表面處，作為導(dǎo)波傳遞的媒介。鐵鈷條帶為高導(dǎo)磁材料，磁致伸縮性能很強(qiáng)，利用鐵鈷條帶中的剩磁作為偏置磁場(chǎng)，易于在磁致伸縮作用下產(chǎn)生振動(dòng)，激發(fā)出超聲導(dǎo)波。非軸對(duì)稱加載的傳感器可激發(fā)出L（m，2）模態(tài)簇，包括L（0，2）模態(tài)及與其相速度相近的F（m，3）彎曲模態(tài)。

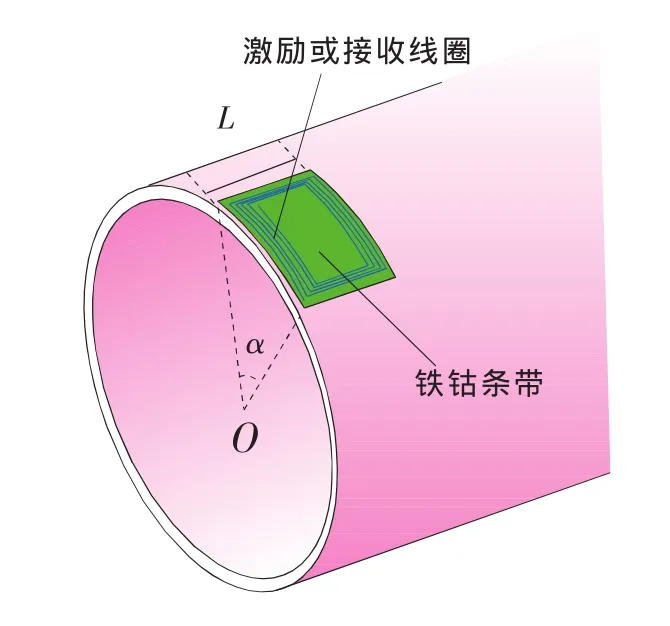
圖1 分段式磁致伸縮導(dǎo)波傳感器示意圖

根據(jù)圖2所示的L（m，2）模態(tài)簇的群速度頻散曲線圖可知，在特定頻率下同時(shí)存在多種模態(tài)的導(dǎo)波，且大都是頻散的。在截止頻率以上時(shí)，L（0，2）模態(tài)的群速度曲線較為水平，F(xiàn)（m，3）模態(tài)的群速度隨頻率不同有較大變化，且隨m的增大，變化程度越大，即頻散程度越嚴(yán)重。頻率為91kHz時(shí)，L（0，2）模態(tài)處于非頻散階段，其他模態(tài)都有一定頻散，且L（0，2）模態(tài)群速度最快，m越大，F(xiàn)（m，3）的群速度越小。

在群速度頻散曲線的基礎(chǔ)上，傳播距離已知時(shí)，根據(jù)t=d/cg可得到各模態(tài)時(shí)間與頻率的關(guān)系，即得到理論上的時(shí)頻曲線。

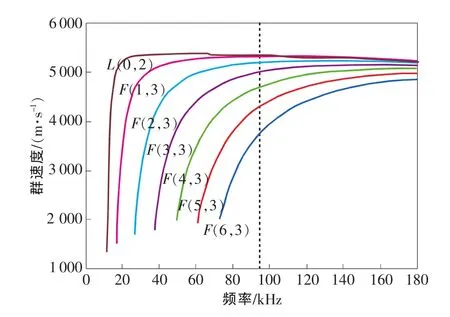
圖2 L（m，2）模態(tài)簇導(dǎo)波群速度頻散曲線

1.2 短時(shí)傅里葉變換

短時(shí)傅里葉變換（STFT）是一種研究非平穩(wěn)信號(hào)的有效手段[7，13]。STFT首先利用一個(gè)形狀光滑的窗函數(shù)ω（t-τ）截取信號(hào)x（t），并假設(shè)截取的信號(hào)是平穩(wěn)信號(hào)，再進(jìn)行傅里葉變換，該過(guò)程可表示為

(一)在總結(jié)歷史經(jīng)驗(yàn)和新鮮經(jīng)驗(yàn)基礎(chǔ)上，對(duì)什么是中國(guó)特色社會(huì)主義道路的內(nèi)涵作了科學(xué)完整的概括，初步明確了中國(guó)特色社會(huì)主義的總體布局

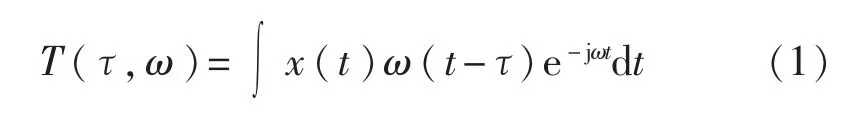
STFT是窗中心所處的時(shí)間和頻率的函數(shù)，能夠表示出導(dǎo)波信號(hào)在時(shí)頻空間的能量分布，物理意義明確，耗時(shí)短，速度快。

導(dǎo)波信號(hào)經(jīng)STFT分析后，與導(dǎo)波理論計(jì)算的時(shí)頻曲線對(duì)照，可以辨認(rèn)出導(dǎo)波波包所對(duì)應(yīng)的模態(tài)，達(dá)到模態(tài)識(shí)別的目的。

1.3 頻散補(bǔ)償原理

導(dǎo)波的多模態(tài)和頻散特性使得難以精確、可靠地評(píng)估管道的缺陷和損傷。由于每個(gè)模態(tài)有各自的波長(zhǎng)和波結(jié)構(gòu)特征，多個(gè)模態(tài)的信號(hào)疊加使得導(dǎo)波信號(hào)較為復(fù)雜。

導(dǎo)波傳播距離為x時(shí)，由于波數(shù)是頻率的函數(shù)，即k=k（ω），造成激勵(lì)信號(hào)在時(shí)域上的變化，可以表示為

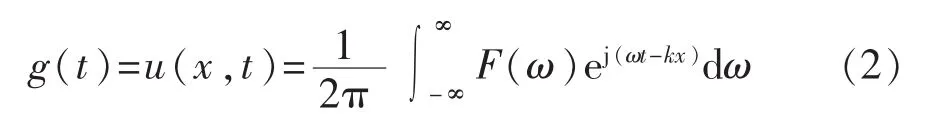
其中F（ω）為激勵(lì)信號(hào)f（t）的傅里葉變換。

由式（2）可知，如果在積分項(xiàng)中乘以ejkx即可抵消頻散的影響，即假設(shè)將導(dǎo)波信號(hào)向后傳播x至激勵(lì)源位置，達(dá)到頻散補(bǔ)償?shù)哪康摹Ｑa(bǔ)償后的導(dǎo)波信號(hào)可以表示為

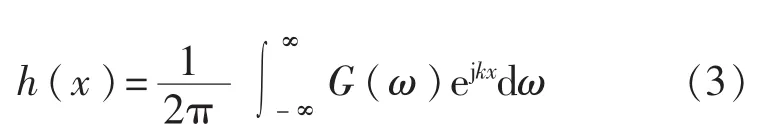
其中G（ω）為導(dǎo)波信號(hào)g（t）的傅里葉變換。

由頻散關(guān)系可知，頻率、群速度和波數(shù)滿足：

帶入式（3）可得：

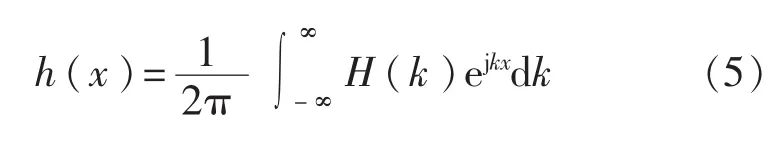
其中H（k）=G（ω）cg（ω），ω=ω（k）。

式（5）為傅里葉逆變換（IFFT），可以將信號(hào)由時(shí)間域轉(zhuǎn)換到空間域。為滿足IFFT的實(shí)用條件，需對(duì)空間-波數(shù)域進(jìn)行插值處理。類似于時(shí)頻域的IFFT，為保證空間域的計(jì)算精度，波數(shù)插值間隔不能太小，具體的方法可參考文獻(xiàn)[8]。

對(duì)各個(gè)模態(tài)頻散補(bǔ)償后的信號(hào)相加可得多模態(tài)頻散補(bǔ)償結(jié)果：

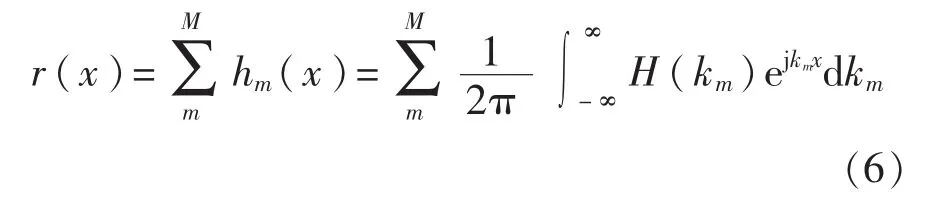
式中：m——模態(tài)編號(hào)；

M——總的模態(tài)數(shù)量。

2 時(shí)頻分析和頻散補(bǔ)償步驟

非對(duì)稱激勵(lì)源可激發(fā)一系列彎曲模態(tài)導(dǎo)波，首先應(yīng)對(duì)各有效模態(tài)進(jìn)行區(qū)分。時(shí)頻分析能夠清晰地描述信號(hào)在任意時(shí)刻的頻率成分，可以用于導(dǎo)波各模態(tài)的識(shí)別。本文采用短時(shí)傅里葉變換法（STFT）進(jìn)行時(shí)頻分析，并對(duì)分離出的各個(gè)模態(tài)導(dǎo)波進(jìn)行頻散補(bǔ)償。

采用時(shí)頻分析識(shí)別模態(tài)并進(jìn)行頻散補(bǔ)償?shù)牟襟E流程為：首先將采集的信號(hào)進(jìn)行時(shí)頻分析（STFT），并計(jì)算與實(shí)驗(yàn)管道相同參數(shù)的頻散曲線和時(shí)間-頻率曲線，然后將時(shí)頻分析圖與計(jì)算的時(shí)間-頻率曲線對(duì)比，確定導(dǎo)波信號(hào)各個(gè)波包的模態(tài)。截取對(duì)應(yīng)模態(tài)的時(shí)域信號(hào)，利用頻散補(bǔ)償算法進(jìn)行補(bǔ)償，最后利用式（6）對(duì)各個(gè)模態(tài)頻散補(bǔ)償后的信號(hào)相加，得到最終的結(jié)果。

3 實(shí)驗(yàn)驗(yàn)證

3.1 實(shí)驗(yàn)裝置

實(shí)驗(yàn)管道材質(zhì)為20#鋼，密度為7800kg/m3，彈性模量為210GPa，泊松比為0.3。管道外徑為159mm，壁厚為4.5mm，刻痕缺陷距離傳感器端2m。采用分段式磁致伸縮導(dǎo)波傳感器，利用鐵鈷條帶中的剩磁作為偏置磁場(chǎng)，并在條帶中激發(fā)超聲導(dǎo)波，條帶粘貼在待測(cè)管道外表面處，作為導(dǎo)波傳遞的媒介。圖3為傳感器布置示意圖，激勵(lì)線圈和接收線圈的周向覆蓋角度為45°，軸向長(zhǎng)度為50 mm，可激發(fā)出沿軸向傳播的L（m，2）導(dǎo)波。

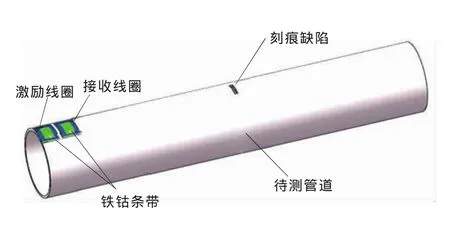
圖3 傳感器布置示意圖

3.2 實(shí)驗(yàn)過(guò)程及結(jié)果

激勵(lì)頻率為91kHz，導(dǎo)波檢測(cè)系統(tǒng)采集的信號(hào)，并按照如前所述的流程進(jìn)行時(shí)頻分析和頻散補(bǔ)償處理。導(dǎo)波信號(hào)如圖4（a）所示，可見(jiàn)刻痕的反射有多個(gè)波包，且比較雜亂，不利于缺陷的軸向定位。對(duì)導(dǎo)波信號(hào)進(jìn)行STFT分析，如圖4（b）所示，與L（0，2）模態(tài)和F（m，3）模態(tài)的時(shí)間-頻率曲線對(duì)比可知，缺陷反射波包主要由L（0，2）、F（4，3）、F（6，3）模態(tài)導(dǎo)波疊加而成。

對(duì)應(yīng)時(shí)域信號(hào)截取相應(yīng)的波包，圖5（a1）、圖5（b1）、圖5（c1）分別為L(zhǎng)（0，2）、F（4，3）、F（6，3）模態(tài)對(duì)應(yīng)的時(shí)域波包，分別按照頻散補(bǔ)償方法進(jìn)行補(bǔ)償處理，其結(jié)果如圖5（a2）、圖5（b2）、圖5（c2）所示，可見(jiàn)補(bǔ)償后的波包中心位置都在4m處，表示出了導(dǎo)波實(shí)際的傳播距離，與缺陷的實(shí)際位置吻合。疊加后的空間域信號(hào)圖5（d2）與時(shí)域信號(hào)圖5（d1）相比，更能清晰地表示缺陷的位置，避免了多模態(tài)導(dǎo)波因頻散引起的定位誤差。

4 結(jié)束語(yǔ)

在管道缺陷檢測(cè)時(shí)，非對(duì)稱加載的導(dǎo)波傳感器可激發(fā)出多種模態(tài)的導(dǎo)波，對(duì)缺陷的識(shí)別和定位產(chǎn)生干擾，限制了彎曲模態(tài)導(dǎo)波的應(yīng)用。本文研究了彎曲導(dǎo)波模態(tài)分離和頻散補(bǔ)償方法，并通過(guò)實(shí)驗(yàn)驗(yàn)證了該方法的有效性。研究結(jié)果表明：

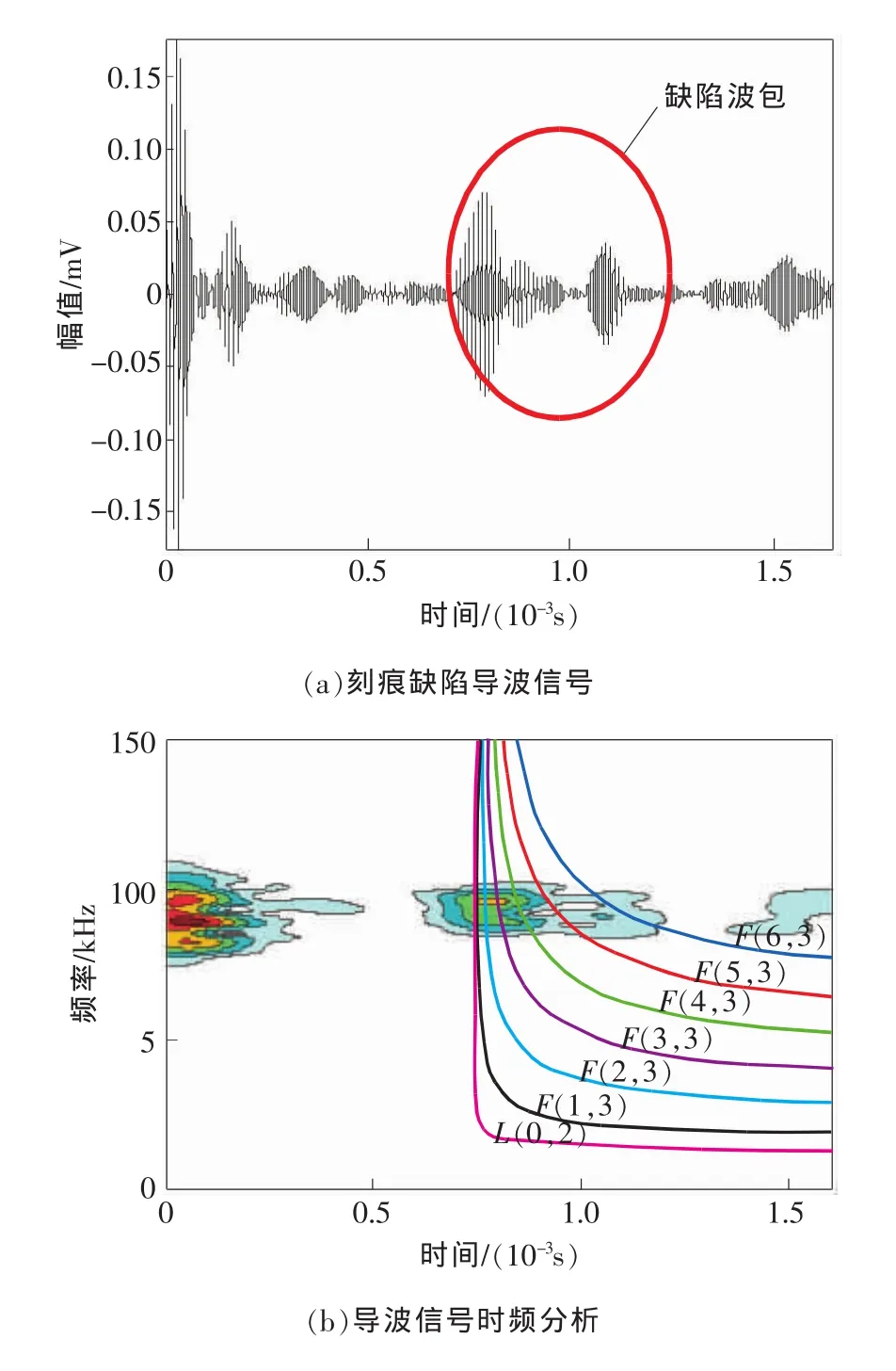
圖4 未進(jìn)行補(bǔ)償?shù)膶?dǎo)波時(shí)域信號(hào)和時(shí)頻分析

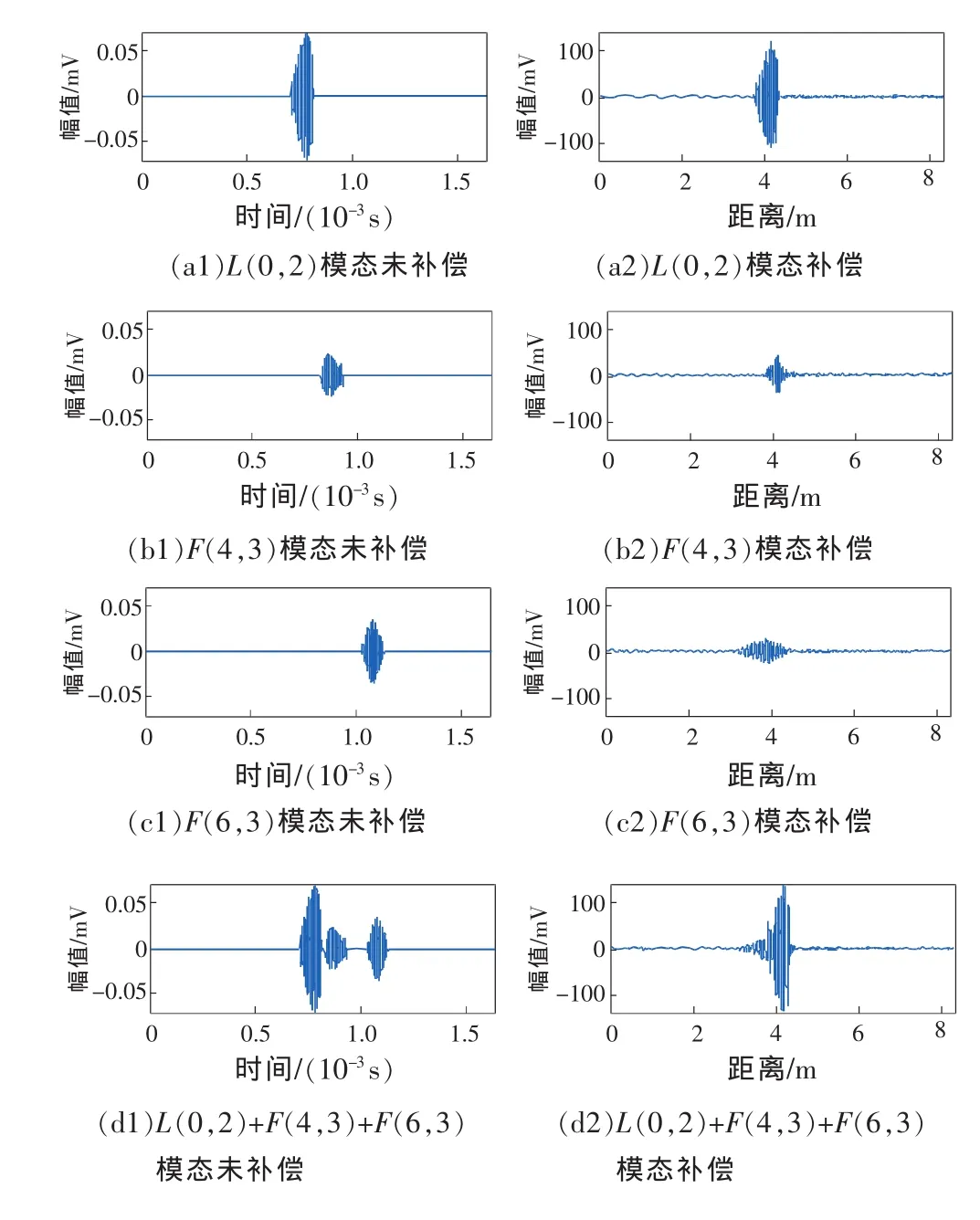
圖5 缺陷反射波包各模態(tài)頻散補(bǔ)償前后對(duì)比

1）利用STFT進(jìn)行時(shí)頻分析可以表示出導(dǎo)波時(shí)頻空間的能量分布特征，與理論計(jì)算的時(shí)頻曲線對(duì)比，可以有效識(shí)別出導(dǎo)波的各個(gè)模態(tài)。

2）對(duì)各個(gè)模態(tài)導(dǎo)波信號(hào)進(jìn)行頻散補(bǔ)償處理后，消除了頻散效應(yīng)的影響，各個(gè)模態(tài)波包能夠與導(dǎo)波實(shí)際傳播距離相對(duì)應(yīng)，缺陷定位更精確。

[1]陳志奎，賈少攀，趙亮，等.基于物聯(lián)網(wǎng)和超聲導(dǎo)波的管道檢測(cè)系統(tǒng)研究[J].中國(guó)測(cè)試，2013，39（2）：94-97.

[2]王悅民，謝俊麗，劉東，等.基于磁致伸縮效應(yīng)的導(dǎo)波無(wú)損檢測(cè)技術(shù)研究進(jìn)展[J].無(wú)損檢測(cè)，2007，29（5）：280-284.

[3]苗曉婷.基于導(dǎo)波的結(jié)構(gòu)健康監(jiān)測(cè)中特征提取技術(shù)與損傷識(shí)別方法的研究[D].上海：上海交通大學(xué)，2011.

[4]SHIN H J，ROSE J L.Guided waves by axisymmetric and non-axisymmetric surface loading on hollow cylinders[J].Ultrasonics，1999，37（5）：355-363.

[5]EVERY A G，SHATALOV M Y，YENWONG-FAI A S. Progress in the analysis of non-axisymmetric wave propagation in a homogeneous solid circular cylinder of a piezoelectric transversely isotropic material[J].Physics Procedia，2010，3（1）：473-479.

[6]他得安，劉鎮(zhèn)清.超聲無(wú)損檢測(cè)中的二維快速Fourier變換及Wigner-Ville變換[J].無(wú)損檢測(cè)，2001，23（7）：313-316.

[7]周正干，馮占英，高翌飛，等.時(shí)頻分析在超聲導(dǎo)波信號(hào)分析中的應(yīng)用[J].北京航空航天大學(xué)學(xué)報(bào)，2008，34（7）：833-837.

[8]WILCOX P D.A rapid signal processing technique to remove the effect of dispersion from guided wave signals[J]. IEEE Transactions on Ultrasonics Ferroelectrics&Frequency Control，2003，50（4）：419-427.

[9]FINK M.Time reversal of ultrasonic fields.I.Basic principles[J].IEEE Transactions on Ultrasonics Ferroelectrics&Frequency Control，1992，39（5）：555-566.

[10]ING R K，F(xiàn)INK M.Self-focusing and time recompression of Lamb waves using a time reversal mirror[J].Ultrasonics，1998，36（1）：179-186.

[11]ZENG L，LIN J，LEI Y，et al.Waveform design for high-resolution damage detection using lamb waves[J]. IEEE Transactions on Ultrasonics Ferroelectrics&Frequency Control，2013，60（5）：1025-1029.

[12]LIU L，YUAN F G.A linear mapping technique for dispersion removal of Lamb waves[J].Structural Health Monitoring，2010，9（1）：75-86.

[13]孫雅欣，吳斌，何存富，等.時(shí)頻分析在桿中導(dǎo)波傳播特性研究中的應(yīng)用[J].儀器儀表學(xué)報(bào)，2006，27（z2）：1316-1317.

（編輯：李妮）

Research on mode separation and dispersion compensation of flexural mode guided wave

CHEN Le，WANG Yuemin，GENG Haiquan，YE Wei，DENG Wenli
（College of Power Engineering，Naval University of Engineering，Wuhan 430033，China）

In order to reduce the adverse effects of multi-modality and dispersion characteristics of ultrasonic guided wave signal on the detection of pipeline defects，the methods of flexural guided wave mode separation and dispersion compensation are studied.Firstly，the guide wave signal frequency analysis and theoretical calculation of frequency curve were compared to determine the signal of each modal，and then the signal of each modal was processed by dispersive compensation algorithm;Finally，the final results were obtained by adding the compensated signals.From the pipeline defect detection experiment results，it can be seen:multiple wave packets caused by multi-modal and frequency dispersion characteristics can be identified by STFT method and each wavepacketcan correspond tothesamedefectposition afterdispersion compensation.The experimental results show that the guided wave signal is more conducive to the identification and localization of the defects after the modal identification，separation and dispersion compensation，and the method provides a theoretical basis for the application of flexural guided wave.

ultrasonic guided wave；time frequency analysis；mode separation；dispersion compensation；defect localization

A

：1674-5124（2016）12-0132-04

10.11857/j.issn.1674-5124.2016.12.027

2016-06-13；

：2016-07-28

總裝備部裝備預(yù)研基金項(xiàng)目（9140A27020115JB11001）

陳 樂(lè)（1986-），男，山東淄博市人，博士研究生，研究方向?yàn)閷?dǎo)波無(wú)損檢測(cè)技術(shù)。