負(fù)泊松比負(fù)熱膨脹超材料微結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計

王 昱, 呂恩利, 王亞娟, 王飛仁, 林小娟

(華南農(nóng)業(yè)大學(xué) 工程學(xué)院,廣州 510642)

負(fù)泊松比負(fù)熱膨脹超材料微結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計

王 昱, 呂恩利, 王亞娟, 王飛仁, 林小娟

(華南農(nóng)業(yè)大學(xué) 工程學(xué)院,廣州 510642)

提出一種拓?fù)鋬?yōu)化設(shè)計方法,用于設(shè)計同時具有負(fù)泊松比和負(fù)熱膨脹系數(shù)的超材料.超材料是人工設(shè)計的復(fù)合材料,由微米或納米結(jié)構(gòu)的周期性陣列組成,并具有天然材料難以具備的超常物理性質(zhì).基于拓?fù)鋬?yōu)化理論,建立了一個表示多材料微觀結(jié)構(gòu)的多相邊界的水平集模型,并采用數(shù)值均勻化方法來計算微觀結(jié)構(gòu)的等效性能,然后通過參數(shù)化水平集優(yōu)化方法實現(xiàn)邊界形狀的演變和拓?fù)浣Y(jié)構(gòu)的設(shè)計.通過兩個數(shù)值算例,給出超材料微結(jié)構(gòu)材料分布的優(yōu)化結(jié)果,證明了設(shè)計方法的可行性,為實現(xiàn)具備特殊性能的人工材料設(shè)計提供了一套系統(tǒng)的設(shè)計方法.

超材料; 拓?fù)鋬?yōu)化; 水平集方法; 負(fù)泊松比; 負(fù)熱膨脹

在工程應(yīng)用中,溫度變化會引起尺寸變化,所以必須考慮材料和結(jié)構(gòu)的膨脹與收縮.由于大多數(shù)材料的應(yīng)用環(huán)境將經(jīng)歷一系列的工作溫度,無論是技術(shù)還是基礎(chǔ)研究領(lǐng)域都會關(guān)注由溫度變化引起的結(jié)構(gòu)的熱膨脹[10].熱膨脹系數(shù)是一個重要的物理量,用來測量溫度對材料尺寸的改變程度.負(fù)熱膨脹材料(NTE)在一定的溫度升高范圍內(nèi)呈現(xiàn)收縮的熱彈性能.相關(guān)研究證明,由三相材料組成的復(fù)合材料的性能可以超越其中單相材料的性能[11].因此,極端的熱彈性能的材料通常是通過組合三相傳統(tǒng)的材料,如金屬或塑料等,得到一個新的具有周期結(jié)構(gòu)的復(fù)合材料.

泊松比[1]被定義為在單軸拉伸條件下,橫向收縮應(yīng)變與縱向拉伸應(yīng)變的比值,這是衡量彈性材料性能的基本指標(biāo).彈性理論允許泊松比為負(fù),但大多數(shù)傳統(tǒng)材料泊松比為正.與正泊松比的常規(guī)材料相比,具有負(fù)泊松比的材料(NPR)表現(xiàn)出非常規(guī)的屬性,即橫向拉伸時縱向膨脹,橫向收縮時縱向壓縮.由于廣泛的應(yīng)用潛力,自從早期研究工作以來[12],負(fù)泊松比材料已經(jīng)吸引了越來越多的關(guān)注.到目前為止,已有一些方法開發(fā)設(shè)計拉脹材料[13-15],但鮮有系統(tǒng)的設(shè)計方法用于設(shè)計同時表現(xiàn)NPR和NTE的超材料.

拓?fù)鋬?yōu)化已被確定為是在結(jié)構(gòu)優(yōu)化領(lǐng)域最有前途的技術(shù)之一[16],其中,水平集方法因其具有光滑的設(shè)計邊界,并集成了形狀優(yōu)化和拓?fù)鋬?yōu)化,已經(jīng)成為一種備受關(guān)注的形狀結(jié)構(gòu)拓?fù)鋬?yōu)化方法.特別是參數(shù)化水平集方法(PLSM)[17],已被證明是一個最強大的主流拓?fù)湫螤顑?yōu)化的結(jié)構(gòu)和機制.它能很好地繼承傳統(tǒng)水平集方法的優(yōu)點,并使許多有效的基于梯度的優(yōu)化算法[18]直接應(yīng)用到水平集方法中[19].

因此,本文基于多相水平集模型來設(shè)計同時具有NPR和NTE的超材料拓?fù)湫螤?多相水平集模型是一個顯示多材料的邊界的水平集函數(shù),該函數(shù)能避免設(shè)計域出現(xiàn)材料重疊與空白.文中還將采用基于PLSM的超材料微結(jié)構(gòu)設(shè)計方法.在這種方法中,應(yīng)用了數(shù)值均勻化方法來計算復(fù)合材料的宏觀等效性能,并使用PLSM來實現(xiàn)形狀和多材料微結(jié)構(gòu)拓?fù)溲葑?最后,通過兩個典型的數(shù)值算例證明所提出方法的有效性.

1 拓?fù)鋬?yōu)化方法

1.1 參數(shù)化水平集方法

在水平集方法(LSM)方法中,設(shè)計邊界通過高維水平集函數(shù)的零水平集形成的隱式邊界表達(dá)[20-21].一個水平集函數(shù)Φ(x)要求在參考域D內(nèi)具有Lipschitz連續(xù)性.對于本文涉及的多相材料設(shè)計問題,采用m個水平集函數(shù)相結(jié)合來描述m+1相材料,包括無材料相(即孔洞)和m相固體材料.固體材料、邊界及孔洞的水平集表達(dá)式分別為

(1)

式中:I=1,…,m為某一水平集函數(shù);m是水平集函數(shù)的總數(shù);D為設(shè)計參考域,包括所有允許的微觀結(jié)構(gòu)的形狀;ΩI是函數(shù)值為正的水平集函數(shù);?ΩI表示第I個水平集函數(shù)的設(shè)計邊界.

我最喜歡的蔬菜是西紅柿。西紅柿圓圓的，像個小燈籠似的。它的顏色各異：有的是粉色的，上面還隱隱約約的白點，媽媽說這樣的西紅柿是沙瓤的，吃起來更美味；有的是紅紅的，像是小姑娘羞紅了的臉蛋，越看越可愛，我都有點不舍得吃了；還有黃綠相間的西紅柿，據(jù)說是科學(xué)家叔叔們發(fā)明的新品種，聞起來有股淡淡的清香，吃起來酸甜可口，味道純正，科學(xué)家叔叔們真了不起！

在PLSM方法中,采用緊支徑向基函數(shù)(CS-RBF)插值得到高維水平集函數(shù),有利于平衡插值精度和效率.原來的水平集函數(shù)可以用CS-RBF在預(yù)先指定節(jié)點的插值表達(dá),即

形狀函數(shù)向量為

(3)

擴展系數(shù)向量為

(4)

式中:N是設(shè)計域內(nèi)CS-RBF節(jié)點總數(shù);t為虛擬時間.

通過CS-RBFs插值可實現(xiàn)時間和空間的分離:形狀函數(shù)為空間函數(shù),膨脹系數(shù)僅與時間相關(guān).值得注意的是,用于插值每個隱式水平集函數(shù)的CS-RBFs是相同的.因此,解耦漢密爾頓-雅各比偏微分方程(H-J PDE)的時間相和空間相可得

(5)

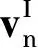
(6)

由式(6)可知,正速度矢量所涉及的項都是通過設(shè)計域內(nèi)的節(jié)點求得,因此正速度擴展到了整個設(shè)計領(lǐng)域.這樣,基于偏微分方程的水平集方程已轉(zhuǎn)化為代數(shù)方程.優(yōu)化唯一的未知數(shù)是插值的膨脹系數(shù),在優(yōu)化設(shè)計中定義為設(shè)計變量,并使用更高效的優(yōu)化算法進(jìn)行迭代.

1.2 三相復(fù)合材料的材料模型

通過材料模型[5],在設(shè)計域內(nèi)的任何計算點x的彈性常數(shù)C和熱應(yīng)變系數(shù)α可以由兩個水平集函數(shù)Φ1和Φ2計算得出.

(7)

(8)

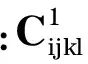
1.3 超材料微結(jié)構(gòu)的形狀拓?fù)鋬?yōu)化

將在給定的設(shè)計域,單胞Y,進(jìn)行形狀拓?fù)鋬?yōu)化.復(fù)合材料的等效彈性張量和熱彈系數(shù)采用均勻化方法計算,得

(9)

(10)

(11)

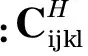
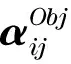
(12)

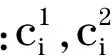
(13)

由于水平集函數(shù)的參數(shù)化,許多更高效的基于梯度的優(yōu)化算法可用于求解優(yōu)化問題,例如:移動漸近線法(MMA)[18].采用MMA需要提供目標(biāo)函數(shù)和約束條件的關(guān)于設(shè)計變量的一階導(dǎo)數(shù).目標(biāo)函數(shù)關(guān)于設(shè)計變量的一階導(dǎo)數(shù)表示為

其中,

式中:χij為位移場;αpq為局部熱應(yīng)變場.

體積約束相對于設(shè)計變量的導(dǎo)數(shù)為

(18)

式中,δ為狄拉克函數(shù),是Heaviside函數(shù)的一階導(dǎo)數(shù).

2 數(shù)值算例

用來計算位移場,設(shè)計域采用4個節(jié)點的四邊形單元離散,且水平集的節(jié)點與四邊形單元的節(jié)點一致.優(yōu)化過程中,水平集函數(shù)采用MMA方法更新設(shè)計變量.收斂準(zhǔn)則為連續(xù)兩次迭代的目標(biāo)函數(shù)值差小于10-4,或最大迭代次數(shù)達(dá)到200次(基于數(shù)值試驗).設(shè)定兩相虛擬固體材料的彈性模量:E1=E2=1;泊松比:v1=v2=0.3;熱膨脹系數(shù):α1=1,α2=10.

2.1 算例1

算例1設(shè)計了一種正交各向異性材料,以實現(xiàn)負(fù)的泊松比(-0.5),以及其在垂直方向上的負(fù)熱應(yīng)變系數(shù)(-0.3).兩相固體材料體積分?jǐn)?shù)分別為0.3和0.1.拓?fù)湫螤畹难莼褪諗窟^程如圖1所示.紅色區(qū)域表示固體材料相1,藍(lán)色區(qū)域表示固體材料相2,而白色區(qū)域是孔洞.兩個水平集的表面和對應(yīng)于所得到的拓?fù)浣Y(jié)構(gòu)的兩個固相的零水平集輪廓.式(19)為優(yōu)化所得彈性張量與熱膨脹系數(shù).

(19)

由式(19)可知,優(yōu)化后材料的泊松比為-0.446 3,垂直方向熱應(yīng)變系數(shù)為-0.261 6.

從算例1的迭代過程可以注意到,形狀拓?fù)鋬?yōu)化設(shè)計方法的特點是擁有光滑的材料邊界和明顯的界線[20-21].此外,在優(yōu)化過程中,所提出的方法不僅可以合并初始設(shè)計中的孔洞,也可以創(chuàng)建新的孔洞,以實現(xiàn)最佳的拓?fù)浣Y(jié)構(gòu)的基本單元.基于所得到的最優(yōu)設(shè)計(如圖2所示),注意到所得的微結(jié)構(gòu)的拓?fù)浣Y(jié)構(gòu)與文獻(xiàn)[9]所獲得的結(jié)果相似.可知等效的彈性和熱彈性能是依賴于施加的負(fù)載后單胞的內(nèi)部結(jié)構(gòu)和變形的方式.因此,設(shè)計一種具有極限性能的復(fù)合材料,微結(jié)構(gòu)的設(shè)計將會出現(xiàn)類似旋轉(zhuǎn)剛性機構(gòu)[1-2]的結(jié)構(gòu).

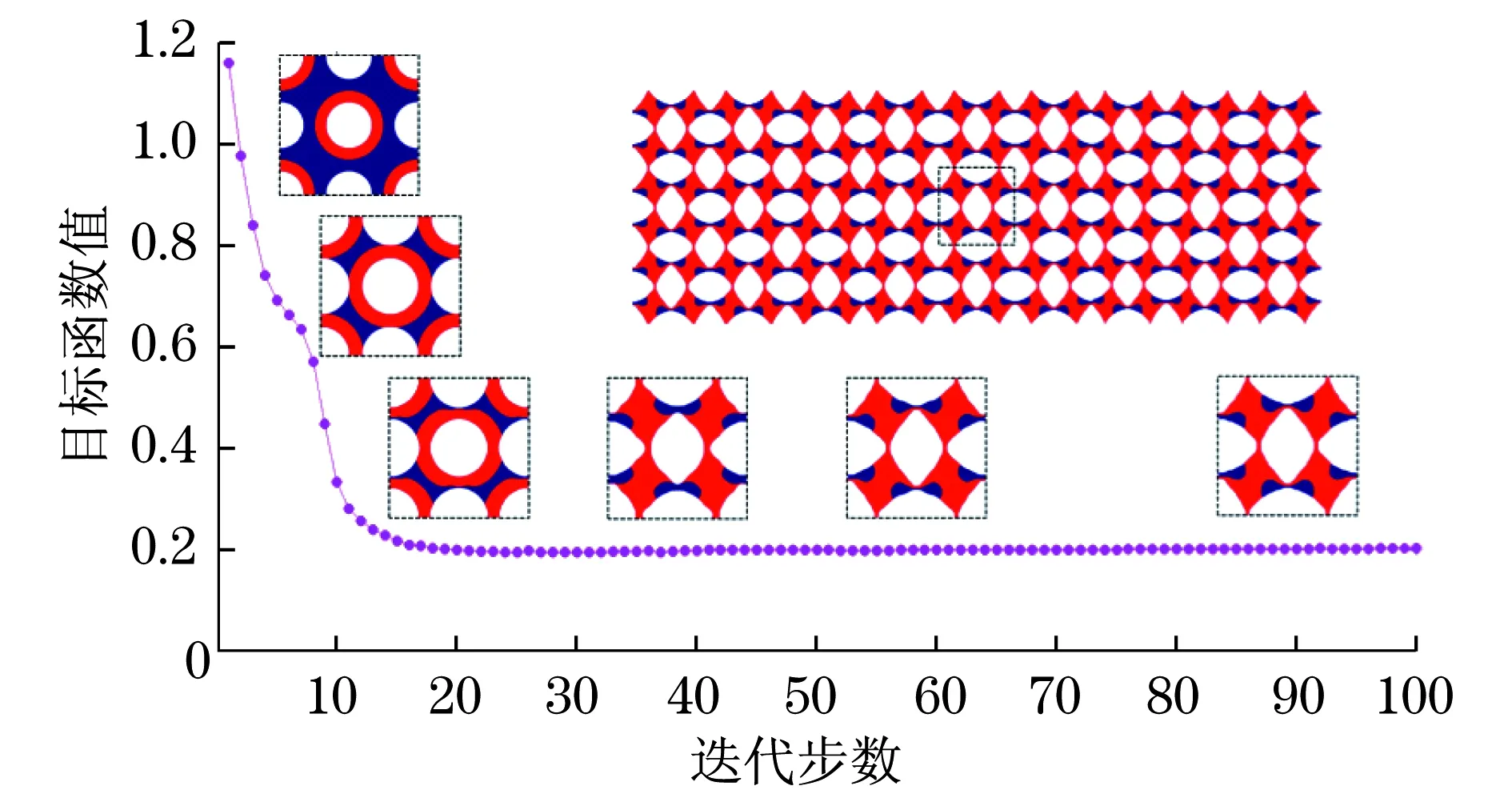
圖1 目標(biāo)函數(shù)的收斂過程(算例1)

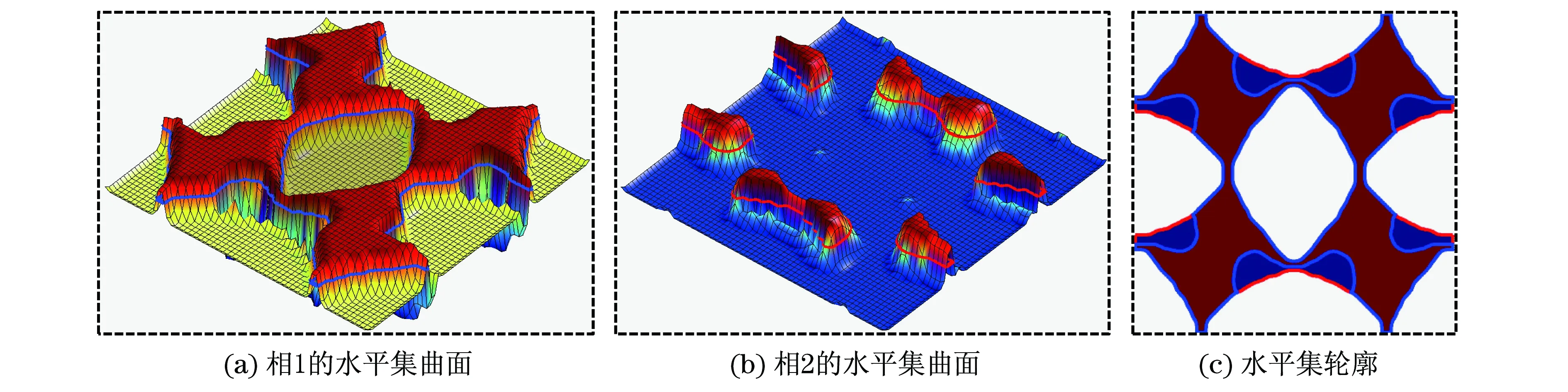
圖2 固體材料相輪廓圖(算例1)

2.2 算例2

算例2設(shè)計了一個正交各向異性材料,以實現(xiàn)負(fù)的泊松比(-0.65),以及在水平方向上的負(fù)熱應(yīng)變系數(shù),且熱應(yīng)變系數(shù)達(dá)到極小值.兩相固體材料體積分?jǐn)?shù)分別為0.25和0.10.拓?fù)湫螤畹难莼褪諗窟^程如圖3所示,式(20)為優(yōu)化所得彈性張量.

(20)

由式(20)可知,優(yōu)化后材料的泊松比為-0.644 2,水平方向熱應(yīng)變系數(shù)為-3.356.

式(20)結(jié)果表明,極端的熱膨脹的形成會導(dǎo)致一個非常低的結(jié)構(gòu)剛度,即實現(xiàn)一個方向的極端熱應(yīng)變將導(dǎo)致在另一個方向上的一個極端的剛度.因此,在一個特定的方向設(shè)計極端熱膨脹材料,應(yīng)在優(yōu)化約束中定義另一方向上的最小剛度值,使設(shè)計具有物理意義.在算例2中,設(shè)定垂直方向的體積模量的下限為0.09.

材料的等效彈性和熱彈性能取決于基本單元的內(nèi)部結(jié)構(gòu)和變形方式,為使微結(jié)構(gòu)在加載時發(fā)生旋轉(zhuǎn),凹角結(jié)構(gòu)的生成是使結(jié)構(gòu)發(fā)生較大旋轉(zhuǎn)效果的關(guān)鍵.在微結(jié)構(gòu)的特定布局下,可以通過類似旋轉(zhuǎn)剛性機構(gòu)的微結(jié)構(gòu)基本單元之間的角度變化,使多孔復(fù)合材料整體變形,達(dá)到負(fù)的極端力學(xué)性能指數(shù),即

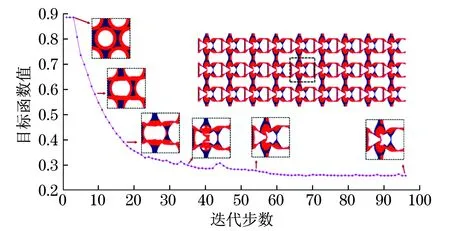
圖3 目標(biāo)函數(shù)的收斂過程(算例2)

負(fù)泊松比和負(fù)熱膨脹系數(shù).在上述兩個數(shù)值例子中,可發(fā)現(xiàn)最佳的泊松比和熱應(yīng)變系數(shù)不能準(zhǔn)確地接近規(guī)定的值.由于拓?fù)湫螤顑?yōu)化最初是連續(xù)體結(jié)構(gòu)的一種設(shè)計方法,它實際上是利用結(jié)構(gòu)的變形來近似模擬剛體的旋轉(zhuǎn)效應(yīng),因此難以使微結(jié)構(gòu)實現(xiàn)如剛性連桿機構(gòu)般的旋轉(zhuǎn)變形.在優(yōu)化過程中會發(fā)生在折返結(jié)構(gòu)部分的類似鉸鏈結(jié)構(gòu)斷開的現(xiàn)象,為保證優(yōu)化所得的結(jié)果為連續(xù)體結(jié)構(gòu),所得結(jié)果無法準(zhǔn)確地達(dá)到設(shè)定的泊松比和熱應(yīng)變系數(shù).盡管如此,該方法仍然提供了一個系統(tǒng)的復(fù)合材料微結(jié)構(gòu)設(shè)計方法,使材料同時達(dá)到預(yù)期的負(fù)泊松比和負(fù)熱膨脹系數(shù).

圖4 固體材料相輪廓圖(算例2)

3 結(jié) 論

利用數(shù)值均勻化方法和參數(shù)化的水平集方法,提出了同時具有NPR和NTE性質(zhì)復(fù)合材料的系統(tǒng)設(shè)計方法.數(shù)值算例的結(jié)果驗證了所提出的拓?fù)湫螤钤O(shè)計方法的有效性.材料微結(jié)構(gòu)設(shè)計可以從二維推廣到三維,但計算成本將顯著增加.同時,該方法具有拓展至其他類型超材料設(shè)計的潛力.

[1] EVANS K E,ALDERSON A.Auxetic materials:functional materials and structures from lateral thinking![J].Advanced Materials,2000,12(9):617-628.

[2] LAKES R.Cellular solid structures with unbounded thermal expansion[J].Journal of Materials Science Letters,1996,15(6):475-477.

[3] GAO Y,ZHOU N,YANG F,et al.P-phase precipitation and its effect on martensitic transformation in (Ni,Pt)Ti shape memory alloys[J].Acta Materialia,2012,60(4):1514-1527.[4] GAO Y,ZHOU N,WANG D,et al.Pattern formation during cubic to orthorhombic martensitic transformations in shape memory alloys[J].Acta Materialia,2014,68:93-105.

[5] SIGMUND O.A new class of extremal composites[J].Journal of the Mechanics and Physics of Solids,2000,48(2):397-428.

[6] GUEST J K,PRéVOST J H.Design of maximum permeability material structures[J].Computer Methods in Applied Mechanics and Engineering,2007,196(4/5/6):1006-1017.

[7] 張衛(wèi)紅,汪雷,孫士平.基于導(dǎo)熱性能的復(fù)合材料微結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計[J].航空學(xué)報,2006,27(6):1229-1233.

[8] 孫士平,張衛(wèi)紅.多相材料微結(jié)構(gòu)多目標(biāo)拓?fù)鋬?yōu)化設(shè)計[J].力學(xué)學(xué)報,2006,38(5):633-638.

[9] 孫良奎,于哲峰,黃潔.基于超材料的平板二維定向傳熱結(jié)構(gòu)設(shè)計[J].物理學(xué)報,2015,64(22):0224401.

[10] SIGMUND O,TORQUATO S.Composites with extremal thermal expansion coefficients[J].Applied Physics Letters,1996,69(21):3203-3205.

[11] LAKES R.Materials with structural hierarchy[J].Nature,1993,361(6412):511-515.

[12] LAKES R.Foam structures with a negative Poisson's ratio[J].Science,1987,235(4792):1038-1040.

[13] YANG W,LI Z M,SHI W,et al.Review on auxetic materials[J].Journal of Materials Science,2004,39(10):3269-3279.

[14] 曹先凡,劉書田.基于拓?fù)涿枋龊瘮?shù)的特定性能材料設(shè)計方法[J].固體力學(xué)學(xué)報,2006,27(3):217-222.

[15] 宋迎東,孫杰,孫志剛,等.基于遺傳算法的復(fù)合材料細(xì)觀結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計[J].固體力學(xué)學(xué)報,2009,30(4):416-423.

[16] BENDSOE M P,SIGMUND O.Topology optimization:theory,methods and applications[M].Berlin Heidelberg:Springer-Verlag,2004.

[17] LUO Z,TONG L Y,WANG M Y,et al.Shape and topology optimization of compliant mechanisms using a parameterization level set method[J].Journal of Computational Physics,2007,227(1):680-705.

[18] SVANBERG K.The method of moving asymptotes—a new method for structural optimization[J].International Journal for Numerical Methods in Engineering,1987,24(2):359-373.

[19] BELYTSCHKO T,XIAO S P,PARIMI C.Topology optimization with implicit functions and regularization[J].International Journal for Numerical Methods in Engineering,2003,57(8):1177-1196.

[20] ALLAIRE G,JOUVE F,TOADER A M.Structural optimization using sensitivity analysis and a level-set method[J].Journal of Computational Physics,2004,194(1):363-393.

[21] WANG M Y,WANG X M,GUO D M.A level set method for structural topology optimization[J].Computer Methods in Applied Mechanics and Engineering,2003,192(1/2):227-246.

(編輯:丁紅藝)

Topology Optimization Design of Microstructured Metamaterials with Negative Poisson’s Ratio and Negative Thermal Expansion

WANG Yu, Lü Enli, WANG Yajuan, WANG Feiren, LIN Xiaojuan

(CollegeofEngineering,SouthChinaAgriculturalUniversity,Guangzhou510642,China)

A level set-based method was introduced to design the metamaterials which can exhibit negative Poisson’s ratio and negative thermal expansion simultaneously.Negative Poisson’s ratio (also called auxeticity) and negative thermal expansion are phenomena that may rarely be found in the nature materials.It is now known that these unusual properties are mainly dependent on the particular features in the material’s micro- or nano- structural deformation when subjected to a thermal or mechanical load.A numerical homogenization method was applied to evaluate the effective properties of the microstructure,and the multi-phase level set method was used to implement the shape and topology evolutions of the microstructure.Two numerical examples were given to demonstrate the feasibility of the proposed topology optimization method,which provides a systematic design method for the design of artificial materials with special properties.

metamaterial;topologicalshapeoptimization;letsetmethod;negativePoisson’sratio;negativethermalexpansion

1007-6735(2016)06-0551-06

10.13255/j.cnki.jusst.2016.06.008

2016-09-08

廣東省農(nóng)產(chǎn)品冷鏈物流裝備工程技術(shù)研究中心建設(shè)項目(2016B090920092);華南農(nóng)業(yè)大學(xué)高水平青年科技人才培育基金項目(216262)

王 昱(1987-),女,講師.研究方向:結(jié)構(gòu)拓?fù)鋬?yōu)化、汽車輕量化設(shè)計等.E-mail:yu-wang@scau.edu.cn

呂恩利(1979-),男,教授.研究方向:果蔬冷鏈物流技術(shù)與裝備、交通運輸、汽車維修檢測等.E-mail:enlilv@scau.edu.cn

TH 122

A