波形鋼腹板PC箱梁橋的車橋耦合振動分析及動力沖擊系數計算①

冀 偉， 鄧 露， 何 維

(1.蘭州交通大學土木工程學院，甘肅 蘭州 730070；2.湖南大學土木工程學院，湖南 長沙 410082)

波形鋼腹板PC箱梁橋的車橋耦合振動分析及動力沖擊系數計算①

冀 偉1， 鄧 露2， 何 維2

(1.蘭州交通大學土木工程學院，甘肅 蘭州 730070；2.湖南大學土木工程學院，湖南 長沙 410082)

為了科學合理地確定波形鋼腹板PC簡支箱梁橋的動力沖擊系數，依據標準車輛的車輪與橋面的接觸關系建立了車-橋系統耦合振動的動力方程。在考慮路面平整度隨機激勵的作用下，運用MATLAB軟件編寫了車橋耦合系統動力方程的求解程序，求得了波形鋼腹板PC簡支箱梁橋結點位移的振動響應，并進一步計算出了該橋型動力沖擊系數的數值解。將求得的數值解與現行《公路橋涵設計通用規范》(JTG D60-2015)中動力沖擊系數的規范值和文中提出的波形鋼腹板PC簡支箱梁橋基頻計算公式求得橋梁基頻后獲取的動力沖擊系數進行對比分析。結果表明：在路面平整度為中的情況下，按照文中提出的波形鋼腹板PC簡支箱梁橋基頻計算公式在獲取橋梁基頻后求得的動力沖擊系數，與JTG D60-2015規范中采用有限元法獲取橋梁結構基頻后求得的動力沖擊系數以及與車橋耦合振動數值模擬獲得的動力沖擊系數值吻合良好，而與JTG D60-2015規范中給出的簡支梁橋基頻估算公式獲取橋梁基頻后求得的動力沖擊系數有較大差異。

車橋耦合振動； 波形鋼腹板； 組合箱梁； 振動頻率； 動力沖擊系數

1 概 述

波形鋼腹板PC箱梁橋是一種新型的鋼-混組合結構橋梁，該橋型充分發揮了混凝土材料和鋼材兩者的性能，即混凝土抗彎，波形鋼腹板抗剪，結構受力非常合理[1]，同時該橋型在減輕橋梁自重，提高預應力施加效率方面也具有顯著的優點，因此其已在國內外的橋梁工程中得到了廣泛應用。

近年來國外學者主要對波形鋼板和波形鋼腹板I型鋼梁的抗彎、抗剪和屈曲性能方面[2-5]進行了研究，而國內學者的研究則主要集中在剪力滯效應[6]、撓度計算[7-8]、抗彎[9]及抗扭性能[9-10]等方面。國內外學者對在移動車輛作用下的波形鋼腹板PC箱梁橋動力響應和動力沖擊系數的研究相對較少。

動力沖擊系數(IM)是橋梁設計中用以表征車輛通過橋梁時對橋梁產生的豎向動力效應增大系數，是橋梁設計中的一個非常重要的指標，也是進行橋梁狀況評估的一個重要參數，其定義為

(1)

式中Zdmax為最大動位移，Zsmax為最大靜位移。

中國現行《公路橋涵設計通用規范》(JTG D60-2015，以下簡稱15規范)[11]中采用橋梁基頻來計算其動力沖擊系數，但已有研究表明采用現行15規范中的橋梁基頻公式計算波形鋼腹板PC箱梁橋的基頻與實際結構的基頻存在著較大差異[12]，而采用精細三維有限元法計算其基頻又存在建模復雜、通用性差的問題；再者15規范中基頻與沖擊系數之間的關系是通過實測7座橋梁(跨徑6 m的鋼筋混凝土矩形板橋到跨徑45 m的預應力混凝土箱梁橋)的動力響應，并對測得的數據進行回歸分析和適當修正后得到沖擊系數的計算公式，但該公式是否適用于波形鋼腹板PC箱梁橋這一特殊橋型還需進一步研究。文獻[13]以一座裝配式波形鋼腹板PC連續箱梁橋潑河大橋為工程背景，對該橋的動力沖擊系數進行了研究，但是文中僅對該橋的動力沖擊系數進行了影響參數分析，對該類型橋梁動力沖擊系數合理取值問題并未做進一步的研究。

針對以上研究現狀和存在的問題，本文基于車橋耦合振動理論，利用數值模擬技術計算了跨徑為30 m的單箱單室波形鋼腹板PC簡支箱梁橋在移動車輛荷載作用下的動力沖擊系數，并對行駛速度和路面平整度等多個影響動力沖擊系數的因素進行了分析。最后將沖擊系數的計算結果與15規范中定義的規范值進行比較以考察規范定義的動力沖擊系數的合理性，并得到一些有意義的結論，這些結論可以為中國波形鋼腹板PC箱梁橋動力沖擊系數的確定提供參考。

2 標準車輛模型的建立

移動車輛的類型、軸數、軸重和車輛基頻等參數對橋梁動力沖擊系數有不同程度的影響，本文選用國內外學者在車橋耦合振動研究中常采用的兩軸車和三軸車模型[14-15]。這兩種車輛模型的詳細參數見表1所示，車輛的幾何示意圖如圖1，2所示。

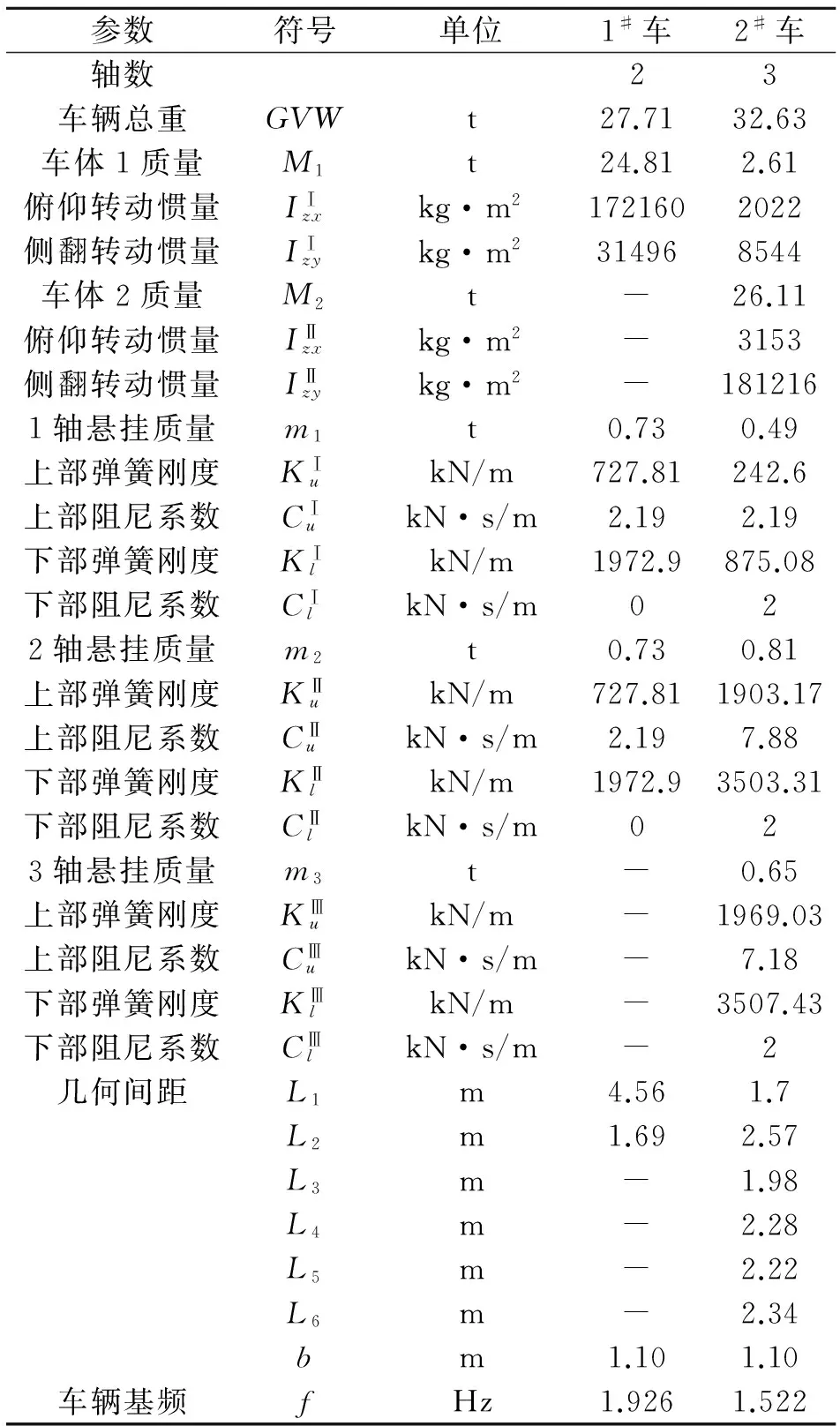
表1 兩種車型的詳細參數

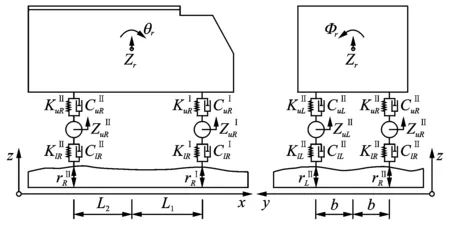
圖1 兩軸車輛模型示意圖Fig.1 Schematic diagram of 2-axle vehicle model

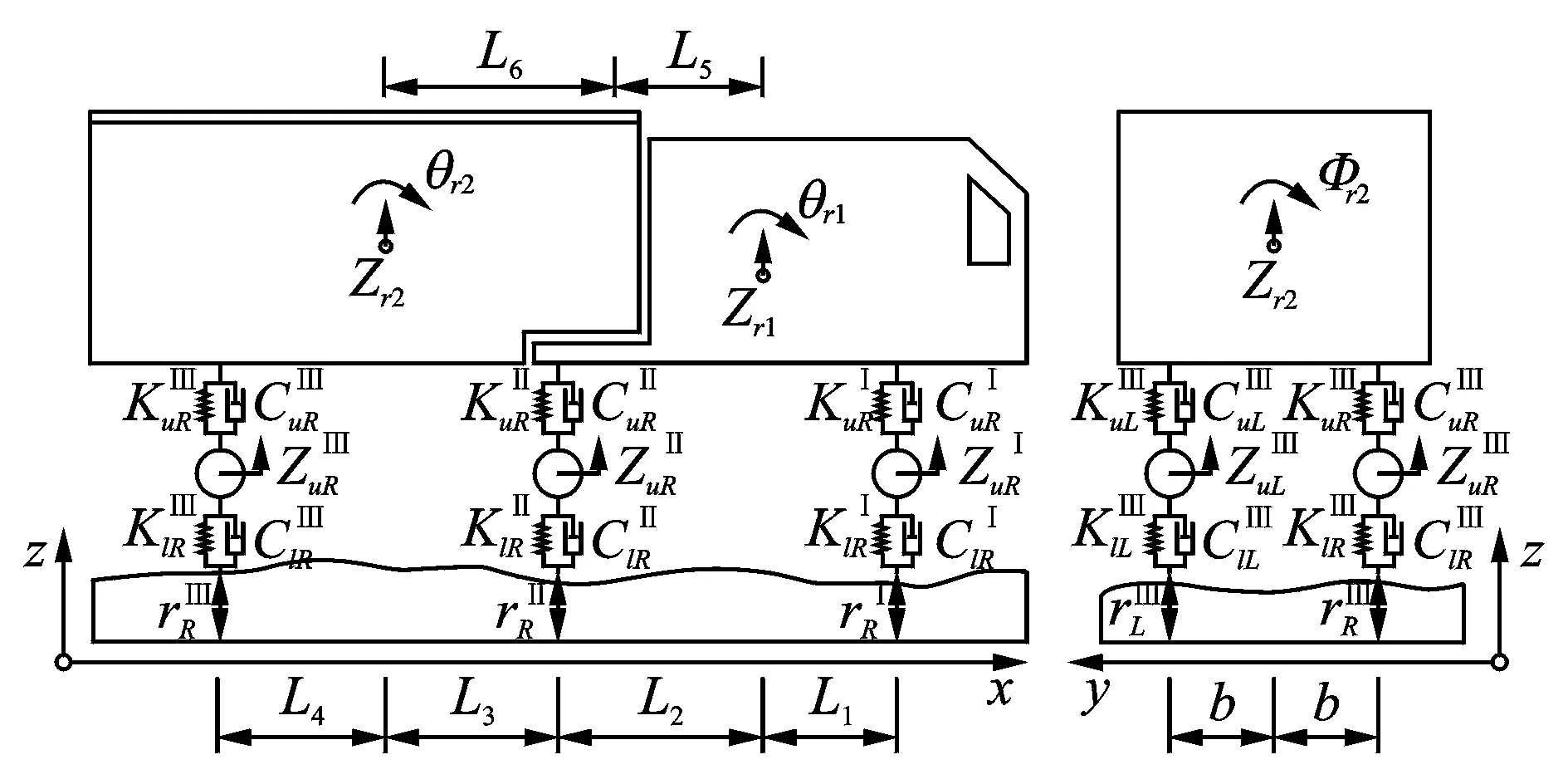
圖2 三軸車輛模型示意圖Fig.2 Schematic diagram of 3-axle vehicle model

3 路面平整度模擬

路面平整度是車橋耦合振動分析中的一個重要激勵源，而且具有較大的隨機性，對其進行數值模擬時，一般采用級數方法生成滿足功率譜函數的路面平整度曲線。其中路面平整度功率譜密度函數的計算公式為

(2)

式中φ(n0)為標準空間頻率對應的路面平整度系數，n與n0分別為空間頻率和標準空間頻率；n1和n2分別為路面功率譜在低頻段和高頻段的指數。

級數方法生成路面平整度曲線的公式為

(3)

式中x為沿橋軸方向的坐標；nk，Δn，N分別為空間頻率采樣點、采樣間距及采樣數；θk為在區間(0，2π)上的隨機相位角。

路面平整度按照國際標準化組織的劃分為5級：非常好(Very good)、好(Good)、中(Average)、差(Poor)和非常差(Very poor)[16]。本文選取其中的3種路面平整度，分別為好、中、差的路面情況(如圖3所示)進行分析。由于按照級數的方法生成的路面平整度曲線有較大隨機性，掩蓋了動力沖擊系數的本質規律，解決的辦法是采用多個路面平整度用于車橋耦合振動計算，從而獲取橋梁結構的多個動力響應值，然后求其平均值以減輕路面平整度隨機性的影響。

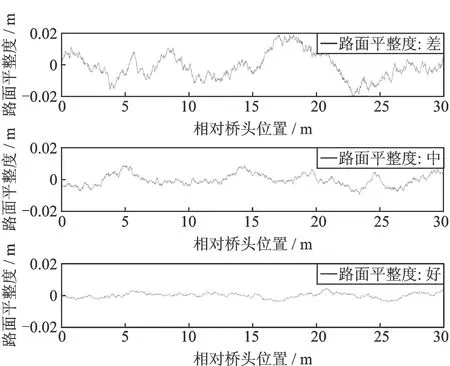
圖3 路面平整度曲線Fig.3 Curves of road roughness

4 車橋耦合方程的建立

為了建立移動車輛和波形鋼腹板PC箱梁橋兩者的動力耦合振動方程，首先分別建立了各自系統的動力方程，如下式所示：

(4)

(5)

式中M，C，K分別為質量、阻尼和剛度矩陣；d為系統位移向量；下標v和b分別代表車輛與橋梁；Fvg為車輛自重引起的等效結點荷載列向量；Fvr和Fbr為橋梁和車輛體系之間的相互作用力。

在橋面接觸點處車輛車輪和橋梁路面之間存在如下的位移關系：

(6)

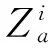
(7)

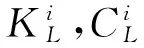
Fbr=Nbfbr

Fvr=Nvfvr

(8)

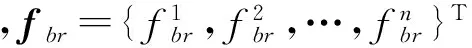
將式(6),(7)和(8)代入式(4)和(5)可得移動車輛與波形鋼腹板PC組合箱梁橋系統的耦合動力學方程，其表達式如下：

(9)

式中Cb-b，Cb-v，Cv-b,Kb-b,Kb-v，Kv-b，Fb-r，Fv-r是由車橋耦合效應產生的附加項。

直接積分法和模態綜合法是求解式(9)所示的時變運動方程的兩種主要方法[17]。本文采用模態綜合法，因為該方法對于結構較為復雜的橋梁可以減少計算工作量，并可獲得較為精確的數值解。在求解波形鋼腹板PC箱梁橋在車橋耦合振動作用下的動力響應時，首先采用ANSYS有限元軟件建立了波形鋼腹板PC箱梁橋的有限元模型，求得其自振頻率和振型，并提取模態矩陣為隨后計算橋梁的動力響應做準備，然后采用MATLAB軟件編制四階龍格庫塔方法并導入橋梁的模態矩陣求解方程(9)，從而獲得該橋型在車橋耦合振動作用下的動位移，最后結合式(1)求出波形鋼腹板PC箱梁橋的動力沖擊系數。

5 算 例

結合中國已建的鄄城黃河公路大橋與日本新開橋的設計實踐給出了單箱單室波形鋼腹板PC箱梁橋的橫截面尺寸(如圖4所示)和波形鋼腹板的幾何尺寸(如圖5所示)。橋梁的設計跨徑為30.9 m，計算跨徑為30.0 m，橋面為7.0 m+2×1.0 m= 9.0 m，兩車道行駛。沿橋梁縱向分別設置了2道端橫隔板和2道中橫隔板。橋梁主梁采用C50混凝土，彈性模量為3.5×104MPa，泊松比取值0.2，密度為2.5×103kg/m3。波形鋼腹板采用Q345C級鋼板彎折成型，厚度為9 mm，彈性模量為2.1×105MPa，泊松比取值0.3，密度為7.8×103kg/m3。

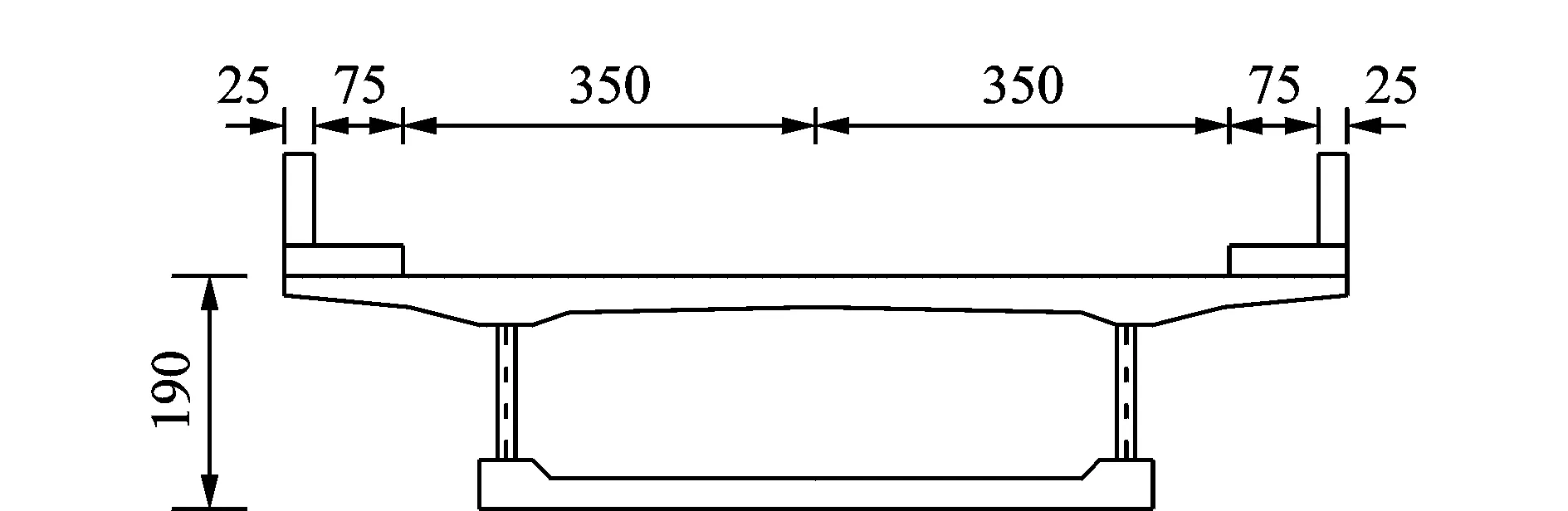
圖4 橫截面布置圖(單位：cm)Fig.4 Cross section of the bridge (Unit: cm)

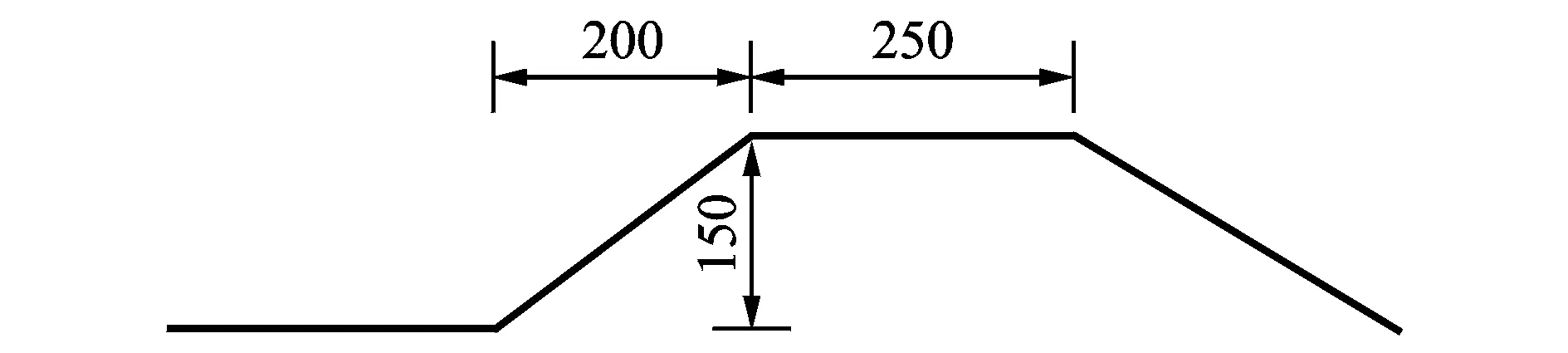
圖5 波形鋼腹板的幾何尺寸(單位：mm)Fig.5 Dimension of corrugated steel web (Unit: mm)

采用ANSYS 12.0建立了波形鋼腹板PC簡支箱梁橋的有限元模型。混凝土翼板和橫隔板使用實體單元SOLID45模擬；預應力筋采用LINK8桿單元模擬；波形鋼腹板采用殼單元SHELL63模擬，混凝土翼板和波形鋼腹板的連接采用嵌入式連接。建立完成的有限元模型如圖6所示。

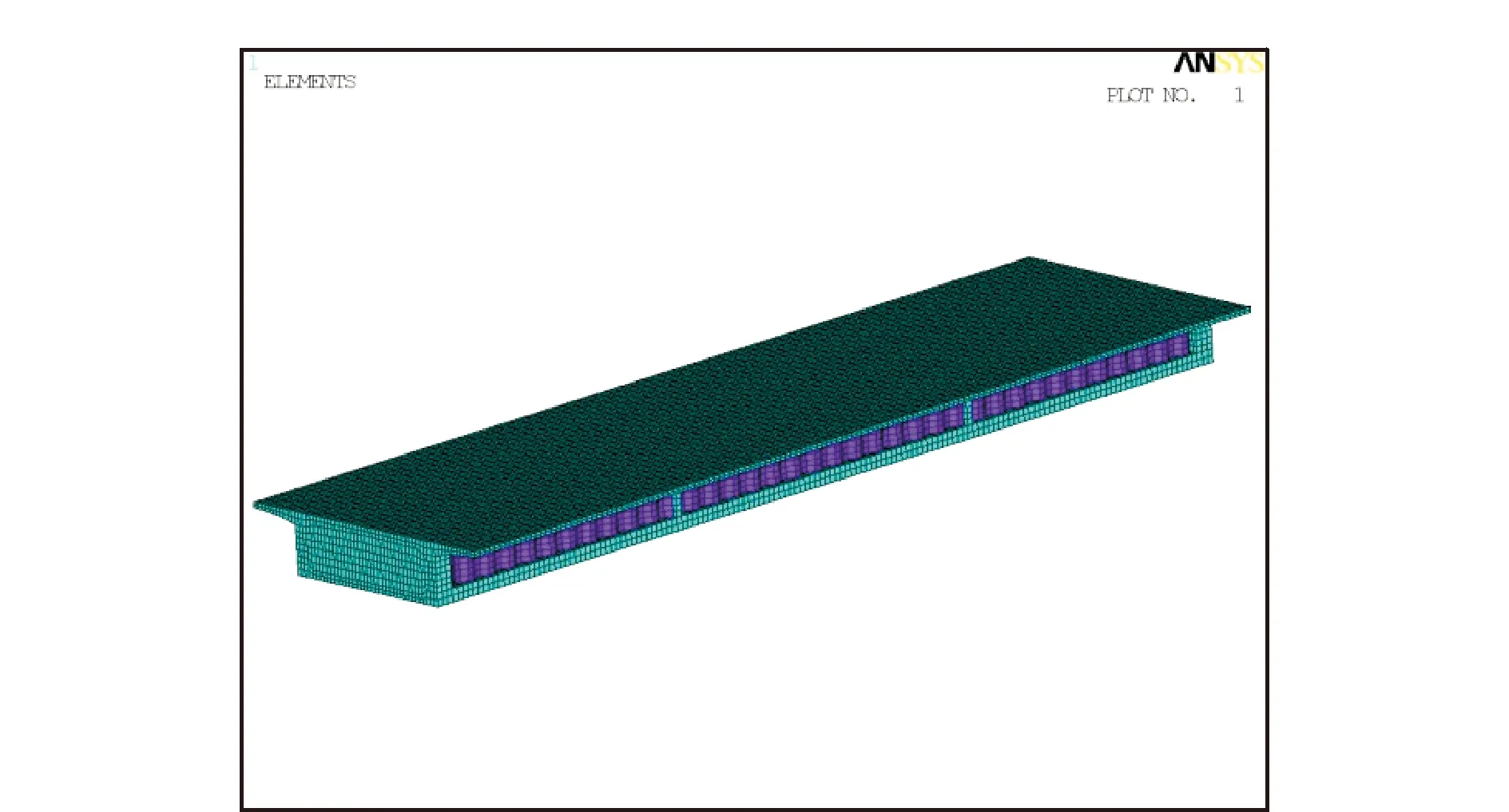
圖6 波形鋼腹板PC箱梁橋的有限元模型Fig.6 FEM of the PC box girder bridge with CSWs

6 動力方程的求解和沖擊系數計算

本文采用MATLAB軟件編制的車橋耦合計算程序可以計算不同車重、軸重、速度及路面平整度等情況下車橋耦合系統的振動響應。在文獻[14-15]已經驗證了計算程序的可靠性。采用該計算程序計算了表2所示的36種組合工況下波形鋼腹板PC箱梁橋的動力響應及相應跨中截面底板中心處撓度的動力沖擊系數。移動車輛沿行車道中心線行駛，加載位置如圖7所示。

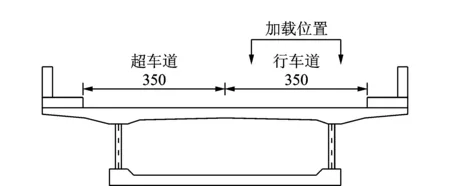
圖7 車輛行駛位置(單位：cm)Fig.7 Vehicle loading position (Unit: cm)

表2 動力沖擊系數計算工況

7 中國規范和相關文獻所得動力沖擊系數

中國現行規范中尚無單獨考慮波形鋼腹板PC箱梁橋沖擊系數的計算。《公路橋涵設計通用規范》JTG D60-2015和《城市橋梁設計規范》CJJ11-2011[18]中采用橋梁基頻計算橋梁動力沖擊系數。在JTG D60-2015規范和CJJ11-2011規范中，橋梁基頻的獲取方式有兩種：一是采用有限元方法計算橋梁的自振頻率(基頻)，二是利用常規橋梁結構基頻公式進行估算。在求得橋梁結構的基頻后，動力沖擊系數便可按下式進行確定

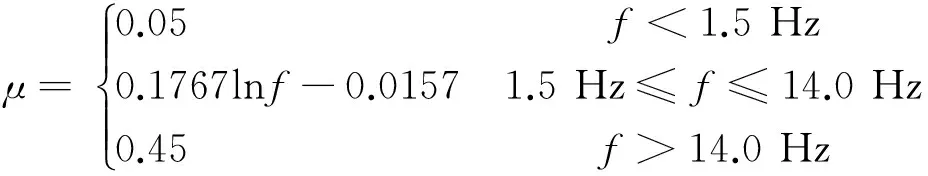
(10)

式中f為橋梁結構的基頻。

本文作者在文獻[12]中提出的一種求解波形鋼腹板PC簡支箱梁橋基頻的改進公式，如下式所示

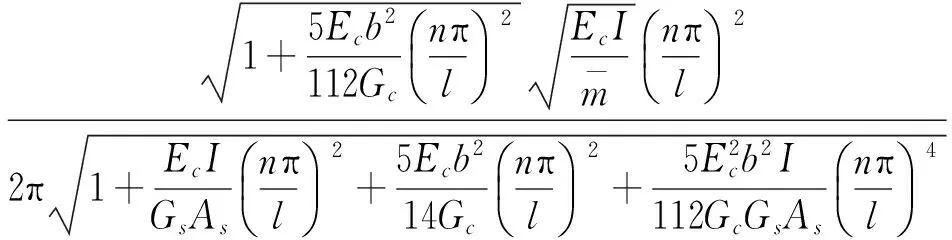
(11)

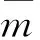
運用上述三種方法計算求得了波形鋼腹板PC簡支箱梁橋的基頻和動力沖擊系數，計算結果如表3所示。

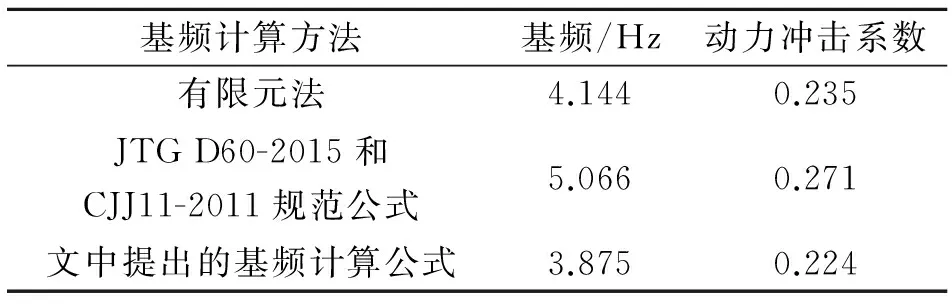
表3 不同方法所得動力沖擊系數

由表3可知，采用JTG D60-2015和CJJ11-2011規范中定義的估算公式計算所得的橋梁結構基頻與有限元方法求得的橋梁基頻具有較大的差異，從而導致兩種方法求出的動力沖擊系數也存在較大差異。運用作者提出的波形鋼腹板簡支箱梁橋基頻的計算公式求得的橋梁基頻則與有限元方法計算的基頻較為接近，兩種方法求得的動力沖擊系數也較為接近。考慮到有限元方法的巨大計算代價，以及規范基頻估算公式的較大差異，使用作者提出的波形鋼腹板簡支箱梁橋基頻的計算公式計算橋梁基頻以獲得橋梁結構的動力沖擊系數具有很好的參考價值。

8 結果分析

8.1 不同路面平整度下動力沖擊系數的均值與現行規范值對比

1#車和2#車在波形鋼腹板PC箱梁橋上行駛，每種車輛在不同路面平整度下分別有6種行駛速度，將1#車和2#車在不同路面平整度下的6種速度的動力沖擊系數求均值，并與規范所得的動力沖擊系數進行對比分析，對比結果如圖8所示。

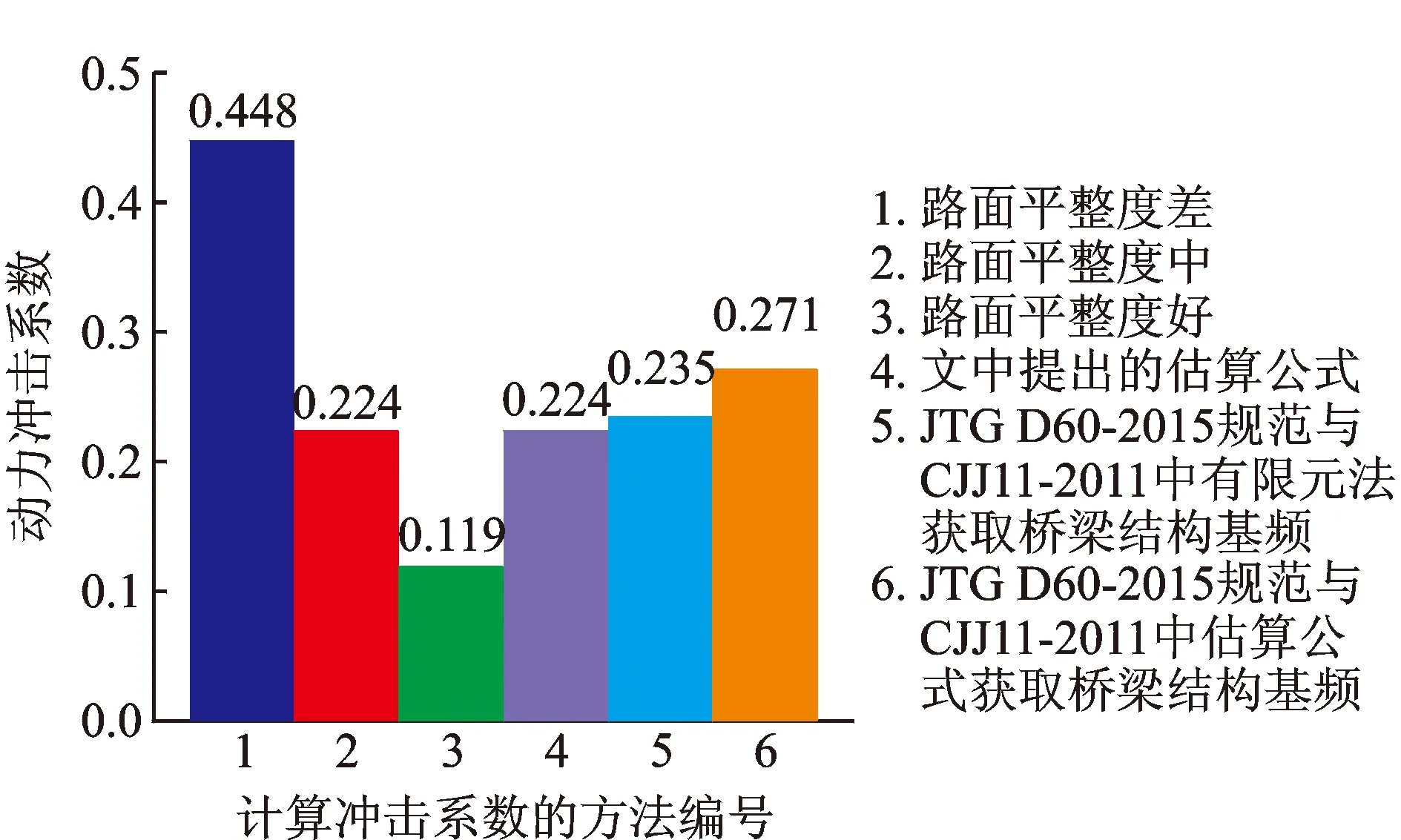
圖8 不同路面平整度及不同規范下波形鋼腹板PC箱梁橋的動力沖擊系數值對比Fig.8 Variation of mean IMs against different roughness and codes

由圖8可以看出，(1)路面平整度為好的情況下，動力沖擊系數的計算值小于JTG D60-2015和CJJ11-2011規范的設計值；(2)路面平整度為差的情況下，動力沖擊系數的計算值要比兩種規范設計值大很多；(3)路面平整度為中的情況下，動力沖擊系數的計算值與基于JTG D60-2015規范與CJJ11-2011規范中采用有限元法獲取基頻及文中提出的基頻計算公式獲取基頻后求得的動力沖擊系數吻合良好，而與基于JTG D60-2015規范與CJJ11-2011規范中采用估算公式獲取基頻后求得的動力沖擊系數有較大差異。

8.2 車速對動力沖擊系數的影響

圖9所示為路面平整度為好、中、差三種情況下兩種車型的動力沖擊系數隨車速的變化情況。

由圖9可知，對于1#車，當路面平整度為好和差時，動力沖擊系數的最大值出現在速度為15 m/s時；當路面平整度為中時，動力沖擊系數的最大值出現在速度為25 m/s時，而對于2#車，動力沖擊系數的最大值都出現在速度為10 m/s時，因此，車速對動力沖擊系數的影響較為復雜，無明顯規律。同時可以看出，1#車的基頻(1.926Hz)要比2#車的基頻(1.522Hz)更接近于橋梁結構的基頻，車輛基頻與橋梁結構基頻接近的話，越容易引發共振，引起的動力沖擊系數也就越大。

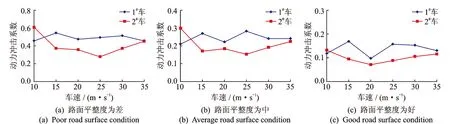
圖9 不同路面等級和車輛類型下的動力沖擊系數Fig.9 IMs variation with different roughness and vehicles

8.3 動力沖擊系數超規范工況數和超規范百分比統計

為了考察動力沖擊系數數值解與規范設計值差異的隨機性，定義動力沖擊系數數值解大于相應的規范設計值時的工況為超規范工況，定義超過規范相應工況的次數稱為超規范工況數；定義沖擊系數數值解超過規范設計值的百分比稱為超規范百分比。在不同路面平整度下，超規范工況數與超規范百分比的統計信息如表4所示，在表4中對比了兩類規范：JTG D60-2015規范與CJJ11-2011規范。

對于JTG D60-2015規范與CJJ11-2011規范而言：

(1)在路面平整度為好的情況下，未出現超規范工況。

(2)隨著路面狀況的惡化，超規范工況數和最大超規范百分比急劇增加。

表4 超規范工況數與最大超規范百分比

Tab.4 Statistic result of numbers of over-code-specified-value events and maximum relative variation

JTGD60-2015規范與CJJ11-2011規范1#車2#車路面平整度路面平整度好中差好中差超規范工況數046016超規范百分比-20%132%-27%158%

由表4還可以看出，總體的超規范工況數和相應的最大超規范百分比與車輛類型有關，1#車(重量較小，但基頻與本文研究的橋梁接近)，引起的超規范工況數要多于2#車(重量較大，但基頻與本文研究的橋梁相差要比1#車大)；但2#車要比1#車在路面平整度為中和差的情況下，引起的最大超規范百分比要大。因此，對于波形鋼腹板PC箱梁橋而言，車輛基頻與總體的超規范工況數有正相關關系，車重與引起的最大超規范百分比基本呈正相關關系。

9 結 論

本文建立了計算跨徑為30 m的單箱單室波形鋼腹板PC箱梁橋的有限元模型，對路面平整度、車型及車速等因素影響下的動力沖擊系數進行了計算，并考察了規范定義的動力沖擊系數的適用性；分析了路面平整度、車型、車速對動力沖擊系數的影響。通過本文的研究可以發現：

(1)移動車輛的基頻與波形鋼腹板PC箱梁橋的基頻接近的話，越容易引發共振，引起的沖擊系數就越大，二者呈正相關關系。動力沖擊系數不一定隨車重的增大而減小，與車型等其他因素也有一定關系。

(2)車輛行駛速度對動力沖擊系數的影響較為復雜，本文研究的兩種車型引起的動力沖擊系最大值分別對應著不同的行車速度。

(3)在路面平整度為中的情況下，波形鋼腹板PC簡支箱梁橋動力沖擊系數的計算值與JTG D60-2015規范及CJJ11-2011規范基于有限元法獲取基頻所求得的沖擊系數以及文中提出的基頻計算公式獲取基頻所得的沖擊系數吻合良好，因此建議在波形鋼腹板PC簡支箱梁橋設計時，采用JTG D60-2015規范與CJJ11-2011規范中基于有限元法獲取基頻和基于作者提出的基頻計算公式求其基頻，進而求得其動力沖擊系數。

(4)在路面平整度為優和差的情況下，波形鋼腹板PC簡支箱梁橋動力沖擊系數的數值解與規范值以及文中提出的基頻計算公式所得的沖擊系數值有較大差異。因此為科學合理地確定波形鋼腹板PC簡支箱梁橋的動力沖擊系數，宜采用車橋耦合振動理論分析所得的動力沖擊系數。

[1] 陳宜言. 波形鋼腹板預應力混凝土橋設計與施工[M]. 北京:人民交通出版社, 2009: 1—12.

Chen Yiyan. Composite Design and Construction of Composite Box Girder with Corrugated Steel Webs[M]. Beijing: China Communications Press, 2009: 1—12.

[2] NGUYEN N D, HAN S R, LEE G S, et al. Moment modification factor of I-girder with trapezoidal web corrugations considering concentrated load height effects[J]. Journal of Constructional Steel Research, 2011, 67(11): 1773—1787.

[3] NGUYEN N D, HAN S R, KIM J H, et al. Moment modification factors of I-girder with trapezoidal web corrugations under moment gradient[J]. Thin-Walled Structures, 2012, 57(8): 1—12.

[4] HASSANEIN M F, KHAROOB O F. Shear buckling behavior of tapered bridge girders with steel corrugated webs[J]. Engineering Structures, 2014, 74(9):157—169.

[5] K?VESDI B, JGER B, DUNAI L. Bending and shear interaction behavior of girders with trapezoidally corrugated webs[J]. Journal of Constructional Steel Research, 2016, 121(6): 383—397.

[6] 吳文清, 萬水, 葉見曙, 等. 波形鋼腹板組合箱梁剪力滯效應的空間有限元分析[J]. 土木工程學報, 2004, 37(9): 31—36.

WU Wenqing, WAN Shui, YE Jianshu, et a1. 3-D finite element analysis on shear lag effect in composite box girder with corrugated steel web [J]. China Civil Engineering Journal, 2004, 37(9): 31—36.

[7] 聶建國, 李法雄, 樊健生. 波形鋼腹板梁變形計算的有效剛度法[J]. 工程力學, 2012, 29(8): 71—79.

NIE Jianguo, LI Faxiong, FAN Jiansheng. Effective stiffness method for calculating deflection of corrugated web girder[J]. Engineering Mechanics, 2012, 29(8): 71—79.

[8] 李明鴻, 萬水, 蔣正文, 等. 波形鋼腹板混凝土組合梁撓度計算的初參數法[J]. 華南理工大學學報(自然科學版), 2015, 43(2): 66—74.

Li Minghong, Wan Shui, Jiang Zhengwen, et al. Initial parameter method for deflection calculation of concrete composite girder with corrugated steel webs[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(2): 66—74.

[9] Rui Juan Jiang, Francis Tat Kwong Au, Yu Feng Xiao. Prestressed concrete girder bridges with corrugated steel webs: review[J]. Journal of Structural Engineering, 2015, 141(2): 1—9.

[10]江克斌, 丁勇, 楊建奎, 等. 波形鋼腹板PC組合箱梁純扭作用下抗扭承載力試驗研究[J]. 工程力學, 2013, 30(6): 175—182.

JIANG Ke-bin, DING Yong, YANG Jian-kui, et a1. Experimental study on ultimate torsional strength of PC composite box-girder with corrugated steel webs under pure torsion[J]. Engineering Mechanics, 2013, 30(6): 175—182.

[11]JTG D60-2015, 公路橋涵設計通用規范[S].

JTG D60-2015, General Specifications for Design of Highway Bridge and Culverts[S].

[12]冀偉,劉世忠,藺鵬臻. 波形鋼腹板組合箱梁振動頻率分析與試驗[J]. 中國公路學報, 2013, 26(5): 102—107.

JI Wei, LIN Shizhong, LIN Pengzhen. Study on influencing factors of vertical frequency of the box girder with corrugated steel webs[J]. China Journal of Highway and Transport, 2013, 26(5): 102—107.

[13]陳志興. 波形鋼腹板箱梁橋車橋耦合振動沖擊系數研究[J].山西建筑, 2014, 40(13): 176—178.

CHEN Zhixing. Study on impact coefficient of coupling vibration of vehicle bridge girder bridge with corrugated steel web box[J]. Shanxi Architecture, 2014, 40(13): 176—178.

[14]Deng L, Cai C S. Identification of parameters of vehicles moving on bridges[J]. Engineering Structures, 2009, 31(10):2474—2485.

[15]Deng L, Cai C S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges[J]. Engineering Structures, 2010, 32(1): 21—31.

[16]International Organization for Standard (ISO). Mechanical vibration-road surface profiles-reporting of measured data. ISO 8068: 1995(S). ISO[S]. Geneva, 1995.

[17]李小珍, 張黎明, 張潔. 公路橋梁與車輛耦合振動研究現狀與發展趨勢[J]. 工程力學, 2008, (03): 230—240.

LI Xiao-zhen, ZHANG Li-ming, ZHANG Jie. State-of-the-art review and trend of studies on coupling vibration for vehicle and highway bridge system[J]. Engineering Mechanics. 2008, (03): 230—240.

[18]CJJ11-2011, 城市橋梁設計規范[S].

CJJ11-2011, Code for Design of the Municipal Bridge[S].

Vehicle-bridge coupled vibration analysis and calculation of dynamic impact
factor for the PC box-girder bridge with corrugated steel webs

JIWei1,DENGLu2,HEWei2

(1.College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;
2.College of Civil Engineering, Hunan University, Changsha 410082, China)

As a new type of steel-concrete composite structure, the pre-stressed concrete (PC) box-girder bridges with corrugated steel webs(CSWs)have been widely used in bridge engineering all over the world because of their excellent mechanical performance and light weight. Research on the dynamic response and dynamic impact factor (IM) of this new structure are limited, and no standard file has yet been established. In order to determine the IMs of the simple supported PC box-girder bridges with CSWs scientifically and reasonably, the two systems of motion equations for the vehicle and bridge are coupled through the contact condition between the vehicle wheels with bridge deck. Considered the random excitation effects of road surface profile, the vibration responses of the bridge nodes can be obtained by using the MATLAB program to solve the dynamic equation of vehicle-bridge system and the IMs of simple supported PC box girder-bridge with CSWs can be obtained. The obtained numerical IMs are compared to IMs obtained from the General Specifications for Design of Highway Bridge and Culverts JTG D60-2015 and IMs based on the formula of fundamental frequency proposed by the author. The results show that under the average road surface conditions, the IMs calculated using the proposed formula of fundamental frequency are in good agreement with IMs based on the fundamental frequency calculated by the finite element method suggested by the JTG D60-2015 and the IMs from numerical simulations, while have significant differences with the IMs calculated using estimation formula of the fundamental frequency suggested by the JTG D60-2015. The conclusions can provide a good reference for dynamic response analysis and determining the dynamic impact factors of PC box-girder bridges with CSWs.

vehicle-bridge interaction; corrugated steel web; composite box girder; vibration frequency; dynamic impact factor

2015-09-14；

2016-06-22

國家自然科學基金資助項目(51368032)；中國博士后科學基金資助項目(2014M562103)；甘肅省高等學校科研項目(2015A-053)；甘肅省基礎研究創新群體項目資助(1506RJIA029)；蘭州交通大學優秀平臺資助項目(201601)

U441+.3

1004-4523(2016)06-1041-07

10.16385/j.cnki.issn.1004-4523.2016.06.013

冀偉(1982—),男，博士,副教授。電話:13919891668;E-mail:jiwei1668@163.com