命題知識與自學能力的培養一探
陳團義
(廈門海滄實驗中學)
命題知識與自學能力的培養一探
陳團義
(廈門海滄實驗中學)
為適應社會發展,培養學生如何獨立獲取知識已成為當前教育界的共識。初中生要能比較順利地自學數學至少應具備如下三個方面的素質:首先對某一數學命題的真假性要能做出正確判斷;其次要有一定的分析與綜合能力;最后要會把頭腦里想的問題正確地寫出來。學好初中教材中的命題知識能為學生具備以上三個方面的素質奠定良好基礎,應引起重視。
命題知識;自學能力;解題思路
一、深刻領會命題的結構,加強對基礎知識的理解
學生在自學初中數學教材內容的過程中遇到代數、幾何、統計與概率中的很多定義、法則、性質、公式、定理、公理等,它們多以命題的形式出現。比如:
1.定義
(1)如果一個數的平方等于a,那么這個數就叫做a的平方根。
(2)兩組對邊分別平行的四邊形叫做平行四邊形。
(3)眾數是一組數據中出現次數最多的那個數據值。
2.法則
兩數相乘,同號得正,異號得負,并把絕對值相乘。
3.性質
平行四邊形的兩組對邊分別相等。
4.公式
兩數和與兩數差的積,等于這兩個數的平方差。
5.定理
如果兩條直線都和第三條直線平行,那么這兩條直線也互相平行。
6.公理
兩點之間線段最短。
從以上例題可以看出初中數學知識點多以命題的形式出現,因而它們都具備命題的結構特征,即:都由題設和結論兩部分組成,題設是命題的已知項,結論是由已知項推出的項。明白這一點有助于學生在自學過程中理解所學的基礎知識。
二、學會證明假命題培養思維批判性
學生在自學過程中思維需要有一定的批判性,他們在解決問題的過程中要對每一步推理的合理性做出正確的判斷,只有這樣才能決定這一思維是否繼續下去,直至問題解決。
例1.判斷下列各題,結論正確的在括號內打√,錯誤的打×。
①三角形的一個外角大于三角形的任何一個內角。( )
②如果兩個三角形的三個內角分別相等,那么這兩個三角形全等。 ( )
③若a>b,則a+2c>b+2c。 ( )
第①題可舉反例:如圖1,∠1是三角形的一個外角,∠2是三角形的一個內角,但∠1<∠2,所以它是假命題,應打×。
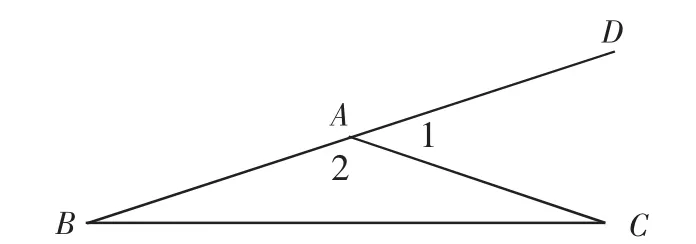
圖1
第②題可舉反例:如圖2,△AEF和△BGH都是等邊三角形,顯然它們的三個內角都相等,但它們不全等,所以它是假命題,應打×。

圖2
第③題是真命題,它符合不等式的基本性質,應打√。
三、類比真命題培養學生的發散思維
學生在自學過程中利用命題知識將具有相同題設不同結論和相同結論不同題設的知識點(定義、定理或公理)進行分類總結,對優化知識結構,發展思維能力,形成一定的分析綜合能力,提高自學水平是很有幫助的,其實,這也就是發散性思維。
例2.下列命題哪些題設相同,哪些結論相同。
①同位角相等,兩直線平行。
②內錯角相等,兩直線平行。
③同旁內角相等,兩直線平行。
④同平行第三條直線的兩直線平行。
⑤平行四邊形的對邊平行。
教學中重視對相同題設不同結論的命題進行概括,可提高學生對題目已知條件的分析能力,快速找到解題思路;對相同結論不同題設的命題進行概括可提高學生對結論的分析能力,尋找不同的解題思路。
四、懂得真命題與數學書寫的關系
學生在自學數學過程中會接觸到數學語言,比如,在自學平面幾何時就涉及三種語言:一是文字語言,二是符號語言,三是圖形語言。這三者緊密聯系,部分初學者通常不能很好地理解,導致學習難度增加,重視命題知識的教學可以很好地解決這一問題。
例3.定理“如果兩條直線都和第三條直線平行,那么這兩條直線也互相平行”是文字語言。
結合圖形語言:

它所對應的符號語言是“∵AB∥EF,CD∥EF ∴AB∥CD”
從上面可以看出:一條定理(或公理)對應一步推理,學生的推理能力也是由學會一步推理到兩步推理到三步推理這樣慢慢發展起來的,教學過程中應讓學生明白這一點,才能理解幾何的證明書寫形式,降低自學過程中的難度,對提高幾何的自學能力是很有幫助的。
總之,重視命題知識的教學,能幫助學生更好地理解基礎知識,形成一定的分析綜合能力,培養良好的思維品質,學會正確地用數學語言表達,為學生自學能力的培養奠定良好的基礎。
施若谷.科學技術史新編[M].廈門大學出版社,1998.
·編輯 王團蘭

