系統(tǒng)辨識(shí)中應(yīng)用遺傳算法的分析及研究*
佘明洪
(1.重慶電子工程職業(yè)學(xué)院,重慶 401331;2.重慶大學(xué)自動(dòng)化學(xué)院,重慶 400044)
系統(tǒng)辨識(shí)中應(yīng)用遺傳算法的分析及研究*
佘明洪1,2
(1.重慶電子工程職業(yè)學(xué)院,重慶 401331;2.重慶大學(xué)自動(dòng)化學(xué)院,重慶 400044)
文章首先闡述了系統(tǒng)辨識(shí)與遺傳算法,隨后對(duì)遺傳算法在系統(tǒng)辨識(shí)中的具體應(yīng)用進(jìn)行論述。期望通過(guò)文章的研究能夠?qū)Υ龠M(jìn)遺傳算法在系統(tǒng)辨識(shí)中的推廣應(yīng)用有所幫助。
系統(tǒng)辨識(shí);遺傳算法;應(yīng)用
1 系統(tǒng)辨識(shí)與遺傳算法概述
1.1 系統(tǒng)辨識(shí)
系統(tǒng)辨識(shí)是指以輸入和輸出數(shù)據(jù)為基礎(chǔ),從某一類模型當(dāng)中確定出一個(gè)與被測(cè)系統(tǒng)等價(jià)的模型。該定義中的關(guān)鍵要素有三個(gè),即數(shù)據(jù)、模型和等價(jià)準(zhǔn)則。可將系統(tǒng)辨識(shí)分為整體辨識(shí)和部分辨識(shí)。
1.2 遺傳算法
遺傳算法簡(jiǎn)稱GA,是一種計(jì)算模型,能夠通過(guò)模擬自然進(jìn)化過(guò)程獲取最優(yōu)解。適應(yīng)度是該方法最基本的搜索信息,不需要其它的輔助信息,由此使得GA成為智能計(jì)算的關(guān)鍵技術(shù)之一。GA具備全局性、高效性、并行性、魯棒性、易擴(kuò)展性、普適性、簡(jiǎn)明性等優(yōu)點(diǎn)。
2 遺傳算法在系統(tǒng)辨識(shí)中的具體應(yīng)用
系統(tǒng)辨識(shí)的對(duì)象包括系統(tǒng)參數(shù)和系統(tǒng)結(jié)構(gòu)。傳統(tǒng)辨識(shí)方法僅能辨識(shí)其中一種,而GA可以辨識(shí)兩種。
2.1 GA在系統(tǒng)參數(shù)辨識(shí)中的應(yīng)用
運(yùn)用GA對(duì)系統(tǒng)參數(shù)進(jìn)行辨識(shí)的過(guò)程中,需要先建立一個(gè)模型,借助該模型將參數(shù)辨識(shí)問(wèn)題轉(zhuǎn)化為GA對(duì)模型參數(shù)的優(yōu)化問(wèn)題。利用二進(jìn)制對(duì)各個(gè)參數(shù)進(jìn)行編碼處理,使其構(gòu)成子串,隨后以拼接的方式將子串構(gòu)成“染色體”串。便于分析研究,可將系統(tǒng)描述成如下形式:

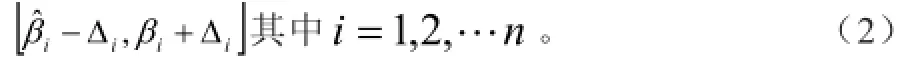

(3)確定適應(yīng)度函數(shù)。估計(jì)的函數(shù)模型應(yīng)當(dāng)與實(shí)際數(shù)值的誤差越小越好,而GA規(guī)定適應(yīng)度函數(shù)的值越大,則表明該“染色體”的優(yōu)越性越強(qiáng)。設(shè)該模型與已知實(shí)際值的誤差平方和的倒數(shù)為最優(yōu)模型估計(jì)的標(biāo)準(zhǔn),由此可得適應(yīng)度函數(shù)為經(jīng)過(guò)計(jì)算,生成的“染色體”分別對(duì)應(yīng)十進(jìn)制值,隨后從中找到使適應(yīng)度達(dá)到最大的“染色體”,與之相對(duì)應(yīng)的十進(jìn)制數(shù)即為本次計(jì)算所得的最優(yōu)解。最后采用多次循環(huán)的方法,便可獲得最優(yōu)模型。通過(guò)誤差驗(yàn)證,遺傳算法在系統(tǒng)參數(shù)辨識(shí)中具有較高的精確性。
2.2 GA在系統(tǒng)結(jié)構(gòu)辨識(shí)中的應(yīng)用
GA是一種模擬生物進(jìn)化現(xiàn)象的優(yōu)化方法,將定向與隨機(jī)搜索有機(jī)結(jié)合,通過(guò)潛在解的群體實(shí)現(xiàn)全局尋找最優(yōu)解的目標(biāo)。GP是GA的擴(kuò)展與延伸,它使用變長(zhǎng)層次結(jié)構(gòu)的程序樹(shù),克服了GA定長(zhǎng)編碼的局限性,有利于復(fù)雜問(wèn)題的表述。GP在運(yùn)算速度上也要優(yōu)于GA。由于系統(tǒng)結(jié)構(gòu)辨識(shí)是一個(gè)較為復(fù)雜的問(wèn)題,因此可運(yùn)用GP來(lái)解決此類問(wèn)題,具體方法如下:
(1)生成初始個(gè)體。GP中的所有個(gè)體全部都是由算法樹(shù)刻畫(huà)的函數(shù)表達(dá)式,為便于動(dòng)態(tài)修改,可將算法樹(shù)視作為GP的對(duì)象。在初始個(gè)體生成的過(guò)程中,從F(函數(shù)集)中以均分、隨機(jī)的方法選一個(gè)函數(shù)作為根節(jié)點(diǎn),主要目的是為了生成具有層次化特點(diǎn)的復(fù)雜結(jié)構(gòu)。當(dāng)根節(jié)點(diǎn)選好之后,可以按照發(fā)出的線數(shù),從F與終止符的并集當(dāng)中,選出一個(gè)尾節(jié)點(diǎn),此時(shí)算法樹(shù)生成過(guò)程終止。
(2)生成初始群體。在GP中,初始群體的產(chǎn)生有兩種方法,一種是生長(zhǎng)法,深度優(yōu)先;另一種是完全法,寬度優(yōu)先。為使群體的形態(tài)更加豐富,搜索點(diǎn)能夠最大限度地分布,可將兩種方法結(jié)合,以此來(lái)生成初始群體。
(3)算子。在GP中的基本算子主要包括復(fù)制、交換與突變。復(fù)制是將上一代的優(yōu)良個(gè)體帶入到下一代群體當(dāng)中,遵循優(yōu)勝劣汰的原則;交換則是整個(gè)子樹(shù)的交換,為避免交換過(guò)程中產(chǎn)生出巨形個(gè)體,必須使用樹(shù)的最大允許深度對(duì)交換過(guò)程進(jìn)行控制;在GP中,突變的作用較小,每一代個(gè)體中僅有5%左右會(huì)發(fā)生突變。
(4)辨識(shí)步驟。先確定出個(gè)體的表達(dá)方式,生成初始群體,執(zhí)行相關(guān)的遺傳操作,如復(fù)制、交換等,循環(huán)執(zhí)行,直至達(dá)到終止條件。
3 結(jié)束語(yǔ)
綜上所述,遺傳算法在系統(tǒng)參數(shù)辨識(shí)中具有較高的精確性,并能對(duì)復(fù)雜的非線性系統(tǒng)結(jié)構(gòu)進(jìn)行辨識(shí),其克服了傳統(tǒng)辨識(shí)方法的不足,具有一定的推廣使用價(jià)值。
[1]劉正龍,楊艷梅,羅玉軍.基于遺傳算法的非線性系統(tǒng)辨識(shí)的研究[J].黑龍江大學(xué)自然科學(xué)學(xué)報(bào),2014,(6):76-78.
[2]趙林,魏彤.基于“自適應(yīng)遺傳算法”的磁軸承系統(tǒng)辨識(shí)[J].自動(dòng)化與儀表,2014,(4):55-57.
[3]任燕燕.基于智能計(jì)算的非線性系統(tǒng)辨識(shí)算法研究及其應(yīng)用[D].華北電力大學(xué).2014.
TP301.6
A
2096-2789(2016)12-0011-01
重慶市高等教育教學(xué)改革研究重點(diǎn)項(xiàng)目,高職院校電子信息類專業(yè)實(shí)踐教學(xué)評(píng)價(jià)體系的研究與構(gòu)建(項(xiàng)目編號(hào):142059)。

