數(shù)學(xué)建模應(yīng)用于土木工程土方調(diào)配芻議
劉 軍
(安徽理工大學(xué)土木建筑學(xué)院,安徽 淮南 232001)
數(shù)學(xué)建模應(yīng)用于土木工程土方調(diào)配芻議
劉 軍
(安徽理工大學(xué)土木建筑學(xué)院,安徽 淮南 232001)
大型土方工程施工中,可利用運(yùn)籌學(xué)當(dāng)中的線性規(guī)劃知識(shí),構(gòu)建數(shù)學(xué)模型,通過(guò)進(jìn)行多次運(yùn)算步驟操作之后,最終確定運(yùn)距最短的土方調(diào)配相應(yīng)最優(yōu)方案。并作為施工指導(dǎo),以此實(shí)現(xiàn)成本降低,獲取更好經(jīng)濟(jì)效益。
數(shù)學(xué)建模;土方調(diào)配;線性規(guī)劃
在土木建筑工程大型化的土方施工過(guò)程中,為實(shí)現(xiàn)工程造價(jià)及成本降低,通常需在施工開展前,制定完備的土方調(diào)配方案,以此為施工提供指導(dǎo)。而在現(xiàn)實(shí)施工中,諸多工程施工人員在方案制定時(shí),僅憑借自身一些經(jīng)驗(yàn)和嘗試進(jìn)行抉擇。當(dāng)然,憑借以往經(jīng)驗(yàn)優(yōu)勢(shì)確實(shí)可以獲取較為滿意的方案,但如若問題比較復(fù)雜,僅僅憑借自身常識(shí)與經(jīng)驗(yàn),則會(huì)存有較大困難。而通過(guò)運(yùn)籌學(xué)當(dāng)中有關(guān)線性規(guī)劃方面的知識(shí),便能夠以一種較為簡(jiǎn)單的方式,獲取目標(biāo)明確的最佳方案。文章以實(shí)際案例方式,構(gòu)建數(shù)學(xué)模型,運(yùn)用線性規(guī)劃知識(shí),對(duì)土方調(diào)配相應(yīng)最佳方案的求解方法予以給出,即表上作業(yè)法。
1 構(gòu)建數(shù)學(xué)模型
1.1 編制土方調(diào)配表
土方調(diào)配表見表1,表格當(dāng)中的 表示待求的土方調(diào)運(yùn)量,從第 個(gè)挖方區(qū)向第 個(gè)填方區(qū)調(diào)運(yùn)的土方量。如 乃是 挖方區(qū)向 填方區(qū)調(diào)運(yùn)的土方量,表格內(nèi)最右邊的數(shù)值,乃是調(diào)配區(qū)所具有的實(shí)際運(yùn)距。
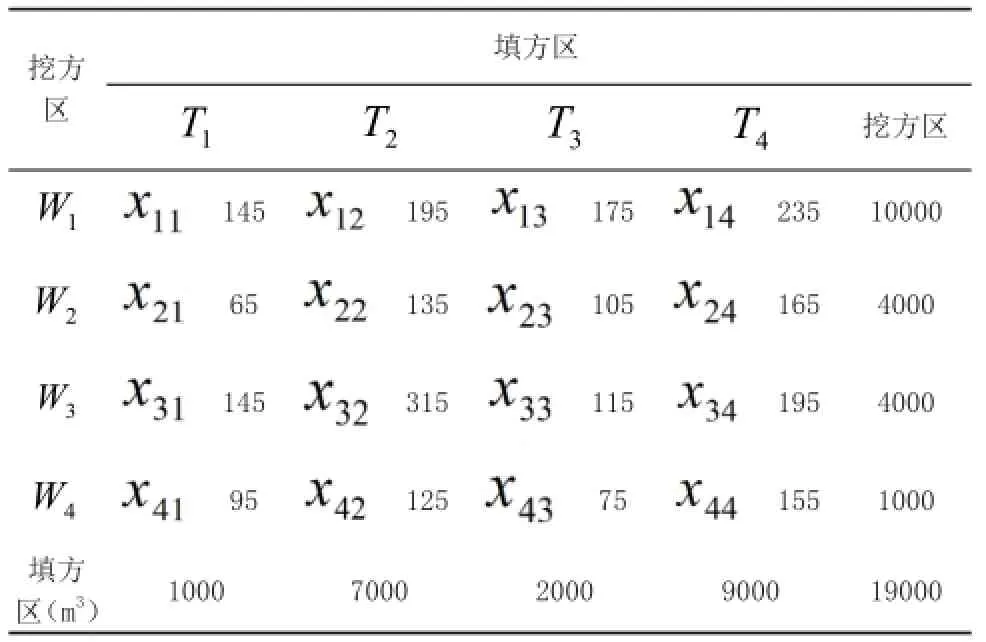
表1 土方調(diào)配表
1.2 構(gòu)建數(shù)學(xué)模型
目標(biāo)函數(shù):

由所構(gòu)建的數(shù)學(xué)可行得知,此問題實(shí)際上是一個(gè)有關(guān)線性規(guī)劃的問題。可采用單純形法進(jìn)行求解,但是運(yùn)用此方法實(shí)施求解,則需針對(duì)各約束方程,外加一個(gè)對(duì)應(yīng)的人工變量,最終構(gòu)成求解4+4個(gè)約束,一共包括有4×4+4+4各變量的問題。此種解題思路,具有十分大的工作量。通過(guò)觀察模型得知,此模型具有一定特殊性,全部4個(gè)約束方程,均僅為各個(gè)變量的綜合。也就是在約束方程當(dāng)中的各個(gè)變量所存有的對(duì)應(yīng)系數(shù),不“1”則為“0”,因此,在這里可不將人工變量引入其中,而運(yùn)用一種同樣特殊的表上作業(yè)法,實(shí)施求解操作。
2 初始調(diào)配方案編制
制定初始方案中,選用有限具有最小運(yùn)距的調(diào)配區(qū)實(shí)施調(diào)配。基于此原則,可促使目標(biāo)函數(shù)在具體的運(yùn)算次數(shù)方面的減少。①通過(guò)上述表1可知,未知量具有最小的運(yùn)距,因從當(dāng)中調(diào)運(yùn)1000m3至也就是=1000m3,因已經(jīng)得到相應(yīng)足土方,故和則不同給予土方,即可得到與之對(duì)應(yīng)的方格當(dāng)中則可填寫成0;②然后再選擇一個(gè)最小運(yùn)距的方格實(shí)施調(diào)配操作,在沒有進(jìn)行調(diào)配的方格當(dāng)中,最小的運(yùn)距則為由此便可得出,=1000m3,即=0;③對(duì)上述步驟進(jìn)行重復(fù)操作,每次均對(duì)最小運(yùn)距的方格實(shí)施相應(yīng)調(diào)配操作。依據(jù)具體的供需需求,對(duì)此方格相應(yīng)需求盡可能給予滿足,且依次將其它求出,也就可將初始調(diào)配方案得出。
3 調(diào)配方案最優(yōu)化檢驗(yàn)
依據(jù)對(duì)最小運(yùn)距進(jìn)行優(yōu)先選擇的原則,因此,所獲取的最小目標(biāo)函數(shù)值,不能保證其是最小的,所以需對(duì)其實(shí)施檢驗(yàn)。制定一個(gè)假想運(yùn)距,假想運(yùn)距乃是整個(gè)假定方案當(dāng)中最優(yōu)時(shí)候的虛擬運(yùn)距。在相應(yīng)假想運(yùn)距條件下,任意調(diào)整方案,但是其目標(biāo)函數(shù)值S不發(fā)生改變。所以當(dāng)原運(yùn)距都等于或者大于與之處于對(duì)應(yīng)狀態(tài)的假想運(yùn)距時(shí),則此時(shí)的目標(biāo)函數(shù)值,便不能再次降低,所以此方案乃為最優(yōu)。相反,當(dāng)目標(biāo)函數(shù)值仍然能夠再次降低時(shí),則方案并不是最優(yōu)。
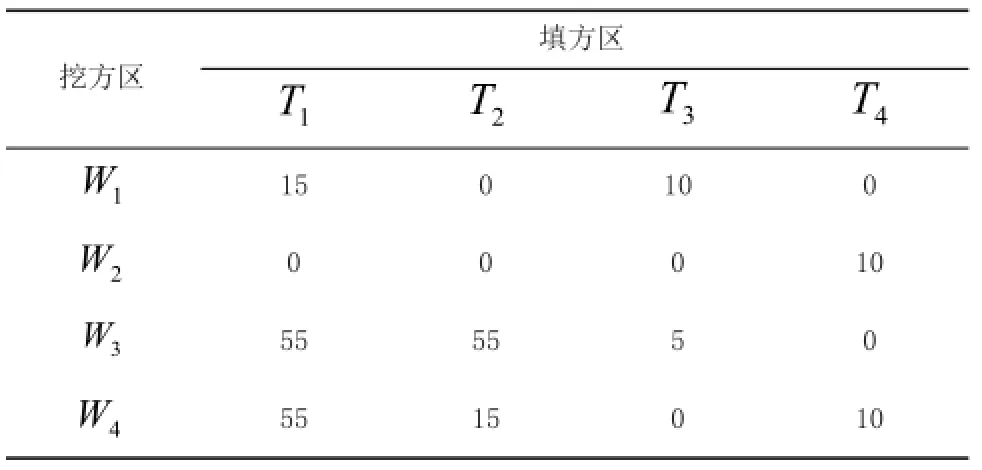
表2 檢驗(yàn)表
4 繪制土方調(diào)配圖
根據(jù)最優(yōu)方案原則實(shí)施繪制,即可得到土方調(diào)配圖(見圖1),以此對(duì)現(xiàn)場(chǎng)施工進(jìn)行指導(dǎo)。
U416.1+11
A
2096-2789(2016)12-0232-02

