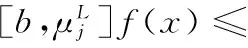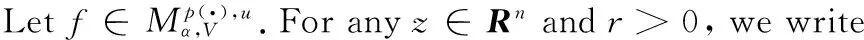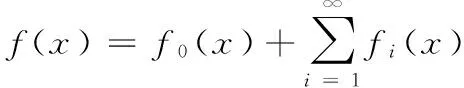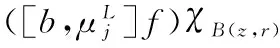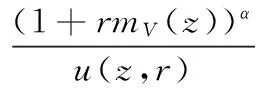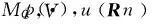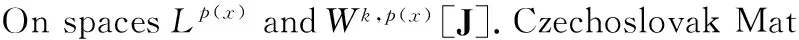Commutator of Marcinkiewicz Integrals Associated with Schr?dinger Operators on Variable Exponent Spaces
SHU Yu
(Department of Economic and Trade, Anhui Business College Vocational Technology, Wuhu 241002, China)
Commutator of Marcinkiewicz Integrals Associated with Schr?dinger Operators on Variable Exponent Spaces
SHU Yu
(Department of Economic and Trade, Anhui Business College Vocational Technology, Wuhu 241002, China)
In this paper, we prove the boundedness of commutator of Marcinkiewicz integrals associated with Schr?dinger operators on variable exponent spaces.
Marcinkiewicz integrals; commutator; Schr?dinger operator; variable exponent; Morrey spaces
Classification code:O174.3 Document code: A Paper No:1001-2443(2016)06-0535-07
0 Introduction
In this paper, we consider the Schr?dinger differential operator onRn(n≥3).
L=-△+V(x)
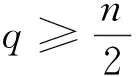
AnonnegativelocallyLqintegrablefunctionV(x)onRnis said to belong toBq(q>1)ifthereexistsaconstantC>0suchthatthereverseH?lderinequality
holdsforeveryballinRn, see [1].
The commutator of Marcinkiewicz integral operatorμbisdefinedby
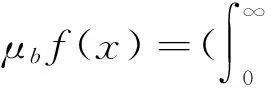
Stein[2]firstintroducedtheoperatorμandprovedthatμisoftype(p,p)(1 It is well known that function spaces with variable exponents were intensively studied during the past 20 years, due to their applications to PDE with non-standard growth conditions and so on, we mention e.g. ([8, 9]). A great deal of work has been done to extend the theory of maximal, potential, singular and Marcinkiewicz integrals operators on the classical spaces to the variable exponent case, see([10]-[15]). It will be an interesting problem whether we can establish the boundedness of commutator of Marcinkiewicz integrals associated with Schr?dinger operators on variable exponent spaces. The main purpose of this paper is to answer the above problem. To meet the requirements in the following sections, here, the basic elements of the theory of the Lebesgue spaces with variable exponent are briefly presented. Letp(·):Rn→[1,∞) be a measurable function. The variable exponent Lebesgue spaceLp(·)(Rn) is defined by Lp(·)(Rn)isaBanachspacewiththenormdefinedby Wedenote LetP(Rn)bethesetofmeasurablefunctionp(·)onRnwith value in [1,∞) such that 1 andonedefines B(Rn)isthesetofp(·)∈P(Rn)satisfyingtheconditionthatMisboundedonLp(·)(Rn). Forx∈Rn,thefunctionmV(x)isdefinedby Forbrevity,inthispaper,Calwaysmeansapositiveconstantindependentofthemainparametersandmaychangefromoneoccurrencetoanother.B(x,r)={y∈Rn:|x-y| Definition 1.1[12]For anyp(·)∈B(Rn),letkp(·)denotethesupremumofthoseq>1suchthatp(·)/q∈B(Rn).Letep(·)betheconjugateofkp′(·). Definition 1.2[12]Letp(·)∈L∞(Rn)and1 (1) WedenotetheclassofMorreyweightfunctionsbyWp(·). NextwedefinetheMorreyspaceswithvariableexponentrelatedtothenonnegativepotentialV. Nowitisinthispositiontostateourresults. Theorem 1.1 SupposeV∈Bqwithq>1andp(x)∈B(Rn),then Theorem 1.2 SupposeV∈Bqwithq>1,b∈BMO,-∞<α<∞andp(x)∈B(Rn).If (2) then Remark 1 We can easily show thatufulfills(2)impliesu∈Wp(·),see[16]. Inordertoproveourresult,weneedsomeconclusionsasfollows. Lemma 1.1[18]Letp(·)∈P(Rn):Thenthefollowingconditionsareequivalent: (1)p(·)∈B(Rn). (2)p′(·)∈B(Rn). (3) (p(·)/q∈B(Rn)forsome1 (4) (p(·)/q)′∈B(Rn)forsome1 Lemma1.1ensuresthatkp(·)iswell-definedandsatisfies1 Lemma 1.2[19]Ifp(·)∈P(Rn),thenforallf∈Lp(·)(Rn)andallg∈Lp′(·)(Rn)wehave ∫Rn|f(x)g(x)|dx≤rp‖f‖Lp(·)(Rn)‖g‖Lp′(·)(Rn), whererp:=1+1/p--1/p+. Lemma 1.3[10]Ifp(·)∈B(Rn),thenthereexistsC>0suchthatforallballsBinRn, C-1|B|≤‖χB‖Lp(·)(Rn)‖χB‖Lp′(·)(Rn)≤C|B|. Lemma 1.4[12]Letp(x)∈B(Rn).Forany1 Lemma 1.6[21]LetΩ∈Lipγ(Sn-1),b(x)∈BMOandp(·)∈B(Rn),wehave ‖μbf‖Lp(·)(Rn)≤C‖f‖Lp(·)(Rn). Lemma 1.7[1]For everyN>0thereexistsaconstantCsuchthat and Lemma 1.8[1]SupposeV∈Bqwithq≥n/2.ThenthereexistpositiveconstantsCandk0suchthat Lemma 1.9[22]Letkbeapositiveinteger.Thenwehavethatforallb∈BMO(Rn) and alli,j∈Zwithi>j, Proof of Theorem 1.1 Fixx∈Rnand letr=ρ(x).Usingthesameideain[5]and[4],wehave ForA1,byLemma1.7,wehave Obviously, ForA3,byLemma1.7,wehave ItremainstoestimateA4.FromLemma1.7,takeN=1,weobtain Thus,usingLemma1.5andLemma1.6,wearrivethefollowinginequality andhencetheproofofTheorem1.1iscomplete. wheref0=fχB(z,2r),fi=fχB(z,2i+1r)B(z,2ir)fori≥1.Hence,wehave ByTheorem1.1,weobtain Becauseinequality(1)andLemma1.4implythatu(x,r)≥Cu(x,2r).Therefore,weobtain Furthermore,foranyi≥1,x∈B(z,r)andy∈B(z,2i+1r)B(z,2ir),wenotethat|x-y|≥|y-z|-|x-z|>C2ir.ByLemma1.7andMinkowski'sinequality,wehave UsingLemma1.8,wederivetheestimate (3) ApplyingLemma1.2andinequality(3),wegetthat Subsequently,takingthenorm‖·‖Lp(·)(Rn)andusingLemma1.9,wehave ×‖b‖BMO‖fχB(z,2i+1r)‖Lp(·)(Rn)‖χB(z,r)‖Lp(·)(Rn)‖χB(z,2i+1r)‖Lp′(·)(Rn). ApplyingLemma1.3withB=B(z,2i+1),wehave TakingN=(-[α]+1)(k0+1),weobtain Asufulfills(2)andα<0,weobtain andhencetheproofofTheorem1.2iscomplete. [1] SHEN Z. Lp estimates for Schr?dinger operators with certain potentials[J]. Ann Inst Fourier(Grenoble), 1995,45(2):513-546. [2] STEIN E M. On the functions of Littlewood-Paley, Lusin, and Marcinkiewicz[J]. Transactions of the American Mathematical Society, 1958,88:430-466. [4] GAO W, TANG L. Boundedness for marcinkiewicz integrals associated with Schr?dinger operators[J]. Proceedings-Mathematical Sciences Indian Acad Sci, 2014,124(2):193-203. [5] CHEN D, ZOU D. The boundedness of Marcinkiewicz integral associated with Schr?dinger operator and its commutator[J]. Journal of Function Spaces, Article ID402713, 10pages, 2014. [6] TANG L, DONG J. Boundedness for some Schr?dinger type operators on Morrey spaces related to certain nonnegative potentials[J]. J Math Anal Appl, 2009,355(1):101-109. [7] CHEN D, JIN F. The Boundedness of Marcinkiewicz integrals associated with Schr?dinger operator on Mmorrey spaces[J]. J Fun Spaces, Article ID901267, 11pages, 2014. [8] CHEN Y, LEVINE S, RAO M. Variable exponent, linear growth functionals in image restoration[J]. SIAM J Appl Math, 2006,66(4):1383-1406. [10] CRUZ-URIBE D, FIORENZA A, MARTELL J M, et al. The boundedness of classical operatorson variableLpspaces[J]. Annales Academiae Scientiarum Fennicae Math., 2006,31(1):239-264. [11] NEKVINDA A. Hardy-Littlewood maximal operator onLp(x)(Rn) [J]. Math Inequal Appl, 2004,7:255-265. [12] HO K-P. The fractional integral operators on Morrey spaces with variable exponent on unbounded domains[J]. Math Inequal Appl, 2013,16:363-373. [13] XUAN Z, SHU L. Boundedness for commutators of Calderón-Zygmund operator on Morrey spaces with variable exponent[J]. Anal Theory Appl, 2013,29(2):128-134. [14] ALMEIDA A, HASANOV J, SAMKO S. Maximal and potential operators in variable exponent Morrey spaces[J]. Georgian Math J, 2008,15:195-208. [15] KOKILASHVILI V, MESKHI A. Boundedness of maxmial and singular operators in Morrey spaces with variable exponent[J]. Armenian Math J, 2008,1:18-28. [16] BONGIOANNI B, HARBOURE E, SALINAS O. Class of weights related to Schr?dinger operators[J]. J Math Anal Appl, 2011,373:563-579. [17] TANG L. Weighted norm inequalities for commutators of Littlewood-Paley functionsrelated to Schr?dinger operators[J]. Archive der Mathematik, 2014,102:215-236. [18] DIENING L. Maximal function on Musielak-Orlicz spaces and generalized Lebesgue spaces[J]. Bulletin des Sciences Mathématiques, 2005,129(8):657-700. [20] ZHANG P, WU J. Commutators of the fractional maximal function on variable exponent Lebesgue spaces[J]. Czechoslovak Mathematical Journal, 2014,64(139):183C197. [21] WANG H, FU Z, LIU Z. Higher order commutators of Marcinkiewicz integrals on variable Lebesgue spaces[J]. Acta Math Scientia(Ser A), 2012,32(6):1092-1101. [22] IZUKI M. Boundedness of commutators on Herz spaces with variable exponent[J]. Rend Circ Mat Palermo, 2010,59(2):199-213. 2016-03-10 SupportedbyNSFC(11201003)andEducationCommitteeofAnhuiProvince(KJ2016A253;SKSM201602). SHU Yu(1985-), male, born in Wuhu, Anhui Province, Lecture, M.S.D. 束宇.變指數空間上與Schr?dinger算子相關的Marcinkiewica積分算子交換子[J].安徽師范大學學報:自然科學版,2016,39(6):535-541. 變指數空間上與Schr?dinger算子相關的Marcinkiewicz積分算子交換子 束 宇 (安徽商貿職業技術學院 經濟貿易系,安徽 蕪湖 241002) 在本文中,我們主要證明了變指數空間上與Schr?dinger算子相關的Marcinkiewicz積分算子交換子的有界性. Marcinkiewicz積分;交換子;Schr?dinger算子;變指數;Morrey空間 10.14182/J.cnki.1001-2443.2016.06.006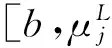
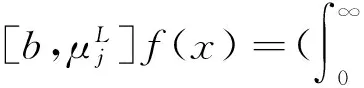
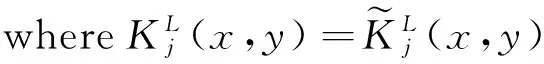
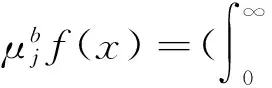
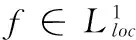
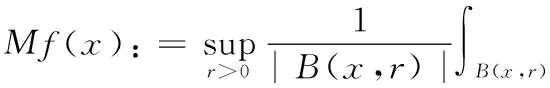
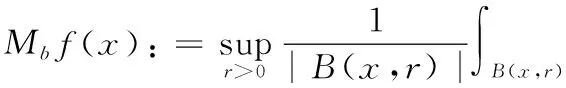
1 Results and Some Lemmas

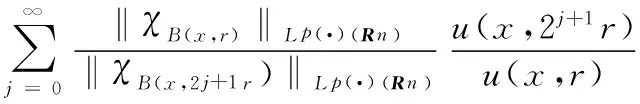
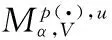
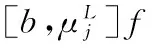
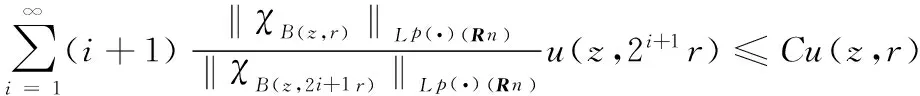
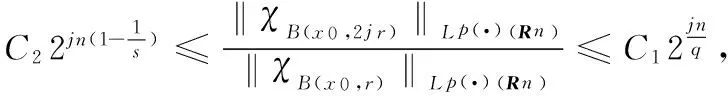
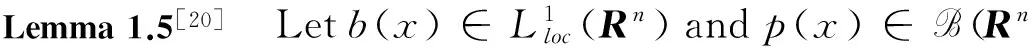
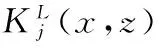
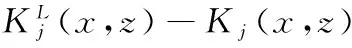
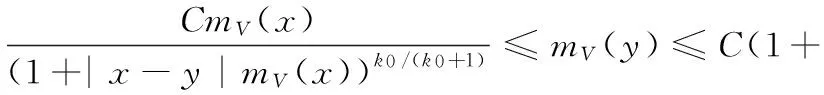
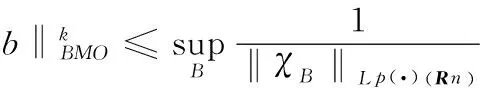
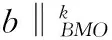
2 Proof of Theorems