有質量彈簧振子的彈簧內力

陳奎孚 黃 峰 蔣 曉 趙建柱

(1中國農業大學理學院,北京 100083; 2北京農業職業學院機電工程學院，北京 102208; 3中國農業大學工學院,北京 100083)

有質量彈簧振子的彈簧內力

陳奎孚1黃 峰1蔣 曉2趙建柱3

(1中國農業大學理學院,北京 100083;2北京農業職業學院機電工程學院，北京 102208;3中國農業大學工學院,北京 100083)

文章分析了有質量彈簧振子的彈簧內力，并用Matlab工具進行圖形化展示.分析表明：彈簧質量不可忽略時，彈簧各斷面上內力是斷面位置的函數；對振子均勻拉伸-釋放所建立的振動，彈簧內力隨時間的變化規律不再是簡諧波；隨著彈簧質量的增加，內力偏離簡諧波越來越明顯；質點質量為零時, 內力隨時間的變化規律為周期性方波.

彈簧振子；波動；偏微分方程；內力

彈簧振子是大學物理教學的經典例子.在這個經典例子中，一般都忽略不計彈簧的質量.若與質點相比，彈簧不是很輕，就需要考慮彈簧的質量.彈簧質量必須考慮的彈簧振子本質上是波動問題，研究它的工具變得復雜，相應的物理現象也復雜得多.就該問題，國內已經發表了很多文章[1-8]，朱洪玉對這一問題做了很系統的總結，對相關爭議進行了澄清[9].

需要特別指出的是：有些特性，它們在彈簧質量可忽略的情形下是顯而易見的，但在波動問題下就不那么直觀了.比如，若彈簧質量不計,則其內力并不隨彈簧的斷面位置而變化(為了表述清晰，我們把彈簧當成圓柱體，垂直于彈簧軸線的橫截面稱為彈簧的斷面)；然而，若彈簧質量必須考慮，其斷面上內力變化規律可能會很復雜.柯紅衛等研究了簡諧振動的彈簧內力[10]，但在考慮彈簧質量情形下，純簡諧振動的實現很困難，比如通常所討論的例子均勻拉伸后釋放所建立的振動，并非簡諧振動，而是多個本征振動疊加在一起的復合振動.可以推測此情形下，彈簧內力隨時間和空間的變化規律應當不會很簡單.但由于以前技術限制，大多教科書或學習輔導書往往止步于冗長的級數表達式.這樣做，一則不直觀，另則也不容易激發學生深入探究的興趣.

本文將對彈簧質量必須考慮的振子的彈簧內力進行探究，并利用數學工具軟件MATLAB的計算和圖形功能把其復雜性展示出來，讓學生對其復雜性有直觀的認識，進而促進學習興趣.

1 模型

在圖1所示的模型中，設彈簧原長為l, 勁度系數k，彈簧的質量m′均勻分布(線密度ρl=m′/l)，質點的質量為m(為了方便討論，后文經常使用質量比βm=m′/m這個參數).記位于彈簧原長x斷面的位移為u(x,t).彈簧的波動方程為[1-4](也可參照彈性桿的縱向振動[11])

ut t=v2uxx

(1)

圖1 模型

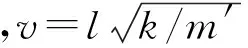
由邊界條件(2)和(3)可導出第i階無量綱本征頻率μi方程[11]

βmcosμi-μisinμi=0

(4)

無量綱本征頻率μi與有量綱的本征圓頻率ωi之間的關系為

(5)

對應的本征函數如下

(6)

2 本征振動

2.1 內力

為了與文獻[10]盡量一致，暫且假定振子發生了一階本征振動(如果要發生這樣的自由振動，必須精心控制彈簧各斷面的初位移和初速度，使得二者與第一階本征函數僅相差一個比例系數).

對這種特殊振動，彈簧各斷面的位移為

(7)

其中,A和α分別為質點的振幅和振動初相位.注意質點m最大位移是Asinμ1，而不是A.

對質量不計的輕彈簧(m′=0)，彈簧內力沿軸線不變，且等于作用在彈簧兩端的所謂“彈力”.但當質量不能忽略時，彈簧內力沿軸線變化規律正是本文要探究的問題.下面通過彈簧的局部變形來確定彈簧內力.

考慮未變形時位于x的斷面.記該斷面的局部伸縮率(在單位長度上的伸縮)為ux(ux=?u/?x)，相應的內力則能寫成κux，其中κ是與彈簧勁度系數k有關的比例系數.為了確定κ與k的關系，假定彈簧退化成無質量情形，則彈簧總伸長量(此時發生均勻變形)為lux，由彈簧胡克定律得到的彈力為k×(lux)，它也等于從局部伸縮率角度的κux.這樣得到κ=kl.利用這個關系，有質量彈簧各斷面的內力可表示為(適合于任何形式的振動)

F(x,t)=klux

(8)

將式(7)代入式(8)有

(9)

2.2 表觀勁度

通常說法“彈力與位移成正比”中：“位移”指的是質點m的位移，也就是圖1中P點位移u(l,t)；力則是彈簧作用在質點上的力，它也等于式(9)取x=l(P點)的函數值.由式(7)和式(9)可知P端的彈力與該端點位移仍成正比，但是比例系數

(10)

不再恒等于彈簧的勁度系數k.文獻[10]已指出這一點，但是文獻[10]是基于動態時彈簧仍均勻變形的假定，所得到kB與式(10)有一定差異.

kB和k的關系與μ1有關，進而與質量比βm有關.

Q端的彈力和P端質點m位移比值為

(11)

它與文獻[10]結果也有不同.

可化為

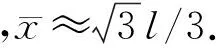
2.3 化解“佯謬”

因為動態下彈簧變形不均勻，其質心加速度üC(t)既非ü(l,t)/2，也非ü(l/2,t).正確的做法是對ü(x,t)進行積分平均得到質心加速度，即

也就是

(12)

彈簧所受合外力為

(13)

式(12)和式(13)表明彈簧運動沒有違背質心運動定理.如果都能從第一原理出發并經嚴密數學演繹，就不會出現文獻[12]的“佯謬”現象.

3 均勻拉伸模式

3.1 級數解

把彈簧準靜態地均勻拉伸到一定長度之后釋放，所形成的初條件為

對應這個初條件的振動并非簡諧振動[2,13]，從文獻[14]和[15]可以找到其級數解.這一問題在數學上完全等同于彈性桿一端帶質點的自由振動問題[16,17].上述文獻止步于位移的級數解，本文進一步探究彈簧內力特性.

采用本文的符號，各斷面的位移函數表示如下：

(16)

其中系數

(17)

將式(16)代入式(8)有

(18)

式中系數

(19)

從式(18)和式(19)可以看出彈簧的內力與x關系復雜，遠非“彈簧上各點張力變化呈線性變化”[18].

3.2 圖形展示

先看兩端Q和P處(見圖1)的力，即

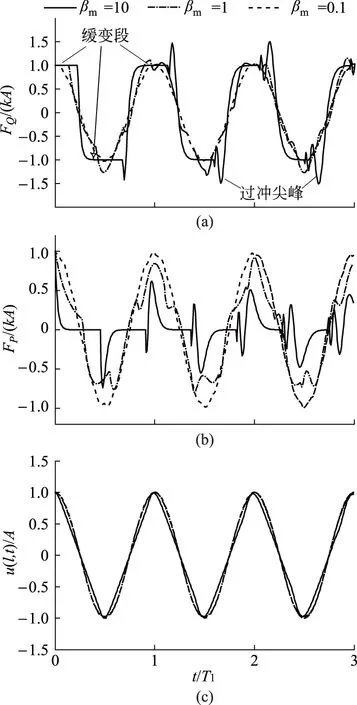
圖2 釋放初始階段的力與位移

為了直觀感受力的復雜性，使用MATLAB工具對式(20)和(21)進行了計算.兩式均為級數和，我們只能取有限項來近似.數值實驗表明，取10項即可.但為保險起見，圖2中數據是取了前5000項之和.圖2(a)和2(b)分別給出了剛釋放不久左端FQ(t)和右端FP(t).質量比選擇了βm=10(重彈簧),1和0.1(輕彈簧)3種情形.

振子的基頻(第一階頻率)與βm有關.為了方便比較，圖2中橫坐標用振子基頻所對應的周期T1作了無量綱化處理，這樣使3條曲線按照基頻的周期對齊.

圖2(a)和2(b)直觀地揭示了:βm越大，彈簧兩端受力偏離簡諧波越嚴重；隨時間增長，不規則性也越明顯.βm=10的曲線看不出有什么周期，而且有明顯的過沖尖峰(彈簧左端面在過沖尖峰的瞬間受力可超過kA).在左端面,βm=10的曲線有明顯的緩變段，這是因為處于右端的質點m釋放之后，波動的作用需要一段時間后才能傳到左端，在波動達到之前彈簧左端彈力保持不變.波動達到左端墻面后反射，再向右傳.在沒有傳出之前，也同樣存在緩變段.但是緩變段的時長因各階本征振動不同步而變短.

總之,波傳播總是需要時間的，因此只要彈簧有質量，彈簧左端力在一開始就有緩變期，只是βm越小，緩變期越短.

可以想象，隨時間增長，力的不規則性肯定會增加.圖3是1000T1～1003T1時段的變化曲線.除了時段外，圖3條件與圖2完全相同.圖3的不規則性更加明顯.如果βm比較小，變化曲線還是接近正弦波的，就如同文獻[19]所報告的“位移、速度、加速度和力隨時間的變化曲線,……,它們與理想的正弦曲線是接近的”，因為該文最大的βm為105.10/(11.98+80)=1.1426(當然實驗測量電路一般都有低通濾波環節，它也會抑制高頻波動).

為了體會介于Q和P之間內力的復雜性，圖4用瀑布圖的方式顯示了沿軸線均勻分布的21個斷面上內力隨時間變化曲線(βm=10).圖中x坐標對應斷面的位置.圖4(a)中最前面(x=0)一條粗線就是圖2(a)中實線，而最后面(x=l)的粗線就是圖2(b)中的實線.從該圖可以體會內力的復雜性.在波動從P端向Q端傳遞過程中，圖2(a)所標注的緩變段在Q點最長，而越靠近P點越短，這是因為波動來的越早.圖4(b)與圖3對應，可看出隨時間增長，內力的不規則性非常明顯.

3.3 定性解釋

再回到圖2.與力相比，圖2(c)的質點位移曲線較為規則，盡管它也是無窮多個本征振動累加.數學上，圖2和圖3(c)通過數學式(8)與各自(a)和(b)聯系起來.圖3(c)圖對整個彈簧變形的空間積分，而積分有平滑作用，即把頻率高(對應高階本征振動)的波動平滑掉，所以右端點的位移曲線較光滑.(a)和(b)兩圖反映內力，與局部伸縮率成正比.而局部伸縮率是位移對空間的微分，會突出頻率高的成分.

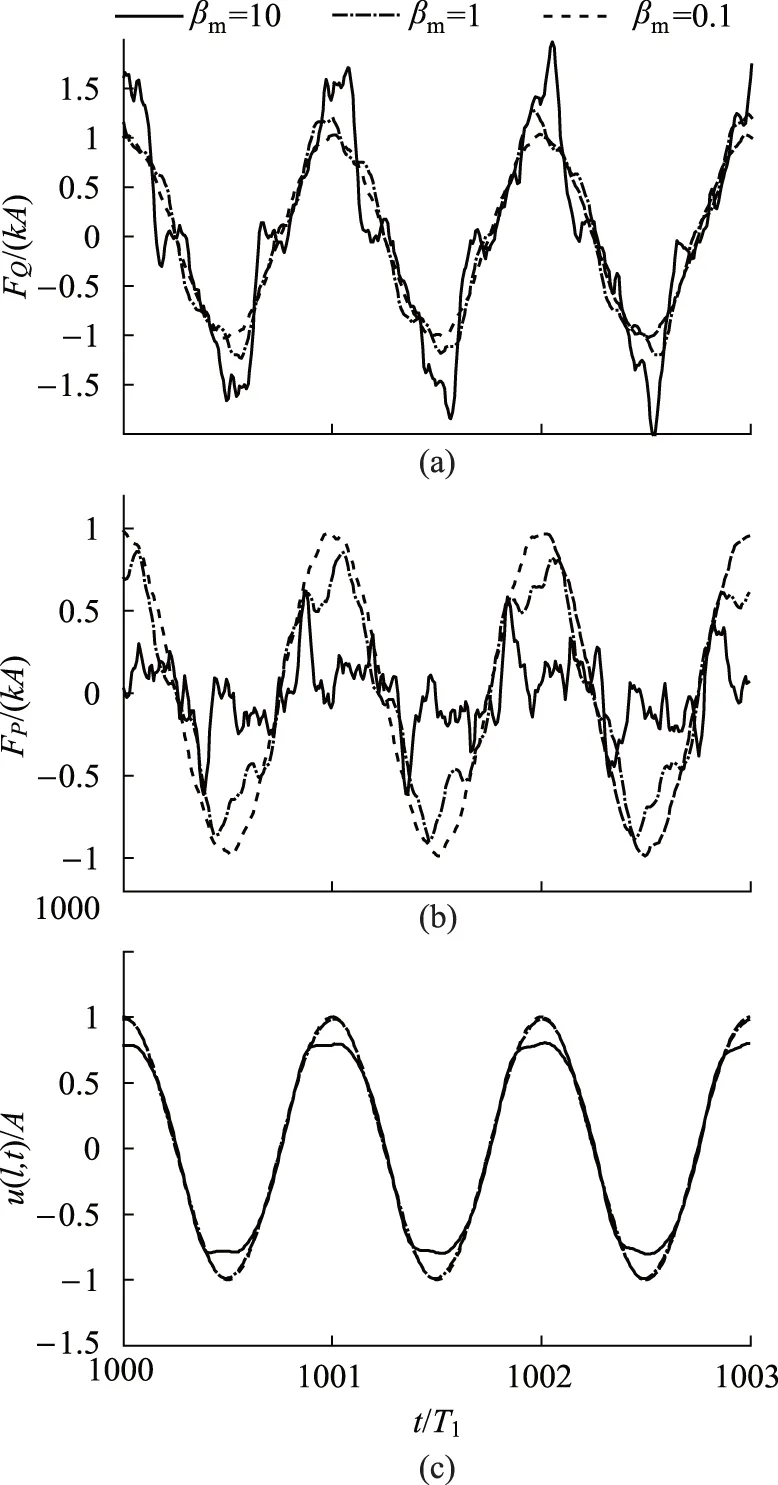
圖3 釋放長時間后的力與位移

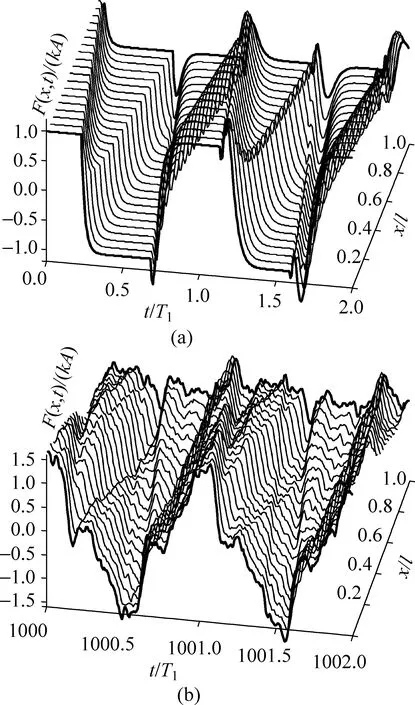
圖4 內力復雜性

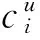
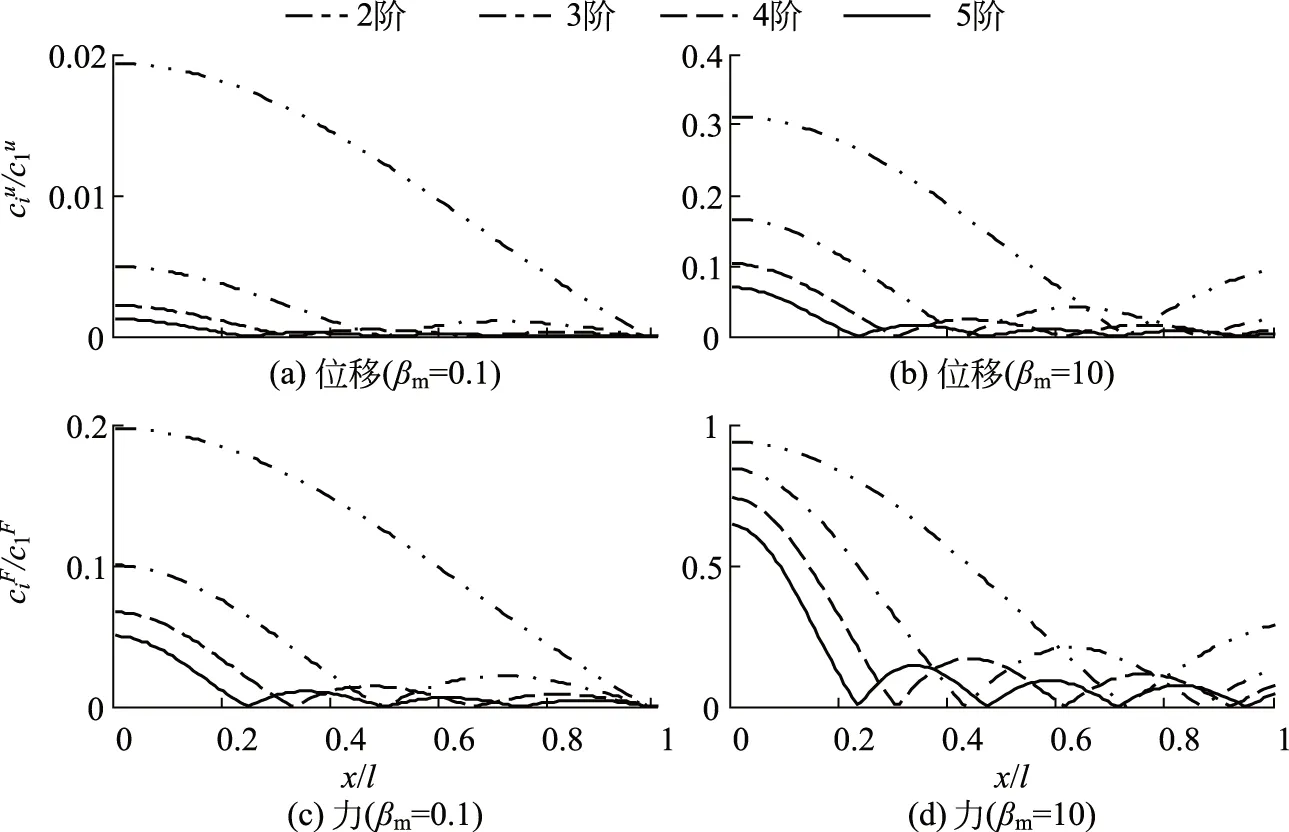
圖5 非基頻本征函數的貢獻

為了對收斂速度有個直觀體會，圖5顯示了位移和力的前2～5階系數與基頻系數比值.當質量比βm相對較小時(βm=0.1)，無論是力，還是位移，非基頻的系數都比較小(圖5(a)和圖5(c)).圖5(b)和圖5(d)的βm比較大(βm=10，即質點質量只有彈簧質量的1/10)，此時位移第二階系數可達基頻的31%,力的第二階系數可達基頻的94%.顯然，若βm比較大，就必須考慮高階本征函數的貢獻.

4 純彈簧情形

4.1 位移

當質點m=0，振子只剩下彈簧了.此時βm=m′/m→∞.從式(4)可解出

μi=iπ/2

(22)

代入式(18)有

(23)

利用三角函數的積化和差公式，也可以將式(23)表示成方向相反的行波疊加

u(x,t)=R(x+vt)+R(x-vt)

(24)

其中

(25)

可以驗證R(x)是周期為4l的三角波，如圖6所示.

4.2 內力

彈簧內力為

F(x,t)=kl[R′(x+vt)+R′(x-vt)]

(26)

因為R(x)是分段函數，我們也必須對F(x,t)作分段處理.F(x,t)是以4l/v為周期的周期函數，故只需研究一個基本周期內的特性，因此時間限制為0≤t≤4l/v，而x的限制為0≤x≤l.在這兩個限制下，x-vt應小于-4l而大于l.這個范圍有兩個分段點，即x-vt=-l,-3l，也就是t=(x+l)/v,(x+3l)/v.而對x+vt也有兩個分段點，t=(l-x)/v和t=(3l-x)/v.再把周期邊界的t=0和t=4l/v兩個點加上，于是在基本周期內有6個關鍵點，它們把一個基本周期分成5段.相關信息匯總于表1.

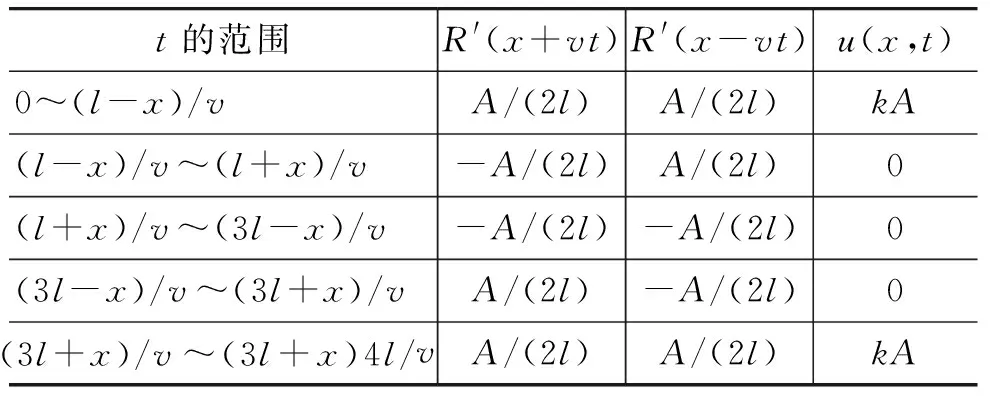
表1 彈簧內力

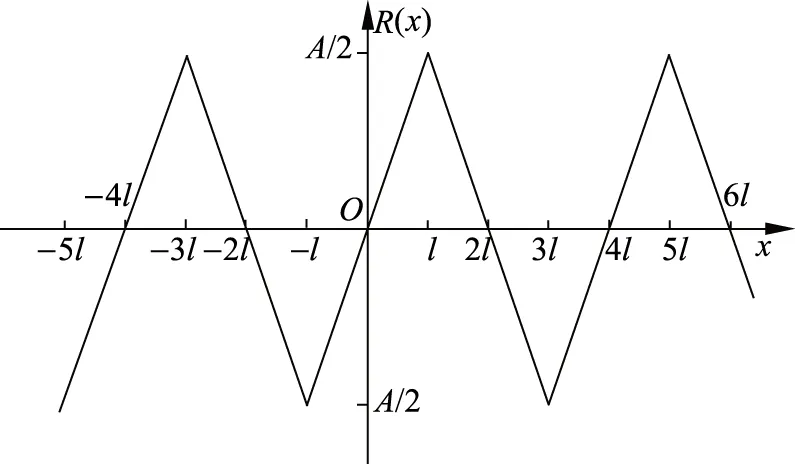
圖6 行波波形

圖7畫出了x=0,l/4,l/2和3l/4共4個斷面內力在一個基本周期內變化.x=0對應彈簧的左端，該處的內力不是拉，就是壓，而在其他斷面處彈簧存在不受力的狀態，這是因為在該時段此斷面無彈性波.此外各斷面內力隨時間變化呈不連續的方波.

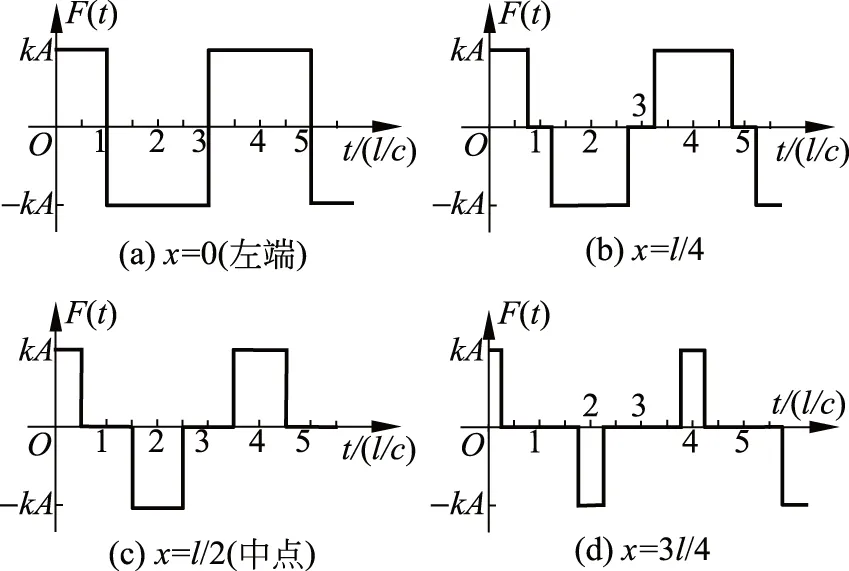
圖7 質點質量為零情形的彈簧內力

4.3 驗證牛頓第二定律

質心的加速度為

即

根據圖6,R′(x)為偶函數，所以第二項和第四項都等于-R′(vt).第三項為R′(l-vt)=R′(vt-l).再根據圖4可知R′(vt-l)=-R′(vt+l)，故而上式的第一項和第三項相抵消.最后有

üC(t)=-2v2l-1R′(vt)

與式(26)取x=0相比較，同樣可知質心運動也沒有違背牛頓定律(注意加速度正方向指向右，而按內力方向規則，彈簧左端的內力向左，從而上式右端有負號).

5 結語

彈簧質量振子是物理教學的經典模型.該模型相關知識的挖掘和積累，對豐富課堂教學、促進探究性學習仍具有現實意義.本文針對典型情形，就有質量振子的彈簧內力，進行了詳細的探究.典型的情形包括本征振動，彈簧均勻拉伸-釋放所建立的振動等.

研究發現振子的內力與相關文獻所聲稱的有差異，而彈簧均勻拉伸-釋放所建立的自由振動也不是簡諧振動，尤其是內力偏離簡諧更明顯.彈簧質量越大，內力偏離簡諧波越嚴重.用MATLAB工具以圖形展示了這種不規則性.當質點質量零時，內力變成時間的周期性方波函數.

[1] 丁履成,司明揚.有質量的彈簧的振動問題[J].大學物理,1985,4(9):15-18.

[2] 劉大鵬,關榮華.彈簧質量對彈簧諧振子圓頻率的影響[J].大學物理,1995,14(10):22-24.

[3] 于鳳軍,王春明.彈簧系統振動周期的近似公式[J].大學物理,2012,31(3):13-15.

[4] 沈鐘偉,張峰.彈簧質量對振動周期的影響[J].大學物理,2013,32 (3):44-45.

[5] 王鋒, 唐國金.考慮彈簧質量的振子精確解[J].物理與工程,2003,13(2):28-30.

[6] 何連超.有質量彈簧的振動周期探討[J].物理與工程,2011,21(5):1-2.

[7] 任保文.彈簧的振動[J].物理與工程,2014,24(1):19-21.

[8] 陳奎孚,賈貴儒,黃峰.對有質量彈簧的振子基頻作近似的若干算法之比較[J].大學物理,2014,33(8):18-20.

[9] 朱洪玉.關于質點彈簧系統在重力作用下的靜平衡與振動[J].大學物理,2009,28(1):1-10.

[10] 柯紅衛,劉坦,趙耀.有質量彈簧的振動與彈性力[J].大學物理,2013,32(5):17-18.

[11] 陳奎孚.機械振動基礎[M].北京:中國農業大學出版社,2011:312-318.

[12] 田蓬勃,趙強.彈簧振子佯謬[J].物理與工程,2002,12(1):12-13.

[13] 黃兆梁.對有質量彈簧的振子系統振動周期的探討[J].大學物理,2011, 30(5):32-34.

[14] 徐世良.數學物理方法解題分析[M].南京:江蘇科學技術出版社,1983:519-527.

[15] 陳奎孚,付志一,高陽.彈簧質量不能忽略的振系之自由振動[C].北京力學會.第20屆學術年會論文集, 北京,2014：640-644.

[16] 林瓊桂.與質點連結的彈性桿的振動[J].大學物理,2004,23(3):18-20.

[17] 徐建軍,胡嗣柱.用Laplace變換法求解端點系有集中質量的彈性桿的振動問題[J].大學物理,2004,23(12):12-17.

[18] 于秀安.計算有質量彈簧的形變量[J].技術物理教學,2013,21(2):85-86.

[19] 褚幼令,陳乃東,王摯平.彈簧振子振動特性的計算機實時測量[J].大學物理,1998,17(5):32-34.

■

THE SPRING’S INTERNAL FORCE OF THE VIBRATOR WITH A MASSIVE SPRING

Chen Kuifu1Huang Feng1Jiang Xiao2Zhao Jianzhu3

(1College of Science, China Agricultural University, Beijing 100083;2Schools of Mechanical & Electrical Engineering, Beijng Vocational College of Agriculture, Beijing 102208;3College of Engineering, China Agricultural University, Beijing, 100083)

The spring’s internal force of a vibrator with a light spring is trivially a constant, while the case with a massive spring is much sophisticated. This problem was investigated in detail, and was visualized by the mathematical tool Matlab. This study shows, firstly, that the spring’s internal force varies along the spring’s length for a massive spring case. Secondly, the vibration established by uniformly stretching and releasing the spring is not a simple harmonic motion; as a result, the spring’s internal force deviates from the simple harmonic pattern. Thirdly, the deviation is more and more significant as the spring mass increases. Finally, the internal force lends itself to be a square wave when the lumped mass is null.

mass-spring vibrator; wave motion; partial differential equations; internal force

2015-06-03；

2016-02-28

2015年度北京高等學校教育教學改革立項項目(編號：2015-ms049;名稱：以工程教育認證為導向的車輛工程專業實踐教學改革研究與實踐).

陳奎孚,男，教授.從事力學和振動的教學與研究.chenkuifu@cau.edu.cn

趙建柱，男，副教授.主要研究方向為車輛動力學.zhjzh@cau.edu.cn

陳奎孚,黃峰,蔣曉,等. 有質量彈簧振子的彈簧內力[J]. 物理與工程，2016，26(5)：6-11，15.