一道聯賽預賽題引發的思考

?

一道聯賽預賽題引發的思考

湖北省武昌實驗中學(430061)彭景

問題1ΔABC中，AB=BC=2,AC=3,

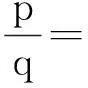
上述問題1為2012年全國高中數學聯賽湖北省預賽試題.本文在此將給出上述問題的一般化探究，同時對三角形的外心、重心、垂心等類似問題作進一步探究，希望對讀者有所幫助.

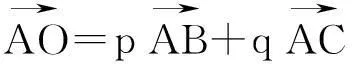
ΔABC中，AB=c,BC=a,AC=b,我們不妨提出如下更一般性的問題：

事實上，對于問題2，我們有如下結論：

圖1

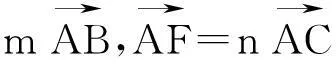
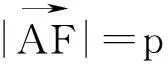
大家知道，三角形的四心(重心、內心、外心、垂心)常常作為各級各類考試的熱點問題，類似于問題2，我們不禁提出如下問題：

對于上述問題，類似于結論2，我們也可得到如下結果：

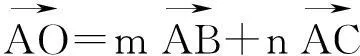
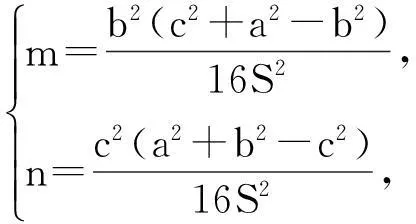
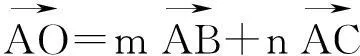
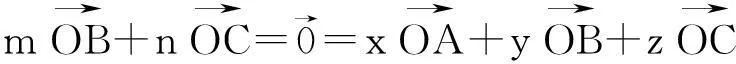
故此時x∶y∶z=a2(b2+c2-a2)∶b2(c2+a2-b2)∶c2(a2+b2-c2).

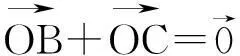
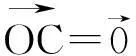
綜上所述，若O為ΔABC的外心，則x∶y∶z=a2(b2+c2-a2)∶b2(c2+a2-b2)∶c2(a2+b2-c2).

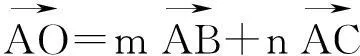
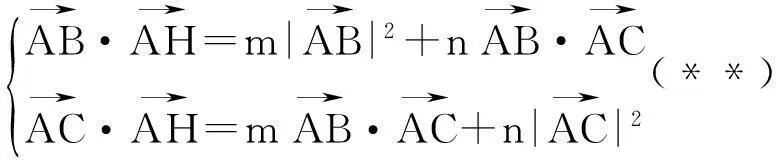
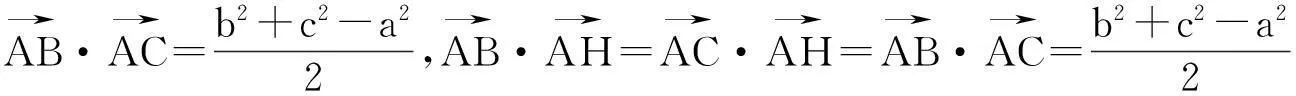
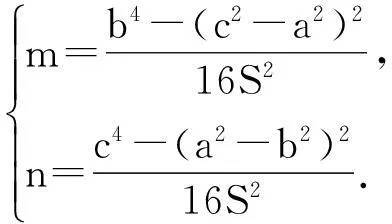
不難驗證此時x∶y∶z=[a4-(b2-c2)2]∶[b4-(c2-a2)2]∶[c4-(a2-b2)2].