積分型粘彈性阻尼器耗能結構瞬態響應的精確解

李創第，尉霄騰,王磊石，鄒萬杰

(1.廣西大學土木建筑工程學院， 廣西南寧530004；2.廣西科技大學土木建筑工程學院， 廣西柳州545006)

?

積分型粘彈性阻尼器耗能結構瞬態響應的精確解

李創第1,2，尉霄騰1,王磊石1，鄒萬杰2

(1.廣西大學土木建筑工程學院， 廣西南寧530004；2.廣西科技大學土木建筑工程學院， 廣西柳州545006)

摘要：為建立積分型粘彈性阻尼器耗能結構的精確設計方法，對單自由度結構在任意激勵和非零初始條件下的時域瞬態響應精確解進行了系統研究。首先采用線性粘彈性阻尼器的一般積分型精確分析模型，用微分積分方程實現了單自由度結構的時域非擴階精確建模；然后采用傳遞函數法，直接在耗能結構非擴階空間上獲得了變頻耗能結構在任意激勵和非零初始條件下位移與速度時域瞬態響應的解析表達式；最后，基于此精確解得到了結構在平穩Kanai-Tajimi譜隨機地震激勵下響應方差的解析表達式。通過與擴階復模態法結果的對比分析，驗證了所獲精確解的正確性和簡易性，表明建立了適用于單自由度積分型粘彈性阻尼器耗能結構的優效解析方法。

關鍵詞：傳遞函數法；一般積分型模型；瞬態響應精確解；隨機響應精確解

0引言

橡膠支座基礎隔震[1]和耗能減震是目前兩種最為成熟有效的被動控制技術。線性粘彈性阻尼器是一種性能優良的耗能裝置，在抗震工程中應用廣泛。

一般積分型模型[2-3]是粘彈性阻尼器的最一般模型，其他模型如復模量模型[4]、分數導數模型[5-7]、一般微分型及其近似模型[2]等均為該模型的近似或無限逼近。

目前粘彈性耗能變頻結構的分析方法主要分為擴階精確法和非擴階近似法兩類。擴階精確法針對廣義Maxwell[8]、GHM[9]、分數導數Kelvin[10]等易于擴階粘彈性近似模型，利用擴階復模態法獲得結構響應解析解。因物理意義不明確，變量個數劇增，計算效率低，使該方法難以用于耗能結構基于反應譜的設計與研究。

非擴階近似法主要是模態應變能法[11]和取結構基頻的強行振型解耦法[12-13]，但近似法采用阻尼器頻域建模方式，使耗能結構方程并不嚴格適用于地震和強風等非簡諧激勵的時域分析，且采用較多近似假設，使其精度和適用范圍有待提高[14-16]。

針對傳統方法的不足，本文力求得出兼顧精確和效率的優效方法。傳遞函數法不用擴階運動方程，可直接獲得一般粘滯阻尼對稱線性定常系統的脈沖響應矩陣的精確解，但尚未見該方法用于粘彈性阻尼變頻非定常結構的研究。基于傳遞函數法，本文成功獲得了單自由度積分型粘彈性阻尼器耗能結構的精確設計方法，通過與復模態方法對比，驗證了該方法的正確性與簡易性。

1運動方程

設置一般線性粘彈性阻尼器的單自由度結構的動力方程可表示為：

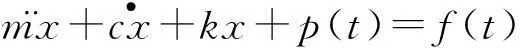
粘彈性阻尼器作用力p(t)與位移x(t)的一般積分型本構關系為[17]：

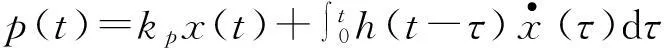
式中：kp和h(t)分別為阻尼器的平衡模量和松弛函數。

故單自由度一般線性粘彈性阻尼器耗能結構的時域動力方程均可精確表示為：

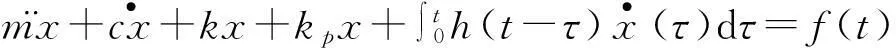
(1)

方程(1)具有一般性，既可表示任意單自由度線性粘彈性阻尼器耗能結構方程，也可表示任意單自由度線性粘彈性材料組合結構方程[18]。

2結構瞬態響應的傳遞函數法

2.1結構特征值分析

對運動方程(1)取拉氏變換，得：

也即：

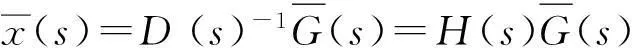
(2)

其中，

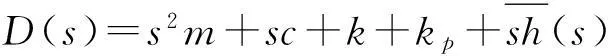
(3)

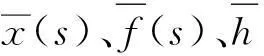
結構的特征值方程即為：

D(s)=0。

(4)

由式(4)可得出結構的N=2+n個特征值sj，包括有1對共軛復特征值和n個實特征值。

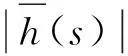
2.2傳遞函數解析式

由于結構特征值sj為傳遞函數的極點，故傳遞函數可展開為：

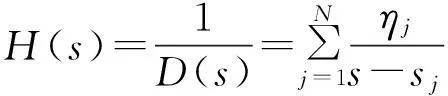
(5)

所以

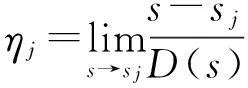
由洛必達法則，計算常數ηj為：

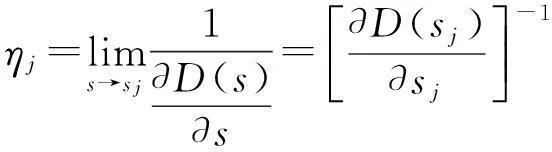
(6)

又因

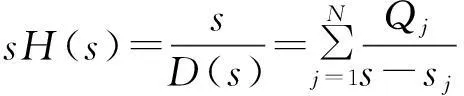
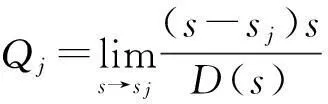
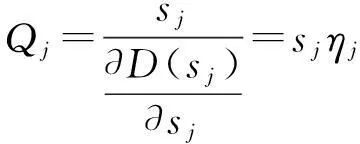
故有

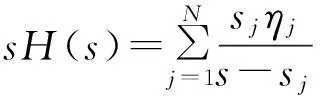
(7)

2.3結構位移和速度瞬態響應的解析解

由式(2)、式(3)和式(5) 、式(7)可得：

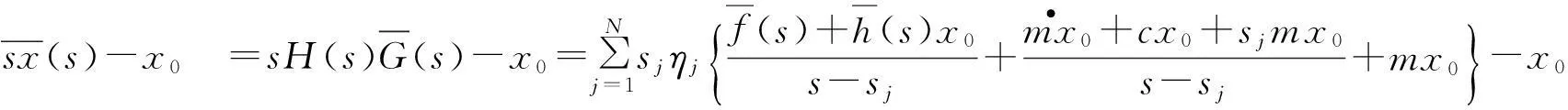
對以上兩式進行拉氏變換，可得

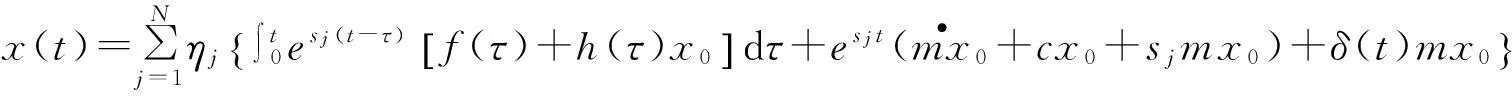
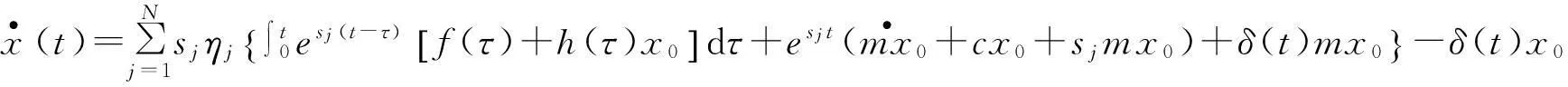
式中，δ(t)為狄拉克函數。

對于t>0時，結構位移與速度響應可進一步表示為：

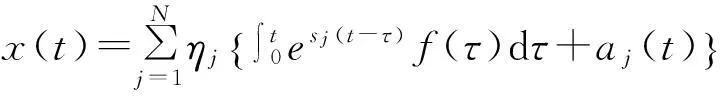
(8)

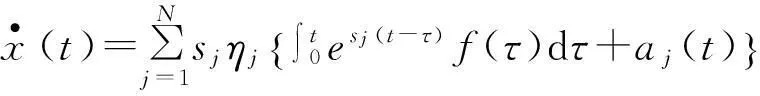
(9)

式中，aj(t)表示由初始條件產生的響應影響，且

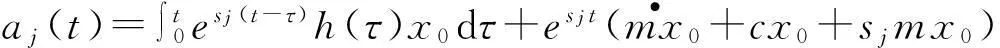
(10)

顯然，對于零初始條件，aj(t)=0，(j=1～N)。

結構響應解析解表達式(10)完全類似于粘滯阻尼結構用經典復模態法所獲得的響應表達式，可視粘滯阻尼定常結構經典復模態法在粘彈性耗能變頻結構的推廣。

3解析解的驗證分析

對比單自由度廣義Maxwell粘彈性阻尼減震結構響應的復模態法分析結果，驗證本文方法的正確性。

3.1單自由度廣義Maxwell阻尼減震結構方程

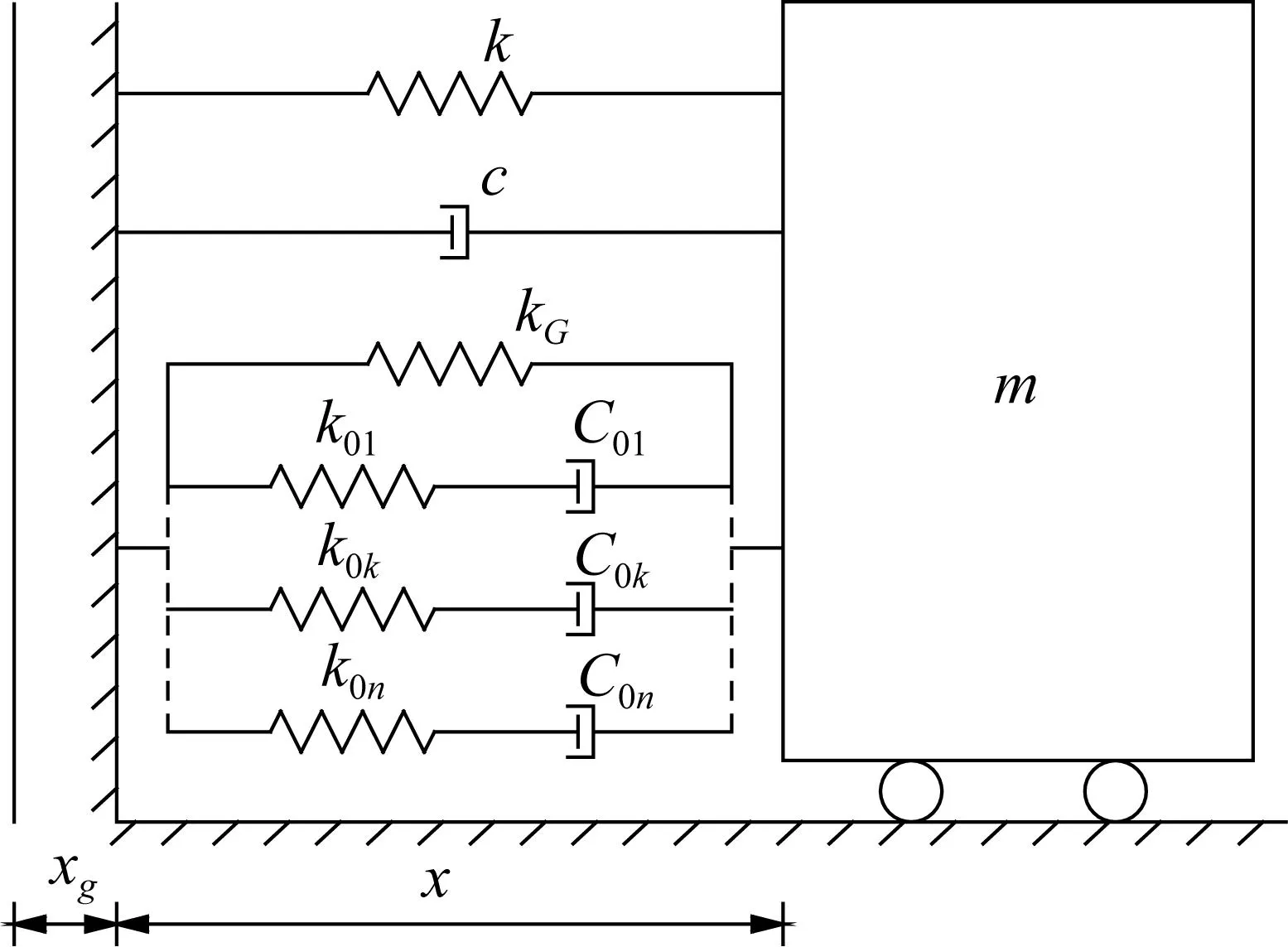
圖1　單自由度廣義Maxwell阻尼器耗能結構Fig.1　SDOF (single degree of freedom)energy dissipation structure withgeneralized Maxwell damper

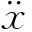
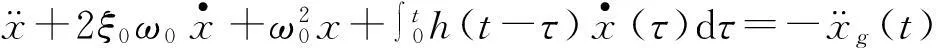
(11)

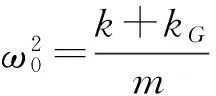
3.2本文方法結果

由式(4)，結構特征值方程為：

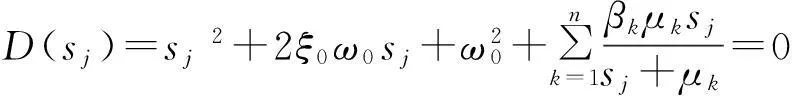
(12)

根據式(12)可得結構2+n個特征值sj。

由式(6)，計算常數ηj為：

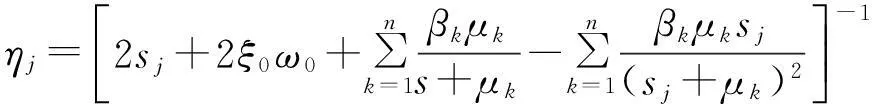
(13)

則在零初始條件下，由式(8)結構的位移和速度響應分別為：

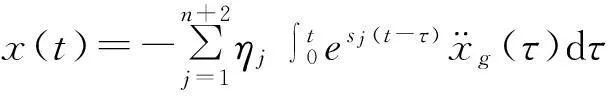
(14)

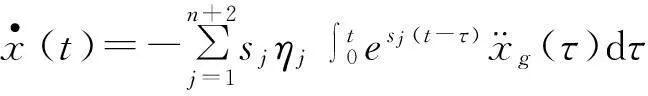
(15)

3.3復模態法結果

令中間變量：

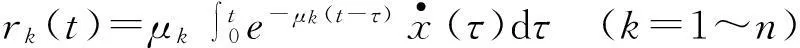
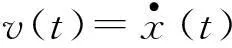
則運動方程(11)可擴階為如下一階狀態方程組：

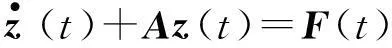
(16)

式中：

z(t)=[x(t),v(t),r1(t),…,rn(t)]T，

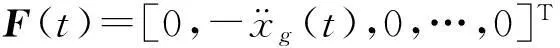
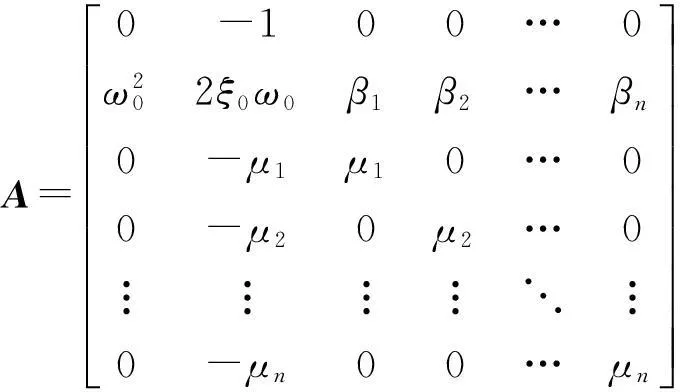
方程(16)的特征根方程及特征根所對應右、左復模態向量方程分別為：

det[Iλj+A]=0，

(17)

[Iλj+A]φj=0，

[Iλj+A]Tψj=0。

由數學歸納法不難驗證特征值方程式(12)與特征值方程式(17)完全一致，即λj=sj。同時，可求出右、左復模態向量分別為：

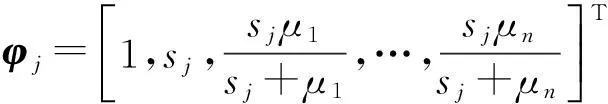
(18)

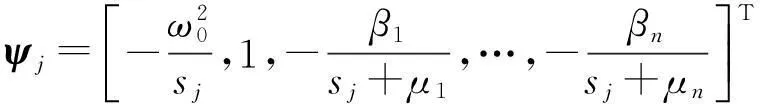
(19)

由式(18)、式(19)和式(13)不難驗證：

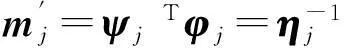
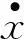
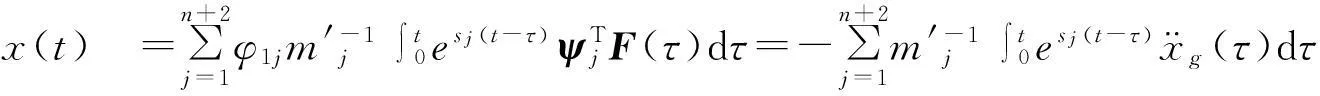
(20)

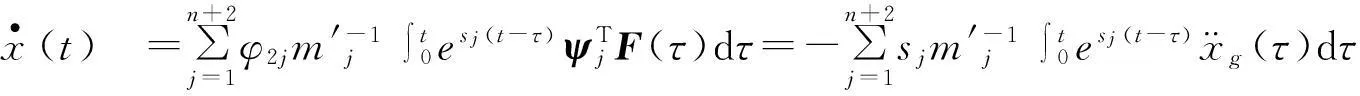
(21)

式中： φ1j和φ2j分別為φj的第一、二個分量。

對比式(14)、式(15)和式(20)、式(21)知，兩種方法計算結果完全相同，但本文方法計算簡便，適用范圍更廣。

4耗能結構平穩隨機地震響應的精確解

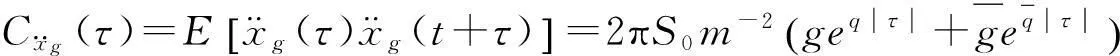
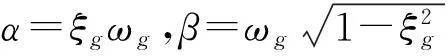
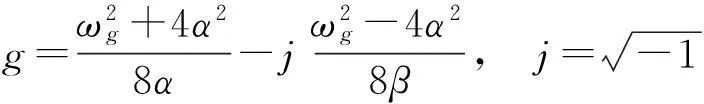
式中：ωg、ξg分別表示場地土的卓越頻率和阻尼比；S0為基巖上白噪聲的譜強度因子。

由式(8)、式(9)，有：

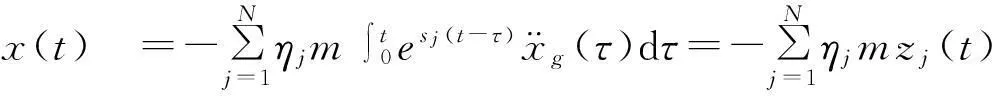
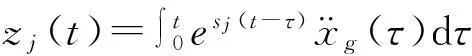
故：

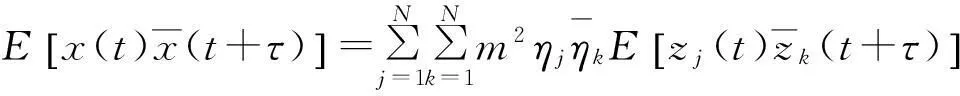
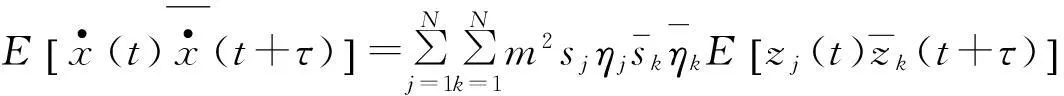
由復模態理論[19]，可以獲得z(t)的協方差函數為：

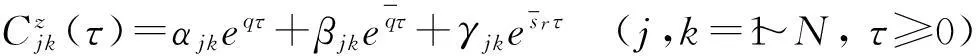
其中：

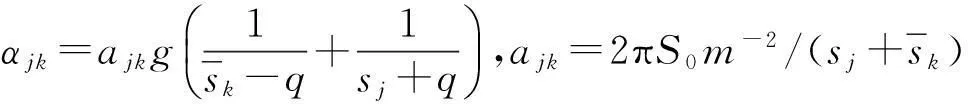
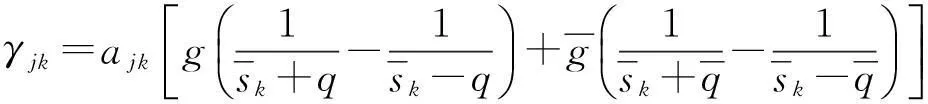
由式(16)可得：

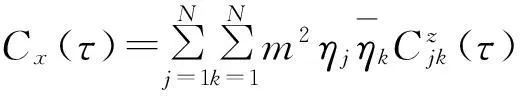
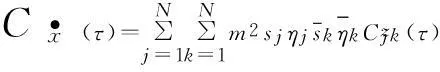
令τ=0，得結構的位移、速度響應的方差分別為：

E[x2(t)]=Cx(0)，

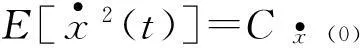
5算例分析

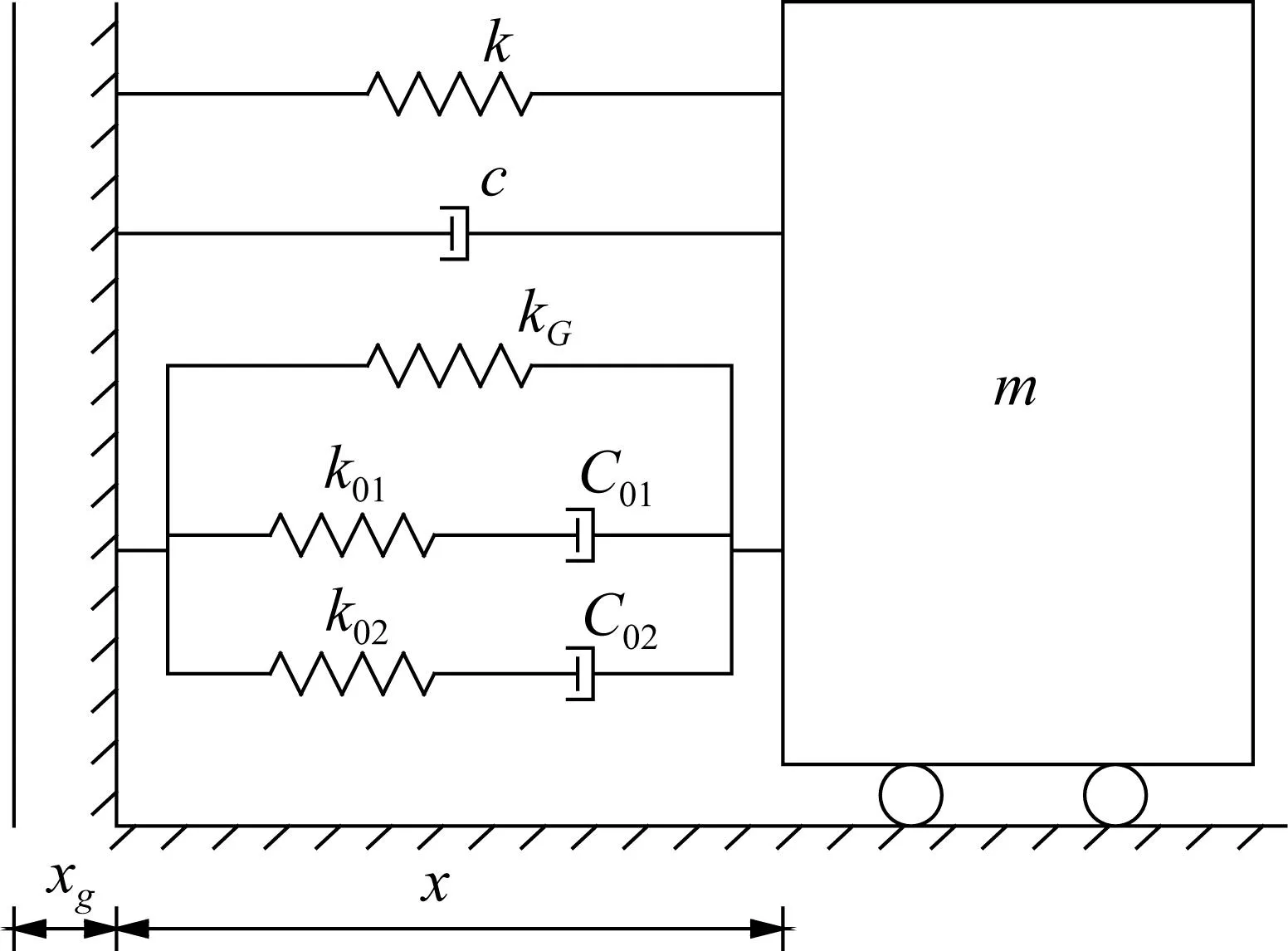
圖2　計算簡圖Fig.2　Calculation diagram

對于如圖2所示的質量為m，剛度為k，阻尼為c的單自由度廣義Maxwell阻尼減震結構，結構所在地區的抗震設防烈度為I=8度(0.2 g)。計算參數為：結構質量m=1kg，結構剛度k=300N/m，阻尼比取ξ0=0.05，結構自振頻率ω0=20s-1；兩個并聯的Maxwell阻尼器性能參數分別為：平衡模量kG=100N/m，松弛時間倒數μ1=10s-1，μ2=15s-1，單元阻尼系數分別取c01=18、24、30、36N·s/m，c02=12、16、20、24N·s/m。采用中等堅硬度土壤參數，場地土的卓越頻率和阻尼比分別取ωg=16.5s-1，ξg=0.8，譜強度S0=0.013 87m2/s3。所得特征值示于表1；所得計算常數ηj示于表2；系統位移方差和速度響應方差示于表3。

表1　特征根計算結果

表2　ηj計算結果

表3　響應方差計算結果

表1、表2給出了結構特征值及計算參數ηj的計算結果；由表3所示結果可知，隨著阻尼器的單元阻尼系數增大，阻尼耗能結構的位移和速度響應方差有減小的趨勢，表明適當調整阻尼器的阻尼單元性能參數，可以減小結構的地震反應劇烈程度，使結構響應更趨于平穩；計算結果與實際情況相符，驗證了本文分析方法的可行性。

8結論

本文對一般積分型單自由度粘彈性阻尼耗能減震結構在任意激勵和非零初始條件下的瞬態響應精確解進行了系統研究。首先采用線性粘彈性阻尼器一般積分型精確分析模型，用微分積分方程實現了結構的時域非擴階精確建模；然后采用傳遞函數法，直接在耗能結構非擴階空間上獲得了變頻耗能結構在任意激勵和非零初始條件下位移與速度時域瞬態響應的解析表達式；基于廣義Maxwell阻尼器模型，通過對比傳統經典擴階復模態法的分析求解過程與所得響應解析表達式，驗證了該精確解的正確性和簡易性。此振動機理將為建立耗能變頻結構精確的振型分解反應譜法提供分析路徑。最后，基于結構瞬態響應的精確解，得到了結構在Kanai-Tajimi譜平穩隨機地震激勵下的響應方差的解析表達式，并通過算例反映了阻尼器參數對結構響應隨機特性的影響，驗證了本文方法的可行性。本文為一般積分型單自由度粘彈性阻尼耗能結構瞬態響應與隨機響應的分析研究提供了一條有效途徑，同時為一般積分型多自由度粘彈性阻尼耗能結構瞬態響應與隨機響應的分析奠定了一定的理論基礎。

參考文獻：

[1]李創第, 陳歐陽, 葛新廣，等.多層隔震結構近似實空間解耦及地震作用取值[J]. 廣西大學學報(自然科學版), 2013, 38(4):785-794.

[2]PARK S W.Analytical modeling of viscoelastic dampers for structural and vibration control [J]. International Journal of Solids and Structures, 2001, 38: 8065-8092.

[3]李創第，鄒萬杰，葛新廣,等.多自由度一般積分型粘彈性阻尼器減震結構的隨機響應與等效阻尼[J]. 工程力學，2013，30(4)：136-145.

[4]CHANG K C, LIN Y Y.Seismic response of full-scale structure with added viscoelastic dampers [J]. Journal of Structural Engineering, 2004, 130(4): 600-608.

[5]HWANG J S, WANG J C.Seismic response prediction of HDR bearings using fractional derivative Maxwell model [J]. Engineering Structures, 1998, 20: 849-856.

[6]APTILE A, INAUDI J A, KELLY J M.Evolutionary model of viscoelastic dampers for structural applications [J]. Journal of Engineering Mechanics, 1997, 123(6): 551-560.

[7]LEWANDOWSKI R, CHORAZYCZEWSKI B.Identification of the parameters of the Kelvin-Voigt and Maxwell fractional models used to modeling of viscoelastic dampers [J]. Computers and Structures, 2010, 88: 1-17.

[8]ZHANG J, ZHANG G T.The Biot model and its application in viscoelastic composite structures [J]. Journal of Vibration and Acoustics, 2007, 129: 533-540.

[9]TRINDADE M, BENJEDDOU A, OHAYOU R.Modeling of frequency-dependent viscoelatic materials for active-passive vibration damping [J]. Journal of Vibration and Acoustics, 2002, 122: 169-174.

[10]CHANG T, SINGH M P.Seismic analysis of structures with a fractional derivative model of viscoelastic dampers [J]. Earthquake Engineering and Engineering Vibration, 2002, 1(2): 251-260.

[11]JOHNSON C D.KIENHOLA D A.Finite element prediction of damping in structures with constained viscoelastic layers [J]. AIAA Journal, 1982, 20(9): 1284-1290.

[12]歐進萍，吳斌，龍旭.耗能減振結構的抗震設計方法[J]. 地震工程與工程振動，1998，19(2)：98-107.

[13]OU J P, LONG X.LI Q S.Seismic response analysis of structures with velocity-dependent dampers [J]. Journal of Constructional Steel Research, 2007, 63: 628-638.

[14]PALMERI A, RICCIARDELLI F.Fatigue analysis of building with viscoelastic dampers [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94: 377-395.

[15]PALMERI A.Correlation coefficients for structures with viscoelastic dampers [J]. Engineering Structure, 2006, 28: 1197-1208.

[16]TSAI M H, CHANG K C.Higher-mode effect on the seismic response of building with viscoelastic dampers [J]. Earthquake Engineering and Engineering Vibration, 2002, 1(1): 119-129.

[17]李創第，鄒萬杰，葛新廣,等.多自由度一般積分型粘彈性阻尼器減震結構的隨機響應與等效阻尼[J]. 工程力學，2013，30(4)：136-145.

[18]ZHANG J, ZHANG G T.The Biot model and its application in viscoelastic composite structures [J]. Journal of Vibration and Acoustics, 2007, 129: 533-540.

(責任編輯唐漢民梁健)

Exact transient response solution of energy dissipation structure with internal viscoelastic damper

LI Chuang-di1,2, WEI Xiao-teng1, WANG Lei-shi1, ZOU Wan-jie2

(1.College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China;

2.Department of Civil Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China)

Abstract:In order to establish an accurate design method for general linear viscoelastic damping energy dissipation structures, a systematically research on the time domain transient response exact solution of structure that have single degree of freedom was conducted under arbitrary excitation and non-zero initial condition. A general integral accurate analysis model of linear viscoelastic damper was adopted, and a precise non-extended order model in time domain of structure that had SDOF(single degree of freedom) was created by applying the differential-integral equation. The transient displacement and velocity response analytical expressions of variable frequency energy dissipation structure in time domain under arbitrary excitation and non-zero initial condition were obtained directly in non-extended order space of energy dissipation structure using the transfer function method. The analytical expression of response variance of structure that met with stationary random seismic excitation of Kanai-Tajimi spectrum was established by applying the exact solution obtained in this paper. It is proved that this exact solution is correct and simple, compared with the consequences obtained by employing the complex model method of extended order, which suggests that an effective analytical solution has been built and the solution is applicable to general linear viscoelastic damping energy dissipation structures of SDOF.

Key words:transfer function method; general integral model; exact solution of transient response; exact solution of random response

中圖分類號：TU311.3

文獻標識碼：A

文章編號：1001-7445(2016)01-0083-08

doi:10.13624/j.cnki.issn.1001-7445.2016.0083

通訊作者：李創第(1964—)，男，廣西柳州人，廣西科技大學教授，博士； E-mail：lichuangdi1964@163.com。

基金項目：國家自然科學基金資助項目(51468005)；廣西自然科學基金項目(2014GXNSFAA118315)；廣西科技大學創新團隊支持計劃項目

收稿日期：2015-04-20；

修訂日期：2015-11-24

引文格式：李創第，尉霄騰,王磊石,等.積分型粘彈性阻尼器耗能結構瞬態響應的精確解[J].廣西大學學報(自然科學版)，2016，41(1)：83-90.