遺傳算法優(yōu)化的非線性鋼結(jié)構(gòu)模糊控制研究

張永兵，梁星云，唐　瀅，陳立星

(廣西大學(xué)土木建筑工程學(xué)院， 廣西南寧530004)

?

遺傳算法優(yōu)化的非線性鋼結(jié)構(gòu)模糊控制研究

張永兵，梁星云，唐瀅，陳立星

(廣西大學(xué)土木建筑工程學(xué)院， 廣西南寧530004)

摘要：采用遺傳算法優(yōu)化模糊控制算法的隸屬函數(shù)及比例因子，通過(guò)壓電變摩擦阻尼器實(shí)現(xiàn)減少非線性鋼結(jié)構(gòu)的地震響應(yīng)。采用雙輸入單輸出的模糊控制器，選取結(jié)構(gòu)的層間位移的絕對(duì)值、層間速度的絕對(duì)值作為模糊控制器的輸入變量，輸出變量為作用電壓，選取三角形函數(shù)作為輸入、輸出變量的隸屬度函數(shù)，使用遺傳算法對(duì)隸屬函數(shù)及比例因子做出優(yōu)化。以3層非線性鋼結(jié)構(gòu)地震響應(yīng)為例，分別對(duì)模糊控制算法及遺傳算法優(yōu)化后模糊控制算法進(jìn)行數(shù)值分析，結(jié)果表明：經(jīng)遺傳算法優(yōu)化后的模糊控制，進(jìn)一步降低了非線性鋼結(jié)構(gòu)的加速度和位移等響應(yīng)。

關(guān)鍵詞：鋼結(jié)構(gòu)；振動(dòng)控制；模糊控制；遺傳算法

0引言

我國(guó)是個(gè)地震多發(fā)國(guó)家，如何減少地震對(duì)建筑結(jié)構(gòu)的破壞是一個(gè)重要的研究課題。對(duì)結(jié)構(gòu)進(jìn)行振動(dòng)控制研究是國(guó)內(nèi)外的研究熱點(diǎn)。

利用壓電材料制作壓電變摩擦阻尼控制裝置，結(jié)合合理的控制算法，可以有效地降低建筑結(jié)構(gòu)在地震作用下的響應(yīng)，國(guó)內(nèi)外的很多學(xué)者進(jìn)行了深入研究。Kamada等[1]應(yīng)用多層式壓電陶瓷驅(qū)動(dòng)器對(duì)4層鋼框架模型進(jìn)行控制；楊飏等[2]提出壓電摩擦阻尼器，對(duì)兩自由度結(jié)構(gòu)進(jìn)行了半主動(dòng)控制研究；瞿偉廉等[3]設(shè)計(jì)了壓電材料智能摩擦阻尼器，對(duì)高聳塔結(jié)構(gòu)風(fēng)振進(jìn)行了LQR控制研究；張永兵等[4-6]設(shè)計(jì)了一款新型壓電變摩擦阻尼器，采用模糊控制、變?cè)鲆婺：刂坪妥詤f(xié)調(diào)模糊控制等控制算法對(duì)3層及20層鋼結(jié)構(gòu)的非線性減振控制進(jìn)行了研究。

由于模糊系統(tǒng)較依賴于專家經(jīng)驗(yàn)，可以應(yīng)用遺傳算法來(lái)優(yōu)化模糊控制，改善效果。Shook等[7]利用遺傳算法對(duì)3層鋼結(jié)構(gòu)的模糊控制器進(jìn)行了優(yōu)化，控制系統(tǒng)的效果有了顯著提升；汪權(quán)等[8]采用遺傳算法優(yōu)化模糊規(guī)則庫(kù)，對(duì)3層和6層框架結(jié)構(gòu)進(jìn)行了數(shù)值仿真分析；鄭偉等[9]采用遺傳算法優(yōu)化模糊規(guī)則庫(kù)，對(duì)高層建筑風(fēng)振進(jìn)行了仿真分析。

本文選擇壓電變摩擦阻尼器作為作動(dòng)器，通過(guò)遺傳算法對(duì)所設(shè)計(jì)的模糊控制算法中的比例因子、模糊控制的隸屬函數(shù)進(jìn)行了優(yōu)化，實(shí)現(xiàn)對(duì)地震作用下的3層非線性鋼結(jié)構(gòu)的減振控制，有效降低結(jié)構(gòu)的響應(yīng)。

1模糊控制

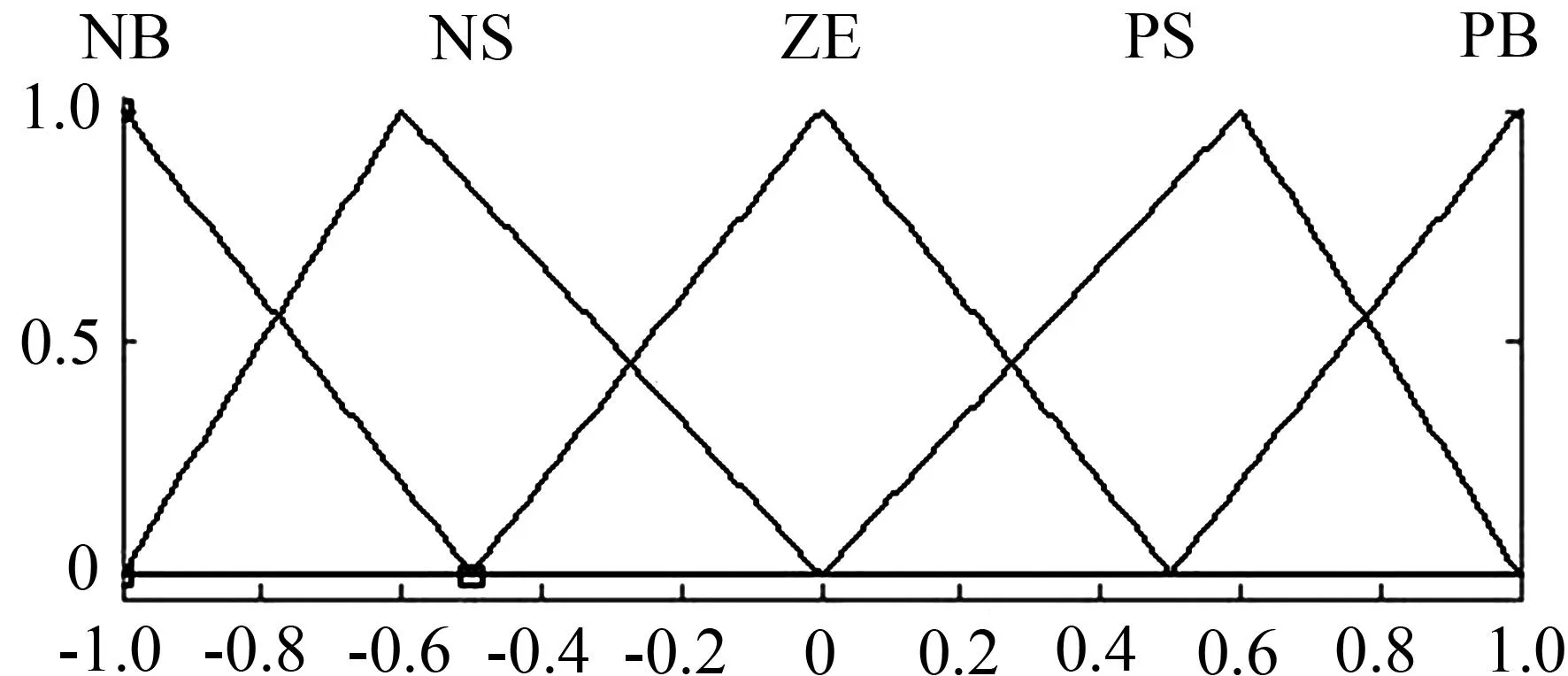
本文選擇文獻(xiàn)[4]制作的壓電變摩擦阻尼器作為半主動(dòng)控制器。在模糊邏輯控制器的模型中，采用雙輸入單輸出的模糊控制器。選取了結(jié)構(gòu)的層間位移的絕對(duì)值、結(jié)構(gòu)的層間速度的絕對(duì)值作為模糊控制器的輸入變量，輸出變量為作用電壓。在隸屬度函數(shù)的選用上，使用三角形函數(shù)作為輸入、輸出語(yǔ)言變量的隸屬度函數(shù)，各個(gè)輸入變量和輸出變量定義為五個(gè)量級(jí)：PS(正小)，NS(負(fù)小)，ZE(零)，NB(負(fù)大)，PB(正大)。結(jié)構(gòu)層間位移絕對(duì)值的隸屬度函數(shù)和層間速度絕對(duì)值隸屬度函數(shù)分別見(jiàn)圖1和圖2，輸出電壓的隸屬度函數(shù)見(jiàn)圖3，模糊控制規(guī)則見(jiàn)表1。本模型中利用的模糊推理算法為Mamdani推理法，解模糊法選用加權(quán)平均法。增加位移量化因子和速度量化因子兩個(gè)參數(shù)，位移量化因子將輸入的每一樓層的最大位移的絕對(duì)值變換到輸入的模糊論域中，速度量化因子同理。電壓比例因子用于將模糊控制器的輸出量轉(zhuǎn)化為作用電壓。本文中，位移量化因子選用各樓層位移絕對(duì)值的最大值的倒數(shù)，速度量化因子選用各樓層速度絕對(duì)值的最大值的倒數(shù)，根據(jù)以往經(jīng)驗(yàn)，可以達(dá)到比較好的效果[4],電壓比例因子選用100。

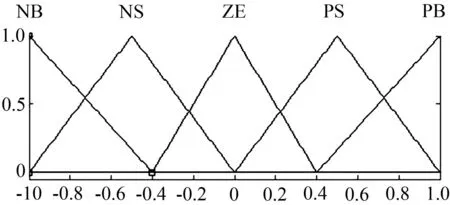
圖1輸入位移的隸屬函數(shù)

Fig.1Membership functions of displacement

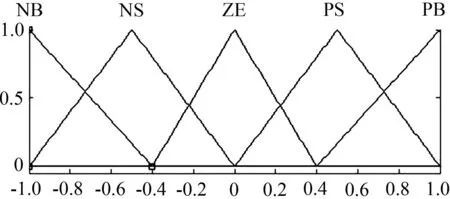
圖2輸入速度的隸屬函數(shù)

Fig.2Membership functions of velocity

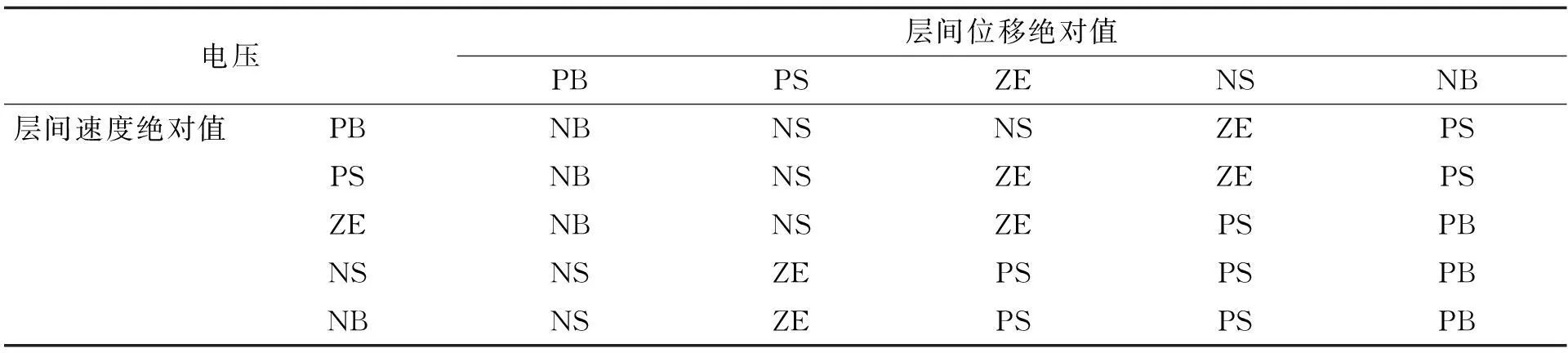
電壓層間位移絕對(duì)值PBPSZENSNB層間速度絕對(duì)值PBNBNSNSZEPSPSNBNSZEZEPSZENBNSZEPSPBNSNSZEPSPSPBNBNSZEPSPSPB

2遺傳算法優(yōu)化模糊控制

2.1編碼

本文利用遺傳算法對(duì)所設(shè)計(jì)的模糊控制算法中的電壓比例因子、模糊控制的隸屬函數(shù)進(jìn)行了優(yōu)化改進(jìn)，使用浮點(diǎn)數(shù)編碼方法。編碼被串接成一個(gè)染色體組，遺傳算法程序?qū)?huì)不斷優(yōu)化這個(gè)染色體組，以期得到更好的數(shù)據(jù)，使用變量m1～m8來(lái)描述位移、速度、電壓三個(gè)隸屬度函數(shù)中的變量，如圖4和圖5所示。

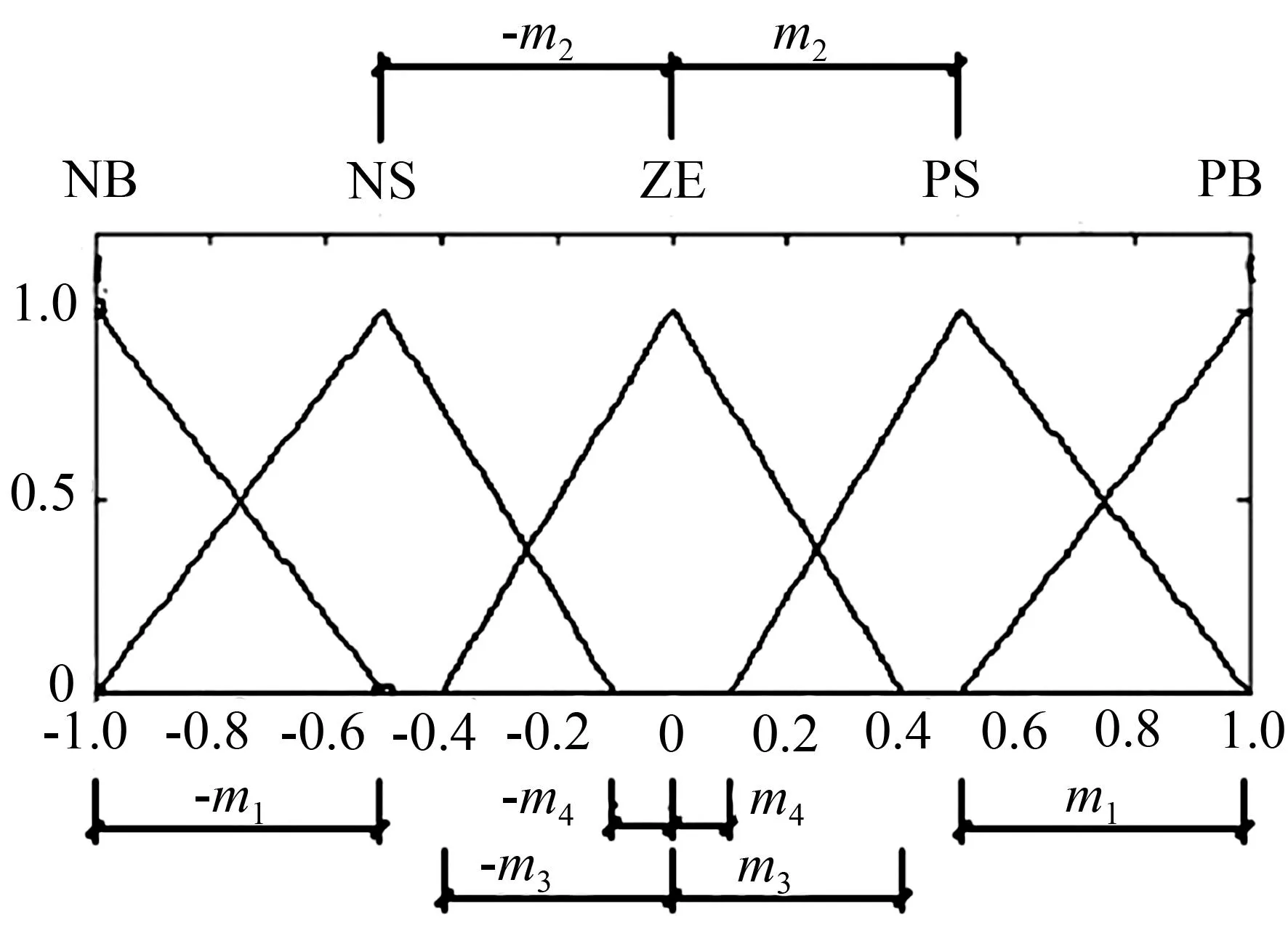
圖4優(yōu)化設(shè)計(jì)速度和位移的隸屬度函數(shù)

Fig.4Ga-optimizing membership functions of

velocity and displacement

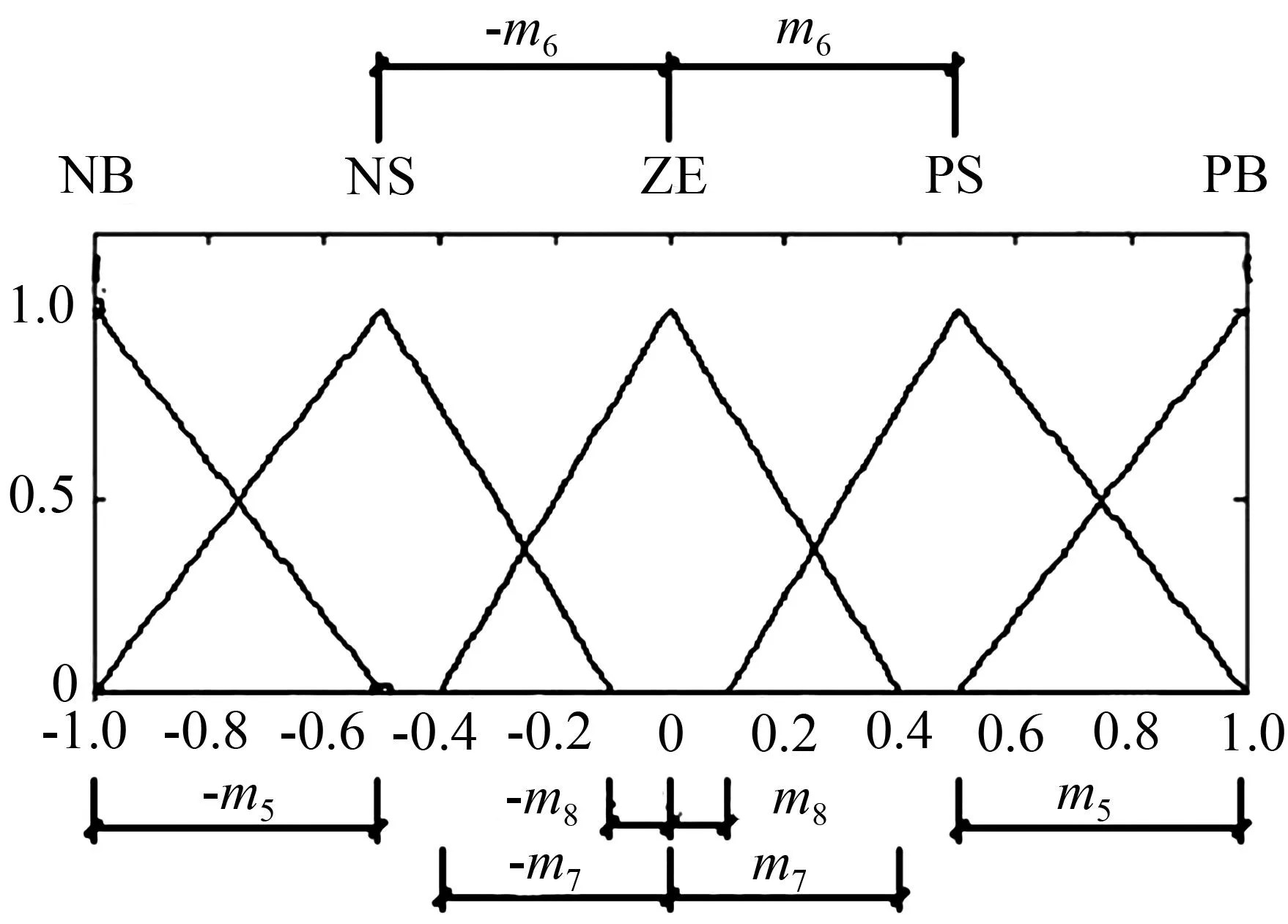
圖5優(yōu)化設(shè)計(jì)輸出電壓的隸屬度函數(shù)

Fig.5Ga-optimizing membership

functions of voltage

為了便于運(yùn)用遺傳算法進(jìn)行優(yōu)化，對(duì)控制器的電壓比例因子進(jìn)行編碼，用變量K1，K2和K3分別表示第1層、第2層和第3層的電壓比例因子。

2.2設(shè)置初始種群

經(jīng)過(guò)編碼后，初始種群的設(shè)置參數(shù)決定了遺傳算法的復(fù)雜性[10]。本文首先確定了浮點(diǎn)數(shù)編碼部分的待優(yōu)化變量有11個(gè)。為了減小遺傳算法搜索空間和縮小范圍，盡快的確定最優(yōu)解，遺傳算法的定義需要對(duì)變量設(shè)定邊界條件，如表2所示。

表2　初始種群邊界條件

2.3適應(yīng)度函數(shù)設(shè)計(jì)

適應(yīng)度函數(shù)影響遺傳算法的使用功能，是下一步運(yùn)算的基礎(chǔ)[11]。本文優(yōu)化的目的是使結(jié)構(gòu)在地震作用下的位移響應(yīng)等指標(biāo)保持在合理范圍內(nèi)，以結(jié)構(gòu)的最大位移作為評(píng)價(jià)控制器的性能指標(biāo)，最大位移可能出現(xiàn)在任何一層，用式(1)來(lái)表示：

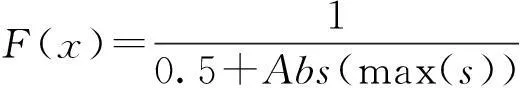
(1)

式中s是地震作用下鋼框架某時(shí)刻的最大位移。

2.4選擇運(yùn)算

選擇算子是遺傳算法的關(guān)鍵[12]。本文應(yīng)用的選擇算子是輪盤賭選擇，個(gè)體的適應(yīng)度越高，選入的幾率也就越大，具體可用式(2)表示:

(2)

其中：n代表了群體的總數(shù)，fi為群體中i個(gè)體的適應(yīng)度，Pi代表i個(gè)體被選擇的概率。

2.5交叉、變異運(yùn)算

遺傳算法的交叉運(yùn)算就是匹配兩個(gè)相應(yīng)的染色體且進(jìn)行基因交換，繁衍出下一代個(gè)體。染色體是經(jīng)過(guò)選擇操作篩選過(guò)的高適應(yīng)度染色體。本文采用對(duì)位交叉算法。交叉運(yùn)算能繁衍出新的基因型和不同于前一代的個(gè)體。

之前敘述的選擇運(yùn)算和交叉運(yùn)算主要是說(shuō)繼承基因的問(wèn)題。變異運(yùn)算是在適應(yīng)度高的基因的后代里改變少量基因，產(chǎn)生少數(shù)異種。本文的變異運(yùn)算使用自適應(yīng)變異方法。隨著進(jìn)化進(jìn)程的不斷進(jìn)行，使變異率隨之減小，這能保證變異運(yùn)算不會(huì)太快收斂。在實(shí)際模擬過(guò)程優(yōu)化模糊控制中的比例因子和隸屬函數(shù)中，變異很容易產(chǎn)生波動(dòng)，使得數(shù)據(jù)不穩(wěn)定或者朝著錯(cuò)誤的方向收斂。可以用式(3)來(lái)確定變異率，保持優(yōu)良個(gè)體，防止其被改變。

Pn=0.01-Sn×0.01/S,

(3)

其中：Sn代表當(dāng)前進(jìn)化代數(shù)，S代表進(jìn)化總代數(shù)，Pn是當(dāng)前的變異率。

3算例

3.1仿真模型

本算例所使用模型是3層非線性鋼框架結(jié)構(gòu)[13]。3層非線性鋼框架結(jié)構(gòu)中，每一層安裝一個(gè)壓電變摩擦阻尼器。對(duì)遺傳算法中各參數(shù)的初始設(shè)置:初始種群個(gè)數(shù)為30個(gè)，種群迭代代數(shù)為75代，選擇概率為75%，交叉概率為45%，變異概率為10%。

3.2仿真結(jié)果

經(jīng)過(guò)Matlab模擬仿真，模糊控制系統(tǒng)中第1、2、3層的電壓比例因子K1、K2、K3優(yōu)化后分別由100變?yōu)?31、140、127。利用遺傳算法優(yōu)化結(jié)果導(dǎo)出的模糊控制的隸屬函數(shù)如圖6，圖7和圖8所示。將遺傳算法優(yōu)化所得的隸屬函數(shù)應(yīng)用于模糊控制系統(tǒng)中，結(jié)構(gòu)在EI Centro波作用下頂層的位移響應(yīng)及速度響應(yīng)分別如圖9和圖10所示，結(jié)構(gòu)的峰值位移如表3所示。

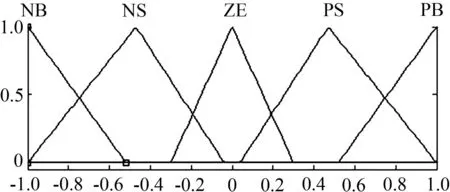
圖6遺傳算法優(yōu)化之后的位移隸屬函數(shù)

Fig.6Membership functions for displacementafter

genetic algorithm optimization

圖7遺傳算法優(yōu)化之后的速度隸屬函數(shù)

Fig.7Membership functions for velocity after

genetic algorithm optimization

圖8　遺傳算法優(yōu)化之后的電壓隸屬函數(shù)

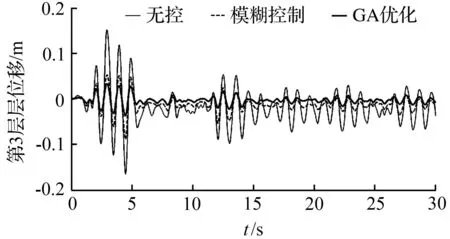
圖9　EI波作用下3層位移時(shí)程曲線

1.控制率=(無(wú)控結(jié)構(gòu)響應(yīng)峰值-受控結(jié)構(gòu)響應(yīng)峰值)/無(wú)控結(jié)構(gòu)響應(yīng)峰值。

從圖9和圖10可知，在EI波的作用下，鋼結(jié)構(gòu)3層的峰值加速度，不受控制時(shí)為7.397 m/s2，使用模糊控制時(shí)時(shí)為3.207 m/s2，使用遺傳算法優(yōu)化的模糊控制時(shí)為1.822 m/s2，優(yōu)化后的模糊控制控制率為75.4%；鋼結(jié)構(gòu)3層的峰值位移，無(wú)控時(shí)為0.164 5 m，使用模糊控制時(shí)為0.058 1 m，使用遺傳算法優(yōu)化的模糊控制時(shí)為0.034 2 m，優(yōu)化后的模糊控制控制率為79.2%。說(shuō)明經(jīng)過(guò)遺傳算法優(yōu)化后的模糊控制系統(tǒng)，其參數(shù)更加合理，控制效果也更加明顯。

結(jié)構(gòu)在Hachinohe波作用下頂層的位移響應(yīng)及速度響應(yīng)分別如圖11和圖12所示，結(jié)構(gòu)的峰值位移如表4所示。

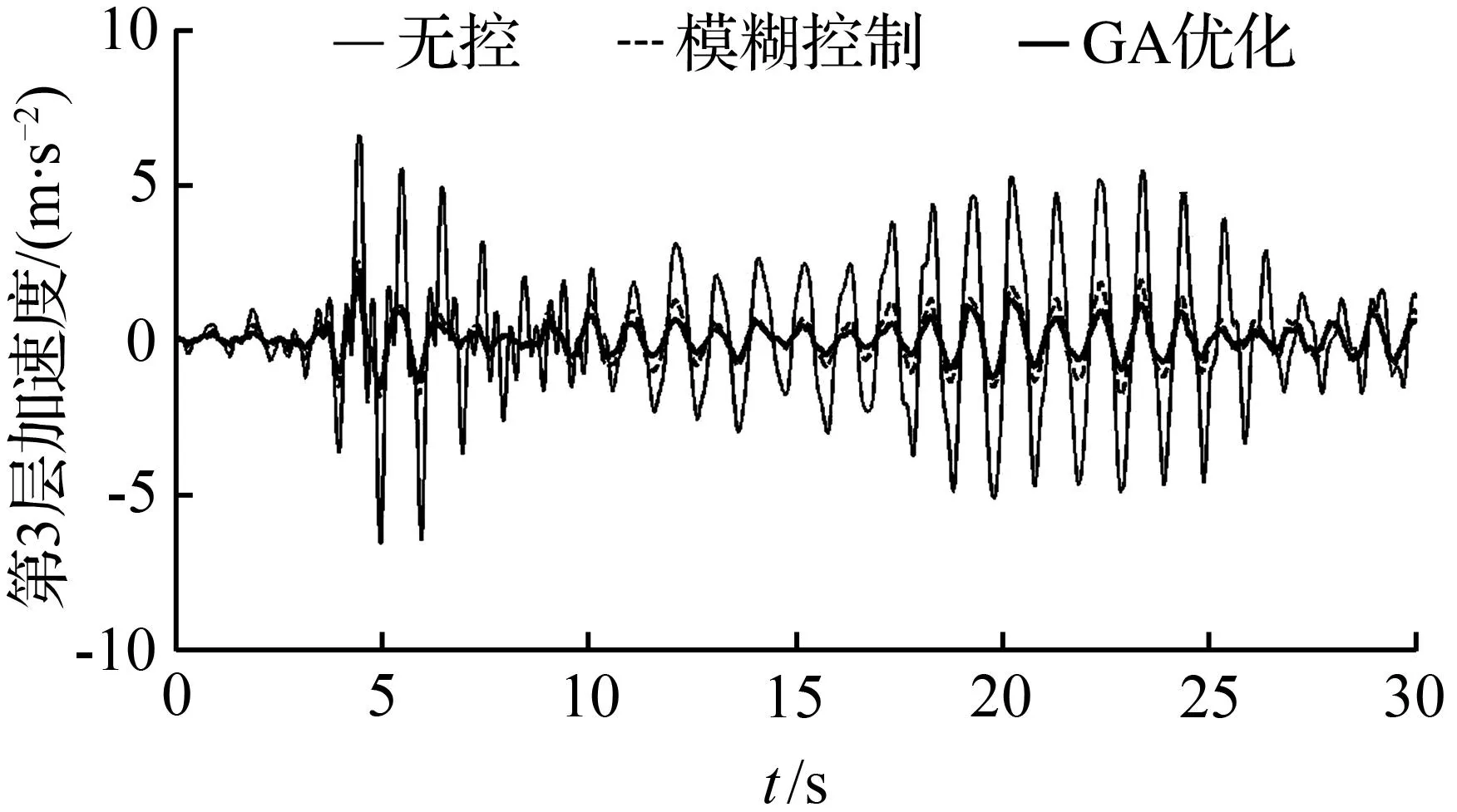
圖11　Hachinohe波作用下3層位移時(shí)程

從圖11和圖12可以看出，在Hachiohe波的作用下，鋼結(jié)構(gòu)3層的峰值加速度，不受控制時(shí)為6.606 m/s2，模糊控制時(shí)為2.781 m/s2，使用遺傳算法優(yōu)化的模糊控制時(shí)為2.249 m/s2，優(yōu)化后的模糊控制控制率能達(dá)到66.0%；鋼結(jié)構(gòu)3層的峰值位移，無(wú)控時(shí)為0.153 6 m，模糊控制時(shí)為0.053 1 m，使用遺傳算法優(yōu)化的模糊控制時(shí)為0.040 1 m，優(yōu)化后的模糊控制控制率能達(dá)到73.9%。同EI波的作用下情況相似，經(jīng)過(guò)優(yōu)化后，模糊控制更合理，控制效果也更好。

4結(jié)語(yǔ)

本文選擇壓電變摩擦阻尼器作為作動(dòng)器，通過(guò)遺傳算法對(duì)所設(shè)計(jì)的模糊控制算法中的比例因子、模糊控制的隸屬函數(shù)進(jìn)行了優(yōu)化，并將遺傳算法優(yōu)化后的模糊控制應(yīng)用于設(shè)置了壓電變摩擦阻尼器的3層非線性鋼框架結(jié)構(gòu)的振動(dòng)控制中。從算例中得出的結(jié)果中，經(jīng)過(guò)遺傳算法優(yōu)化后的模糊控制，相對(duì)于研究人員憑經(jīng)驗(yàn)來(lái)設(shè)計(jì)參數(shù)的模糊控制，鋼結(jié)構(gòu)的加速度和位移響應(yīng)有了明顯的改善，取得了很好的減振的效果。

參考文獻(xiàn)：

[1]KAMADA T, FUJITA T, HATAYAMA T, et al. Active vibration of frame structures of shear and bending type with smart structure using piezoelectric actuator[J]. Smart Structures and Materials, 1997, 3041(1): 75-86.

[2]楊飏，歐進(jìn)萍.壓電變摩擦阻尼器減振結(jié)構(gòu)的數(shù)值分析[J].振動(dòng)與沖擊，2005，24(6)：1-4.

[3]瞿偉廉，陳朝暉，徐幼麟.壓電材料智能磨擦阻尼器對(duì)高聳鋼塔結(jié)構(gòu)風(fēng)振反應(yīng)的半主動(dòng)控制[J].地震工程與工程振動(dòng)，2000，20(1)：94-99.

[4]張永兵，秦榮，李雙蓓.壓電變摩擦阻尼器對(duì)高層建筑非線性地震反應(yīng)的模糊控制算法[J].振動(dòng)與沖擊，2008，27(11)：142-146.

[5]張永兵，秦榮，李雙蓓.3層鋼結(jié)構(gòu)非線性地震反應(yīng)的變?cè)鲆婺：刂芠J].振動(dòng)與沖擊，2008，27(10)：106-111.

[6]張永兵，李雙蓓，吳炯，等.壓電變摩擦阻尼結(jié)構(gòu)的模糊控制[J].廣西大學(xué)學(xué)報(bào)(自然科學(xué)版)，2009，34(1)：17-21.

[7]SHOOK D A, ROSCHKE P N, LIN P Y,et al. GA-optimized fuzzy logic control of a large-scale building for seismic loads [J]. Engineering Structure,2008, 30(2): 436-449.

[8]汪權(quán)，王建國(guó).建筑結(jié)構(gòu)地震響應(yīng)半主動(dòng)控制的遺傳—模糊算法[J].地震工程與工程震動(dòng)，2010，30(6)：127-133.

[9]鄭偉，閻石.基于遺傳算法優(yōu)化的高層建筑風(fēng)振模糊控制[J].地震工程與工程震動(dòng)，2009，29(4)：178-182.

[10]喬孟麗，張景元，溫瑩瑩.一種基于遺傳算法的模糊控制規(guī)則的優(yōu)化方法[J].計(jì)算機(jī)測(cè)量與控制，2006，14(10)：1349-1351.

[11]宋雨，陳衛(wèi)東，張錦.高速列車半主動(dòng)懸掛系統(tǒng)遺傳優(yōu)化模糊控制[J].噪聲與振動(dòng)控制，2012，32(6)：158-164.

[12]郭曉品.基于遺傳算法的智能桁架結(jié)構(gòu)模糊控制研究[D].邯鄲：河北工程大學(xué)，2011.

[13]OHTORI Y, CHRISTENSON R E, ASCE A M, et al. Benchmark control problems for seismically excited nonlinear buildings[J]. Journal of Engineering Mechanics, 2004, 130(4): 366-385.

(責(zé)任編輯唐漢民梁碧芬)

Genetic algorithm optimized fuzzy control of nonlinear steel structure

ZHANG Yong-bing, LIANG Xing-yun, TANG Ying, CHEN Li-xing

(College of Civil and Architectural Engineering, Guangxi University, Nanning 530004, China)

Abstract：Membership functions and scaling factors of fuzzy logic controller wereoptimized by the genetic algorithm.The piezoelectric friction damper wasregarded as the control device, and an optimized fuzzy control algorithm was proposed to reduce the seismic response of nonlinear steel structures. Fuzzy controller based on dual inputs and single output, absolute value of interstory drifts and interstory velocities wereselected as input variables;voltages wereselected as output variables;triangular shapes wereselected as input and output variables of membership functions.Membership functions and scaling factors of fuzzy logic controller wereoptimized by thegenetic algorithm. A 3-story nonlinear steel structure wasanalyzed to simulate numerically the seismic responses under an optimized fuzzy logic controller.Numerical analysis results show that the fuzzy logic controllers optimized by genetic algorithm are effective in reduction of both acceleration and displacement responses of nonlinear steel structures.

Key words:steel structure; vibration control; fuzzy control; genetic algorithm

中圖分類號(hào):P315.966; TU352.11

文獻(xiàn)標(biāo)識(shí)碼:A

文章編號(hào)：1001-7445(2016)01-0107-07

doi:10.13624/j.cnki.issn.1001-7445.2016.0107

通訊作者：張永兵(1979—)，男，河南襄城人，廣西大學(xué)副研究員，博士;E-mail:zhangyongbing@foxmail.com。

基金項(xiàng)目：廣西自然科學(xué)基金資助項(xiàng)目(2013GXNSFBA019236)；廣西科技攻關(guān)計(jì)劃項(xiàng)目(桂科攻12426001-5)；“廣西防災(zāi)減災(zāi)與工程安全重點(diǎn)實(shí)驗(yàn)室”系統(tǒng)性研究項(xiàng)目(2013ZDX10)；廣西大學(xué)科研項(xiàng)目(土科基-2012-03)

收稿日期：2015-11-12；

修訂日期：2015-12-26

引文格式：張永兵，梁星云，唐瀅,等.遺傳算法優(yōu)化的非線性鋼結(jié)構(gòu)模糊控制研究[J].廣西大學(xué)學(xué)報(bào)(自然科學(xué)版)，2016，41(1)：107-113.