模糊控制器設計及其優化研究

曾春華，劉雪梅

（同濟大學機械與能源工程學院，浙江 寧波 315021）

模糊控制器設計及其優化研究

曾春華，劉雪梅

（同濟大學機械與能源工程學院，浙江 寧波 315021）

模糊控制器中的量化因子和比例因子會改變模糊控制器的輸出特性，對模糊控制器的輸出性能有很大的影響。但是模糊控制器一旦設計完畢，模糊控制器的量化因子和比例因子就被固定，無法根據實際運行結果來進行參數的調整。本文在完成模糊控制算法設計的基礎上，采用PSO算法對運行過程中的模糊控制參數進行調整，并通過與傳統模糊控制器的對比，得出本文所研究的基于PSO算法的模糊控制器的收斂速度更快，可以獲得更好的控制效果。

模糊控制器；粒子群算法；參數調整

與建立在精確數學模型基礎上的現代控制理論系統相比，工業生產中的控制系統的被控對象更加復雜，而且不確定因素也更多。模糊控制器是一種非線性控制器，其模糊控制規則和隸屬度函數的確定困難，目前還沒有有效的模糊控制器設計和調整方法。本文擬采用粒子群算法對模糊控制器參數調節優化進行研究。

1 基于PSO的模糊控制算法設計

1.1 算法設計思路

針對模糊控制器設計完成之后，難根據實際情況調節控制的問題，本文主要采用粒子群算法與模糊控制器的結合，來實現模糊控制器中量化因子Ke、Kec和比例因子Ku三個參數的調節，以取得更好的控制修改。

粒子群優化算法（Particle Swarm Optimization，PSO）是Kennedy在鳥類捕食活動規律的啟發下所提出來的一種仿生物智慧概念算法。PSO算法將一組隨機解作為系統的初始解，通過不斷的迭代來獲得問題的最優解或較優解。與同樣采用迭代的遺傳算法相比，PSO算法不需要很多參數的調整，其算法及其實現更加簡單，是一個很好的多重最優解問題解決方法。

1.2 參數調整原則

模糊控制器中作為輸入變量的量化因子具有量化效應，而作為輸出的比例因子只有比例作用。模糊控制器中量化因子Ke、Kec和比例因子Ku的大小對模糊控制系統的動態性能有很大的影響，其影響具體表現在如下幾個方面。

（1）當Ke較大時，系統超調較大，導致控制系統的過渡過程較長。

（2）當Kec較大時，會減少系統的超調量，降低系統的響應速度。

（3）uK是模糊控制器的總增益，其選擇影響控制器的輸出，如果參數uK選擇過小，那么會增加系統的動態響應過程，而如果參數uK選擇過大，則有可能會導致系統振蕩，長時間無法收斂。

1.3 目標函數選擇

快速性、準確性和穩定性是衡量一個控制系統的三個指標，目前常用的模糊控制器性能指標只含有時間和誤差兩個變量，雖然這些指標的量獲取容易，但是誤差總是以絕對值的形式出現，無法表現出模糊控制器系統的正誤差和負誤差。

ITAE（Integral of Time-weighted Absolute value of the Error，時間加權絕對誤差值積分）性能判定準則可以讓控制系統具有快速響應特性，因此在本文的研究中，將選擇ITAE準則作為判斷模糊控制系統性能優劣的目標函數，同時根據模糊控制系統的特點，還應該在目標函數中加入系統超調量約束，最終確定的系統參數優化目標函數設計如公式（1）所示。

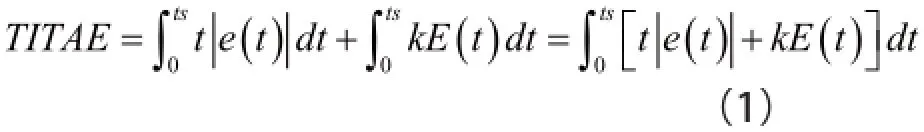
1.4 PSO參數調節算法

在本文中使用SIMULINK仿真軟件，對非線性動態系統進行仿真。為了優化設計，先構建動態系統，然后得到動態仿真結果。使用PSO算法實現的模糊控制優化流程如圖1所示。

如圖1所示，使用PSO粒子群算法，確定模糊控制器的各參數的值，以達到模糊控制器超調最小，提高模糊控制收斂的目的。

2 基于PSO的模糊控制器仿真

2.1 仿真結構設計

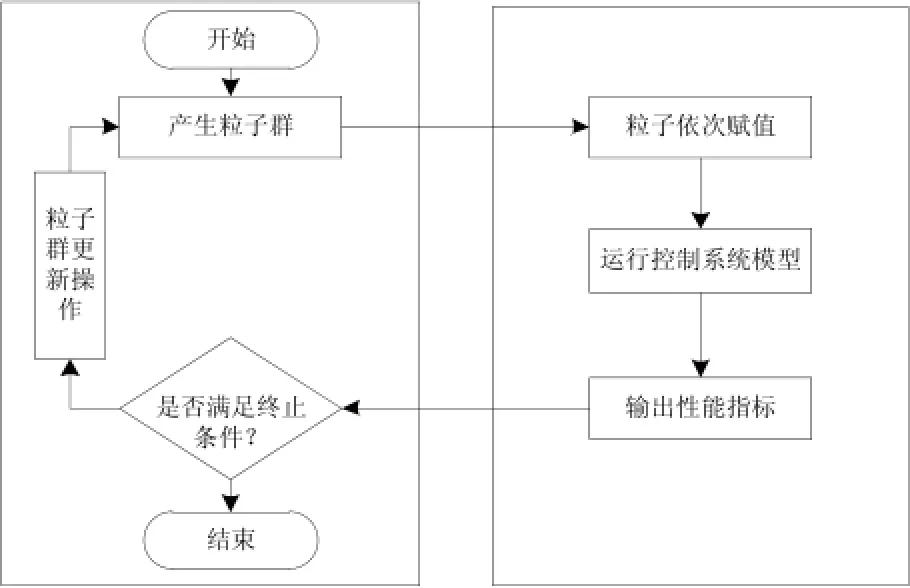
圖1 PSO參數優化流程圖

在對基于PSO的模糊控制器仿真過程中，首先確定控制器的Kp（比例）、Ki（積分）、Kd（微分）與誤差之間的模糊關系，并根據模糊控制規則對控制器的三個參數進行調整，提高控制對象的性能。通過對模糊控制器的分析，將誤差作為模糊控制器的輸入，將控制器的Kp、Ki、Kd三個參數作為輸出來設計如圖2所示的仿真圖。

圖2 模糊控制器仿真圖

確定模糊子集為：｛NB, NM, NS, ZO, PS, PM, PB｝，各變量的模糊論域設計為：Kp∈［-0.3,0.3］，Ki∈［-0.06,0.06］，Kd∈［-3,3］。

2.2 仿真實驗分析

基于前面所研究設計的仿真結構和模糊規則，以如式（2）所示的二階傳遞函數的階躍響應來對本文基于PSO的模糊控制器和傳統模糊控制器進行對比，并對仿真結果進行分析。

設計采樣的時間為1ms，其中粒子群算法參數設定為：每個粒子維度設定為3，粒子種群數設定為100，最大迭代數設計為100，c1=c2=2.05。

兩種模糊控制器作用下的階躍響應曲線仿真結果如圖3所示。

圖3 兩種模糊控制器作用下的階躍響應曲線仿真結果

如圖3所示，基于PSO算法的模糊控制器的超調量更少，超調時間更短，表明基于PSO算法的模糊控制器的穩定性更好，被控制對象能夠更加快速的達到穩定狀態。

3 結語

模糊控制不需要建立精確的數學控制模型，可以很好的解決系統的時滯性和不確定性，模糊控制已經成為了智能控制的重要研究方向。在模糊控制器的設計過程中，其隸屬函數往往是通過經驗或專家知識獲得，一旦模糊控制器確定，其隸屬函數形狀也確定了，因此無法對隸屬函數是否適應狀態變量進行判斷。

本文基于PSO算法，對模糊控制器進行改進和優化，實驗仿真結果表明，本文所設計的基于PSO算法的模糊控制器的響應速度快，超調小，能夠更快的達到穩定狀態。

[1]陳婷婷，李鳳.基于粒子群優化訓練的模糊控制數學建模方法[J].科技通報，2016,08(31).

[2]陳曄，李生剛，劉恒.基于自適應模糊控制的分數階混沌系統同步[J].物理學報，2016,09(8).

[3]錢浩.淺談模糊控制[J].黑龍江科技信息，2015,03(25).

[4]陳摯.模糊控制理論的應用分析[J].科技風，2015,04(25).

[5]殷業.模糊控制的本質[J].前沿科學，2015,03(28).

TP273.4

A

1671-0711（2016）12（下）-0150-02