基于模塊度優(yōu)化的加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法分析
楊春明 王玉金
(西南科技大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院 四川綿陽(yáng) 621010)
基于模塊度優(yōu)化的加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法分析
楊春明 王玉金
(西南科技大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院 四川綿陽(yáng) 621010)
社團(tuán)結(jié)構(gòu)是復(fù)雜網(wǎng)絡(luò)的一種重要拓?fù)浣Y(jié)構(gòu)。針對(duì)加權(quán)復(fù)雜網(wǎng)絡(luò)中的社團(tuán)發(fā)現(xiàn)問(wèn)題,在8個(gè)不同領(lǐng)域、不同規(guī)模的真實(shí)數(shù)據(jù)集上,從模塊度、強(qiáng)/弱社團(tuán)、聚集系數(shù)3個(gè)評(píng)估指標(biāo)分析了基于模塊度優(yōu)化的GN算法、FN算法、CNM算法和BGLL算法在加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)的效果。研究結(jié)果表明,上述3個(gè)評(píng)估指標(biāo)在加權(quán)復(fù)雜網(wǎng)絡(luò)上的劃分結(jié)果不能始終保持一致,基于優(yōu)化模塊度的算法更傾向于找到復(fù)雜網(wǎng)絡(luò)中比較粗糙的社團(tuán)結(jié)構(gòu),而不是精準(zhǔn)的社團(tuán)結(jié)構(gòu),其算法的泛化能力有待加強(qiáng)。
加權(quán)復(fù)雜網(wǎng)絡(luò) 社團(tuán)發(fā)現(xiàn) 模塊度 聚集系數(shù)
現(xiàn)實(shí)中大量的復(fù)雜系統(tǒng)通常可用網(wǎng)絡(luò)來(lái)描述,如互聯(lián)網(wǎng)絡(luò)、社交網(wǎng)絡(luò)、科學(xué)家合作網(wǎng)絡(luò)、病毒傳播網(wǎng)絡(luò)等,這些抽象出來(lái)的復(fù)雜網(wǎng)絡(luò)通常具有小世界[1]及無(wú)標(biāo)度特性[2]。復(fù)雜網(wǎng)絡(luò)的一個(gè)重要結(jié)構(gòu)特征是網(wǎng)絡(luò)的社團(tuán)(community)結(jié)構(gòu)[3],又稱(chēng)為群(group)或簇(cluster),社團(tuán)內(nèi)部節(jié)點(diǎn)連接緊密,社團(tuán)間連接相對(duì)稀疏,社團(tuán)內(nèi)部節(jié)點(diǎn)都具有比較相近的屬性[4]。
復(fù)雜網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)研究主要用于理解網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)、挖掘網(wǎng)絡(luò)的潛在意義及預(yù)測(cè)網(wǎng)絡(luò)行為等。對(duì)無(wú)權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn),主要有譜聚類(lèi)方法[5]、KL(Kernighan-Lin)算法[6]、GN(Girvon-Newman)算法、FN算法[7]、CNM算法[8]、BGLL算法[9]等。
相對(duì)與無(wú)權(quán)網(wǎng)絡(luò),有權(quán)網(wǎng)絡(luò)中包含了更多的網(wǎng)絡(luò)信息,更能反映實(shí)際情況。如論文合作者網(wǎng)絡(luò)中作者共同發(fā)表論文的數(shù)量反映了作者之前的緊密程度;人與人接觸的頻度越高病毒在兩者間傳播的可能性越大。網(wǎng)絡(luò)中邊的權(quán)值反映了節(jié)點(diǎn)間連接的強(qiáng)度,在社團(tuán)結(jié)構(gòu)中,社團(tuán)內(nèi)邊的平均權(quán)值更大,連接緊密,而社團(tuán)間連邊的平均權(quán)值較小,連接相對(duì)稀疏。
加權(quán)復(fù)雜網(wǎng)絡(luò)的復(fù)雜性遠(yuǎn)高于無(wú)權(quán)網(wǎng)絡(luò),社團(tuán)劃分結(jié)果的評(píng)價(jià)指標(biāo)也有了較大變化。目前的研究大多針對(duì)無(wú)權(quán)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)[10],已有一些研究進(jìn)行了單一算法對(duì)特定數(shù)據(jù)集的分析[11]、多種加權(quán)復(fù)雜網(wǎng)絡(luò)算法的綜述[3]以及在多個(gè)指標(biāo)下利用模擬數(shù)據(jù)和小規(guī)模真實(shí)數(shù)據(jù)的對(duì)比分析[12],但在較大規(guī)模的真實(shí)數(shù)據(jù)集及社團(tuán)的層次結(jié)構(gòu)特征上的加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法還缺乏較全面的實(shí)驗(yàn)比較。對(duì)此,本文在不同領(lǐng)域、不同規(guī)模大小的8個(gè)真實(shí)數(shù)據(jù)集上分析社團(tuán)評(píng)估指標(biāo)中的模塊度、強(qiáng)弱社團(tuán)及層次特征,在加權(quán)復(fù)雜網(wǎng)絡(luò)上對(duì)基于模塊度優(yōu)化的算法進(jìn)行實(shí)驗(yàn)比較分析。
1 加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法分析
目前的社團(tuán)發(fā)現(xiàn)算法主要針對(duì)無(wú)權(quán)網(wǎng)絡(luò),在加權(quán)網(wǎng)絡(luò)上,通常考慮邊的權(quán)值信息,對(duì)無(wú)權(quán)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)算法進(jìn)行改進(jìn)。常見(jiàn)的算法有基于圖分割思想的譜聚類(lèi)算法、KL算法和基于模塊度優(yōu)化的GN算法、FN算法、CNM算法、BGLL算法等。
1.1 基于圖分割的算法
譜聚類(lèi)和KL算法將社團(tuán)劃分視為圖分割問(wèn)題。譜聚類(lèi)算法[5]將圖分割問(wèn)題中求解最小“截”問(wèn)題轉(zhuǎn)化為求解帶約束的二次型優(yōu)化問(wèn)題,利用矩陣分析技術(shù)求拉普拉斯矩陣第二小特征值對(duì)應(yīng)的特征向量問(wèn)題, 從而根據(jù)特征向量將網(wǎng)絡(luò)進(jìn)行遞歸劃分。該方法需要預(yù)先知道社團(tuán)的數(shù)量,以便定義遞歸終止條件,對(duì)具有n節(jié)點(diǎn)的網(wǎng)絡(luò),該方法的時(shí)間復(fù)雜度為O(n3)。
KL算法[6]的優(yōu)化目標(biāo)是極小化簇間連接數(shù)目與簇內(nèi)連接數(shù)目之差。KL 算法在每次迭代過(guò)程中產(chǎn)生、評(píng)價(jià)、選擇候選解,直到從當(dāng)前解出發(fā)找不到更好的候選解為止。該算法的解往往是局部最優(yōu),而不是全局最優(yōu),算法對(duì)初始解非常敏感,時(shí)間復(fù)雜度是O(tn2),其中n表示網(wǎng)絡(luò)節(jié)點(diǎn)個(gè)數(shù),t表示算法停止時(shí)的迭代次數(shù)。該算法也需要預(yù)先知道網(wǎng)絡(luò)中社團(tuán)的數(shù)量。
1.2 基于模塊度優(yōu)化的算法
模塊度優(yōu)化算法是以模塊度函數(shù)(Q函數(shù))為目標(biāo)的社團(tuán)劃分方法。
GN算法[7]將社團(tuán)劃分視為分裂過(guò)程,開(kāi)始將網(wǎng)絡(luò)整體看作一個(gè)社團(tuán),通過(guò)逐步移除當(dāng)前邊介數(shù)最大的邊來(lái)劃分出獨(dú)立的子圖。該算法以模塊度作為其評(píng)價(jià)指標(biāo),即在移除邊的同時(shí)計(jì)算移除邊后網(wǎng)絡(luò)的模塊度Q值,算法執(zhí)行過(guò)程中最大模塊度Q值對(duì)應(yīng)的網(wǎng)絡(luò)劃分狀態(tài)即是最終社團(tuán)劃分結(jié)果。在加權(quán)復(fù)雜網(wǎng)絡(luò)中,邊介數(shù)定義為原始定義下的邊介數(shù)除以邊的權(quán)值所得到的值。對(duì)于有n個(gè)節(jié)點(diǎn)m條邊的加權(quán)復(fù)雜網(wǎng)絡(luò),GN算法中計(jì)算每條邊的邊介數(shù)的算法時(shí)間復(fù)雜度為O(nm),而算法總共需要進(jìn)行m次移除邊的操作,每次都需要重新計(jì)算網(wǎng)絡(luò)中每條邊的邊介數(shù),所以該算法的最終時(shí)間復(fù)雜度為O(nm2)。
FN算法[7]是對(duì)GN算法的加速,是一種凝聚算法,開(kāi)始時(shí)將每個(gè)節(jié)點(diǎn)看作一個(gè)社團(tuán),計(jì)算合并每?jī)蓚€(gè)社團(tuán)后的模塊度Q值增益,選取使Q值增益增加最多或減少最少的兩個(gè)社團(tuán)合并成一個(gè)社團(tuán),直至整個(gè)網(wǎng)絡(luò)合并為一個(gè)社團(tuán)為止。對(duì)于加權(quán)網(wǎng)絡(luò),定義向量α,其元素a=k∑jeij,即社團(tuán)i內(nèi)部節(jié)點(diǎn)與所有社團(tuán)連邊的權(quán)值之和占網(wǎng)絡(luò)所有邊權(quán)之和的比例。合并兩個(gè)社團(tuán)的模塊度Q值增益計(jì)算公式:
ΔQ=2(eij-aiaj)
對(duì)于有n個(gè)節(jié)點(diǎn)m條邊的加權(quán)復(fù)雜網(wǎng)絡(luò),F(xiàn)N算法在執(zhí)行過(guò)程中更新矩陣等數(shù)據(jù)的最壞時(shí)間復(fù)雜度為O(n)。算法每一步的最壞時(shí)間復(fù)雜度為O(n+m),最多n-1次社團(tuán)合并操作,算法的最終時(shí)間復(fù)雜度為O((n+m)n),對(duì)于稀疏矩陣為O(n2)。
CNM算法[8]是對(duì)FN算法時(shí)間復(fù)雜度的改進(jìn),通過(guò)使用堆來(lái)構(gòu)造模塊度增量矩陣從而達(dá)到快速定位當(dāng)前應(yīng)合并的兩個(gè)社團(tuán)的目的。該算法執(zhí)行過(guò)程依然是一個(gè)聚集過(guò)程,初始時(shí)將每個(gè)節(jié)點(diǎn)看作一個(gè)社團(tuán),同樣以模塊度Q值作為評(píng)價(jià)指標(biāo)。對(duì)于有n個(gè)點(diǎn)m條邊的加權(quán)復(fù)雜網(wǎng)絡(luò)。由于CNM算法采用了堆來(lái)構(gòu)造模塊度增量矩陣,所以在每次更新矩陣時(shí)復(fù)雜度為O(logn),而在每次決策合并的兩個(gè)社團(tuán)時(shí)只需要常數(shù)時(shí)間O(1),算法最多執(zhí)行n-1次社團(tuán)合并操作,最終算法針對(duì)稀疏網(wǎng)絡(luò)的時(shí)間復(fù)雜度為O(mlogn)。
BGLL[9]是一種重疊社團(tuán)發(fā)現(xiàn)算法,每次迭代分為兩個(gè)階段。第一階段將每個(gè)節(jié)點(diǎn)看作單獨(dú)的社團(tuán),考慮將每個(gè)節(jié)點(diǎn)i移除出其當(dāng)前所在的社團(tuán),移入其鄰居節(jié)點(diǎn)j所在的社團(tuán)C。第二個(gè)階段將根據(jù)第一個(gè)階段的結(jié)果構(gòu)造一個(gè)新的網(wǎng)絡(luò),即將第一步中劃分出的各社團(tuán)各自看作一個(gè)節(jié)點(diǎn),社團(tuán)內(nèi)部邊的權(quán)重之和作為新節(jié)點(diǎn)的自環(huán)權(quán)重,相應(yīng)的社團(tuán)與其他社團(tuán)所有連邊的權(quán)重之和作為新節(jié)點(diǎn)之間邊的權(quán)重值。
BGLL算法提出的模塊度增益計(jì)算公式簡(jiǎn)易,以及算法執(zhí)行過(guò)程中社團(tuán)數(shù)目在前幾次迭代中急劇減少,在針對(duì)稀疏網(wǎng)絡(luò)時(shí)有接近線性的時(shí)間復(fù)雜度。執(zhí)行速度快是BGLL算法的一個(gè)非常大的優(yōu)勢(shì),使BGLL算法能在較短的時(shí)間消耗下處理上千萬(wàn)甚至上億節(jié)點(diǎn)的復(fù)雜網(wǎng)絡(luò),同時(shí)該算法還能保持良好的社團(tuán)劃分效果。
綜上所述,上述6種算法的特點(diǎn)如表1所示。

表1 算法特點(diǎn)比較Table 1 Algorithm features
2 加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)劃分評(píng)估指標(biāo)
復(fù)雜網(wǎng)絡(luò)的社團(tuán)劃分需要有效的評(píng)價(jià)指標(biāo)對(duì)社團(tuán)劃分的過(guò)程進(jìn)行指導(dǎo),并對(duì)社團(tuán)劃分結(jié)果的效果進(jìn)行衡量。對(duì)無(wú)權(quán)復(fù)雜網(wǎng)絡(luò),常見(jiàn)的評(píng)估指標(biāo)有:模塊度(modularity)、強(qiáng)/弱社團(tuán)(community in a strong sense and in a weak sense)和聚類(lèi)系數(shù)(clustering coefficient)。
2.1 模塊度指標(biāo)
模塊度函數(shù)(Q函數(shù))是用來(lái)衡量復(fù)雜網(wǎng)絡(luò)社團(tuán)劃分質(zhì)量的標(biāo)準(zhǔn)[13],表示實(shí)際情況下社團(tuán)內(nèi)部連接強(qiáng)度與隨機(jī)連接情況下的社團(tuán)內(nèi)兩個(gè)節(jié)點(diǎn)連接強(qiáng)度的差異。對(duì)加權(quán)網(wǎng)絡(luò),模塊度函數(shù)定義為:
(1)
其中wij表示節(jié)點(diǎn)i與節(jié)點(diǎn)j連邊的權(quán)重,s為網(wǎng)絡(luò)中邊的權(quán)值之和,si表示與節(jié)點(diǎn)i所連接邊的權(quán)值總和,ci表示節(jié)點(diǎn)vi所在的社團(tuán),ci與cj相同時(shí),δ(ci,cj)=1,否則為0。Q值取值越接近1,社團(tuán)結(jié)構(gòu)越明顯,實(shí)際網(wǎng)絡(luò)中發(fā)現(xiàn)Q值大于0.3時(shí)具有較好的社團(tuán)劃分結(jié)果。
2.2 強(qiáng)/弱社團(tuán)指標(biāo)
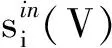
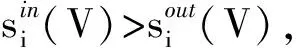
(2)
若子圖V滿足下述條件則其為弱社團(tuán):
(3)
如果針對(duì)某網(wǎng)絡(luò)的社團(tuán)劃分結(jié)果中滿足強(qiáng)/弱社團(tuán)定義的社團(tuán)小于等于1個(gè),則可判斷該網(wǎng)絡(luò)不具備社團(tuán)結(jié)構(gòu)或劃分結(jié)果不正確。因強(qiáng)社團(tuán)結(jié)構(gòu)同時(shí)也是弱社團(tuán)結(jié)構(gòu),因此可以通過(guò)弱社團(tuán)結(jié)構(gòu)總數(shù)占所有劃分的社團(tuán)結(jié)構(gòu)數(shù)量的比例來(lái)從一定程度上衡量社團(tuán)劃分效果。
2.3 聚集系數(shù)
聚集系數(shù)[15]反映了網(wǎng)絡(luò)中各節(jié)點(diǎn)的鄰居節(jié)點(diǎn)間的平均緊密程度,用來(lái)刻畫(huà)網(wǎng)絡(luò)節(jié)點(diǎn)的局部聚集程度,也可以用其衡量網(wǎng)絡(luò)整體或其子社團(tuán)的聚集程度。對(duì)于加權(quán)網(wǎng)絡(luò),聚集系數(shù)定義為:
(4)
其中,wij表示節(jié)點(diǎn)vi與vj間連邊的權(quán)值,si表示所有與節(jié)點(diǎn)vi相連的邊的權(quán)值之和。
可通過(guò)計(jì)算每個(gè)節(jié)點(diǎn)的聚類(lèi)系數(shù)進(jìn)一步求整個(gè)網(wǎng)絡(luò)的平均聚類(lèi)系數(shù)來(lái)體現(xiàn)網(wǎng)絡(luò)整體的聚集情況,同樣可以針對(duì)網(wǎng)絡(luò)中的每個(gè)社團(tuán)分別求其聚類(lèi)系數(shù)來(lái)衡量社團(tuán)聚集程度。一般網(wǎng)絡(luò)節(jié)點(diǎn)間連接越緊密,連接強(qiáng)度越高則聚類(lèi)系數(shù)越大。
3 實(shí)驗(yàn)及分析
為了分析加權(quán)復(fù)雜網(wǎng)絡(luò)上社團(tuán)劃分算法的特點(diǎn),實(shí)驗(yàn)時(shí)獲取了8個(gè)來(lái)自不同領(lǐng)域、規(guī)模不一的真實(shí)加權(quán)網(wǎng)絡(luò)數(shù)據(jù)集。由于真實(shí)的網(wǎng)絡(luò)中社團(tuán)數(shù)量未知,且存在層疊社團(tuán)的特征,因此實(shí)驗(yàn)中選擇基于模塊度優(yōu)化的GN算法、FN算法、CNM算法和BGLL算法進(jìn)行實(shí)驗(yàn),在運(yùn)行時(shí)間、模塊度、強(qiáng)弱社團(tuán)、聚集系數(shù)上進(jìn)行對(duì)比分析。
3.1 數(shù)據(jù)集分析
CELE(Celegansneural)為秀麗線蟲(chóng)神經(jīng)網(wǎng)絡(luò)的加權(quán)復(fù)雜網(wǎng)絡(luò)。
A-ph,C-mat,H-th為1995至1999年間www.arxiv.org上天體物理學(xué)、凝聚態(tài)、高能物理3個(gè)研究領(lǐng)域的科學(xué)家合作網(wǎng)絡(luò),合作的次數(shù)作為邊的權(quán)值。
Cros(cross-domain)為1990至2005年間5個(gè)領(lǐng)域(數(shù)據(jù)挖掘、醫(yī)學(xué)信息學(xué)、計(jì)算機(jī)理論、可視化、數(shù)據(jù)庫(kù))科學(xué)家發(fā)表論文的情況,合作的次數(shù)作為邊的權(quán)值。
G-au為aminer.org上的論文作者與作者之間的合作關(guān)系構(gòu)成,合作的次數(shù)作為邊的權(quán)值。
NDac為www.imdb.com上的127 823部電影參演信息,同時(shí)參演一部電影的次數(shù)作為邊權(quán)的權(quán)值。
NDw為nd.edu網(wǎng)站上網(wǎng)頁(yè)間的跳轉(zhuǎn)關(guān)系,可由同一個(gè)頁(yè)面跳轉(zhuǎn)的頁(yè)面數(shù)量作為邊權(quán)的權(quán)值。
上述數(shù)據(jù)及的統(tǒng)計(jì)特征如表2所示。

表2 數(shù)據(jù)集統(tǒng)計(jì)情況Table 2 Statistics of datasets
表2中N為節(jié)點(diǎn)數(shù),M為邊數(shù),
3.2 算法運(yùn)行時(shí)間分析
從表3可以看出,BGLL算法執(zhí)行時(shí)間最短,這與概算法中模塊度增益函數(shù)及迭代次數(shù)有關(guān),這也使得BGLL算法可以處理較大規(guī)模的圖片問(wèn)題。

表3 算法針對(duì)各數(shù)據(jù)集的耗時(shí)Table 3 Time consumption of algorithm for different datasets
3.3 模塊度指標(biāo)分析
從表4的結(jié)果可看出,每個(gè)數(shù)據(jù)集的社團(tuán)劃分結(jié)果基本都具有明顯的社團(tuán)結(jié)構(gòu),GN算法與其他3個(gè)算法所得出的結(jié)果在模塊度指標(biāo)上出入較大,F(xiàn)N算法與CNM算法所得到的社團(tuán)劃分結(jié)果的模塊度指標(biāo)數(shù)據(jù)相差無(wú)幾,這與CNM算法是基于FN算法進(jìn)行時(shí)間復(fù)雜度優(yōu)化而來(lái)的特點(diǎn)保持一致,BGLL算法在所有的數(shù)據(jù)集上表現(xiàn)最好。
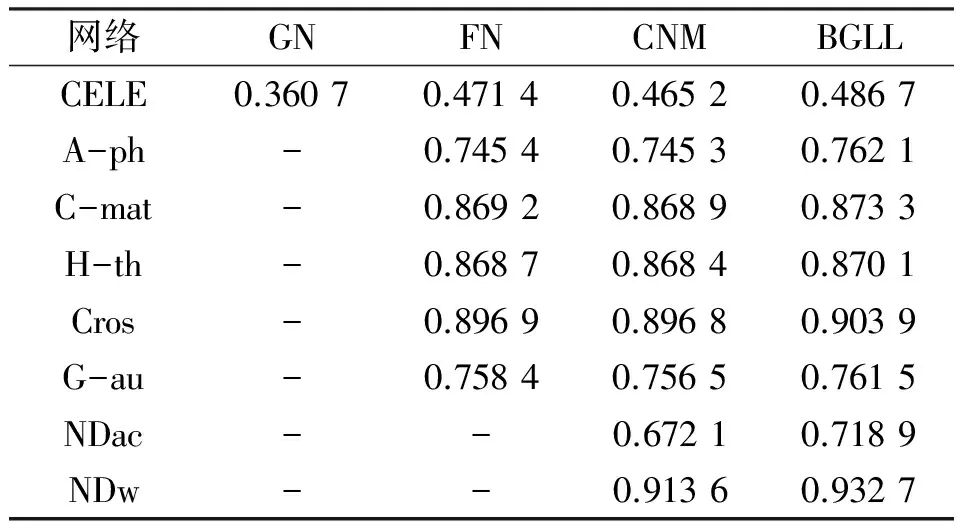
表4 社團(tuán)劃分結(jié)果模塊度統(tǒng)計(jì)數(shù)據(jù)Table 4 Statistics of different object modules
3.4 強(qiáng)/弱社團(tuán)指標(biāo)分析
表5給出了每個(gè)算法在各數(shù)據(jù)集中的強(qiáng)社團(tuán)、弱社團(tuán)和其他社團(tuán)的數(shù)量(強(qiáng)/弱/其他),其中BGLL算法中給的L1到L4分別表示4個(gè)層次的重疊社團(tuán)。從數(shù)據(jù)可以看出,所有算法的社團(tuán)劃分結(jié)果中弱社團(tuán)的數(shù)目都大于1,這說(shuō)明這些加權(quán)復(fù)雜網(wǎng)絡(luò)都具有社團(tuán)結(jié)構(gòu)。GN算法的結(jié)果中社團(tuán)數(shù)目相比其他算法多,但弱社團(tuán)數(shù)目相差無(wú)幾,這與GN算法的分裂過(guò)程特性有較大關(guān)系。在規(guī)模較大數(shù)據(jù)集的社團(tuán)劃分結(jié)果中有較多既不屬于強(qiáng)社團(tuán)也不屬于弱社團(tuán)的社團(tuán)結(jié)構(gòu),其中相當(dāng)部分社團(tuán)結(jié)構(gòu)都是離群點(diǎn),表明在真實(shí)復(fù)雜網(wǎng)絡(luò)中,離群點(diǎn)現(xiàn)象比較正常。此外,從BGLL算法的劃分結(jié)果可以看出該算法在第一層與第二層社團(tuán)層次結(jié)構(gòu)時(shí)社團(tuán)數(shù)目急劇減少,說(shuō)明在真實(shí)復(fù)雜網(wǎng)絡(luò)中層次越高,社團(tuán)聚類(lèi)的可能性越低。
3.5 聚類(lèi)系數(shù)指標(biāo)統(tǒng)計(jì)數(shù)據(jù)
表6給出了各算法社團(tuán)劃分結(jié)果中社團(tuán)的聚類(lèi)系數(shù)的均值,平均社團(tuán)聚類(lèi)系數(shù)越高,說(shuō)明所劃分出來(lái)的社團(tuán)結(jié)構(gòu)越緊密。從數(shù)據(jù)中可以看出FN與CNM的平均社團(tuán)聚類(lèi)系數(shù)相差無(wú)幾,BGLL所劃分的社團(tuán)結(jié)構(gòu)層次越高,聚類(lèi)系數(shù)越大,這與聚類(lèi)系數(shù)能夠反映網(wǎng)絡(luò)聚集程度的特性保持一致。而GN算法得出社團(tuán)劃分結(jié)果的聚集系數(shù)相對(duì)不理想,通過(guò)對(duì)GN算法所獲得的社團(tuán)劃分?jǐn)?shù)據(jù)分析,其原因是該社團(tuán)劃分結(jié)果中有相當(dāng)數(shù)量的社團(tuán)結(jié)構(gòu)僅由一個(gè)節(jié)點(diǎn)構(gòu)成。
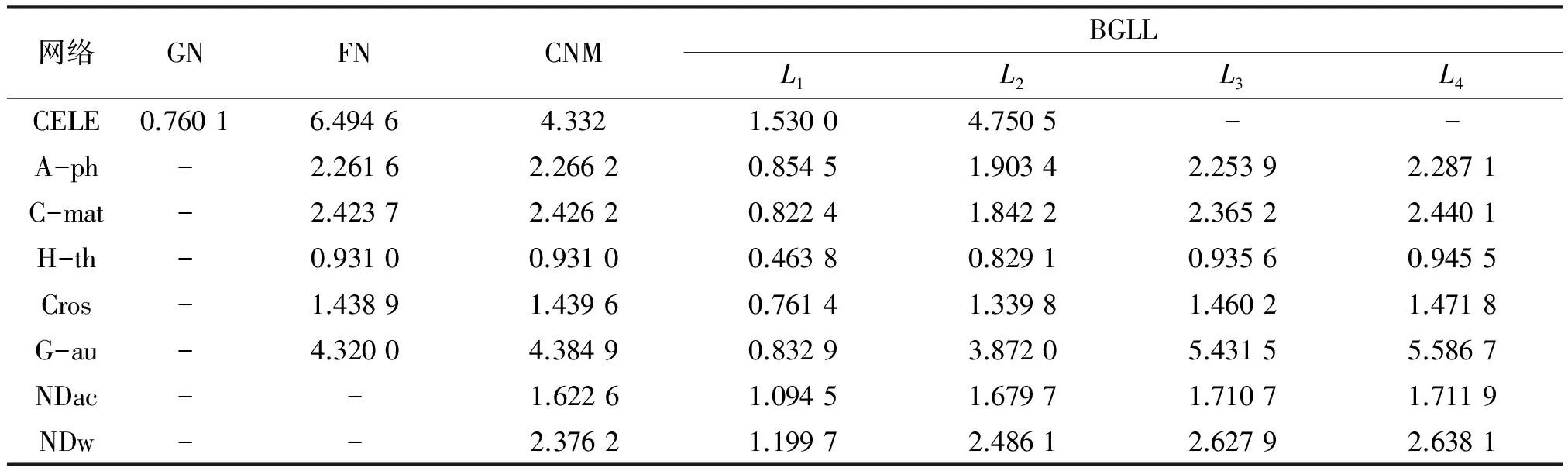
表6 社團(tuán)平均聚類(lèi)系Table 6 Community average clusters
4 結(jié)論
通過(guò)8個(gè)來(lái)自不同領(lǐng)域、規(guī)模不一的真實(shí)加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)劃分結(jié)果分析,可以看出文中的4種社團(tuán)發(fā)現(xiàn)算法都能夠在一定程度上挖掘出其中的社團(tuán)結(jié)構(gòu),但劃分出來(lái)的社團(tuán)數(shù)量與真實(shí)情況存在較大出入。因此,合理的定義社團(tuán)內(nèi)部與社團(tuán)外部的關(guān)系是社團(tuán)劃分結(jié)果優(yōu)劣的關(guān)鍵,真實(shí)復(fù)雜網(wǎng)絡(luò)中往往存在大量的噪音,影響社團(tuán)發(fā)現(xiàn)的過(guò)程,降低社團(tuán)發(fā)現(xiàn)的準(zhǔn)確度。如何根據(jù)網(wǎng)絡(luò)的特征,詮釋合理的社團(tuán)定義,去除網(wǎng)絡(luò)噪音將是此后的研究重點(diǎn)之一。
在模塊度,強(qiáng)/弱社團(tuán),聚類(lèi)系數(shù)3個(gè)評(píng)價(jià)指標(biāo)上,從針對(duì)CELE的劃分結(jié)果中可以發(fā)現(xiàn),F(xiàn)N與CNM的結(jié)果的模塊度Q值相差無(wú)幾,BGLL稍大于二者。但聚類(lèi)系數(shù)上FN與CNM平均聚類(lèi)系數(shù)相差較大,BGLL的平均聚類(lèi)系數(shù)位于兩者之間。而在其他數(shù)據(jù)集的社團(tuán)劃分結(jié)果上各統(tǒng)計(jì)指標(biāo)對(duì)劃分效果的衡量又能基本保持一致。由此可看出,各評(píng)估指標(biāo)在針對(duì)相同的社團(tuán)劃分結(jié)果上并不能始終保持一致的判斷,評(píng)價(jià)指標(biāo)是指導(dǎo)社團(tuán)發(fā)現(xiàn)過(guò)程、衡量社團(tuán)發(fā)現(xiàn)效果的重要參數(shù),如何優(yōu)化現(xiàn)有評(píng)價(jià)指標(biāo)或者找到新的評(píng)價(jià)指標(biāo)對(duì)加權(quán)復(fù)雜網(wǎng)絡(luò)的社團(tuán)劃分結(jié)果進(jìn)行更加有效的衡量也將是此后研究的重點(diǎn)之一。
本文討論的加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法都是基于模塊度優(yōu)化的算法,這類(lèi)算法的共同特點(diǎn)是都是以最大化模塊度Q值或者最大化局部模塊度Q值增益為目標(biāo),具有一定的貪婪特性,因此在算法決策時(shí)可能錯(cuò)過(guò)指向真實(shí)社團(tuán)結(jié)構(gòu)但并非局部最優(yōu)值的方向,從而導(dǎo)致算法的最終結(jié)果存在偏差。從實(shí)驗(yàn)結(jié)果中也可看出即便是針對(duì)社團(tuán)結(jié)構(gòu)清晰的加權(quán)復(fù)雜網(wǎng)絡(luò),比如跨領(lǐng)域科學(xué)家合作網(wǎng)Cros,社團(tuán)劃分結(jié)果依然存在大量的未被正確劃分的節(jié)點(diǎn),并且最終得到的社團(tuán)數(shù)量與實(shí)際偏差較大,這表明對(duì)于大規(guī)模復(fù)雜網(wǎng)絡(luò),基于優(yōu)化模塊度Q值的算法通常更傾向于找到復(fù)雜網(wǎng)絡(luò)中比較粗糙的社團(tuán)結(jié)構(gòu),而不是精準(zhǔn)的社團(tuán)結(jié)構(gòu)。
[1] WATTS D J, STROGATZ S H. Collective dynamics of small-world networks[J]. Nature, 1998, 393(6684): 440-442.
[2] BARABASI A, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.
[3] 李曉佳, 張鵬, 狄增如,等. 復(fù)雜網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)[J]. 復(fù)雜系統(tǒng)與復(fù)雜性科學(xué), 2008(3): 19-42.
[4] ZOLLMAN K J. The communication structure of epistemic communities[J]. Philosophy of Science, 2015, 74(5): 574-587.
[5] HUANG L, LI R, CHEN H, et al. Detecting network communities using regularized spectral clustering algorithm[J]. Artificial Intelligence Review, 2014, 41(4): 579-594.
[6] VIEIRA V D, XAVIER C R, EBECKEN N F, et al. Performance evaluation of modularity based community detection algorithms in large scale networks[J]. Mathematical Problems in Engineering, 2014.
[7] MEJ N. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004, 69(6): 066133.
[8] CLAUSET A, NEWMAN M E J, MOORE C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70(6): 66111.
[9] BLONDEL V, GUILLAUME J, LAMBIOTTE R, et al. Fast unfolding of community hierarchies in large networks[J]. ArXiv, 2008.
[10] 楊博, 劉大有, 金弟,等. 復(fù)雜網(wǎng)絡(luò)聚類(lèi)方法[J]. 軟件學(xué)報(bào), 2009, 20(1): 54-66.
[11] 田柳, 狄增如, 姚虹. 權(quán)重分布對(duì)加權(quán)網(wǎng)絡(luò)效率的影響[J]. 物理學(xué)報(bào), 2011, 60(2): 803-808.
[12] 呂天陽(yáng), 謝文艷, 鄭緯民,等. 加權(quán)復(fù)雜網(wǎng)絡(luò)社團(tuán)的評(píng)價(jià)指標(biāo)及其發(fā)現(xiàn)算法分析[J]. 物理學(xué)報(bào), 2012, 61(21): 145-154.
[13] NEWMAN M E J. Communities, modules and large-scale structure in networks[J]. Nature Physics, 2012, 8(1): 25-31.
[14] CAFIER S, CAPOROSSI G, HANSEN P, et al. Finding communities in networks in the strong and almost-strong sense[J]. Physical Review E, 2012.85(4):52-58.
[15] SONG Y, LIU J, YU Z, et al. Multifractal analysis of weighted networks by a modified sandbox algorithm[J]. Scientific Reports, 2015,(5): 17628.
The Community Discovery Algorithm Analysis on Weight Complex Network based on Modularity Optimization
YANG Chunming, WANG Yujing
(SchoolofComputerScienceandTechnology,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan,China)
Community structure is an important topology of complex networks. Aiming at the community discovery problem of weight complex networks, this paper analyzes modularity optimization algorithm of GN, FN, CNM, BGLL form modularity, strong/weak community, clustering coefficient evaluation in 8 different domains and different sizes of real-world datasets. The result shows that the existing criterions encounter difficulties in evaluating the weighted community with complex structure, and these algorithms are more likely to find crude community structure in complex networks, rather than precise community structure. The generalization of the algorithm still needs to be strengthened.
Weight complex network; Community discovery; modularity; clustering coefficient
2013-12-23
楊春明(1980—),男,副教授,碩士,CCF會(huì)員(18297M),研究方向?yàn)樗惴ㄔO(shè)計(jì),知識(shí)工程,E-Mail:yangchunming@swust.edu.cn
TP301.6
A
1671-8755(2016)04-0084-06

