翻轉(zhuǎn)課堂在高等數(shù)學教學中的幾點體會
——以測控151班級為例
張育藺
(南京信息職業(yè)技術(shù)學院素質(zhì)教育部,江蘇 南京210023)
翻轉(zhuǎn)課堂在高等數(shù)學教學中的幾點體會
——以測控151班級為例
張育藺
(南京信息職業(yè)技術(shù)學院素質(zhì)教育部,江蘇 南京210023)
翻轉(zhuǎn)課堂教學法是信息化時代的一種新的教學方法,是對傳統(tǒng)的課堂教學教學方法的完善與補充。本文是在上學期測控151班級實踐的基礎(chǔ)上,得到的一些教學體會和心得。旨在通過這種教學方法,提高學生的學習興趣和學習效率。
翻轉(zhuǎn)課堂;微課;高等數(shù)學
所圍翻轉(zhuǎn)課堂,就是教師創(chuàng)建視頻,學生在課外觀看視頻中教師的講解,回到課堂上師生面對面交流和完成作業(yè)的一種教學形態(tài)。最早是在美國科羅拉多州落基山的一個山區(qū)學校——林地公園高中,教師們常常被一個問題所困擾:有些學生由于各種原因,時常錯過正常的學校活動,且學生將過多時間花費在往返學校的巴士上。這樣導致很多學生由于缺課而跟不上學習進度。直到有一天,學校的兩個老師開始使用屏幕捕捉軟件錄制PPT演示文稿的播放和講解、他們把結(jié)合實時講解和PPT演示的視頻上傳到網(wǎng)絡(luò),以此幫助課堂缺課的學生補課。后來,兩位教師逐漸以學生在家看視頻聽講解為基礎(chǔ),節(jié)省出課堂時間來為在完成作業(yè)或做實驗中有困難的學生提供幫助。這種教學方式現(xiàn)在受到越來越多人的關(guān)注,逐漸成為一種新興的教學模式,這種教學模式和傳統(tǒng)的課堂教學方法相結(jié)合,將學生由被動轉(zhuǎn)為主動,極大地提高了學生的學習興趣,提高學習效率。
本學期我在課題組的推動下在測控151班級進行了翻轉(zhuǎn)課堂的實踐與探索。在高等數(shù)學教學實踐中,我也不是一刀切地全部運用翻轉(zhuǎn)課堂教學,而是選取了幾種特殊的課進行嘗試,以此推進課程改革。一學期下來,我發(fā)現(xiàn)收效相當?shù)拿黠@,學生越來越喜歡上數(shù)學課了。下面介紹幾節(jié)我認為比較成功的案例,分別是概念教學課,典型例題、習題的教學課,復習指導課。
1 概念教學課
數(shù)學概念是數(shù)學學習的魂,是學生學習數(shù)學、接受新知識的基礎(chǔ)。準確而又徹底地理解和掌握數(shù)學課堂學習中的概念是學生學好數(shù)學及后續(xù)專業(yè)課程的必備條件。但由于概念課比較抽象,學生普遍感覺比較枯燥,再加上班級學生的層次良莠不齊,很多概念不能理解,掌握的效果也差強人意,這極大地影響了后面的學習。如何能讓學生在徹底理解的基礎(chǔ)上使學生把概念記牢,重要的是要把概念翻譯得通俗易懂,能夠舉一反三、融會貫通,從而理解概念的內(nèi)涵和外延。這一點可以利用翻轉(zhuǎn)課堂來實現(xiàn)。要講概念課之前,我們可以先把概念用通俗易懂的語言錄制好視頻,讓學生可以隨時隨地地回顧概念,對學生掌握數(shù)學概念很有幫助。例如函數(shù)的極限定義,非常的抽象,學生很難理解這種數(shù)學語言定義的概念,而函數(shù)極限概念又是《高等數(shù)學》這門課程中一個重要的知識點,在《高等數(shù)學》中,幾乎所有基本概念(如連續(xù)、微分、積分)都是建立在函數(shù)極限概念的基礎(chǔ)之上,極限的思想方法是研究變量的最基本方法。故極限概念學習的好壞直接影響后面知識點的學習,這時我們就可以采用翻轉(zhuǎn)課堂的模式來學習本節(jié)內(nèi)容。首先在上課前我們先錄一段函數(shù)極限概念講解的微課,微課將分別從函數(shù)極限概念的推導以及使用兩個方面來介紹函數(shù)極限。講到函數(shù)的極限定義時,微課中首先認識函數(shù)極限概念的描述性定義,然后通過類比、例題分析引入了函數(shù)極限概念的精確定義,即用定量的數(shù)學語言來描述無限接近,接下來通過幾何直觀進一步闡述函數(shù)極限概念,利用例題及動畫加深對概念的理解,最后總結(jié)了對定義的幾點說明及使用定義證明函數(shù)極限的步驟,加深對函數(shù)極限概念的理解。在教學平臺上可以寫幾個簡單的例子,先讓學生熟悉一下解題思路和步驟。到上課的時間先了解學生的學習情況,組織學生進行討論,根據(jù)學生掌握的情況因人制宜地進行講解。最后再復習總結(jié)。這樣下來學生對本概念的理解就比較深刻,掌握的效果也會比較好。
2 典型例題、習題教學
創(chuàng)設(shè)和選取典型例題是數(shù)學課堂教學環(huán)節(jié)中一個必不可少的重要環(huán)節(jié)。創(chuàng)設(shè)典型的例題是數(shù)學學科的教學特點,它不但可以收到事半功倍的效果.還可以逐步培養(yǎng)學生的知識遷移能力。通過典型例題的解題思路學生還能學到一些解題技巧,加深對知識點的理解和掌握。這時我們就可以通過翻轉(zhuǎn)課堂的模式實現(xiàn)這一點,首先我們先根據(jù)這一節(jié)的習題特點選擇幾個典型的例題,錄成微課,學生在課下完成之后,課上可以根據(jù)他們的做題情況有重點地講解,省下的時間就可以分組比賽等等,通過其他形式的做題目調(diào)動學生學習的積極性,從而達到較好的學習效果。例如在《高等數(shù)學》下冊部分,二重積分,三重積分,曲線積分,曲面積分放在一起學習,學生很容易混淆,感覺學習起來很困難,這就可以充分利用習題課的時間,幫助學生把知識點串一串。為此我做了一個視頻,先把所有知識點(一)重積分的性質(zhì);(二)二重積分的計算方法:(1)直角坐標(2)極坐標;(三)三重積分的計算方法;(四)對弧長的曲線積分的計算方法;(五)對坐標的曲線積分的計算方法 (兩類曲線積分之間的關(guān)系);(六)格林公式、斯托克斯公式;(七)對面積的曲面積分的計算方法;(八)對坐標的曲面積分的計算方法(兩類曲面積分之間的關(guān)系);(九)高斯公式;(十)重積分的應(yīng)用(面積、體積、質(zhì)心、轉(zhuǎn)動慣量、引力);(十一)梯度、散度、旋度。羅列出來,各個知識點之間的聯(lián)系,如何應(yīng)用都清楚明了地表達出來,讓學生先對內(nèi)容有一個回顧復習。比如說,這一章的格林公式和高斯公式學生不是很理解,不能熟練應(yīng)用。這時我就單獨做了一個小視頻,把格林公式,高斯公式和他們比較熟悉的牛頓——萊布尼茲公式建立聯(lián)系。
眾所周知,設(shè)f(x)在區(qū)間[a,b]上連續(xù),F(xiàn)(x)是f(x)在[a,b]上的一個原函數(shù),則

這個公式就是大家非常熟悉的牛頓——萊布尼茲公式。它告訴我們:要計算f(x)在區(qū)間[a,b]上積分值,不需要考慮這個區(qū)間的內(nèi)部,只需要考慮區(qū)間的兩個端點a和b,它等于原函數(shù)在兩個端點的函數(shù)值之差,這就大大降低了難度。
格林公式和高斯公式呢?是高維時的情況。格林公式:設(shè)閉區(qū)域D由分段光滑的曲線L圍成,函數(shù)P(x,y)與Q(x,y)在D上具有一階連續(xù)偏導數(shù),則有
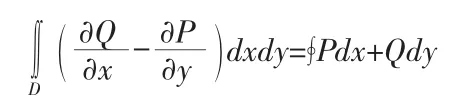
其中L是D的取正向的邊界曲線。很容易可以看出:類似于牛頓——萊布尼茲公式,格林公式是把區(qū)域D上的二重積分轉(zhuǎn)化到其邊界曲線L上去進行,與區(qū)域內(nèi)部沒有關(guān)系。同時它也把二重積分降為定積分去計算,這就大大降低了計算的難度。
同理,對于高斯公式:設(shè)空間閉區(qū)域Ω是由光滑或分片光滑的閉曲面Σ所圍成,函數(shù)P(x,y,z),Q(x,y,z),R(x,y,z)在Ω上具有一階連續(xù)偏導數(shù),則

這里Σ是Ω的整個邊界曲面的外側(cè)。它把空間區(qū)域Ω上的三重積分轉(zhuǎn)化到邊界曲面Σ上去進行,與區(qū)域內(nèi)部無關(guān),同時它也把三重積分降為二重積分去計算,這也降低了計算的難度和工作量。綜上所述,這三個定理本質(zhì)上是一樣的,都是把區(qū)域或區(qū)間上的定積分轉(zhuǎn)化為其邊界或端點去考慮。這樣一講,學生就能對格林公式和高斯公式加深了理解,掌握起來就相對容易多了。
接下來羅列出一些基本的典型例題,讓學生課下先討論解決,到上課的時間就讓學生自己講解自己做的題目和遇到的困難,在師生共同參與下完成對重積分的復習學習。最后可以再列舉一些有梯度的題目,讓學生課后根據(jù)自己的情況認真完成。這樣下來,學生普遍感覺有信心多了,對知識點的掌握也更牢固。并且這些視頻到最后復習考試的時間,也非常的有用。
3 復習指導
在總復習時,我們也會遇到很多的問題,但主要是時間少、內(nèi)容多。學生基礎(chǔ)參差不齊,復習迎考的態(tài)度也是千差萬別。如何讓每位學生在復習階段都有所提升,都能考取自已理想的成績是我們每個老師都要面臨的問題。如何能在最短的時間使每個學生都能提高復習效率,我在上學期的期末復習時嘗試了翻轉(zhuǎn)課堂教學的嘗試。《高等數(shù)學》下冊期末考試知識點多,并且比較難,有不少學生在學習的時間就沒掌握太好,復習的時間又非常短。針對這種特點,我首先做了一個視頻,把這一學期的框架圖及主要知識點告訴學生,讓他們在復習的時間有的放矢,不至于沒有目標。接下來針對每個知識點及考試的要求模擬幾套試卷,讓學生在課下單獨完成,自己發(fā)現(xiàn)問題。到上課的時間互評,自評相結(jié)合,找出自己的問題,解決問題,在老師和同學們的幫助下,每個同學都達到了自己的預期,效果很好。
以上是我在上學期測控151班級《高等數(shù)學》翻轉(zhuǎn)課堂教學探索中比較成功的案例,雖說達到了一定的效果,但也不是特別滿意,還有很大的進步空間和要改善的地方。希望翻轉(zhuǎn)課堂能以信息技術(shù)作為外在條件,完善傳統(tǒng)教學的一些弊端,喚起學生學習的熱情,讓學生真正愛上學習。
[1]夏大峰,等.高等數(shù)學[M].高等教育出版社,2013.
[2]胡鐵生.微課:區(qū)域教育信息資源發(fā)展的新趨勢[J].電化教育研究,2011.
[3]張金磊.翻轉(zhuǎn)課堂教學模式研究[J].遠程教育雜志,2012.
[4]卜彩麗.翻轉(zhuǎn)課堂教學模式在我國高等院校應(yīng)用的可行性分析[J].軟件導刊, 2013.
[責任編輯:朱麗娜]
江蘇省高等教育教改研究課題(批準號:2015JSJG381)。

