有效數學作業設計初探

◆方慶榮

(福建省龍海市石碼中心小學)

有效數學作業設計初探

◆方慶榮

(福建省龍海市石碼中心小學)

數學作業的有效性體現在兩個方面：第一，作業的內容選擇，形式設計，數量控制必須有助于學生當下的發展。第二，學生喜歡并樂于完成，做作業過程中伴有愉悅的感受,如驚喜、敢挑戰、成就感等。因此，設計作業必須做到重點突出，層次分明，有針對性和實踐性。

有效作業 重點突出 層次分明 針對性 實踐性

新課標要求作業的內容要緊密聯系學生的學習、生活實際，設計形式新穎，能激發學生的學習興趣，發展創新思維，給學生更多的自主選擇，讓作業成為學生成長的內在需要。現在我就談談在數學作業設計上的淺見。

一、練習設計要突出重點

每個新知識的形成大都帶有舊知識的成分，因此，教師必須科學解讀文本，對教材進行再創造，精心設計習題，使學生更容易理解新知識的內在含義，并能靈活加以應用。

1.抽絲剝繭，由表及里

教材中，有些例題必須要做分解，呈現知識的形成過程，否則，學生雖然會按書中的解法“依樣畫葫蘆”解答一些題目，但并不真正明白其中的算理，即所謂“知其然而不知其所以然”，遇到更復雜的應用時，就暈頭轉向。

2.辨析優化，去偽存真

有些新知識在學習之后，如果題目的形式或條件有所變化，學生的思維又會受到舊解題思路的干擾，出現思路“打架”現象。這時，教師可圍繞知識重點設計對比訓練，達到明辨是非、加深記憶的效果。

二、練習設計要層次分明

學生學習新知體現由簡單到復雜的上樓梯形態。所以，設計的練習題要有梯度。

1.夯實基礎，循序漸進

在學習“比的應用”后，設計以下課堂練習：

①800平方米的菜地按1∶3種大蒜和西紅柿。兩種菜的面積各有多少平方米？

②甲、乙、丙三人的歲數比是4∶5∶7，已知乙是15歲，甲、丙各幾歲？

③李明、王芳兩人的存錢比是5∶3，李明比王芳多60元，兩人共存多少元？

這些基本題目是讓學生適應比的一般應用，重點讓學生感悟具體量與比份的對應性，題目的呈現形式及問題難度由淺漸深，激發學生的作業熱情。

2.綜合拓展，鉤深致遠

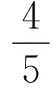
這些題目把比的知識與幾何圖形、分數、極值問題結合起來，延伸書本知識，把比的應用提高到更高的層次，使學生在作答中意志得到磨練，感受數學知識應用的精妙，促使觸類旁通，培養勇攀數學高峰的品質。

三、練習設計要有針對性

在教學中經常會遇到這種情況，學習一個新知識后，學生對模仿性的練習做得很好，但是，在做綜合練習題時，有的就不知從何入手，思路出現“卡殼”，教師必須抓住“癥結”所在，設計的作業要有針對性。

1.巧解結點，融會貫通

在學習了圓的知識后，設計下面練習：

①據“甲、乙圓的半徑比2:3”，說出甲、乙圓的直徑比、周長比和面積比；

②某圓直徑擴大2倍，半徑擴大( )倍，周長擴大( )倍，面積擴大( )倍。

當練習講評后，學生明白兩個圓的半徑比等于它們的直徑比，也等于它們的周長比，而它們的面積比是它們半徑比的平方比。這樣就從多方面、多角度地理解圓的相關量的變化規律，當遇到以下題目就思路順暢，并且能一題多解。

2.題組訓練，破解定勢

學生頭腦中有了思維定勢傾向，就會造成思維僵化和呆板，阻礙數學思維的發展。我常采用題組進行訓練，破解思維定勢。

如教學“往返的行程問題”時，出如下題組：

①甲、乙兩地相距540千米，李叔叔駕車從甲地到乙地，去時用6小時，返回用4小時,求李叔叔駕車往、返兩地的平均時速。

②鄭老師爬山，從山腳到山頂用35分鐘；沿原山路下山，25分鐘走到山腳。已知上山每分鐘爬45米，問：鄭老師上、下山平均每分鐘行多少米？

③王宏家到學校相距1200米，上學每分鐘走80米，放學每分鐘走60米，求王宏上、放學平均每分鐘走幾米？

四、練習設計要有實踐性

新課程標準指出,學生學習應當是一個生動活潑的、主動的和富有個性的過程。學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程。

1.自主參與，動力十足

在教學“扇形統計圖”時，我只是提出一個作業框架：圍繞一個主題，可個人或四人組合作，調查搜集數據，再制成扇形統計圖。結合統計圖，總結調查結果，提出整改意見。學生自主選擇設計作業，作業內容豐富多彩:有的統計全班學生的身高，有的統計自己歷次考試的成績，有的統計全班學生上、放學的交通方式，有的統計全班學生的視力情況……學生學習熱情高漲，促使他們積極主動去應用數學知識，從中體會作業的樂趣。

2.跨科整合，開闊空間

新課程標準在總目標指出，數學本身與其他學科有著密切的聯系，作業設計不能只注重本學科的內容，應與其他學科進行整合，融智育、體育、美育、思品教育于一體，增強趣味性。

教完“比例尺的應用”后，把課后一道練習“畫出你家的平面圖”改裝成一道親子活動作業。學生完成這樣的作業，綜合應用數學、美術、思品等學科知識，從小課堂走向大社會，開闊了學習、應用數學的空間。在親子合作中，雙方都感受到合作的快樂。

總之，要使作業有效，設計時應該做到重點突出，層次分明，有針對性和實踐性。也只有做到這些，學生才會心甘情愿地接受并樂在其中，使智力、情感、價值觀等方面得到共同發展。

[1]全日制義務教育《數學課程標準》(實驗稿).

[2]小學數學教師.2014.

[3]布魯納著.教育的過程.