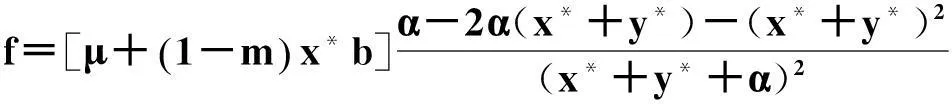具有Allee效應的合作進化

張瑞玲，王萬雄，2，*，秦麗娟，2

1 甘肅農業大學, 資源與環境學院，蘭州　730070

2 甘肅農業大學, 理學院，蘭州　730070

具有Allee效應的合作進化

張瑞玲1，王萬雄1，2，*，秦麗娟1，2

1 甘肅農業大學, 資源與環境學院，蘭州730070

2 甘肅農業大學, 理學院，蘭州730070

摘要:Allee效應對物種的續存是潛在的干擾因素，在很大程度上將增加種群局部甚至全局滅絕的可能性。對許多物種，尤其是瀕臨物種更容易受其影響。將Allee效應引入囚徒困境博弈模型，通過理論分析與數值模擬相結合的方法分析討論了Allee效應對合作進化的影響。研究結果表明：在惡劣的環境條件下，Allee效應極易使物種滅絕，不利于合作進化；在相對優越的環境條件下(死亡率較低)，Allee效應促進合作進化，且Allee效應強度越強，更有利于合作進化，不過種群的空間斑塊占有率也會隨著Allee效應強度的增強而降低，使物種最終滅絕。

關鍵詞：Allee效應；囚徒困境博弈；合作進化；死亡率

達爾文生物進化論的核心是自然選擇學說——物競天擇、弱肉強食。物種在生存競爭的過程中,經過自然選擇的作用,逐漸產生更能適存的物種,實現生物的進化。大自然中存在著競爭與矛盾沖突, 合作行為是生物體有利于其它個體的各種行為策略，是社會性生物的一個重要特征。合作進化機理是長期困擾進化生物學的一個難題，問題的關鍵是合作如何通過自然選擇從背叛種群中進化出來，及合作個體怎么才能避免背叛個體的剝削，從而抵制它們的入侵！囚徒困境的博弈不僅是博弈論中最具代表性的例子，而且作為研究合作進化的一個普遍范式[1]。

此外，Allee[2]指出，群聚有利于種群的增長和存活，每個生物都有自己的最適密度，其過分稀疏和擁擠都會對生殖發生負作用，阻止生長。Allee效應的產生源于很多方面的不利因素[3]，例如，配偶，生殖能力，過度掠奪，環境條件，同系繁殖等等。對于一個具有Allee效應的種群來說，當種群密度低于某一閾值時，物種將會滅絕，也就是說該種群具有一個足以維持生存的最低密度。尤其那些瀕危的哺乳類種群，其種群稀疏，更容易受到Allee效應的影響。許多理論研究表明Allee效應在種群動力學研究中存在強大的潛在影響，這引起了生態學家的廣泛關注[4- 5]。關于Allee效應對種群生態學系統穩定性的影響的研究也越來越受到人們的重視[6- 9]。因此，考慮到Allee效應和合作行為的進化分別是種群生態學和進化生物學的重要理論問題。Feng Zhang[10]等人做了囚徒困境博弈中的生態進化反饋和入侵的研究，結果表明：合作行為在密度依賴選擇的條件下更容易進化，該工作沒有涉及種群受Allee效應影響下的合作行為的進化，為了使模型更加切合實際。本文提出了受Allee效應影響的囚徒困境博弈模型，并利用動力模型分析及數值模擬方法對新建模型的基本性質進行初步研究，說明Allee效應對合作進化的影響，豐富了合作行為的演化動力學理論。

1模型建立

1.1生態囚徒困境博弈模型

生物界中，不論在同一種生物內部還是不同的物種之間，從低等的微生物到高等的多細胞生物都有合作行為的存在。盡管合作可以給群體帶來利益，但合作者遇到背叛者不可避免地付出代價。因此，合作行為進化的關鍵問題存在兩方面：一方面，如何從背叛者組成的種群中通過自然選擇進化產生合作行為？另一方面，合作種群如何有效地抵制背叛個體入侵？

囚徒困境博弈是合作行為進化的隱喻，假設種群由合作(C)和背叛(D)的個體組成，合作個體自身付出一定的代價c，對和它相互作用的對方產生利益b(b>c>0)，然而，背叛個體即不付出代價也不會產生利益。這兩種行為的囚徒困境博弈的贏得矩陣為：

定義合作個體與背叛個體分類相遇的概率[11]：

(1)一個個體遇到采取同樣策略個體的概率是m；

(2)一個個體隨機遇到其他個體(包括采取同樣策略的個體)的概率是1-m。

Feng Zhang, Cang Hui[10]研究了合作個體在囚徒困境博弈中的生態進化反饋及入侵，動力系統模型由如下的微分方程表達：

(1)

對系統(1)通過理論分析與數值模擬，結果表明：個體間的分類是至關重要的，同時高死亡率和低的種群占有率更能促進合作進化。

1.2種群具有Allee效應的合作進化模型

(2)

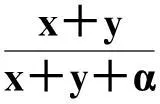
易驗證，在分類相遇m>0且密度依賴選擇(x+y<1)的情形下，有利于合作行為的進化。進一步通過計算可得系統(2)的平衡點如下：

(1)E(0,0)，合作行為與背叛行為都滅絕；

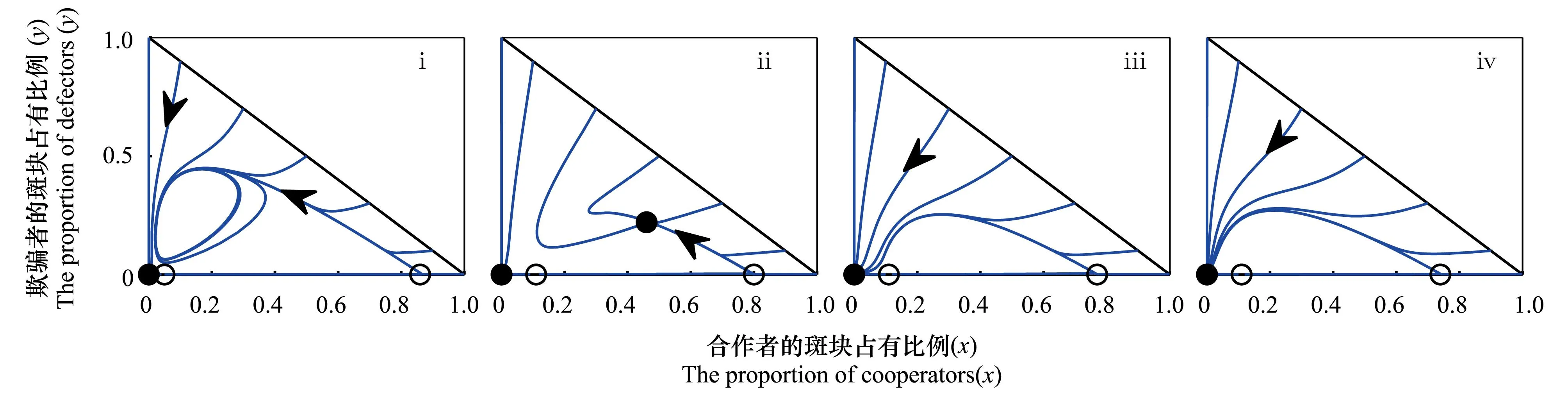
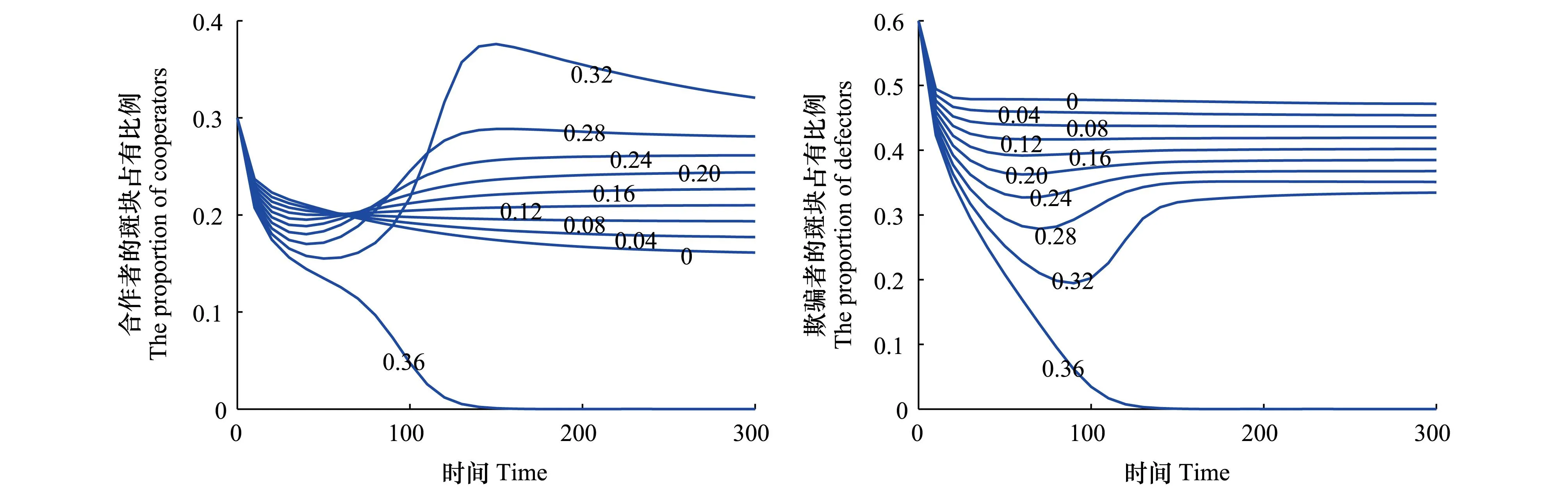
(2)最多存在四個邊界平衡點：(ⅰ)當δ<μ且(δ-μ)2>4μδα時，存在四個邊界平衡點(其中，兩個平衡點是背叛行為獨存，兩個平衡點是合作行為獨存)，(ⅱ)當μ+m(b-c)

(3)最多存在一個內部平衡點(x*,y*)，其中：

且滿足條件:

代表合作行為與背叛行為共存。如果mb>c，系統不存在內部平衡點。

平衡點(x*,y*)的雅克比行列式為:

λ2-trλ+det=0

其中,

由于det>0，則當tr2-4det>0且tr>0，平衡點(x*,y*)為不穩定的結點；當tr2-4det>0且tr<0，平衡點(x*,y*)為穩定的結點；當tr2-4det<0且tr>0，平衡點(x*,y*)為不穩定的焦點；當tr2-4det<0且tr<0，平衡點(x*,y*)為穩定的焦點。由此易知，系統(2)最多存在一個內部平衡點，隨著參數的變化，內部平衡點會從一個結點演化成一個焦點，即若tr2-4det=0，系統(2)出現分叉現象。與此同時，內部平衡點由穩定狀態向不穩定狀態演變，即若tr=0，系統(2)存在極限環。與系統(1)相比，Allee效應對合作進化是一個潛在的干擾因素。由于參數的繁雜，很難推斷出Allee效應具體如何影響合作進化及系統(1)的穩定性。因此，利用Matlab軟件對系統(2)進行數值模擬。

2數值模擬與結果分析

為了定性討論Allee效應對合作進化的影響，取文獻[10]中的參數μ=0.1,m=0.1,b=1,從系統(2)的演化結果可知，在Allee效應α=0.05的影響下，系統(1)中由于合作行為的高死亡率與高代價(c=0.3,δ=0.09)產生的阻尼振蕩(即焦點)變成周期性振蕩(即極限環,圖1-ⅰ)；更高的死亡率(c=0.25,δ=0.15)產生的阻尼振蕩將會消失，種群滅絕(圖1-ⅲ)；而合作行為的更高代價(c=0.39,δ=0.137)產生的周期性震蕩也會消失，種群滅絕；在較低的死亡率和代價(c=0.25,δ=0.15)條件下，Allee效應對系統的影響不大，系統(2)出現一個臨界值，當初值大于這個臨界值時，系統仍然存在一個穩定的內部平衡點(圖1-ⅱ)。由此可知，在惡劣的環境條件下，若種群由于尋找配偶的困難，社會功能異常，近交衰退等原因受Allee效應的影響時，更容易導致物種滅絕，影響生物的多樣性。

由圖(2-ⅰ)可見，取參數μ=0.1,m=0.1,b=1,c=0.15,δ=0.15，不受Allee效應影響時，系統存在一個穩定的結點；然而，在Allee效應常數α=0.05時，若合作種群與背叛種群的初始占有率大于某個臨界值(圖1-ⅱ)，Allee效應更容易使系統達到穩定狀態，促進合作進化(圖2-ⅱ)；繼續增強Allee效應(α>0.077)，就會導致種群滅絕，不利于合作進化(圖2-ⅲ)。說明在環境較為優越的條件下，適當的Allee效應促進合作進化，而繼續增強Allee效應將會導致物種滅絕。

圖1　受Allee效應α=0.05影響下系統(2)的演化相圖Fig.1　The evolutive phase diagram of system (2) with Allee effect α=0.05參數取值：μ=0.1,m=0.1,b=1, (ⅰ) c=0.3,δ=0.09;(ⅱ)c=0.15,δ=0.15; (ⅲ)c=0.25,δ=0.15; (iv)c=0.39,δ=0.137

空間網格上的博弈行為是近年進化博弈研究的新焦點[13]，基本思想是把種群安置在規則的空間網格上，一部分斑塊只有一個采取特定策略的個體占有，所有個體只和它局部相鄰斑塊上的個體相互作用，根據它們的總贏得和鄰體中個體的總贏得決定下一次所采取的策略。取參數μ=0.1,m=0.1,b=1, c=0.15,δ=0.09，對未受Allee效應及受不同Allee效應強度影響的空間囚徒困境博弈，在200×200的空間網格上，只考慮相鄰于每個斑塊邊的4個斑塊(馮諾伊曼鄰體)，進行時間t=200的空間數值模擬(圖3)。由圖3可見，當系統未受Allee效應影響時，除了少數的空斑塊，斑塊全部被合作策略及背叛策略的個體占有。當種群受Allee效應(α=0.05)影響時，空間中空斑塊的數量明顯增多，合作個體的占有比率有所增加。然而，繼續增加Allee效應(α=0.15)，空間的絕大部分斑塊未被占有，成為空斑塊，只有極少數的被種群占有；再繼續增加Allee效應，將導致物種滅絕。

下面將詳盡地討論Allee效應在未使物種滅絕的情況下，如何促進合作行為的進化，如圖4所見，當時間t<80時，Allee效應抑制合作進化；當時間t>80時，Allee效應促進合作進化，且隨著Allee效應強度的增強，合作個體的斑塊占有率逐漸增多。然而，對于背叛個體，Allee效應強度越強，其斑塊則占有率越低。若Allee效應強度大于0.335時，物種滅絕。

圖2　受Allee效應影響的系統(2)的演化曲線Fig.2　The evolvement curves of system (2) with Allee effect參數取值：μ=0.1,m=0.1,b=1,c=0.15,δ=0.15, Allee效應: (ⅰ)α=0;(ⅱ)α=0.05;(ⅲ)α=0.15

圖3　在200×200網格上，受Allee效應影響的空間囚徒困境在時間t=200的空間格局Fig.3　At time t=200, spatial patterns of spatial Prisoner′S Dilemma with Allee effect on a 4016401 lattice

圖4　合作個體、背叛個體對Allee效應變化(α=0,0.04,0.08,…,0.36)的相應響應Fig.4　The response of cooperators and defector under the change of Allee effec (α=0,0.04,0.08,…,0.36)參數取值：μ=0.1,m=0.1,b=1,c=0.15,δ=0.09

以上的數值模擬和預測說明，Allee效應對合作進化的影響顯著，對種群的續存是不可忽視的干擾因素[14]。與沒有受Allee效應的系統(1)相比，Allee效應破壞原來的平衡，形成新的平衡。合作個體在高代價、高死亡的條件下，Allee效應使以阻尼振蕩的相互作用共存的兩種行為策略變成周期性振蕩的共存模式；在更高死亡率和代價的環境中，Allee效應使博弈共存的物種滅絕。但是，在優越的環境條件下(即死亡率較低)，Allee效應反而促進合作進化，且Allee效應的強度越強越有利于合作行為的進化，不過種群的總體斑塊占有率會越低。與此同時，Allee效應強度過強，就會導致物種滅絕，行為策略不復存在。也就是說強Allee效應不僅減少物種的多樣性，而且影響生物進化。

3結論

Allee效應是種群動力學中的一個重要的調節機制：低的種群密度使雌雄個體相遇機會減少，尋覓配偶的困難大大增加[15](例如在防治橘小實蠅蟲害的過程中，就采用了釋放不育雄蟲制造Allee效應的措施)，對于植物來說同樣也會由于低密度使授粉成功的機會大大減少。非洲野狗是一種典型的群居動物，它們具有群體合作哺育后代、合作覓食的習性，過小的種群規模致使某些合作技能喪失，不能維持種群個體的生存。一定的種群規模也有利于抵御敵害，增加群體的反捕食的能力。很多自然界的物種曾被報導過具有Allee效應，比如植物[16]，海洋無脊椎動物[17]，昆蟲[18]，哺乳動物[19]等。正是因為Allee效應在現實生物種群中是普遍存在的，加之合作進化并不是一個進化穩定策略，在一次囚徒困境博弈中，不論對方采取什么策略，背叛總是最好的策略，所以背叛行為是Nash平衡，也是進化穩定的策略。這意味著合作行為成功地入侵一個背叛的種群幾乎是不可能的，即使是已經成為合作的種群，也很難抵制背叛個體的入侵。于是，合作進化對Allee效應的影響更加敏感，將Allee效應這一因素引入囚徒困境博弈是合理的,而且更具有現實意義。

通過平衡態分析與數值模擬發現，在Allee效應的影響下，分類相遇對合作進化仍然是必要條件。Allee效應導致合作行為與背叛行為構成的囚徒困境系統具有更多的平衡態，破壞原來的平衡，形成新的平衡態，并且最終平衡態值隨行為策略的初始斑塊占有率的變化而改變，這對合作進化的管理與保護具有重要的啟示意義。系統(1)研究結果表明，優越的外部環境有利于種群的發展，但卻抑制了合作行為的進化，相反，適當的環境壓力可以促進合作行為的空間入侵和維持。考慮了種群受Allee效應的影響之后，分析結果說明，在惡劣的環境條件下，Allee效應將導致物種滅絕，這也就意味著合作進化不復存在，而在相對優越的外部環境中，Allee效應的存在促進合作行為的進化，且隨著Allee效應強度的增強，更有利于合作行為的入侵，不過過強的Allee效應依舊會導致物種滅絕。因此，從保護生物學的角度來說，Allee效應對合作進化的影響是不容忽視的，尤其是瀕臨物種。應該采取相應的保護措施，例如，就地保護或遷地保護[20]等,這不僅能保護生物的多樣性，而且還可以有效地促進合作行為的進化。

參考文獻(References):

[1]Li Y, Lan X, Deng X Y, Sadiq R, Deng Y. Comprehensive consideration of strategy updating promotes cooperation in the prisoner′s dilemma game. Physica A: Statistical Mechanics and its Applications, 2014, 403: 284- 292.

[2]Allee W C. Animal Aggregations: A study in General Sociology. Chicago: University of Chicago Press, 1931.

[3]Courchamp F, Berec L, Gascoigne J. Allee Effects in Ecology and Conservation. Chicago: University of Chicago Press, 2008.

[4]Shi J P, Shivaji R. Persistence in reaction diffusion models with weak allee effect. Journal of Mathematical Biology, 2006, 52(6): 807- 829.

[5]Berec L, Angulo E, Courchamp F. Multiple allee effects and population management. Trends in Ecology & Evolution, 2007, 22(4): 185- 191.

[6]Pal P J, Saha T, Sen M, Banerjee M. A delayed predator-prey model with strong Allee effect in prey population growth. Nonlinear Dynamics, 2012, 68(1/2): 23- 42.

[7]Bai Z J, Yang W S, Li X P. Qualitative Analysis of a predator-prey system with Allee effect for prey. Annals of Differential Equations, 2007, 23(4): 386- 390.

[8]Aguirrea P, González-Olivaresb E, Sáeza E. Two limit cycles in aLeslie-Gowerpredator-prey model with additive Allee effect. Nonlinear Analysis: Real World Applications, 2009, 10(3): 1401- 1406.

[9]Wang W X, Zhang Y B, Liu C Z. Analysis of a discrete-time predator-prey system with Allee effect. Ecological Complexity, 2011, 8(1): 81- 85.

[10]Zhang F, Hui C. Eco-evolutionary feedback and the invasion of cooperation in prisoner′s dilemma games. PLoS One, 2011, 6(11): e27523.

[11]Eshel I, Cavalli-Sforza LL. Assortment of encounters and evolution of cooperativeness. Proceedings of the National Academy of Sciences of the United States of America, 1982, 79(4): 1331- 1335.

[12]林振山, 劉會玉, 劉紅玉. 人類活動影響下具有Allee 效應的非自治種群演化模式的研制及其應用——以丹頂鶴為例. 生態學報, 2005, 25(5): 945- 951.

[13]Hauert C, Szabo G. Game theory and physics. American Journal of Physics, 2005, 73(5): 405- 414.

[14]陳玲玲, 林振山. 非Allee與Allee競爭種群系統的動力學研究. 南京師范大學學報: 自然科學版, 2008, 31(2): 124- 129.

[15]González-Olivares E, Mena-Lorca J, Rojas-Palma A, Flores J D. Dynamical complexities in theLeslie-Gowerpredator-prey model as consequences of the Allee effect on prey. Applied Mathematical Modelling, 2011, 35(1): 366- 381.

[16]Ferdy J B, Austerlitz F, Moret J, Godelle P H, Godelle B. Pollinator-induced density dependence in deceptive species. Oikos, 1999, 87(3): 549- 560.

[17]Stoner A, Ray-Culp M. Evidence for Allee effects in an over-harvested marine gastropod: denity dependent mating and egg production. Marine Ecology Progress Series, 2000, 202: 297- 302.

[18]Kuussaari M, Saccheri I, Camara M, Hanski I. Allee effect and population dynamics in the Glanville fritillary butterfly. Oikos, 1998, 82(2): 384- 392.

[19]Courchamp F, Grenfell B, Clutton-Brock T. Impact of natural enemies on obligately cooperative breeders. Oikos, 2000, 91(2): 311- 322.

[20]安德烈·普林. 保護生物學. 賈競波, 譯. 北京: 高等教育出版社, 2005.

Cooperative evolution of a population with the Allee effect

ZHANG Ruiling1, WANG Wanxiong1,2,*, QIN Lijuan1,2

1CollegeofResourcesandEnvironmentalScience,GansuAgriculturalUniversity,Lanzhou730070,China

2CollegeofScience,GansuAgriculturalUniversity,Lanzhou730070,China

Abstract：It is well know that the prisoner′s dilemma game is a common phenomenon in ecology. Cooperator-defector interactions are ubiquitous in a population. One considered the ecological model was the cooperative evolution in the prisoner′s dilemma game without the Allee effect. However, the Allee effect is a crucial phenomenon that has drawn considerable attention from ecologists. It describes a positive interaction among individuals in low population sizes, and these interactions may be critical for survival and reproduction. The Allee effect can be caused by any number of factors, for example, finding mates between the individuals of a species in low population densities, reduced defense against predators, special trends of social dysfunction, etc. Meanwhile, the Allee effect is a destabilizing factor in species persistence in the evolvement, and largely increases the possibility of the species′ local extinction, even its global extinction. Many species, especially the endangered species, are more susceptible to the influlence of the Allee effect. Therefore, it is important to study cooperative evolution in a population with the Allee effect. Based on the system described by Feng Zhang & Cang Hui, we formulated a new prisoner′s dilemma game model, in which the population was subjected to the Allee effect. Theoretical analysis and numerical simulation were used to investigate how the Allee effect influences cooperative evolution. The results show that, the assortment is still a necessary condition for the evolution of cooperation in the ecological context, and cooperative evolution becomes easier under density-dependent selection. At the same time, our study also indicates that the Allee effect can easily lead to the extinction of species, and acts against cooperative evolution under unfavorable environmental conditions. However, in the relatively superior environmental conditions (causing low death rate), the rise of cooperation could be much easier due to the Allee effect. As the Allee effect becomes stronger, it promotes more favorable cooperative evolution. However, the occupancy of a population will decrease as the strength of the Allee effect increases in the spatial pattern. When the value of the Allee effect is greater than the threshold value, the population eventually tends to become extinct.

Key Words:allee effect; prisoner′s dilemma game; cooperation strategy; death rate

DOI:10.5846/stxb201407261515

*通訊作者Corresponding author.E-mail: wangwx@gsau.edu.cn

收稿日期:2014- 07- 26; 網絡出版日期:2015- 07- 27

基金項目:國家支撐計劃(2007BAD88B07)；國家自然科學基金資助項目(31260098，31360148)；甘肅省自然科學基金資助項目(1208RJYA037)

張瑞玲，王萬雄，秦麗娟.具有Allee效應的合作進化.生態學報,2016,36(1):261- 267.

Zhang R L, Wang W X, Qin L J.Cooperative evolution of a population with the Allee effect.Acta Ecologica Sinica,2016,36(1):261- 267.