數學之“美”

古希臘偉大的哲學家亞里士多德早就指出:“認為數學的科學全不涉及美或善是錯誤的……數學的科學特別體現秩序、對稱和明確性,而這些正是美的主要形式。”筆者認為數學中的美感俯拾即是,在解題教學中,可嘗試對學生進行數學美的熏陶。
一、簡潔美
愛因斯坦說過:“美,本質上終究是簡單性。”他還認為,只有借助數學,才能達到簡單性的美學準則。數學解題中的“簡潔美”有很多,以下僅舉一例。
運用整體思想,且用字母代替原題中的兩個式子,復雜的計算問題解決得簡潔而明快,充分體現了數學問題解決中的“簡潔美”。其實,數學中最為簡潔的美莫過于歐拉公式V-E+F=2,頂點數V,棱數E,面數F,如此簡單的一個公式,不計其數的多面體,都必須服從它。需要說明的是數學語言本身和數學中的許多公式和定理本身就體現了“簡潔美”。
二、異曲同工美
數學中的許多問題可以用不同的方法去解決,最后得到的結果無論在形式上和實質上都是一致的,體現了數學本身的內在統一,可謂“異曲同工”。
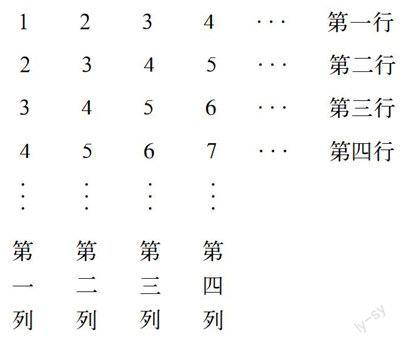
根據表中所反映的規律,猜想第n行(n為正整數)與第n列的交叉點上的數應為 ? ? ? ? ? ? ? 。
【方法一】先考察特殊的情形第一行第一列交叉處的數為1,第二行第二列交叉處的數為3,第三行第三列交叉處的數為5,第四行第四列交叉處的數為7,根據此規律這一串數為1,3,5,7…所以第n行第n列交叉處的數為2n-1。
【方法二】考察行列交叉處的數與行數和列數的關系,這個數等于行數與列數的和減去一。例如,第3行第3列交叉處的數為5=3+3-1,所以第n行第n列交叉處的數為n+n-1=2n-1。
實際上方法一中的每行每列交叉處的數都可以寫成方法二中的形式,兩種不同的方法結果一致,可謂“殊途同歸”。
三、和諧美
我國著名的數學家華羅庚曾說過,“數缺形時少直觀,形少數時難如微;數形結合百般好,隔離分家萬事休”。數學中數和形是兩個最主要的研究對象,它們之間有著十分密切的聯系,在一定的條件下,數和形之間可以相互轉化,相互滲透。
【例3】,求1+2+3+…+n的值,其中n為正整數。對于這個求和問題,如果采用純代數的方法(首尾兩頭加),問題雖然解決了,但在求和的過程中,需對n的奇偶性進行討論。
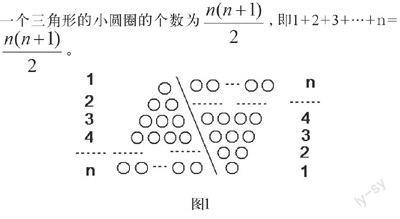
如果采用數形結合的方法,即用圖形的性質來說明數量關系的事實,那會非常直觀。現利用圖形的性質來求1+2+3+…+n的值,方案如下:如圖1,斜線左邊的三角形圖案是由上到下每層依次分別為1,2,3,…,n個小圓圈排列組成的。而組成整個三角形的小圓圈的個數恰好為1+2+3+…+n的值,現把左邊三角形倒放于斜線的右邊,與原三角形組成一個平行四邊形。此時組成平行四邊形的小圓圈共有n行,每行有(n+1)個小圓圈,所以組成平行四邊形小圓圈的總個數為n(n+1)個,因此,組成一個三角形的小圓圈的個數為,即1+2+3+…+n= ? ?。
(1)仿照上述數形結合的方法,設計相關圖形,求1+3+5+…+(2n-1)的值,其中n為正整數。(要求:畫出圖形,并利用圖形做必要的推理說明)
(2)試設計另外一種圖形,求1+3+5+…+(2n-1)的值,其中n為正整數。(要求:畫出圖形,并利用圖形做必要的推理說明)
【解析】其中(1)的做法和原題中的方法相類似,這里不再贅述,第(2)小題可畫出如圖2的圖形,第一個直角中有1個小圓圈,第二個直角中有3個小圓圈,第三個直角中有5個小圓圈……第n個直角中有(2n-1)個小圓圈,組成整個正方形的小圓圈的個數恰好為1+3+5+…+(2n-1)的值,另一方面正方形每行有n個小圓圈,共有n行,所以小圓圈的總數為n2個,即1+3+5+…+(2n-1)= n2。
這個問題中數和形是如此的和諧統一,不得不令人驚嘆,在解題中我們深刻感受到了數學的美輪美奐。
四、奇異美
解題中的奇異美是指題中得出的結論或解題方法出人意料,讓人感到詫異和驚奇。例如,最近幾年中考試題中經常出現的七巧板拼圖問題,讓學生盡情領略到數學的奇異之美。用七塊板可以拼成一個最簡單的正方形,也可以拼出千變萬化的復雜圖案,如人形、鳥獸、花草、房屋等。學生所能拼出的圖案之多之美,出人意料。數學題有一般的規律和一般的解題模式,但每道數學題也都有各自特殊的性質,這些特殊的性質構成了數學的奇異美,根據數學的奇異美。在求解某些數學問題時,要打破常規,突破現成的思維模式,找到別開生面、出奇制勝的解法。
總之,教師在解題教學中若能把數學問題中這些美學本質挖掘出來,必能提高學生學習數學的興趣,激發學生對數學美的體驗,啟迪學生的思維,開拓學生的視野。因此在解題教學中對學生進行美的熏陶值得一試。
周凌峰,男,周莊中學校長、黨支部書記,曾在2011年8月受教育局指派,赴山西省呂梁市離石區支教。榮獲“江陰市青年教師教學大比武一等獎”“江陰市優秀共產黨員”“江陰市優秀班主任”“江陰市教學能手”“江陰市優秀教育工作者”“離石區優秀班主任”“呂梁市離石區五一勞動獎章”“無錫市青年教師評優課一等獎”“無錫市優秀教育工作者”“無錫市教學能手”“感動山西特別獎”等稱號。
教科研方面注重實效,參與編輯《初中數學知識表解》一書,參與國家級重點課題“創新型教師培養”、江蘇省重點課題“構造積極心理場”,獨立主持無錫市教師專項課題“概念圖在數學教學中的應用”。《求導誠可貴,構造價更高》《例談數學教材中的例題和習題教學》《追求“我”的課堂》《探索向量問題求解 彰顯數學思想魅力》等論文發表于《理科考試研究》等雜志,并有多篇文章在全國、無錫市、江陰市各類評比中獲一、二等獎。

