光學遙感衛星對月定標時姿態機動補償方法

高涵 白照廣 陸春玲 邸國棟

(航天東方紅衛星有限公司，北京 100094)

光學遙感衛星對月定標時姿態機動補償方法

高涵 白照廣 陸春玲 邸國棟

(航天東方紅衛星有限公司，北京 100094)

對月定標具有不依賴地面定標場、不受天氣影響、定標效率高等優勢，但需要解決對月姿態控制及成像參數匹配性設計問題。文章針對光學遙感衛星推掃成像，提出一種姿態機動補償方法，用于解決星載相機對月成像過程中積分時間與推掃速度失配的問題，并以一顆太陽同步軌道衛星作為分析對象，研究了衛星對月成像時的補償角速度，經過對姿態機動補償過程進行仿真分析，結果表明：使用該方法可以使相機推掃速度與積分時間匹配，達到正常對月成像的目的。

時間延遲積分CCD；對月成像；姿態機動補償

1 引言

衛星發射前后，為獲取精確的星上遙感器輻射特性和輻射響應變化，需要對星上的敏感器件進行輻射定標工作。我國遙感衛星的在軌定標目前仍以地球表面真實景物目標為主，精度受大氣環境影響較大，定標頻次較低。利用空間天體進行在軌輻射定標可以消除大氣層影響，提高定標頻次。在天體定標中，對日定標有比較廣泛的應用；但由于太陽光太強，超出遙感器動態范圍，需要采用漫射板反射太陽光線，而漫散板長期暴露在宇宙空間輻射中，極易受到污染，引起性能退化，不適于長壽命遙感衛星。天體定標方法中，對月定標成為國際上研究的熱門。

月球是除太陽外所能觀察到的最大的光源，依靠反射太陽而發光，其光譜特性與太陽光譜的自身吸收、反射有關，穩定性好，且光強一般在遙感器動態范圍內，可將遙感器直接對月成像。采取對月成像的方式，可以對衛星大部分光學遙感儀器定標，在獲取標準月球輻照度模型的情況下(如美國的ROLO模型)，利用月球進行絕對輻射定標需要精確地計算出觀測角度和天體距離等的影響，并獲取準確的月球光譜分布，可實現高定標精度，適合長壽命遙感衛星。

對月定標不受大氣影響，在地影區進行成像，不影響陸地成像，可增加定標次數。將月球作為穩定輻射源，定標時機的選擇與相機本身參數和月相有關，定標時間選擇范圍增加，可以提高定標頻率和定標精度，拓寬定標時機的選擇面。

目前，遙感衛星對月成像方式為：通過控制衛星的初始姿態角實現相機光軸對月球定向后，利用衛星繞地球軌道的運動實現對月絕對定標成像，在定標過程中，衛星整星姿態不采取修正措施。獲取的月球圖像模糊不清，甚至無法辨識。產生模糊的原因是相機的積分時間與光軸在月球表面的推掃速度失配引起的過采樣[1-4]。過采樣情況下相機光生電荷無法正常讀出，成像調制傳遞函數(MTF)將下降，直接造成對月定標精度降低。因此過采樣問題是對月定標過程須解決的首要難題。

目前，解決過采樣問題有兩種方法：第一種針對早期的線陣CCD相機，采用地面數據處理的方式還原畸變圖像[5]；第二種針對高精度的TDICCD相機，采用技術或設備使得相機積分時間寬幅可調。文獻[6]中的中分辨率光譜成像儀(MODIS)遙感器就是采用地面數據處理的方式還原畸變圖像；文獻[7]敘述了我國風云二號衛星利用月球進行內黑體定標的過程，星上可見光-紅外自旋掃描輻射計(VISSR)遙感器與MODIS類似，也通過地面數據處理對畸變圖像進行配準補償；文獻[8]中的昴宿星(Pleiades)衛星，使用TDICCD相機對月成像，該相機具有較大的積分時間可調范圍(0.3～3 ms)。上述兩種方法適用性單一，且存在一定缺陷或難度：采用地面處理的方式只能還原普通線陣CCD相機的畸變圖像，會造成圖像精度降低，影響定標精度，且該方法對于TDICCD相機并不適用；增加積分時間可調范圍的方法可以有效解決TDICCD相機對月定標的過采樣問題，但需要兼顧曝光量的飽和值與相機信噪比的關系，對設備的性能要求較高，同時該方法不能夠用于普通線陣CCD相機。

本文針對上述問題，提出采用姿態機動補償TDICCD相機推掃速度的方法，在不額外增加儀器、不改變原有掃描行周期的情況下，僅通過對衛星姿態角速度的控制增加衛星推掃速度，使得推掃速度與積分時間匹配，完成對月定標工作。此方法不但可以用于TDICCD相機，對于普通線陣CCD相機同樣適用。

2 衛星姿態機動補償方法

2.1 成像方式分析與補償角速度分析

衛星對月成像過程中，相機光軸需要對月球慣性定向，進而對月球推掃成像。TDICCD相機成像時需要沿積分方向推掃[9]。由于衛星距月球較遠，衛星對月成像時間很短，在成像過程中可以假設月球靜止，同時令衛星的偏航角始終保持為零。根據上述特性及分析結果，提出兩種成像方式：第一，衛星先進行滾轉機動，相機光軸由指向地面轉到指向空間，再通過俯仰機動，令光軸對月球定向，見圖1，此時相機光軸推掃方向與衛星沿軌道運動方向相同；第二，衛星先進行俯仰機動，相機光軸由指向地面轉到指向空間，再進行滾轉機動，使光軸對準月球，見圖2，此時相機光軸推掃方向與衛星沿軌道運動方向相反。兩種機動方式中，相機推掃成像方向與衛星沿軌道運動方向的差異會引起對月推掃補償角速度的差異。

圖1 采用第一種方式成像(推掃方向與運動方向相同)Fig.1 Lunar imaging using the first method (scanning direction is the same as motion direction)

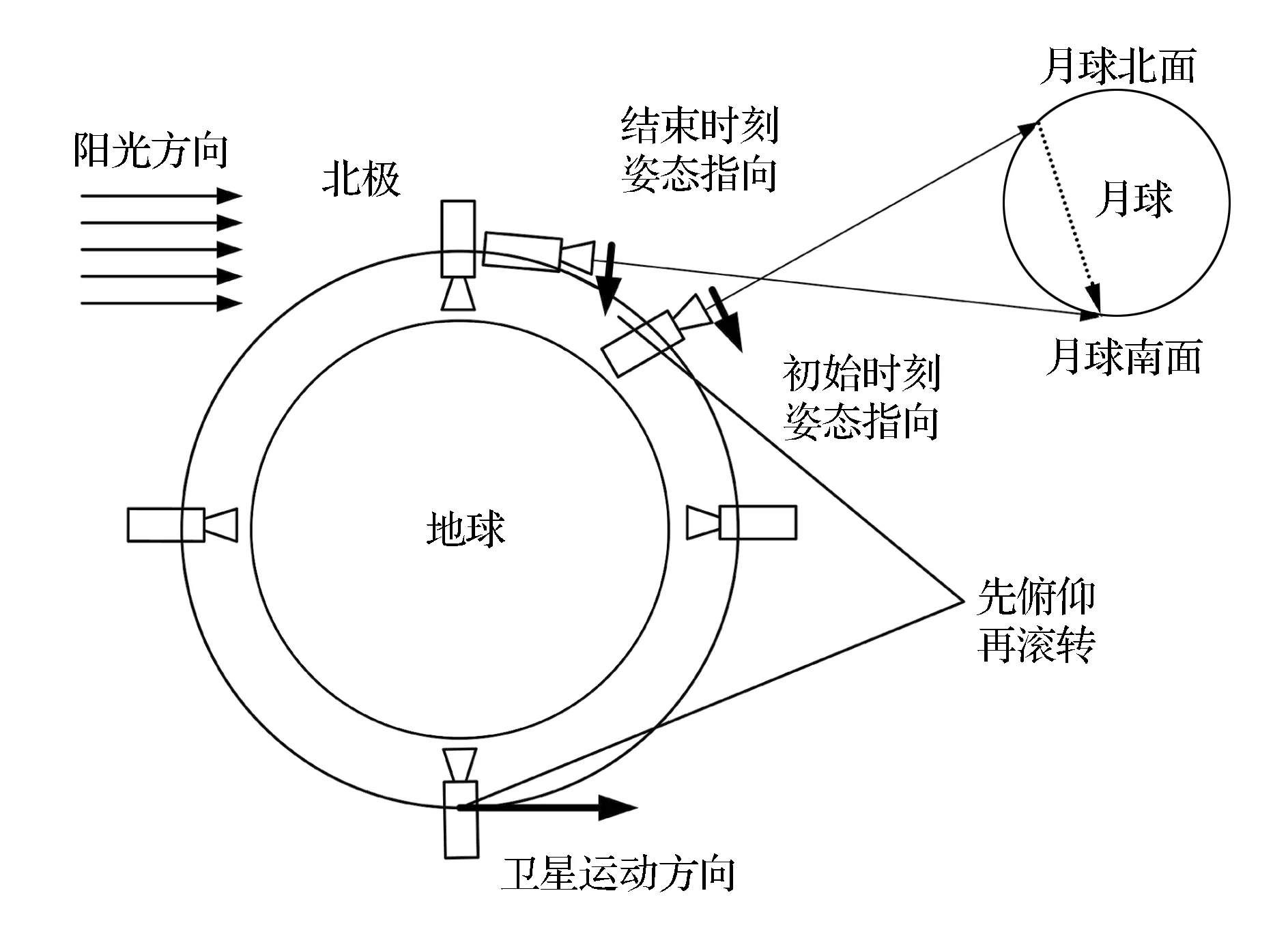
圖2 采用第二種方式成像(推掃方向與 運動方向相反)Fig.2 Lunar imaging using the second method (scanning direction is opposite to motion direction)

使用兩種不同的成像方式，衛星繞地球運動實現對月成像，成像方向與對地成像相同，與衛星滾動軸同向，與俯仰軸垂直，如圖3所示，此時衛星視軸推掃速度過慢，景物不能按正確的行周期進入下一級敏感單元，引起多幀圖景的重疊覆蓋，即過采樣情況；如果保證偏航角不變，對衛星施加俯仰機動，如圖4所示進行俯仰機動補償后，衛星推掃速度加快，景物可以依次進入下一級敏感單元，即利用衛星繞俯仰軸的姿態機動達到補償推掃速度的目的，令相機積分時間與光軸在月球表面的推掃速度匹配，從而解決過采樣問題。

使用姿態機動的方法對推掃速度進行補償時，須要計算補償角速度和成像時刻衛星姿態角，補償角速度通過衛星軌道參數和成像參數計算；成像時刻姿態角須要建立衛星姿態運動學模型求取，因此要根據衛星本身的成像特性對補償情況進行分析計算。首先計算衛星軌道參數和成像參數[10]。

衛星的星下點地速為

(1)

地面采樣距離為

(2)

積分時間為

(3)

式中：Vn是星下點地速，R=6 371.004 km，a是軌道半長軸，μ為地球引力常數，DGSD為地面采樣距離，H為軌道高度，d為像元尺寸，f′為相機焦距。

由于衛星和月球距離較遠，忽略衛星在軌運動時衛星和月球間的距離變化，取衛星處于地月連線附近時衛星和月表之間的距離作為定標時的距離，根據衛星成像參數與軌道參數，計算得到補償俯仰角速度為

(4)

式中：S表示地月距離，Rm為月球半徑，V是與積分時間相匹配的推掃速度，v是衛星在軌運行時光軸在月球表面的投影線速度。當衛星采用第一種方式對月成像時，式(4)中取減號；采用第二種方式對月成像時，式(4)中取加號。

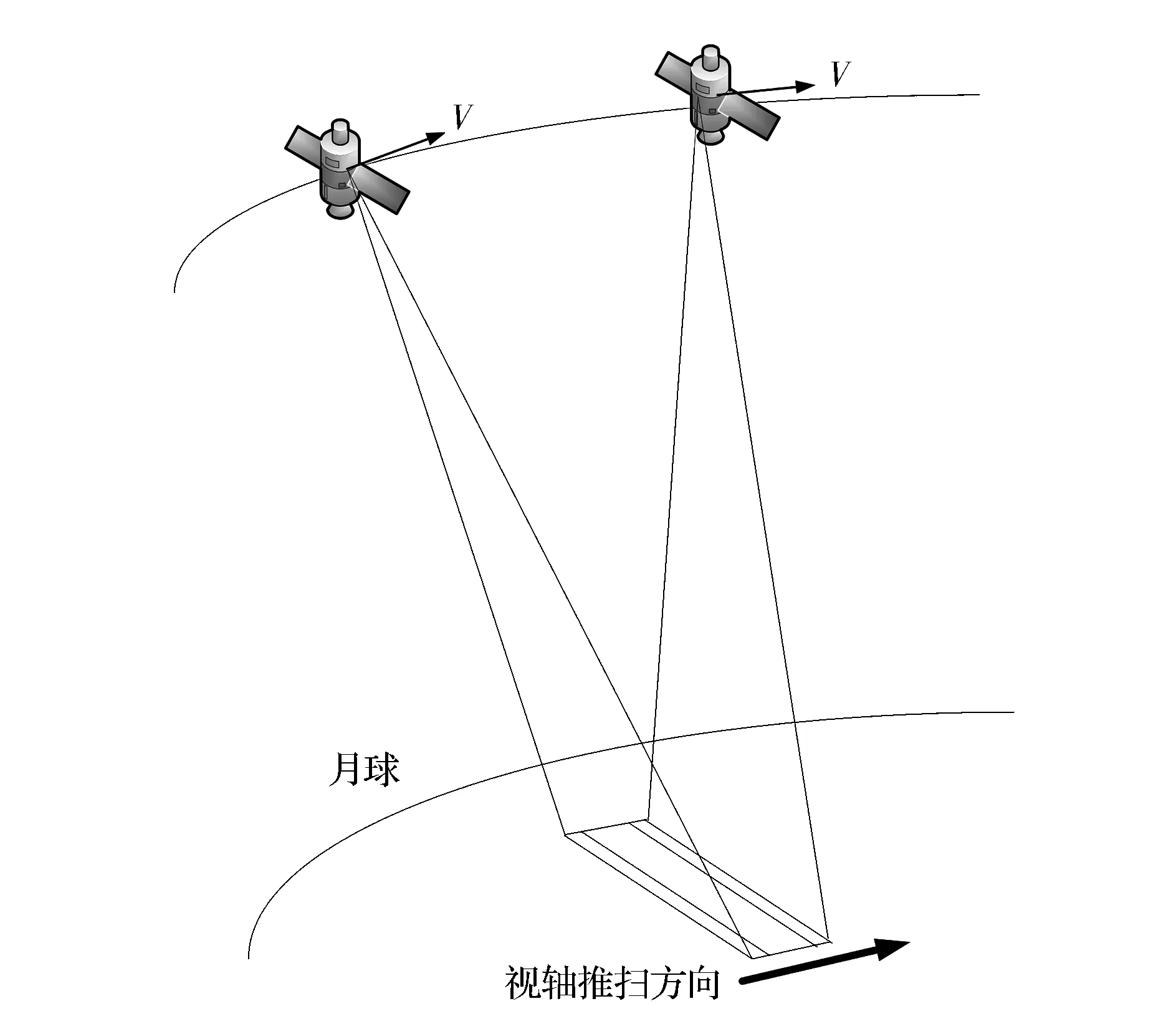
圖3 姿態機動補償前衛星對月成像圖示Fig.3 Lunar imaging without the attitude maneuver compensation

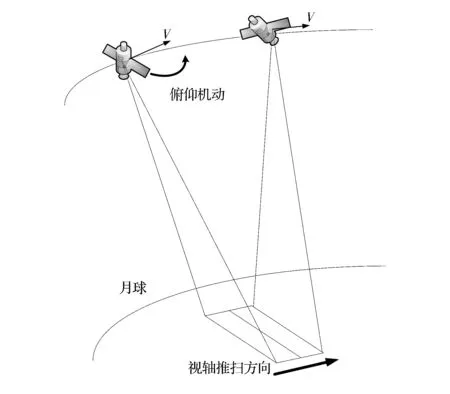
圖4 姿態機動補償后衛星對月成像圖示Fig.4 Lunar imaging with the attitude maneuver compensation

2.2 衛星姿態運動學建模

已知衛星的補償角速度，根據衛星對月成像方式建立衛星姿態運動學模型，求取衛星對月定標各個時刻的姿態，選取不同時刻的姿態進行機動補償。建立如圖5中成像幾何模型，引入如下坐標系。

(1)地心慣性坐標系Oi-XiYiZi：即地心赤道慣性系，其原點O在地心，Xi軸指向春分點，Zi軸垂直于赤道面指向北極，Yi軸由右手法則確定。

(2)衛星軌道坐標系Oo-XoYoZo：也稱為相對運動坐標系，其原點Oo在航天器質心，Xo軸指向航天器前進方向，Zo由航天器質心指向地心，Yo軸垂直于Xo和Zo構成的軌道平面，按右手法則確定。

(3)衛星本體坐標系Ob-XbYbZb：原點Ob在衛星質心，Xb，Yb，Zb三個坐標軸固定在航天器本體上，三個坐標軸和星體主慣量軸一致。

下面是三個坐標系之間相互轉換關系：

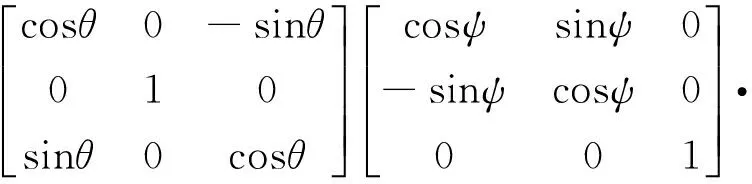
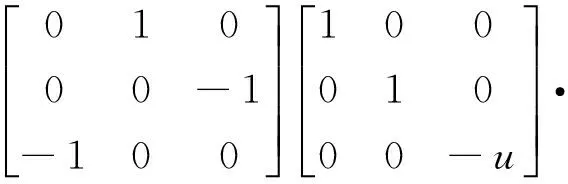
(5)

式中：Cbo表示衛星軌道坐標系到衛星本體坐標系的轉換關系，Coi表示慣性系到衛星軌道坐標系的轉換關系。R為地球半徑，H為衛星軌道高度，i0為軌道傾角，u表示緯度幅角，u=w+f，w為近地點幅角，f為真近點角，其中Ω為衛星軌道的升交點赤經；ψ，φ，θ表示成像時偏航、俯仰和滾轉角。

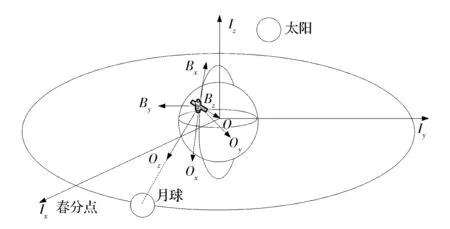
圖5 對月成像幾何模型Fig.5 Lunar imaging geometric model

預先給定衛星每次成像的起始時間，計算衛星每次成像開始時的姿態角，方法如下：在地心慣性坐標系Oi-XiYiZi中，根據衛星軌道和月球星歷確定每次成像的成像衛星與月球之間的位置矢量p，p即衛星本體坐標系Zb的指向，將慣性坐標系中的位置矢量p轉換到衛星本體坐標系Ob-XbYbZb中，在三軸進行投影得到p=[p1p2p3]T。

月球星歷采用JPL星歷表，JPL星歷表是由美國噴氣推進實驗室(JPL)依據最新確定的天文常數和天體運動理論計算的各大行星、太陽、地球及月球的相對位置、速度、黃經章動和月球物理天平動及其變率的數值[11]。根據角度關系求得任意成像開始時刻的衛星姿態角如下。

(6)

(7)

ψ=0°

(8)

3 仿真分析

圖6 姿態機動補償建模與仿真流程圖Fig.6 Flow chart of modeling and simulation for attitude maneuver compensation

3.1 衛星補償角速度仿真分析

為了驗證姿態補償效果，仿真過程中使用Matlab軟件和STK軟件，通過Matlab軟件獲取仿真數據，并進行數據分析；利用Matlab軟件控制STK軟件進行交互，直觀觀察補償過程。設衛星軌道高度為650 km，TDICCD相機像元尺寸d=8.75 um，焦距f′=2850 mm。根據式(1)～(3)計算得到，衛星星下點地速為Vn=6.845 km/s，地面像元投影尺寸DGSD=2 m，積分時間Tint=0.289ms。仿真結果中x軸和y軸分別為衛星運行時間和衛星與月球距離，衛星從南極到北極半圈軌道的運行時間0～3000s，衛星與月球距離按照星歷輸入。

通過圖7～圖10可以看出：

(1)衛星在無補償的情況下，各個時刻光軸在月球表面投影線速度隨星月距離和衛星運行時間的變化而變化，設沿衛星運動方向推掃時速度為正，該數值-37.2km/s～442.7km/s，見圖7。產生負值的原因是由于黃白交角的存在。

(2)如圖8和圖9所示，衛星采用兩種不同的成像方式時， 補償角速度從兩極到赤道的變化規律正好相反，在赤道和兩極附近分別取得最大或最小值，因此在進行任務規劃時，可以根據該變化規律選擇補償角速度最小的位置進行定標，從而節省機動時間。兩種成像方式下，衛星的補償角速度變化范圍分別為0.505 1(°)/s～0.667 5(°)/s(第一種)和0.557 2(°)/s～0.728 8(°)/s(第二種)，從補償角速度的大小來考慮，第一種成像方式需要的補償角速度較小，對姿態控制要求較低，更適合進行對月成像工作。

(3)姿態機動補償前后光軸在月表投影線速度存在較大差異，見圖10，黑色和白色曲面分別代表姿態機動補償前后衛星遙感器光軸在月表投影線速度隨星月距離和時間的變化關系，補償后的線速度從3 726.9km/s～4 389.6km/s，是補償前線速度-37.2km/s～442.7km/s的近10倍。

圖7 衛星無補償時光軸在月表投影線速度 隨星月距離和時間變化關系示意圖Fig.7 Projection linear speed of optical axis on moon versus time and the distance between satellite and the moon without compensation

圖8 采用第一種成像方式的補償角速度 隨星月距離和時間變化關系示意圖Fig.8 Compensation angular velocity for lunar imaging versus time and the distance between satellite and the moon using the first imaging method

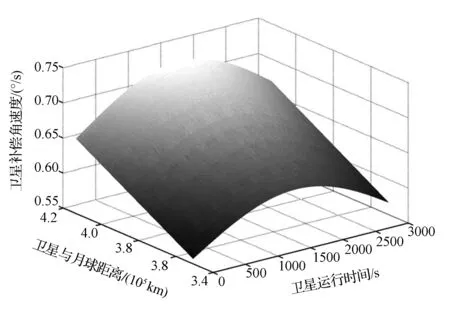
圖9 采用第二種成像方式的補償角速度隨 星月距離和時間變化關系示意圖Fig.9 Compensation angular velocity for lunar imaging versus time and the distance between satellite and the moon using the second imaging method

圖10 補償前后衛星遙感器光軸在月表投影線 速度隨星月距離和時間變化關系的對比圖Fig.10 Comparison of projection linear speed of optical axis on moon versus time and distance between satellite and the moon before and after compensation

3.2 補償過程姿態角仿真分析

按照月球接近滿月時，選取仿真時刻2018-03-29T10：11：30.000，分別采用兩種成像方式成像，下面是采用兩種成像方式成像時，姿態機動補償前后衛星姿態角變化情況。

從圖11～圖14可以看出：

(1)對月成像過程時間較短，整個過程用時約1 s，因此設月球在定標期間位置保持相對靜止符合實際情況，在對月定標過程中預設偏航角保持不變，始終為0°，成像過程中只補償俯仰角，因此滾動角也不發生變化。

(2)衛星采用第一種成像方式，未補償前在成像時間內，俯仰角10.51°～10.56°(見圖11)，衛星視場從月球邊緣向中心沿積分方向推掃0.054°，補償后俯仰角10.51°～10.01°(見圖12)，衛星視場從月球邊緣向中心沿積分方向推掃0.52°；采用第二種成像方式，未補償前在成像時間內，俯仰角168.99°～168.94°(見圖13)，衛星逆積分方向推掃0.051°，補償后俯仰角從168.99(°)/s～169.51(°)/s(見圖14)，衛星沿積分方向推掃0.53°；在不采用姿態機動補償的情況下，第二種成像方式根本無法成像。

(3)采用第一種成像方式時，衛星定標時姿態角為[0° 10.51° 174.34°]，采用第二種成像方式時為[0° 168.45° 20.18°]，從達到預定姿態角的總機動角度來考慮，應選取總機動角度較小的第一種成像方式，而從補償角度考慮也應該選擇補償角速度較小的第一種成像方式。

圖11 采用第一種成像方式未進行姿態機動 補償時的姿態角變化Fig.11 Changes of attitude angle versus time using the first imaging method without attitude maneuver compensation

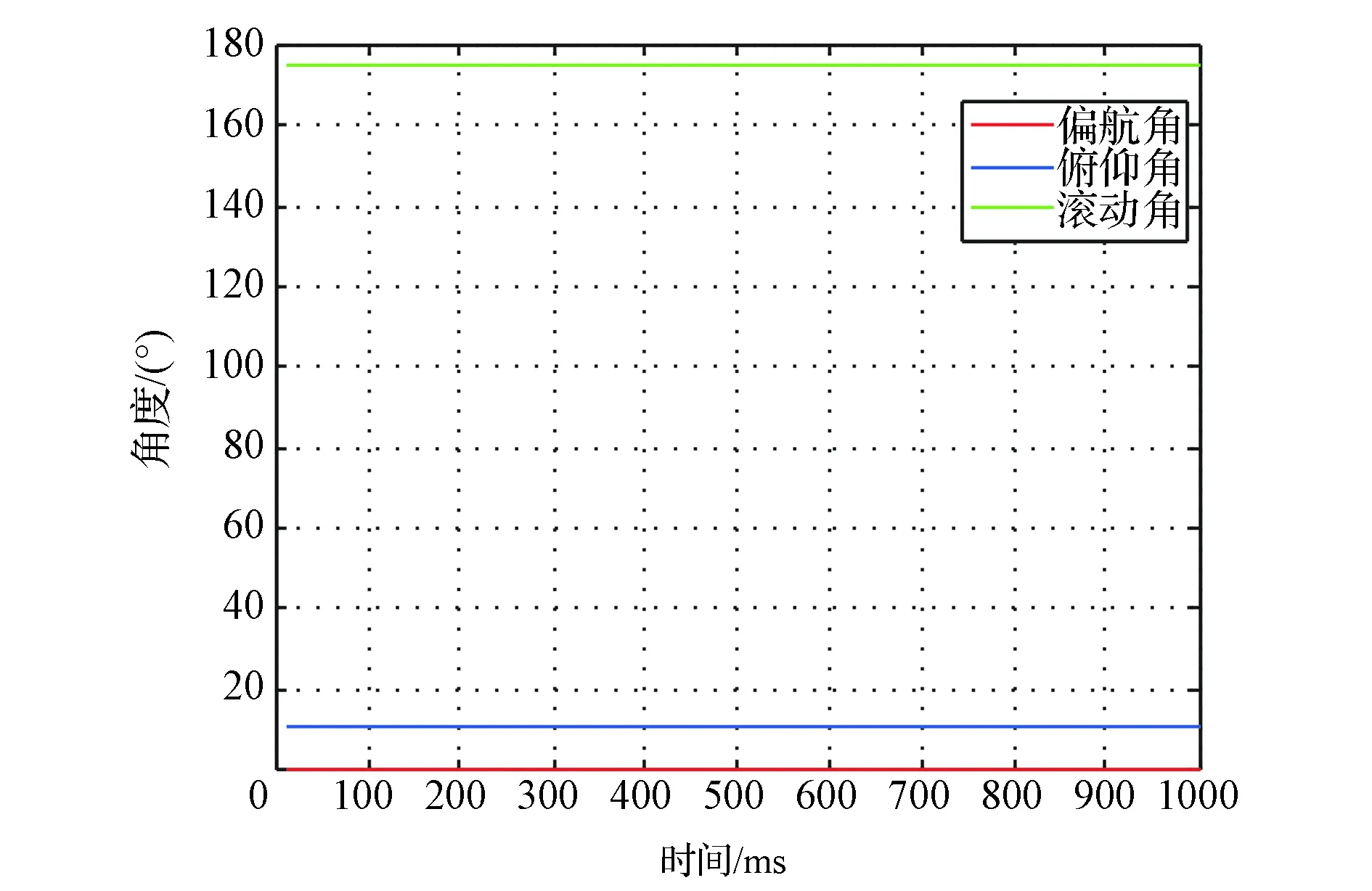
圖12 采用第一種成像方式進行姿態機動 補償后的姿態角變化Fig.12 Changes of attitude angle versus time using the first imaging method with attitude maneuver compensation

圖13 采用第二種成像方式未進行姿態機動 補償時的姿態角變化Fig.13 Changes of attitude angle versus time using the second imaging method without attitude maneuver compensation

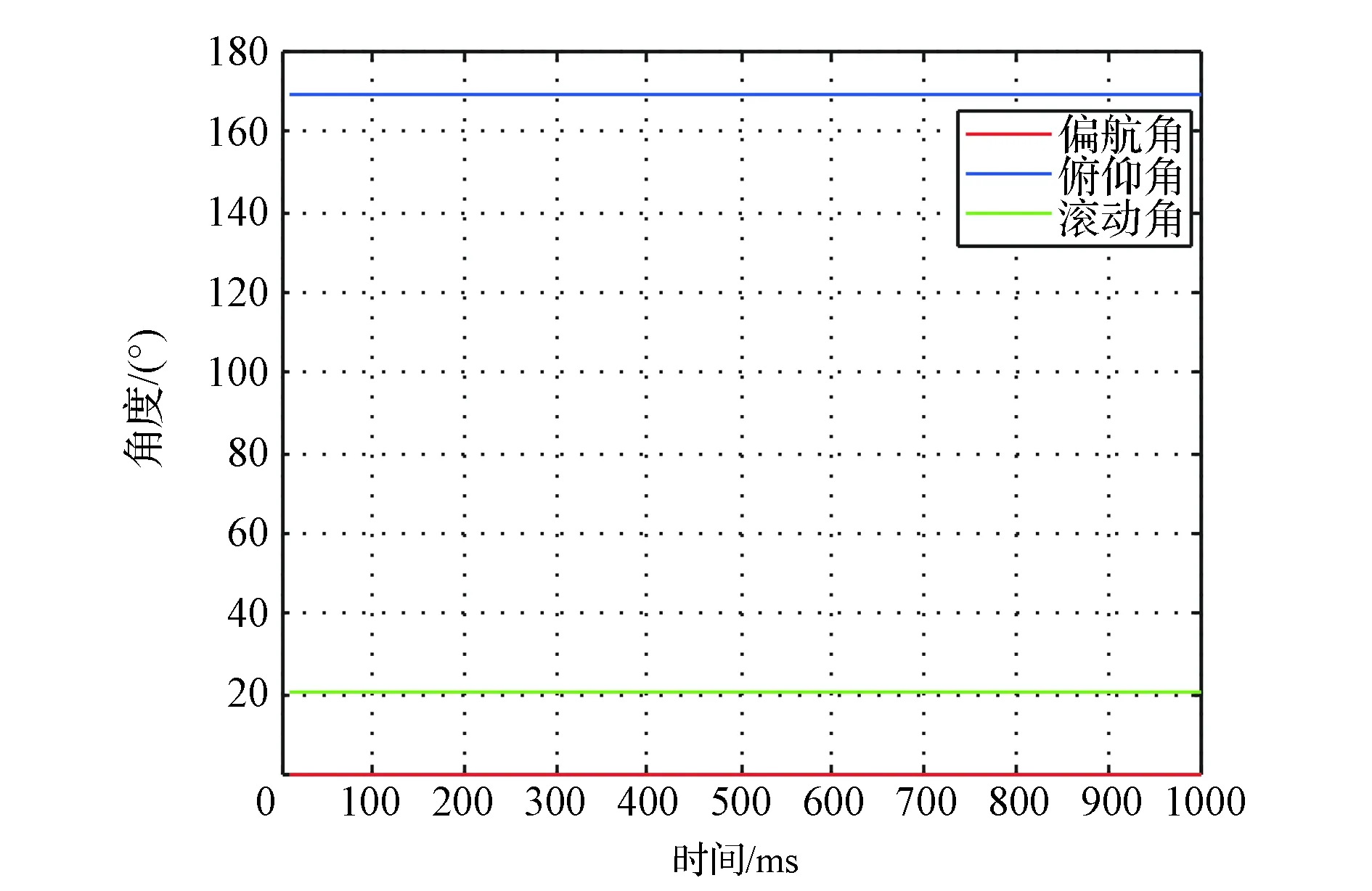
圖14 采用第二種成像方式進行姿態機動 補償后的姿態角變化Fig.14 Changes of attitude angle versus time using the second imaging method with attitude maneuver compensation

3.3 衛星場景仿真

為了更好地模擬真實遙感衛星成像特點，在STK中建立仿真場景，選擇650 km太陽同步軌道衛星(見圖15)，選取一般國內遙感衛星可見光成像時間較好的10:30作為降交點地方時，星上安裝一臺CCD相機，衛星具有側擺能力，視場角為8.6°，焦距2850 mm，選取滿月時刻進行對月定標仿真，選取仿真時刻為2018-03-29T10:11:30.000。將3.1節和3.2節中計算結果作為衛星姿態輸入參數；采用第一種成像方式時，衛星成像時刻姿態角為[0° 10.51° 174.34°]，補償俯仰角速度為dθ1=0.546 1(°)/s；采用第二種成像方式時，衛星姿態角為[0° 168.45° 20.18°]，補償俯仰角速度為dθ2=0.694 5(°)/s。

圖15 650 km太陽同步軌道衛星對月定標仿真過程Fig.15 Simulation scenario of satellite lunar calibration in 650km SSO

仿真結果顯示：衛星按照上述兩種方式對月成像，成像時間分別為t1=0.805 5 s和t2=0.803 8s，與理論計算值的標準推掃時間t=0.804 6s的偏差分別為0.11%和0.10%，可以達到正常成像的理論推掃速度，誤差主要來源于月球邊緣確定誤差和軟件本身舍入誤差。

4 結束語

對月定標以其高精度、高頻次和簡單易行的特點，將成為新一代衛星在軌定標的重要方式。為解決對月定標過程中積分時間與推掃速度相失配問題，本文提出了姿態機動補償方法，在不額外增加儀器、不改變原有掃描行周期的情況下，解決上述問題。針對兩種不同的對月成像方式使用姿態機動補償方法，最后對該補償方法進行了仿真驗證，仿真結果顯示：在兩種成像方式下，該姿態機動補償方法都可以實現推掃速度的補償，使TDICCD相機達到正常對月成像的推掃速度，解決過采樣問題，由于該方法具有不改變原有行周期的特性，因此也適用于積分時間固定的普通線陣CCD相機；該方法僅依靠衛星姿態機動實現補償，比較容易做到，因此可用于各種軌道高度上的光學遙感衛星的對月定標工作，提高定標頻次和定標精度。仿真結果中得到的兩種成像方式的補償特點和補償角速度隨時間和星月距離變化的規律，可以用于定標任務總體規劃以及定標具體時機的確定，對衛星總體設計和任務規劃具有參考意義。

)

[1] 陳福春,陳桂林,王淦泉.衛星遙感儀器的可見光星上定標[J].海洋科學進展，2004，22(z1)：34-38

ChenFuchun，ChenGuilin，WangGanquan.On-orbitvisiblecalibrationforsatelliteremotesensinginstrument[J].AdvancesinMarineScience，2004，22(z1)：34-38 (inChinese)

[2]朱興鴻,王瑞,白照廣.遙感衛星全視場成像質量仿真方法研究[J].航天器工程，2013，22(6)：11-17

ZhuXinghong，WangRui，BaiZhaoguang.Simulationmethodanalysisonfull-viewimagingqualityforremotesensingsatellite[J].SpacecraftEngineering，2013，22(6)：11-17 (inChinese)

[3]樊超,李英才,易紅偉.速高比對TDICCD相機的影響分析[J].兵工學報，2007，28(7)：817-821

FanChao，LiYingcai，YiHongwei.Influenceofvelocity-heightratioofsatelliteontheTDICCDcamera[J].ActaArmamentarii，2007，28(7)：817-821 (inChinese)

[4]JiaguWu，ZZHF.RestorationofTDIcameraimageswithmotiondistortionandblur[J].OpticsandLaserTechnology，2010，42(8)：1198-1203

[5]JoeSteyn，GeorgeTyc，KeithBeckett，etal.Rapideyeconstellationrelativeradiometricaccuracymeasurementusinglunarimages[C]//Sensors，Systems，andNext-GenerationSatellitesXIII.Bellingham：SPIE，2009：74740Y1-12

[6]SunJunqiang，XiongXiaoxiong，WilliamLBarnes,etal.MODISreflectivesolarbandson-orbitlunarcalibration[C]//IEEETransactionsonGeoscienceandRemoteSensing.NewYork:IEEE,2007:2383-2393

[7]LLebegue.UsingExoticguidanceforpleiades-hrimagequalitycalibration[C]//The21stISPRS.ChristianHeipke,Germany:ISPRS,2008:13-18

[8]郭強，陳博洋，張勇,等.風云二號衛星在軌輻射定標技術進展[J].氣象科技進展,2013(6):6-12

GuoQiang，ChenBoyang，ZhangYong,etal.Progressinon-orbitradiometriccalibrationtechnologyforFengyun-2satellite[J].AdvancesinMeteorologicalScienceandTechnology,2013(6):6-12 (inChinese)

[9]楊秉新.TDICCD在航天遙感器中的應用[J].航天返回與遙感,1997，18(3)：15-18

YangBingxin.ApplicationsofTDICCDinspaceremotesensors[J].SpacecraftRecovery&RemoteSensing，1997，18(3)：15-18 (inChinese)

[10] 任建岳,何斌,王家騏,等.航天光學遙感器像移速度矢計算數學模型[J].光學學報,2004，24(12):1585-1589

Ren Jianyue,He Bin,Wang Jiaqi，et al.Space optical remote sensor image motion velocity vector computational modeling[J].Acta Optica Sinica，2004，24(12):1585-1589 (in Chinese)

[11]馬高峰,魯強,鄭勇.JPL行星/月球星歷[C]//中國宇航學會深空探測技術專業委員會第一屆會議.北京：北京空間飛行器總體設計部,2005:395-401

Ma Gaofeng,Lu Qiang，Zheng Yong.Ephemeris of moon and planet by JPL[C]//The 1stConference for Deep Space Exploration Technology Committee of Chinese Society of Astronautics.Beijing:Beijing Institute of Spacecraft System Engineering,2005:395-401 (in Chinese)

(編輯：李多)

Attitude Maneuver Compensation Method on Lunar Imaging for Optical Remote Sensing Satellite

GAO Han BAI Zhaoguang LU Chunling DI Guodong

(DFH Satellite Co., Ltd.，Beijing 100094，China)

On-orbit lunar calibration takes advantage of not relying on calibration field or weather and is more effective. But attitude control and imaging parameters matching design problem should be solved. An attitude maneuver compensation method is proposed for the optical remote sensing satellite to solve the mismatch of integral time and scanning rate when the TDICCD camera carries out the lunar imaging task. And a sun-synchronous orbit remote sensing satellite is taken as an example for analysis. The satellite’s compensation angular velocity which enables the regular imaging is calculated and verified by the simulation software. The simulation method shows that the method proposed in this article can be used to match integral time and scanning rate and obtain valid lunar images.

TDICCD；lunar imaging；attitude maneuver compensation

2015-11-17；

2016-03-27

高涵，男，碩士研究生，研究方向為航天器總體設計。Email：m18600208173@163.com。

V412.4

A

10.3969/j.issn.1673-8748.2016.04.002