基于壓縮感知的脈搏信號重構方法研究
【作 者】張愛華,歐繼青,丑永新,楊彬
1 蘭州理工大學電氣工程與信息工程學院, 蘭州市,730050
2 甘肅省工業過程先進控制重點實驗室, 蘭州市,730050
基于壓縮感知的脈搏信號重構方法研究
【作 者】張愛華1,2,歐繼青1,2,丑永新1,2,楊彬1
1 蘭州理工大學電氣工程與信息工程學院, 蘭州市,730050
2 甘肅省工業過程先進控制重點實驗室, 蘭州市,730050
為了提高動態脈搏信號檢測過程中信號存儲和傳輸的效率,減少信號中的冗余,該文結合脈搏信號的稀疏性,提出一種改進的自適應匹配追蹤算法。該算法在稀疏自適應匹配追蹤算法的基礎上,采用變步長和雙閾值判別條件用于提高估計信號稀疏度的準確性。將所提出的算法用于建模的脈搏信號和實際采集的脈搏信號,結果表明:該算法能夠快速、準確地估計信號稀疏度,具有良好的抗噪性。與現有的稀疏自適應匹配追蹤算法和正交匹配追蹤算法相比,該算法重構速度快、精度高。
壓縮感知;匹配追蹤;SAMP;脈搏信號
0 引言
隨著嵌入式技術、傳感器技術和無線通信技術的發展,各種小型的、便攜的醫療設備廣泛用于人體健康監護和疾病診斷。但對于一些便攜式監護儀和無線遠程醫療監護系統而言,由于存儲空間和電池容量有限,若采用傳統的信號采集方法,不僅會占用系統大量的存儲空間,而且在數據存儲和傳輸過程中會占用系統大量的處理時間,增加系統的功耗。與傳統的采集方法相比,壓縮感知技術同時進行數據采集和壓縮[1-2],既節約了存儲空間,也降低了功耗。由于壓縮感知具有如此優點,已有學者將其應用于人體無線遠程醫療監護系統[3-4]。趙曙光等[5]分析了DCT變換基下脈搏信號的稀疏特性,并且利用OMP和E-OMP算法對壓縮后的脈搏信號重構。文獻[6] 中采用Gabor變換進行稀疏化處理,并使用JOMP算法實現了多傳感器脈搏信號重構。但是這些算法需要信號稀疏度信息,且對含噪的信號重構精度不高。因此,有學者提出了稀疏自適應匹配追蹤算法(Sparse Adaptive Matching Pursuit, SAMP)[7]以及在其基礎上的改進算法[8-9],可用于未知稀疏度信號的重構。但這些算法只用單一迭代停止條件,不能準確估計信號稀疏度,導致對較低信噪比信號重構精度不高。
針對上述這些算法的不足,本文利用脈搏信號的稀疏特性,提出了一種改進的自適應匹配追蹤算法(Modified Adaptive Matching Pursuit,MAMP)。該算法在重構過程中使用變步長的方法[9]和雙閾值判別條件—余量能量和余量能量變化率[10],快速、準確地恢復了原始脈搏信號。本文選用建模的信號驗證所提方法的準確性和抗噪性并將此方法用于實際采集的脈搏信號。
1 方法
1.1 壓縮感知原理
壓縮感知的前提條件為信號是稀疏的或可壓縮的,即信號中只含有少量的非零元素。然而,在時域內大多數信號不是稀疏的,但在一些變換域中是稀疏的或近似稀疏的,如Fourier變換、小波變換、DCT變換、Gabor變換等。對于長度為N的離散信號x,在某個正交基φi為N維列向量)下線性表示為:
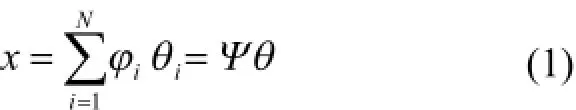
式中Ψ為正交基,θ為稀疏信號。若θ中有K(K<<N)個數不為零,則稱x是K稀疏信號。
測量矩陣是實現信號壓縮的關鍵,在信號采集階段通過M×N維的測量矩陣φ,可將N維信號x壓縮為M(M<<N)維的y信號,如下式所示:
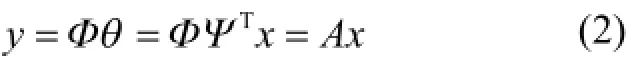
為了保證測量信號能被精確地重構出來,測量矩陣φ必須滿足約束等距性質(RIP)[11]。但實際中判斷一個矩陣是否滿足RIP性質很難,故常用其等價形式[12],判斷測量矩陣φ和稀疏變換基Ψ間的相關性,如下式所示:
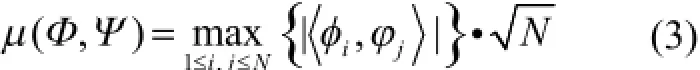
式中相關系數μ(φ, Ψ)越小,則φ和Ψ間非相關性越大,重構后信號質量越高。
信號重構就是從測量信號y中恢復原始信號x,即求解線性方程組y=φθ,再通過反變換求出x。表面上看,由于未知數大于方程數,此方程無法求解。但是,由于θ是稀疏的,則可以通過最優l0范數的方法求解此方程,如下式所示:
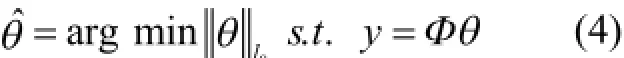
式中,‖●‖l0表示向量θ中非零元素的個數。
1.2 改進的自適應匹配追蹤算法
目前,大多數重構算法,如MP、OMP、BP算法等,需要信號稀疏度先驗信息, SAMP算法對其進行了改進,采用余量能量作為迭代停止條件,實現了未知稀疏度信號重構。但也存在一些缺陷[8-9]:(1) 預選階段原子過多,會造成預選原子錯誤且在候選階段消耗大量的時間;(2) 固定步長不能準確地估計信號稀疏度;(3) 僅用單一迭代停止條件,不能準確估計信號稀疏度且在較低信噪比時,重構精度不高。
針對這些不足,本文提出了MAMP算法。在初選階段,采用固定的閾值方案取代原來的選擇方案(Sk=max(u, length))。每次只將u中最大的m個元素放入索引集Sk=max(u, m)。其中m為常數,u為余量與測量矩陣的內積。這樣可避免因預選原子過多而造成的預選錯誤和后選集的時間消耗。為了能夠準確地估計信號稀疏度,對SAMP算法的迭代停止條件和步長選擇方法進行了改進,采用余量能量和余量能量變化率作為迭代停止條件;使用變步長的方法,當余量能量小于設定閾值時,步長置為1。MAMP算法基本步驟如下:
輸入:測量信號y,測量矩陣φ,閾值ε1、ε2、ε3,步長l;
步驟1 初始化
余量r=y,支撐集長度length=l,m=30,階段stage=1,迭代次數k=1,索引集S=?,候選集C=?,支撐集F=?,θ=0;
步驟2 循環迭代
2) 計算索引集:將u中最大的前m個元素的下標加入索引集Sk=max(u, m);
4) 若 Ck的長度小于length不裁剪,Fnew=Ck,否則執行下一步進行裁剪;
5) 計算Ck中索引值對應原子與余量rk-1的相關系數,并取相關系數最大的length個原子存入Fnew;
驟2;
5) 更新支撐集Fk=Fnew,rk=rnew,k=k+1,轉步驟2;
步驟4 輸出計算
其中,符號“?”表示偽逆,“‖●‖2”表示2范數,rk為第k次迭代時的余量,Fk為第k次迭代時稀疏信號的支撐集,為觀測矩陣子矩陣,由支撐集中下標所對應的列向量組成,θ為重構后的稀疏信號,x為重構后的信號。
2 實驗數據
實際采集的脈搏信號受到噪聲的干擾,無法獲得脈搏信號的真值,實驗中選用建模的脈搏信號驗證方法的準確性和抗噪性。建模的脈搏信號由三個高斯函數合成,分別對應實際脈搏信號的主波、重搏前波和重搏波。每個高斯函數由幅值V、時間T和寬度U這3個參數確定[13],如下式所示:
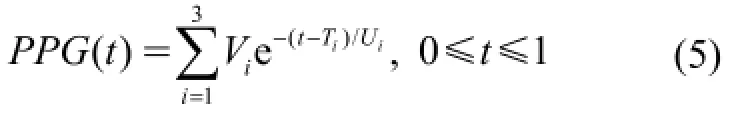
式中,V1=0.8, T1=0.25,U1=0.012,V2=0.5,T2=0.45,U2=0.01,V3=0.4,T3=0.7, U3=0.03。將(5)式產生的脈搏信號進行延拓,得到干凈的脈搏信號x(t);若數據點間隔為1/250,則采樣頻率fs為250 Hz。為了消除信號幅值不同造成的影響,對其進行歸一化(均值為0,方差為1)處理,具體如下式所示[14]:
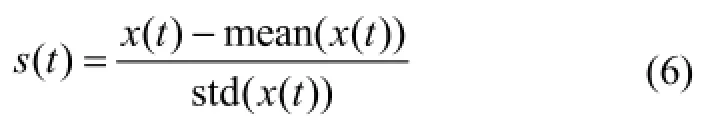
式中,mean(x(t))、std(x(t))分別為脈搏信號x(t)的均值和標準差,s(t)為歸一化處理后的脈搏信號,如圖1(a)所示。

圖1 噪聲污染前后的脈搏信號Fig.1 The PPG signals before and after noise pollution
此外,選用美國麻省理工學院PhysioNet/MIMIC數據庫和課題組實際采集的脈搏信號。其中,MIMIC數據庫收集了重癥監護者的多種生理信號,包括脈搏信號、心電信號和血壓信號等等,采樣頻率為125 Hz,采樣時間為1 h;課題組脈搏信號由便攜式多生理信號采集系統獲得,采集對象為20~25歲的健康大學生,采樣頻率為1 kHz,時間為10 min。
選用PhysioNet/MIT-BIH / Noise Stress Test數據庫的噪聲信號[14],并加入建模的脈搏信號中,驗證所提出方法的抗干擾性。噪聲信號主要包括基線漂移和肌電干擾(含有工頻干擾),采樣頻率為360 Hz,時間為1 h。
3 實驗結果
3.1 方法的準確性分析
為了驗證所提方法的準確性,選取建模的脈搏信號。首先采用DCT變換進行稀疏化處理,然后利用隨機高斯矩陣進行數據壓縮,最后采用所提出的MAMP方法進行信號重構。由于實驗數據長度太長、所需要的觀測數M過大,實驗中采用滑窗的方法,每次以fs個數據點為窗口長度進行重構。實驗中其他參數設置:閾值ε1,ε2,ε3分別為0.001、1×10-5、0.01;步長l為6;OMP算法的迭代次數k設置為35;窗口長度N=fs;觀測數M=80。使用均方根誤差(Mean Square Error, MSE)[14]評估所提出方法重構后信號的質量,如下式所示:
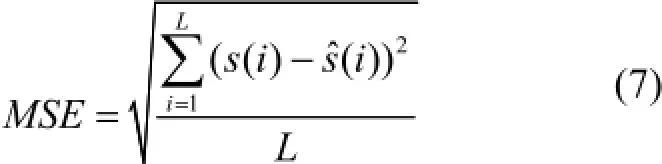
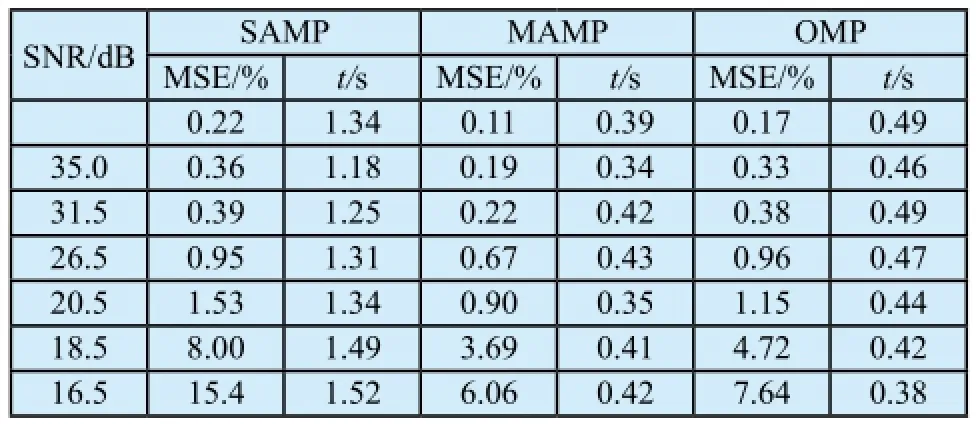
表1 不同信噪比下重構信號的MSE和tTab.1 The MSE and t of signals under various SNRs
3.2 方法的抗噪性分析
由于無法準確獲得實際脈搏信號的信噪比(Signal Noise Ratio,SNR),實驗中采用Noise Stress Test數據庫提供的噪聲與建模的脈搏信號s(t)疊加,產生的信號來驗證MAMP算法的抗噪性[14]。噪聲選用數據庫中的基線漂移和肌電干擾信號,給其乘以不同的噪聲系數[14]可以得到不同信噪比的脈搏信號,如表2所示。假設n(t)為噪聲信號,則n(t)=a1·bw(t)+a2·ma(t);式中bw(t)為基線漂移,ma(t)為肌電干擾,a1、a2為噪聲系數。為了消除脈搏信號和噪聲采樣頻率不統一造成的影響,需要對噪聲信號n(t)進行均勻降采樣。然后截取長度相同的噪聲信號n(t)加入s(t)得到含噪聲的脈搏信號,通過下式計算信號的信噪比[14]:
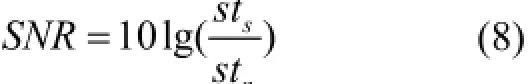
式中,sts為信號s(t)的方差,stn為信號n(t)的方差。
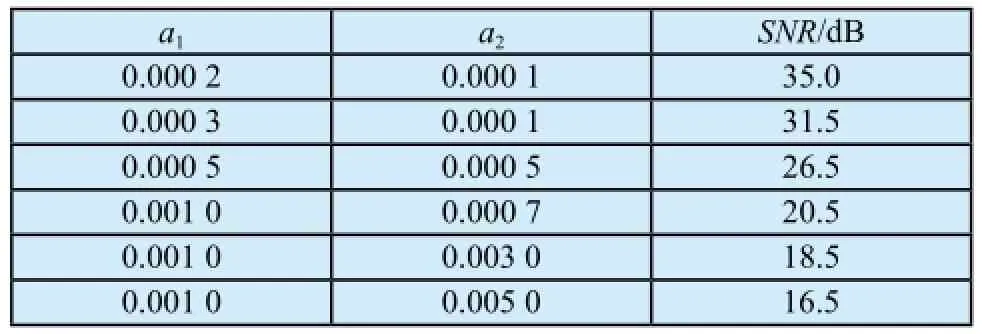
表2 噪聲系數和信噪比關系Tab.2 The relationship of noise scale and SNR
表1中2至7行是不同噪聲情況下重構信號的MSE和重構時間。從表1中可以看出隨著信噪比的減小,各方法重構后信號的MSE值不斷增大。其中,當信噪比大于26.5 dB時,MAMP、SAMP和OMP方法的MSE值不超過1.0%,受噪聲影響較小;當信噪比小于26.5 dB時, 三種方法受噪聲影響變化較大;16.5 dB(圖1(b))時SAMP方法已超過10%,MAMP和OMP方法小于8%。采用式(8)計算不同信噪比下重構后信號的信噪比,如圖2所示。
從圖2中可以看出,隨著信噪比的增大,各方法重構后信號的信噪比均增加且高于輸入信號的信噪比,這是因為消除了部分干擾信號。由壓縮感知原理可知,很難消除低頻信號的影響,可以降低高頻噪聲的影響。在信噪比較低時,MAMP方法較其他兩種方法明顯提高了2~5 dB,因此驗證了MAMP方法在較低信噪比能更準確估計信號稀疏度,抗噪性強。

圖2 重構性能與信噪比關系Fig.2 The relationship of reconstructed performance and SNR
3.3 采樣頻率對方法的影響
為了分析采樣頻率對重構信號質量的影響,采用所提出的MAMP方法重構不同采樣頻率下的脈搏信號,結果如表3所示。SAMP方法的MSE值約為0.30%,時間在1.3 s左右;OMP方法的MSE值為0.1%~0.3%,時間為0.4~1.5 s;MAMP方法的MSE值為0.12%左右,時間約為0.35 s。從表3中可以看出,本文所提出的方法幾乎不受采樣頻率的影響,其他兩種方法重構的信號受到采樣頻率的影響較大。
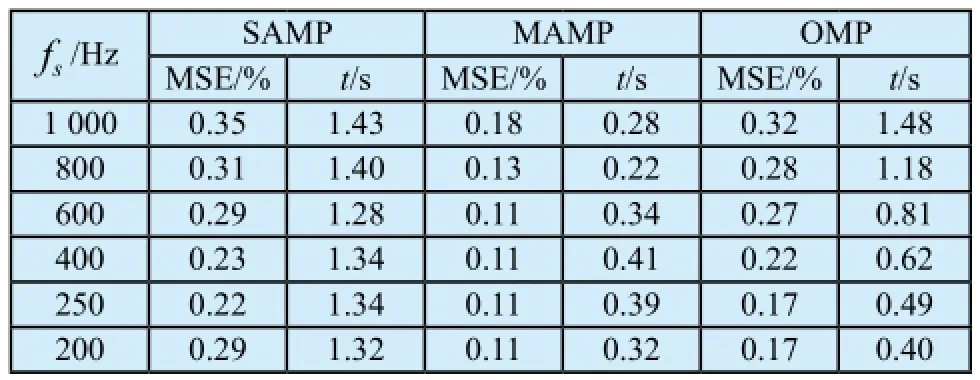
表3 不同采樣頻率下重構信號的MSE和tTab.3 The MSE and t under various sampling frequency
3.4 方法的應用
實驗中選取PhysioNet/MIMIC數據庫中20組病人數據(數據名稱:208m~230m)和課題組采集的20名健康者的脈搏信號進行實驗,結果分別如圖3和圖4所示。從圖中可以看出,重構前后的脈搏信號非常相似,各拐點位置無明顯變化,本文提出的方法能夠用于脈搏信號的重構。
4 結論
針對現有的重構算法只用單一迭代停止條件,不能準確估計信號稀疏度和重構精度不高等問題,本文提出了MAMP方法。此方法能夠自適應于信號的稀疏度,快速準確地恢復脈搏信號。實驗結果表明,MAMP算法受信號采樣頻率影響小,重構速度快,能夠準確地重構出脈搏信號,且在較低信噪比時重構精度高。

圖3 MIMIC數據庫脈搏信號重構結果Fig.3 The reconstructed results of MIMC database signal

圖4 課題組采集的脈搏信號重構結果Fig.4 The reconstructed results of acquisition signal
[1] Jin J, Gu YT, Mei SL. A stochastic gradient approach on compressive sensing signal reconstruction based on adaptive filtering framework [J]. IEEE J Select Topics Sign Proc, 2010, 4(2): 409-420.
[2] 余凱, 李元實, 王智, 等. 基于壓縮感知的新型聲信號采集方法[J].儀器儀表學報, 2012, 33(1): 105-112.
[3] Craven D, McGinley B, Kilmartin L, et al. Compressed sensing for bioelectric signals: a review[J]. IEEE J Biomed Health Inform,2015, 19(2): 529-540.
[4] Zhang Z, Jung TP, Makeig S, et al. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware[J]. IEEE Trans Biomed Eng, 2013, 60(1): 221-224.
[5] 康如婷, 趙曙光, 劉浩. 一種高效的PPG壓縮感知重構算法[J]. 計算機工程與應用, 2014, 50(14): 131-134.
[6] Hu FY, Li SS, Xue T, et al. Design and analysis of low-power body area networks based on biomedical signals[J]. Int J Electron, 2012, 99(6): 811-822.
[7] Do TT, Lu G, Nguyen N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Conf Sign Syst Comput, 2008, 581-587.
[8] 甘偉, 許錄平, 羅楠, 等. 一種自適應壓縮感知重構算法[J]. 系統工程與電子技術, 2011, 33(9): 1948-1953.
[9] 朱延萬, 趙擁軍, 孫兵. 一種改進的稀疏度自適應匹配追蹤算法[J]. 信號處理, 2012, 28(1): 80-86.
[10] 呂方旭, 張金成, 王泉, 等. 基于傅里葉基的自適應壓縮感知重構算法[J]. 北京航空航天大學學報, 2014, 30(4): 544-550.
[11] Candes E. The restricted isometry property and its implications for compressed sensing[J]. Comput Rendus Math, 2008, 346(9/10): 589-592.
[12] Baraniuk R, Davenport M, Devore R, et al. A simple proof of the restricted isometry property for random matrices[J]. Construct Approximat, 2008, 28(3): 253-263.
[13] 張愛華, 胡文龍, 丑永新. 基于循環平穩算法的脈搏信號質量評估與濾波[J]. 中國醫療器械雜志, 2015, 39(2): 83-86.
[14] 丑永新, 張愛華, 楊曉華. 基于改進滑窗迭代DFT的動態脈率變異性提取[J]. 儀器儀表學報, 2015, 36(4): 812-821.
Research on PPG Signal Reconstruction Based on Compressed Sensing
【 Writers 】ZHANG Aihua1,2, OU Jiqing1,2, Chou Yongxin1,2, YANG Bin1
1 College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou, 730050,
2 Key Laboratory of Gansu Advanced Control for Industrial Processes, Lanzhou, 730050
compressed sensing, matching pursuit, sparse adaptive matching pursuit, photoplethysmography signal
R318.6;TN911.7
A
10.3969/j.issn.1671-7104.2016.01.002
1671-7104(2016)01-0005-05
2015-09-14
國家自然科學基金資助項目(81360299);甘肅省自然科學基金資助項目(145RJZA065);模式識別國家重點實驗室開放課題(201407347)。
張愛華,教授,博士生導師,E-mail: lutzhangah@163.com
【 Abstract 】In order to improve the storage and transmission efficiency of dynamic photoplethysmography (PPG) signals in the detection process and reduce the redundancy of signals, the modified adaptive matching pursuit (MAMP) algorithm was proposed according to the sparsity of the PPG signal. The proposed algorithm which is based on reconstruction method of sparse adaptive matching pursuit(SAMP), could improve the accuracy of the sparsity estimation of signals by using both variable step size and the double threshold conditions. After experiments on the simulated and the actual PPG signals, the results show that the modified algorithm could estimate the sparsity of signals accurately and quickly, and had good anti-noise performance. Contrasting with SAMP and orthogonal matching pursuit(OMP), the reconstruction speed of the algorithm was faster and the accuracy was high.

