一類擬線性橢圓型方程div(|Du|p-2Du)=f(x,u,Du)的有界正整解1

許興業

（廣東外語外貿大學南國商學院公共課教學部；廣東廣州 510545）

一類擬線性橢圓型方程div(|Du|p-2Du)=f(x,u,Du)的有界正整解1

許興業

（廣東外語外貿大學南國商學院公共課教學部；廣東廣州 510545）

以Schauder-Tychonoff不動點定理為工具；研究一類形如div(|Du|p-2Du)=f(x,u,Du)的擬線性橢圓型方程正的有界整體問題；得到了2個有界正整解的存在性定理.

擬線性橢圓型方程；有界正整解；Lebesgue控制收斂定理；閉凸子集；連續映照；不動點定理

1 引言與預備定理

有關非線性橢圓型方程正整解存在性的研究；較多的文章是研究方程左邊為形如Δu,Δ2u及Δmu的調和；雙調和及多重調和方程［1-5］.但對形如下面的擬線性橢圓型方程

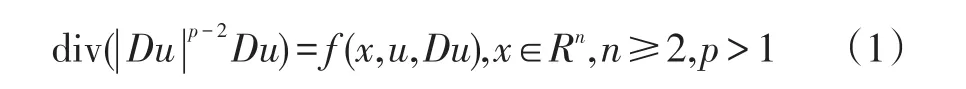
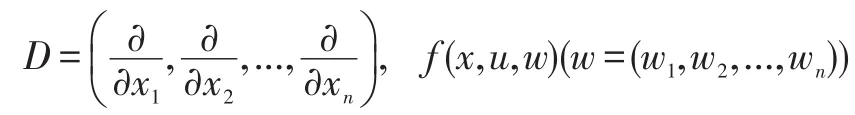
下面給出上、下解的定義及預備定理.

預備定理設f滿足條件：

（a）f(x,u,,w)在Rn×R+×Rn上連續；且局部Holder連續（指數θ∈(0,1)）；（b）對任一有界區域Ω?Rn,存在ρ(Ω,M)＞ 0；使

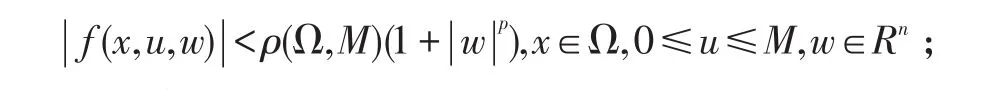
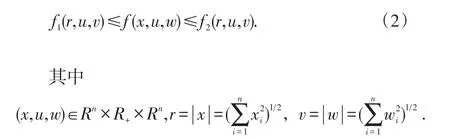
預備定理的證明參見文獻［1］.

2 主要結果

在下面的討論中引入記號；不再贅述：

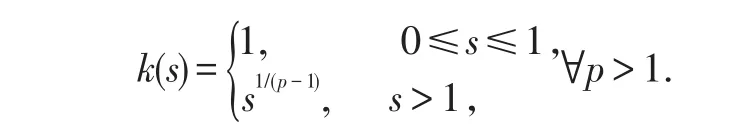
定理1設f滿足預備定理中的（a）、（b）、（c）和下列條件：

（i）f1(r,u,v)與f2(r,u,v)關于u,v∈R+都是非減函數；

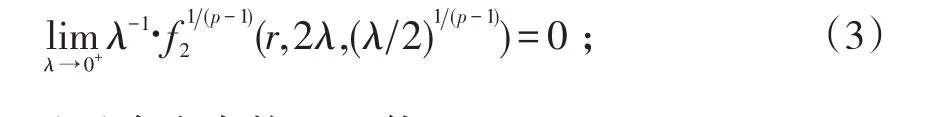
（iii）存在常數c＞0使

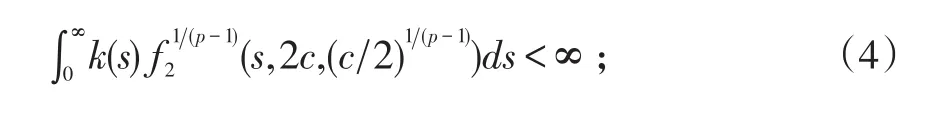
則方程（1）存在無窮多個有界正整解u(x).

證明由（2）式可知方程

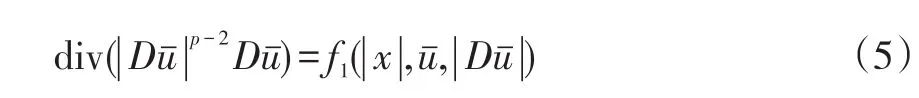
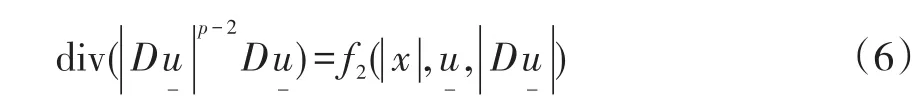
下面討論積分方程（8）的可解性.由（ii）知

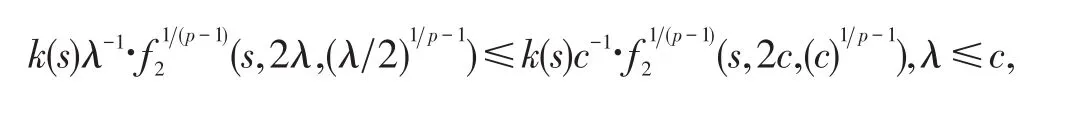
其中c是（iii）中出現的常數；且對每一s∈(0,∞),當λ→0+時有

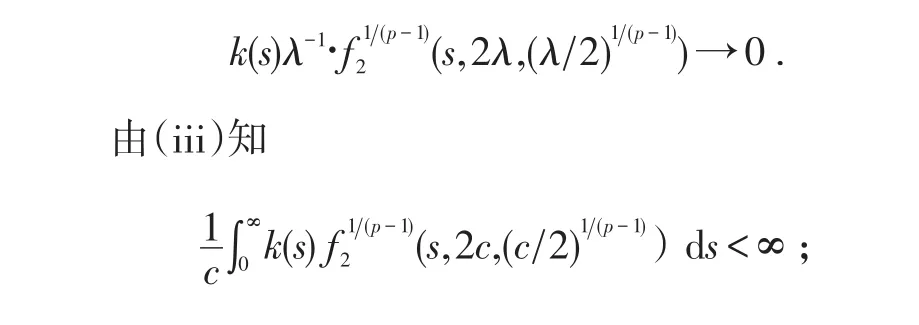
于是由Lebesgue控制收斂定理得

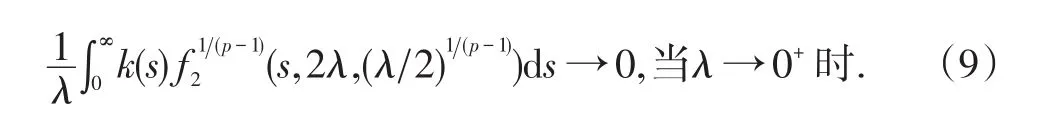
進而由（2）推出：對?p＞1有

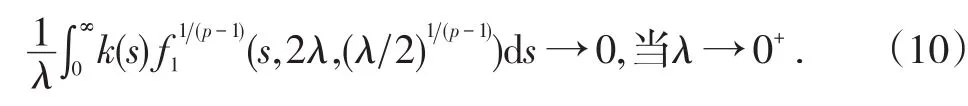
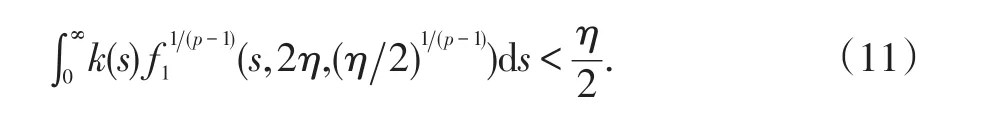
由（10）知可以選擇充分小的常數η＞0使得記C1[0,∞)是定義在[0,∞)上的所有連續可微函數作成的空間；依通常的方法引入C1[0,∞)的拓撲.作集合：

在這里補充定義：

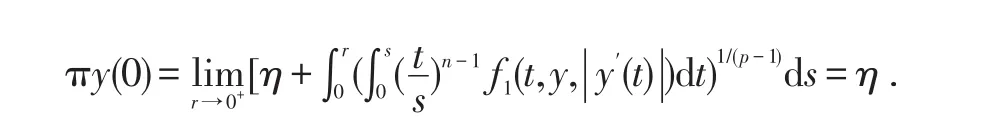
下面證明映射π滿足：

（II）π是連續映射.

設yi∈Σ(i=1,2,...)且依C1[0,∞)的拓撲yi收斂于y；對?r∈[0,∞)由（12）、（14）式得

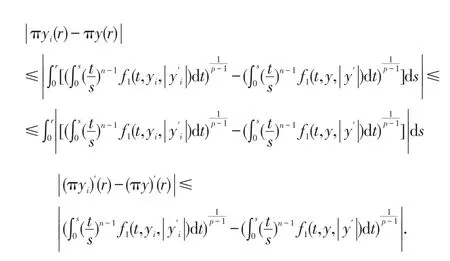
（III）πΣ是相對緊的.

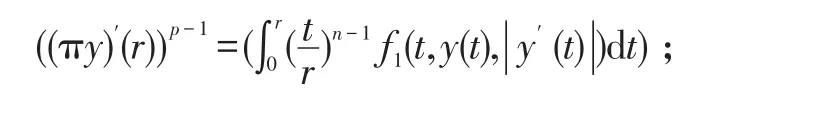
又注意到（12）式中的r≥ 0；及f(r,u,v)≥0

對（17）式右邊的積分我們約定

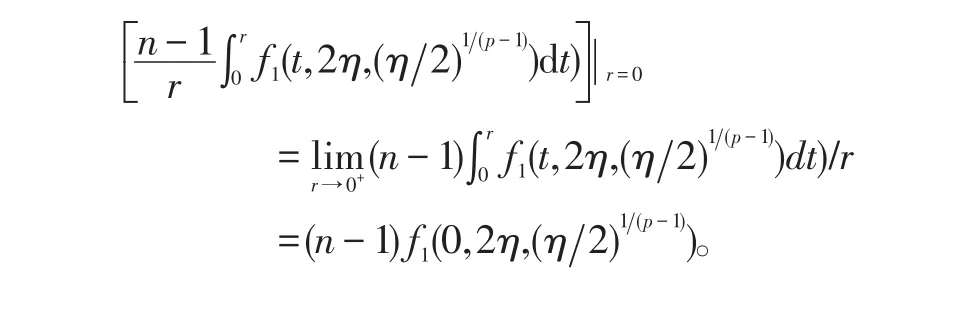
于是（17）式對任意r≥0成立.故有