異地雙活數據中心服務區域劃分優化

丁建立　王斌強　張　超

1(中國民航大學中國民航信息技術科研基地　天津 300300)

2(中國民航大學計算機科學與技術學院　天津 300300)

?

異地雙活數據中心服務區域劃分優化

丁建立1,2王斌強2張超2

1(中國民航大學中國民航信息技術科研基地天津 300300)

2(中國民航大學計算機科學與技術學院天津 300300)

摘要異地雙活數據中心是現在傳統大型數據中心的發展趨勢。針對國內某民航旅客服務信息系統高并發在線交易、大規模海量數據處理、應急響應和災難快速恢復等要求，提出一種基于球面Voronoi圖的異地雙活數據中心服務區域劃分方法。該方法考慮了數據中心最大負載量的受限性和所有被分配用戶訪問到各自數據中心的總距離最小化，并在求解過程進行了雙曲化優化逼近和用戶分布估計。實驗結果表明，在不同訪問用戶條件下，該方法都能重新調整用戶訪問數據中心的接入點，給出合理的區域劃分。該方法能均衡單數據中心的系統訪問壓力，為大數據時代數據中心建設和災備系統建設提供技術支持。

關鍵詞球面Voronoi圖異地雙活數據中心民航最大負載服務區域劃分

OPTIMISING DIVISION OF SERVICE REGIONS OF DISTANT DOUBLE LIVE DATA CENTRE

Ding Jianli1,2Wang Binqiang2Zhang Chao21

(Information Technology Research Base,Civil Aviation Administration of China,Tianjin 300300,China)2(College of Computer Science and Technology,Civil Aviation University of China,Tianjin 300300,China)

AbstractDistant double live data centre is nowadays the development trend of traditional large data centres. According to the requirements of a certain China’s civil aviation passengers information service system, which includes highly concurrent online transactions, large-scale mass data processing, emergency response and quick disaster recovery, the paper presents a service region divistion solution for distant double live data centre, which is based on Voronoi diagram on the sphere. This solution takes into consideration the property of data centre’s peak load being constrained and the minimising of total distance that all the assigned users accessing to the data centre of each own, and makes hyperbolic optimised approximation and users’ distribution estimation in calculation process. Experimental results show that whatever the users’ access is, this scheme can all readjust the access points of users when accessing the data centre, and offers reasonable region division. The scheme can balance the system access pressure of single data centre, and provides technical support for the construction of data centre and disaster recovery system in big data era.

KeywordsVoronoi diagram on the sphereDistant double liveData centreCivil aviationPeak loadDivision of servant regions

0引言

隨著民航業的迅速發展，現有的民航旅客服務信息系統在存儲海量數據、進行大規模數據分析處理、大并發在線交易快速響應、容災備份、應急恢復等能力方面都逐漸顯現出了不足。因此，為了適應民航業的發展需求，國內某民航旅客服務信息提供商計劃建立異地雙活數據中心，以平衡系統訪問壓力、改善用戶體驗，實現民航信息系統的高可靠性和高可用性。

存在多個生產數據中心時，一般是每個數據中心根據用戶自適應接入機制，只為各自固定的區域用戶提供服務，通常是依靠全局負載均衡[1](GSLB)裝置。用戶在訪問多個數據中心時，GSLB根據DNS探測用戶位置，將用戶請求接入距離用戶最近的數據中心并返回結果，這種方式減少了網絡訪問延遲，改善了用戶體驗。但這種方式沒有考慮到每個數據中心的最大負載量，當訪問急劇攀升超過原來數據中心的最大閾值時，為減輕數據中心的負載壓力，就應該將原來區域的部分用戶請求合理轉移到其他數據中心。由于地球本身近似球形，而球面Voronoi圖在全球數據的管理和球面空間關系的動態維護具有優秀的性質[2]。所以，本文在基于球面Voronoi圖劃分的基礎上，結合各數據中心的最大負載量限制和用戶距離的最小化，給出了一種重新調整原有劃分的方法，以確定不同用戶訪問量下的服務區域。

1球面Voronoi圖的概念

Voronoi圖是分割空間的一種方法，和Delaunay多邊形呈對偶關系，Voronoi圖利用最近鄰近原則將空間劃分為多個區域，使得每個區域內的點距離其所在空間的生長點最近[3]。最早由俄國數學家M.G.Voronoi于1908年提出，并將其擴展至高維空間。本文將Voronoi圖擴展到球面進行應用。球面Voronoi圖[4]的數學定義:

球面R2為非歐式空間，設P={P1,P2,…,Pn}(2≤n≤∞)為球面R2上的對象點集，Xi和Xj分別為點Pi∈R2和Pj∈R2的位置矢量，點Pi和Pj之間的最短距離定義為通過兩點的大圓中較小弧段的長。用公式表示為：

(1)

稱此距離為Pi和Pj之間的球面距離，稱：

V(Pi)={P|d(P,Pi)≤d(P,Pj),j≠i,P∈R2}

i=1,2,…,n

(2)

為關于Pi的球面的Voronoi多邊形，稱球面Voronoi多邊形的集合為球面R2上點P的球面Voronoi圖，P1,P2,…,Pn為生成點，如圖1、圖2所示。

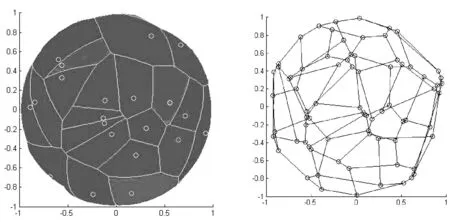
圖1　半徑為1的球面Voronoi圖　　圖2　對應的Delaunay三角網

2異地雙活數據中心服務區域劃分優化

2.1異地雙活的概念

異地雙活[5]數據中心是現在傳統大型數據中心的發展趨勢。“異地”相對于同城而言，一般不在同一城域；“雙活”區別于一個數據中心、一個災備中心的模式，前者兩個數據中心都處于運行當中，所以稱為“雙活”，且互為備份；后者是一個數據中心投入運行，另外一個數據中心處在不工作狀態，只有當災難發生時，生產數據中心癱瘓，災備中心才啟動。圖3是國內某民航旅客服務信息提供商異地雙活數據中心架構示意圖。

圖3　國內某民航旅客服務信息提供商異地雙活數據中心架構示意

2.2基于球面Voronoi圖的異地雙活模型

為了科學合理的將多余的用戶分配到新的數據中心，本文做了如下假設。第一，所有數據中心的位置都已確定，數據中心的最大負載量用能為多少用戶量提供服務表示，總容量能容納所有的用戶，并且所有用戶的請求都是平等的；第二，研究的空間區域是全國范圍，區域內的訪問用戶分布和區域的人口分布成正比。

本文主要基于國內某民航旅客服務信息提供商的異地雙活數據中心進行研究，僅生成兩點的球面Voronoi圖，將生成點P構成的集合P={P1,P2}當成數據中心，形成的區域記為ε1和ε2，U={U1,U2,…,UN}是當前存在的N個用戶，由于各區域內的用戶到各自生成點P的距離都是最短的，所以將ε1區域內的用戶訪問分配給P1，ε2區域內的用戶訪問分配給P2，各用戶到其所分配的數據中心之間的總距離記為：

(3)

其中j=j(i)是第i個用戶分配到第j(i)個數據中心的分配函數，d(Pj(i),Ui)表示球面上點Pj(i)和Ui之間的最短距離，可由式(1)得到。設Ci是數據中心Pi的最大負載量，最大負載量控制定義:Ni≤Ci，式中，Ni是分配到數據中心Pi的實際人數。

當沒有最大負載量限制時，這種劃分能很好地滿足訪問距離的最小化，但現實并非如此，由于原先數據中心設施設計不足或者短期內用戶訪問劇增，就需要采取措施對訪問進行轉移。如N1>C1時，必須將ε1區域內的部分用戶從數據中心P1轉移到數據中心P2，使得N1≤C1，此時距離將產生增量：

(4)

其中u12表示從數據中心P1轉移到數據中心P2的用戶的集合。

為了達到轉移后距離最優，只需要找到一種使ΔD(j)最小的方法即可。

2.3雙曲化優化逼近

在求解ΔD(j)最小化問題時，我們可以應用雙曲線的性質進行求解。雙曲線在Voronoi圖上的性質和應用有很多的研究[6-8]，文獻[9]指出，在有約束限制的最小化分配問題，可以通過雙曲線的調整獲得。所以本文在球面上基于點P1和P2構造雙曲線，雙曲線如下表示：

d(X,P2)-d(X,P1)=2k

(5)

通過調整k值進行區域逼近，直到N1≤C1。

區域調整，導致P1數據中心區域內的用戶數N1發生改變，所以程序中通過函數Get Curr User Nums()獲得當前的用戶數，具體是統計當前區域內的城市數，計算其人口總和，以一定比例的人口數作為當前區域內的訪問用戶數。

為防止過多用戶從數據中心P1轉移到P2，降低數據中心的利用率。本文假定，最終劃分后，數據中心的負載量與最終分配到該中心的用戶數量的差應小于1000，逐步逼近生成雙曲線的偽代碼表示如下，其中Xi是弧P1P2間上的點，借鑒取半查找的思想，通過ki×(1/2)×d(P1,P2)確定Xi的位置，進而應用式(5)生成當前ki條件下對應的雙曲線。

begin

1?i

N1=GetCurrUserNums()

while N1>C1or(C1-N1)>1000

{

d(Xi,P1)=ki×(1/2)×d(P1,P2)

//GetCurrUserNums()函數獲取當前區域內的用戶數

N1=GetCurrUserNums()

if N1>C1

{

i+1?i

}

else

{

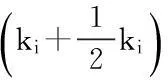
i+1?i

}

}

returnki

end

2.4用戶分布估計

在每一次進行雙曲劃分后，都需要重新計算該區域內的用戶數量，為使實驗方便，選擇了分布在全國的如北京、上海等77個百萬級人口城市[10]，訪問用戶數將以一定比例從城市人口總數中提取。本文生成了包含人口、經度和緯度的城市kml文件，其中所有城市地理信息都包含在字段內，字段通過包含、、等子字段來表示單個城市具體信息，如字段中population屬性表示城市人口數，字段表示城市名稱，字段表示當前城市的經緯度。kml文件格式示例如下：

xmlns:gx=″http://www.google.com/kml/ext/2.2″

xmlns:kml=″http://opengis.net/kml/2.2″

xmlns:atom=″http://www.w3.com.org/2005/Atom″>

population: 20217700

division: Shanghai

reference:

……

3模擬計算與結果分析

圖4　未考慮負載時的初始劃分

基于國內某民航旅客服務信息提供商的北方(116.46，39.92)和南方(120.76，30.77)兩個數據中心，本節編寫代碼生成球面Voronoi圖，并通過調用google maps API 生成可視化仿真演示系統。圖4顯示的就是在沒有最大負載約束條件下基于球面Voronoi圖的服務區域劃分，粗弧線以上的區域都分配給北方數據中心，粗弧線以下的區域分配給南方數據中心。

在確定數據中心最大負載時，分析了全球其他三大民航旅客服務信息提供商數據中心的規模，針對提供商數據中心的每秒處理能力，以系統可承受一分鐘持續訪問處理量作為數據中心的可承受最大負載量，如表1所示。

表1　各提供商最大負載量

圖5　以國外A系統最大負載量作為用戶

由于南方數據中心規模很大，所以實驗時我們只考慮北方數據中心的最大負載，并分別將其他三大GDS的最大負載量作為用戶訪問的最小量，對北方數據中心的服務區域分別進行劃分。圖5中細弧線是當有1 350 000用戶訪問，對北方數據中心所優化的服務區域，調整后，區域內用戶的訪問不超過數據中心的最大負載900 000，圖6、圖7分別表示當2 220 000和2 520 000用戶訪問時的劃分。可以看出，隨著訪問量的增加，細弧線相應向北移動，使得北方數據中心的服務區域相應減少。

4結語

異地雙活數據中心作為當前最先進的建設模式，國內外相關的研究還比較少，同時雖然對于Voronoi圖，國內在地理[11]、氣象等領域有較多的研究，但將其引入到異地雙活數據中心的研究還沒有。所以本文通過對球面Voronoi圖的研究，結合國內某民航旅客服務信息系統數據中心的實際建設及應用背景，提出了一種服務區域優化的方法，考慮了數據中心最大負載的限

制和總距離的最優化，對不同用戶訪問量進行了仿真，能科學合理地均衡數據中心的大規模訪問量。整體實驗結果比較合理，有一定的實用價值。

參考文獻

[1] 呂海燕,車曉偉,張杰.基于“偽HTTP Server”的CDN本地負載均衡實現方式[J].計算機技術與發展,2013,23(6):46-49.

[2] 趙學勝,陳軍,王金莊.基于O-QTM的球面Voronoi圖的生成算法[J].測繪學報,2002,31(2):157-163.

[3] 龔詠喜,劉瑜,鄔倫,等.基于帶權Voronoi圖與地標的空間位置描述[J].地理與地理信息科學,2010,26(4):21-26.

[4] 張麗平,李松,郝忠孝.球面上的最近鄰查詢方法研究[J].計算機工程與應用,2011,47(5):126-129.

[5] TechTarget數據中心[OL].(2013-1-25).[2014-6-10].http://www.searchdatacenter.com.cn/shoontent_70148.htm.

[6] Nielsen F,Nock R.Hyperbolic Voronoi diagrams made easy[C]//Computational Science and Its Applications (ICCSA),2010 International Conference on.IEEE,2010:74-80.

[7] Bogdanov M,Devillers O,Teillaud M.Hyperbolic Delaunay complexes and Voronoi diagrams made practical[C]//Proceedings of the 29th annual symposium on Symposuim on computational geometry.ACM,2013:67-76.

[8] Barclay M,Galton A.Comparison of region approximation techniques based on Delaunay triangulations and Voronoi diagrams[J].Computers Environment and Urban Systems,2008,32(4):261-267.

[9] Shanmugam S,Shouraboura C.Finding Optimal Allocation of Constrained Cloud Capacity Using Hyperbolic Voronoi Diagrams on the Sphere[J].Intelligent Information Management,2012,4(5):239-250.

[10] 維基百科.中華人民共和國特大城市列表[OL].(2014-4-7).

[11] 李久剛,唐新明,劉正軍,等.基于行程距離最優及容量受限的避難所分配算法研究[J].測繪學報,2011(4):489-494.

中圖分類號TP309

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.02.007

收稿日期：2014-07-11。國家科技支撐計劃項目(2012BAH21 F02)；2013年民航科技創新引導資金重大專項(MHRD20130106)；中國民航大學中央高校基金項目(3122014C016)；中國民航大學預研重大項目(3122014P004)。丁建立，教授，主研領域：民航信息系統，航空物流。王斌強，碩士生。張超，碩士生。