基于身份的認(rèn)證密鑰協(xié)商協(xié)議的改進(jìn)
陳 虹 徐嘉鴻 肖振久
1(遼寧工程技術(shù)大學(xué)軟件學(xué)院 遼寧 葫蘆島 125105)
2(中國(guó)傳媒大學(xué)計(jì)算機(jī)學(xué)院 北京 100024)
?
基于身份的認(rèn)證密鑰協(xié)商協(xié)議的改進(jìn)
陳虹1徐嘉鴻1肖振久2
1(遼寧工程技術(shù)大學(xué)軟件學(xué)院遼寧 葫蘆島 125105)
2(中國(guó)傳媒大學(xué)計(jì)算機(jī)學(xué)院北京 100024)
摘要針對(duì)已有的基于身份的認(rèn)證密鑰協(xié)商協(xié)議存在的安全問(wèn)題,提出一種改進(jìn)的基于身份的認(rèn)證密鑰協(xié)商協(xié)議。該協(xié)議采用雙線(xiàn)性對(duì)運(yùn)算方法, 用戶(hù)雙方的臨時(shí)和長(zhǎng)期私鑰結(jié)合進(jìn)行最終會(huì)話(huà)密鑰的計(jì)算,解決了原協(xié)議中存在的PKG前向安全性問(wèn)題、單一依賴(lài)臨時(shí)或長(zhǎng)期私鑰而存在的問(wèn)題和已知臨時(shí)會(huì)話(huà)密鑰泄漏攻擊的問(wèn)題。在保證改進(jìn)協(xié)議正確基礎(chǔ)上,對(duì)協(xié)議的安全屬性及協(xié)議性能進(jìn)行了分析。采用SVO邏輯對(duì)協(xié)議進(jìn)行形式化分析,驗(yàn)證了改進(jìn)協(xié)議的認(rèn)證性和安全性。結(jié)果表明,改進(jìn)的協(xié)議滿(mǎn)足基于身份認(rèn)證密鑰協(xié)商協(xié)議的所有安全性要求,與已有基于身份的認(rèn)證密鑰協(xié)商協(xié)議相比具有更好的安全屬性及計(jì)算效率。
關(guān)鍵詞基于身份的認(rèn)證密鑰協(xié)商雙線(xiàn)性對(duì)SVO邏輯形式化驗(yàn)證
IMPROVEMENT OF ID-BASED AUTHENTICATED KEY AGREEMENT PROTOCOL
Chen Hong1Xu Jiahong1Xiao Zhenjiu2
1(School of Software,Liaoning Technical University,Huludao 125105,Liaoning,China)2(School of Computer,Communication University of China,Beijing 100024,China)
AbstractTo solve the security problem in existing ID-based authenticated key agreement protocol, in this paper we propose an improved ID-based authenticated key agreement protocol. The protocol uses bilinear pairing operation method, combines the temporary and long-term private keys of both users sides to calculate the final session key, and solves the problem of PKG-forward security in previous protocol, the problem caused by singly depending on the temporary or long-term private keys, and the problem of known temporary session key leakage attacks. Based on ensuring the correctness of the improved protocol, we analyse the security attribute and the performance of the improved protocol, and carry out formal analysis on the protocol with SVO logic, as well as verify the authentication property and security of the improved protocol. Results show that it satisfies all the security requirements of an ID-based authenticated key agreement protocol. Comparing with other existing similar protocols, it has better safety attribute and higher computational efficiency.
KeywordsID-based authenticationKey agreementBilinear pairingSVO logicFormal verification
0引言
密鑰協(xié)商協(xié)議作為最基礎(chǔ)的密碼原語(yǔ)之一,旨在在敵手控制的非安全信道中,兩個(gè)或多個(gè)通信用戶(hù)交換信息,用戶(hù)間彼此認(rèn)證對(duì)方的身份,并協(xié)商出一個(gè)共享的會(huì)話(huà)密鑰。所協(xié)商出的會(huì)話(huà)密鑰可在將來(lái)的通信會(huì)話(huà)中使用,且對(duì)通信系統(tǒng)中傳輸?shù)臄?shù)據(jù)提供機(jī)密性和認(rèn)證性等服務(wù)。
Diffie和Hellman[1]提出了第一個(gè)對(duì)等環(huán)境下的密鑰協(xié)商協(xié)議,而基本的Diffie-Hellman協(xié)議并不提供通信雙方的認(rèn)證,因而存在中間人攻擊的安全問(wèn)題。1984年,Shamir[2]基于公鑰提出了第一個(gè)基于身份的密鑰協(xié)商協(xié)議(ID-AKA),這一協(xié)議的提出減去了繁瑣的證書(shū)發(fā)放和管理機(jī)制。2001年,由Boneh等人[3]第一個(gè)提出利用雙線(xiàn)性對(duì)運(yùn)算的基于身份的認(rèn)證密鑰協(xié)商協(xié)議,但該協(xié)議卻不能保證前向安全性。隨后,又出現(xiàn)了許多基于雙線(xiàn)性對(duì)運(yùn)算的協(xié)議,如文獻(xiàn)[4-5,9-12]等。1997年,Blake-Wilson等人在文獻(xiàn)[8]中提出了基于RSA環(huán)境下的AKA協(xié)議的BJM97模型。而在此環(huán)境下BJM97模型不能保證前向安全性,且在測(cè)試會(huì)話(huà)中,Corrupt查詢(xún)不能被進(jìn)行,而且還不能抵抗密鑰泄露模仿攻擊。之后Chen等人在文獻(xiàn)[13,14]中,定義并發(fā)展了基于身份的認(rèn)證密鑰協(xié)商協(xié)議安全模型 ID-BJM模型,目前絕大部分關(guān)于ID-AKA協(xié)議,如文獻(xiàn)[4-7,13-16],都是在BJM修改模型下給出安全性證明。
2007年,王圣寶等[15]提出了帶有會(huì)話(huà)密鑰托管的基于身份的認(rèn)證密鑰協(xié)商協(xié)議(簡(jiǎn)稱(chēng)WCD-1協(xié)議)和無(wú)會(huì)話(huà)密鑰托管的基于身份的認(rèn)證密鑰協(xié)商協(xié)議(簡(jiǎn)稱(chēng)WCD-2協(xié)議),并在ID-BJM模型下對(duì)兩個(gè)協(xié)議進(jìn)行了證明;之后汪小芬等人[16]對(duì)WCD-2協(xié)議進(jìn)行了分析和改進(jìn),提出了改進(jìn)后的協(xié)議(簡(jiǎn)稱(chēng)WCX協(xié)議),但改進(jìn)后的協(xié)議仍不滿(mǎn)足已知會(huì)話(huà)相關(guān)臨時(shí)秘密信息安全屬性。而此類(lèi)文獻(xiàn)中,均是在標(biāo)準(zhǔn)模型下證明協(xié)議的安全,并未給出形式化的證明分析,如文獻(xiàn) [15-21]。因此本文在WCD-2協(xié)議的基礎(chǔ)上,提出改進(jìn)的協(xié)議,權(quán)衡了安全性質(zhì)和計(jì)算效率這兩者的關(guān)系,增加了密鑰確認(rèn)機(jī)制。通過(guò)SVO邏輯對(duì)改進(jìn)的協(xié)議進(jìn)行形式化分析證明,使協(xié)議具有更好的安全性。
1雙線(xiàn)性對(duì)和困難問(wèn)題假設(shè)
定義1設(shè)G1、G2分別為階數(shù)是q的循環(huán)加法群和乘法群,e:G1×G1→G2中的e為雙線(xiàn)性對(duì)的一個(gè)映射,它擁有如下性質(zhì):
(1) 雙線(xiàn)性:若g,h∈G1且a,b∈Zq,存在e(ag,bh)=e(g,h)ab。
(2) 非退化性:若g∈G1,則e(g,g)≠1。
(3) 可計(jì)算性:若g,h∈G1,則存在有效的算法可計(jì)算e(g,h)。
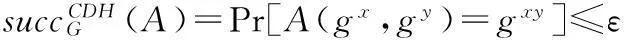
2WCD-2協(xié)議及安全性分析
2.1WCD-2協(xié)議簡(jiǎn)介
1) 系統(tǒng)建立

2) 私鑰生成
對(duì)應(yīng)身份ID∈Zq,從PKG中隨機(jī)選擇rID∈Zq,且每一個(gè)身份ID,均固定rID,計(jì)算私鑰dID=[rID,hID],且hID=(hg-rID)1/(α-ID)。
3) 密鑰協(xié)商
設(shè)密鑰協(xié)商的雙方分別為Alice和Bob,Alice的身份為IDA,私鑰為hA,Bob的身份為IDB,私鑰為hB。Alice、Bob的公鑰分別為 gA=g1g-IDA、gB=g1g-IDB,Alice和Bob進(jìn)行會(huì)話(huà)密鑰協(xié)商,其中g(shù)T=e(g,g)為公開(kāi)參數(shù)。

(2) Alice將接收到的TB=TB1‖TB2‖TB3,計(jì)算出共享秘密KAB1和KAB2,然后Alice計(jì)算會(huì)話(huà)密鑰SKAB=H(IDA‖IDB‖TA‖TB‖KAB1‖KAB2);接著B(niǎo)ob將接收的TA=TA1‖TA2‖TA3,計(jì)算共享秘密KBA1和KBA2,最后Bob計(jì)算會(huì)話(huà)密鑰SKBA=H(IDA‖IDB‖TA‖TB‖KBA1||KBA2)。
(3) 根據(jù)雙線(xiàn)性對(duì)的性質(zhì),得出Alice與Bob計(jì)算出的會(huì)話(huà)密鑰為SK=H(IDA‖IDB‖TA‖TB‖e(g,h)x+y‖e(g,t)xy)。
2.2WCD-2協(xié)議安全性分析
(1) 若存在攻擊者C,攻擊并獲取PKG主私鑰α,則會(huì)出現(xiàn)以下攻擊情況:
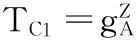
KAB1=e(TC1,hA)(TC2)rAe(g,h)x=e(g,h)x+z
由于攻擊者C獲取了PKG主私鑰α,由=g(α-IDB).x=(gx)α-IDB,可計(jì)算出gx,繼而計(jì)算出共享密鑰:
KCA1=e(gx,h)·e(g,h)z=e(g,h)x+z
協(xié)議執(zhí)行后,C成功冒充B與A進(jìn)行協(xié)商,并獲得了一個(gè)會(huì)話(huà)密鑰SK。
(2) 若攻擊者C獲取主私鑰α和發(fā)送方A的長(zhǎng)期私鑰dA=[rA,hA],則會(huì)根據(jù)(1)的基礎(chǔ)上繼續(xù)進(jìn)行如下運(yùn)算:
=e(g,ht-rA)z(α-IDB)/(α-IDA)·e(g,t)zrA·e(g,h)x
協(xié)議執(zhí)行后,C成功冒充B與A進(jìn)行協(xié)商,并獲得了一個(gè)最終的會(huì)話(huà)密鑰SK。
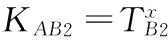
3改進(jìn)的WCD-2協(xié)議
3.1系統(tǒng)建立

3.2私鑰生成
對(duì)應(yīng)身份ID∈Zq,隨機(jī)選擇rID∈Zq,且每一個(gè)身份ID,均固定rID,計(jì)算私鑰dID=[rID,hID],且hID=(hg-rID)1/(α-ID)。
3.3密鑰協(xié)商與認(rèn)證
設(shè)用戶(hù)分別為發(fā)送方A和響應(yīng)方B,且發(fā)送方A的身份為IDA,私鑰為dA,響應(yīng)方B的身份為IDB,私鑰為dB。發(fā)送方A和響應(yīng)方B進(jìn)行會(huì)話(huà)密鑰協(xié)商。令gA=g1g-IDA,gB=g1g-IDB,t=e(g,h)和gT=e(g,g),身份ID對(duì)應(yīng)的公鑰為gID,發(fā)送方A和響應(yīng)方B可分別預(yù)先計(jì)算出gA、gB、t。
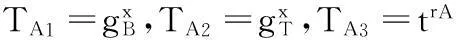
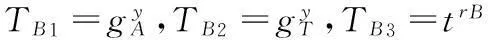
(3) 發(fā)送方A接受到TB=TB1‖TB2‖TB3,并計(jì)算共享秘密KAB=[e(TB1,hA)(TB2)rA(TB3)]x+rA,同理響應(yīng)方B接收到TA=TA1‖TA2‖TA3,計(jì)算共享秘密KBA=[e(TA1,hB)(TA2)rB(TA3)]y+rB;
(4) 發(fā)送方A根據(jù)共享密鑰,計(jì)算會(huì)話(huà)密鑰SKAB=H(IDA‖IDB‖TA‖TB‖KAB),同理響應(yīng)方B根據(jù)共享密鑰,計(jì)算會(huì)話(huà)密鑰SKBA=H(IDA‖IDB‖TA‖TB‖KBA);
(5) 發(fā)送方A和響應(yīng)方B互相確認(rèn)身份,根據(jù)雙線(xiàn)性對(duì)的性質(zhì),容易得出發(fā)送方A和響應(yīng)方B共享的會(huì)話(huà)密鑰為SK=H(IDA‖IDB‖TA‖TB‖e(g,h)xy+xrA+yrB+rArB)。
發(fā)送方A與響應(yīng)方B之間的基于身份的認(rèn)證密鑰協(xié)商協(xié)議如圖1所示。

圖1 改進(jìn)的基于身份的認(rèn)證密鑰協(xié)商協(xié)議過(guò)程
3.4改進(jìn)協(xié)議的正確性分析
(1) 首先根據(jù)已知條件,可計(jì)算出響應(yīng)方B的TB1值:
(2) 其次根據(jù)雙線(xiàn)性對(duì)的性質(zhì),計(jì)算e(TB1,hA):
=e(gy,h)e(gy,g-rA)
=e(g,h)ye(g,g)-rAy
(3) 再結(jié)合已知條件,計(jì)算出KAB的值:
KAB=[e(TB1,hA)(TB2)rA(TB3)]x+rA
=[e(g,h)ye(g,g)-rAye(g,g)rAye(g,h)rB]x+rA
=[e(g,h)y+rB](x+rA)
(4) 同理可得TA1,e(TA1,hB),KBA的值,其中:
KBA=[e(TA1,hB)(TA2)rB(TA3)]y+rB
=[e(g,h)xe(g,g)-rBxe(g,g)rBxe(g,h)rA]y+rB
=[e(g,h)x+rA](y+rB)
所以:
SKBA=H(IDA‖IDB‖TA‖TB‖KBA)
=H(IDA‖IDB‖TA‖TB‖KAB)
=SKAB
最終可證:
SK=H(IDA‖IDB‖TA‖TB‖e(g,h)xy+xrB+yrA+rArB)
3.5改進(jìn)協(xié)議中的密鑰確認(rèn)
由WCD-2協(xié)議的消息流可以看出, 發(fā)送方A與響應(yīng)方B之間缺少相互的認(rèn)證機(jī)制。若攻擊者E通過(guò)攔截并獲得A的消息后, 可以假裝成B生成消息并發(fā)送給A且不被A發(fā)現(xiàn)。若協(xié)議參與者繼續(xù)執(zhí)行, 且生成一個(gè)會(huì)話(huà)密鑰, 攻擊者E還可以利用自己攻擊獲得來(lái)的信息,生成一致的會(huì)話(huà)密鑰, 從而最終與發(fā)送方A 建立一個(gè)共享的會(huì)話(huà)密鑰。為了解決上述存在的冒充攻擊問(wèn)題,在本節(jié)中采用對(duì)稱(chēng)加密的方法為改進(jìn)協(xié)議增加密鑰確認(rèn)機(jī)制。
改進(jìn)協(xié)議的密鑰確認(rèn)過(guò)程如圖2所示。
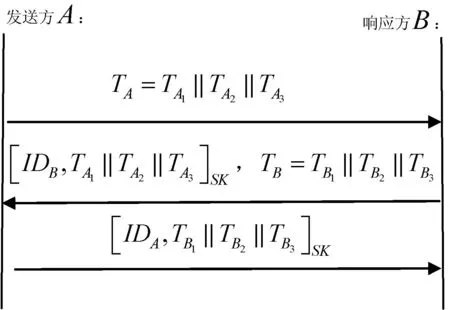
圖2 改進(jìn)協(xié)議的密鑰確認(rèn)過(guò)程
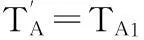
3.6改進(jìn)協(xié)議的安全屬性分析
協(xié)議的安全屬性分析主要有以下幾個(gè)方面:
(1) 已知會(huì)話(huà)密鑰安全性。改進(jìn)協(xié)議中臨時(shí)密鑰選取的是隨機(jī)數(shù)x、y,每當(dāng)改進(jìn)協(xié)議執(zhí)行一次時(shí),都要從發(fā)送方A,響應(yīng)方B中隨機(jī)選取一次,因此多個(gè)會(huì)話(huà)密鑰之間不具有相關(guān)性。
(2) 前向安全性。即使發(fā)送方A和接收方B,其中一方或者兩者同時(shí)都泄露了長(zhǎng)期密鑰dID=
(3)PKG前向安全性。攻擊者E攻擊PKG獲得α,但仍無(wú)法計(jì)算發(fā)送方A和響應(yīng)方B的會(huì)話(huà)密鑰,因?yàn)楣粽逧通過(guò)所掌握的信息能夠計(jì)算出:
即可以計(jì)算出:gx、gy,但仍然無(wú)法計(jì)算出e(g,h)xy,因?yàn)檫@需要解決CDH困難問(wèn)題,繼而也無(wú)法計(jì)算出共享秘鑰KAB=KBA=e(g,h)xy+rBx+rAy+rArB,因此改進(jìn)協(xié)議具有PKG前向安全性。
(4) 抗密鑰泄露偽裝攻擊。假設(shè)攻擊者E得知發(fā)送方A泄露的長(zhǎng)期密鑰并偽裝成A,但E不可能成功地偽裝成響應(yīng)方B并與發(fā)送方A進(jìn)行密鑰協(xié)商,因?yàn)镋并不知道B的私鑰,因此無(wú)法計(jì)算出相應(yīng)的會(huì)話(huà)密鑰。
(5) 密鑰完整性。最終會(huì)話(huà)密鑰的形成是由發(fā)送方A和響應(yīng)方B兩者隨機(jī)所選擇的x、y值和其長(zhǎng)期密鑰決定的。因此雙方都無(wú)法預(yù)先決定選擇的值,對(duì)于攻擊者E而言,即使它采用中間人攻擊,也無(wú)法使得A、B、E三者的會(huì)話(huà)密相同,因而改進(jìn)協(xié)議滿(mǎn)足密鑰完整性。
(6) 已知會(huì)話(huà)臨時(shí)密鑰安全性。攻擊者E即使得知發(fā)送方A和響應(yīng)方B的臨時(shí)密鑰x、y值,但最終的會(huì)話(huà)密鑰值是由臨時(shí)密鑰x、y和長(zhǎng)期密鑰中rIDA和rIDB構(gòu)成的,因此無(wú)法計(jì)算出e(g,h)xy,甚至e(g,h)xy+rBx+rAy+rArB,所以改進(jìn)協(xié)議具有已知會(huì)話(huà)臨時(shí)密鑰安全性。
(7) 抗未知密鑰共享。發(fā)送方A和響應(yīng)方B在協(xié)商會(huì)話(huà)密鑰時(shí),發(fā)送方A不會(huì)被強(qiáng)制與第三方C進(jìn)行共享會(huì)話(huà)密鑰協(xié)商。因?yàn)樵谛畔⒔换サ倪^(guò)程中,A發(fā)送的信息是用B的公鑰進(jìn)行加密的,因此C無(wú)法計(jì)算出相應(yīng)的會(huì)話(huà)密鑰。
4改進(jìn)協(xié)議的形式化分析
形式化邏輯分析語(yǔ)言SVO吸收了BAN、GNY、AT等邏輯系統(tǒng)的優(yōu)點(diǎn),具有十分簡(jiǎn)潔的推理規(guī)則和公理。在形式化語(yǔ)義方面,SVO邏輯對(duì)一些概念進(jìn)行了重新定義,本文以協(xié)議的假設(shè)為起點(diǎn),運(yùn)用邏輯推理規(guī)則得到最終實(shí)現(xiàn)的目標(biāo),從而證明協(xié)議的安全性。
4.1SVO邏輯語(yǔ)法符號(hào)
(1) P says X:表示此次會(huì)話(huà)開(kāi)始后P發(fā)送了消息X。
(2) P said X:表示以前會(huì)話(huà)P發(fā)送了消息X。
(3) P sees X:表示P擁有消息X。
(4) {Xp}K:用密鑰K對(duì)消息X加密后得到的消息,P為發(fā)送者(常省略)。
(5) [X]K:用私鑰K對(duì)消息X簽名后得到的消息,并自動(dòng)獲得了X。
(6) K-1:表示密鑰K對(duì)應(yīng)的解密密鑰。
(7) PKψ(P,K):表示K是P的加密公鑰。
(8) PKσ(P,K):表示K是P的簽名驗(yàn)證公鑰。
(9) PKδ(P,K):表示K是P的協(xié)商公鑰,并且公鑰所對(duì)應(yīng)的私鑰是良好的。
(10) SV(X,K,Y):表示簽名驗(yàn)證,即對(duì)于簽名X,用簽名驗(yàn)證密鑰K驗(yàn)證X是否為消息Y的簽名。
(11) ShareKey(K,P,Q):表示K是P與Q的良好共享密鑰。
(12) ShareKey(K-,P,Q):表示P與Q通信中密鑰K未得到確認(rèn),此為非確認(rèn)共享密鑰,即ShareKey(K-,P,Q)=(ShareKey(K,P,Q))∧(PseesK)。
(13) ShareKey(K+,P,Q):表示P與Q通信中密鑰K得到確認(rèn),此為確認(rèn)共享密鑰,即ShareKey(K+,P,Q)=(ShareKey(K,P,Q))∧(PseesK)∧(Qsays(QseesK))。
(14) *:SVO使用*表示主體所收到的但不可識(shí)別的消息。
4.2SVO推理規(guī)則及公理
4.2.1SVO的兩個(gè)初始規(guī)則
1) 分離規(guī)則
MP(Modus Ponens):φ∧φ?ψ?ψ
2) 必要性規(guī)則
Nec(Necessitation):├φ?├Pbelievesφ
4.2.2SVO的11條公理
1) 相信公理
Ax0 (Pbelievesφ∧Pbelievesψ)≡(Pbelievesψ∧ψ)
Ax1 Pbelievesφ∧Pbelieves(φ?ψ)?Pbelievesψ
Ax2 Pbelievesφ?Pbelieves(Pbelievesφ)
2) 源關(guān)聯(lián)公理
Ax3 SharedKey(K,P,Q)∧Rreceived{XQ}K?QsaidX∧QseesK
Ax4 PKσ(Q,K)∧RreceivedX∧SV(X,K,Y)?QsaidY
3) 密鑰協(xié)商公理
Ax5 PKδ(P,Kp)∧PKδ(Q,Kq)?SharedKey(F0(Kp,KQ),P,Q)
Ax6 φ≡φ[F0(K,K′)/F0(K′,K)]
公理Ax5中F0(Kp,KQ)表示協(xié)商密鑰生成函數(shù)(如DH算法),F(xiàn)0使用第1個(gè)參數(shù)所表示的公鑰,使用第2個(gè)參數(shù)所對(duì)應(yīng)的私鑰。
4) 接收公理
Ax7 Preceived(X1,…,Xn)?PreceivedXi
Ax8 Preceived{X}k∧PseesK-1?PreceivedX
Ax9 Preceived[X]k?PreceivedX
5) 看見(jiàn)公理
Ax10 PreceivedX?PseesX
Ax11 Psees(X1,…,Xn)?PseesXi
Ax12 PseesX1∧…∧PseesXn?PseesF(X1,…,Xn)
6) 理解公理
Ax13 Pbelieves(PseesF(X))?Pbelieves(PseesX)
7) 說(shuō)過(guò)公理
Ax14 Psaid(X1,…,Xn)?PsaidXi∧PseesXi
Ax15 Psays(X1,…,Xn)?PsaysXi∧Psaid(X1,…,Xn)
公理Ax14表明一個(gè)主體只能說(shuō)它所擁有的,公理Ax15表明一個(gè)主體最近說(shuō)過(guò)且包含它說(shuō)過(guò)的。
8) 仲裁公理
Ax16 Pcontrolsφ∧Psaysφ?φ
公理Ax16表明P對(duì)φ有仲裁權(quán)。
9) 新鮮性公理
Ax17 fresh(Xi)?fresh(X1,…,Xn)
Ax18 fresh(X1,…,Xn)?fresh(F(X1,…,Xn))
公理Ax18中,F(xiàn)的計(jì)算必須依賴(lài)X1,…,Xn中新鮮元素的值,若F(X1,X2,X3)=(X1+(0*X2)+X3)不是新鮮的,因?yàn)镕的計(jì)算并不依賴(lài)于X2的值,即公理Ax18不可用。
10) Nonce驗(yàn)證公理
Ax19 fresh(X)∧PsaidX?PsaysX
11) 共享密鑰對(duì)稱(chēng)公理
Ax20 SharedKey(K,P,Q)≡SharedKey(K,Q,P)
公理Ax20表明共享密鑰具有對(duì)稱(chēng)性。
根據(jù)SVO邏輯中的Ax1公理和MP法則,可得到以下結(jié)論:
P|≡φ∧P|≡φ?ψ|-P|≡ψ
4.3改進(jìn)協(xié)議的SVO邏輯分析過(guò)程
運(yùn)用SVO邏輯來(lái)證明新協(xié)議的安全過(guò)程如下:首先用SVO邏輯語(yǔ)言,表示已給出的協(xié)議初始假設(shè)集,再推導(dǎo)出協(xié)議最后要實(shí)現(xiàn)的目標(biāo)集,最后證明假設(shè)集├目標(biāo)集。結(jié)論成立,則說(shuō)明已經(jīng)達(dá)到了協(xié)議預(yù)期的設(shè)計(jì)目標(biāo),由此可知協(xié)議是安全的。
首先,根據(jù)協(xié)議的內(nèi)容,對(duì)發(fā)送方A的關(guān)于密鑰協(xié)商初始的建設(shè),信息接收和論證的過(guò)程的假設(shè)(響應(yīng)方B的初始假設(shè)也這樣類(lèi)似得到):
G1 A believes fresh(x)∧(A sees x)
G2 A believes PKδ(A,x)
G3 A believes Bseesy
G4 A believes A received(gag-IDB)x
G5 A believes A received{IDB,TA1‖TA2‖TA3}SK
G6 A received[(g,g-IDA)x∧(Bseesy)?PKδ(B,y)]
G7 A believes A received[(g,g-IDA)x∧(Bseesy)?PKδ(B,y)]
G8 A believes A received{IDB,TA1‖TA2‖TA3}SK
然后,再用SVO邏輯來(lái)表示協(xié)議的實(shí)現(xiàn)目標(biāo)發(fā)送方A實(shí)現(xiàn)的目標(biāo)集為:
A believes ShareKey(K+,A,B),A believes fresh(SK);
響應(yīng)方B實(shí)現(xiàn)的目標(biāo)集為:
B believes ShareKey(K+,A,B),B believes fresh(SK)。
最后,由上述假設(shè)和SVO邏輯(下面同4.1節(jié)的符號(hào)表示)的公理及規(guī)則,對(duì)協(xié)議進(jìn)行如下的推理和證明:
A believes (A received (gag-IDB)x∧Bseesb)
由G3、G4、公理Ax0可得。
(1) A believes PKδ(B,b)由SVO邏輯(1)、G6、公理Ax0、Ax1+MP規(guī)則可得。
(2) A believes(PKδ(A,x)∧PKδ(B,b))由G2、(2)、公理Ax0可得。
(3) A believes(PKδ(A,x)∧PKδ(B,b)?ShareKey(K,A,B))SK=(IDA‖IDB‖TA‖TB‖e(g,h)(x+rA)(y+rB))由(3)、公理Ax5可得。
(4) A believes ShareKey(K,A,B)由(3)、(4)、Ax1+MP規(guī)則可得。
(5) A believes(AseesSK)∧(Bsaid(BseesSK))由G5、G7、公理Ax0、Ax1+MP規(guī)則可得。
(6) A believes(AseesSK)由(6)、公理Ax0可得。
(7) A believes Bsaid(BseesSK)由(6)、公理Ax0可得。
(8) A believes Bsaid(BseesSK)由(6)、公理Ax0可得。
(9) A believes fresh(x)?fresh(IDA‖IDB‖TA‖TB‖e(g,h)(x+rA)(y+rB))由G1和公理Ax18可得。
(10)Abelievesfresh(IDA‖IDB‖TA‖TB‖e(g,h)(x+rA)(y+rB)),即Abelievesfresh(SK)由G1、(9)、公理Ax0、A1+MP規(guī)則可得。
(11) A believes Bsays(BseesSK)由(8)、(10)、公理Ax19可得。
(12)Abelieves(ShareKey(K,A,B)∧(AseesSK)∧Bsaid(BseesSK))即AbelievesShareKey(K+,A,B)由(5)、(7)、(11)、公理Ax0可得。
最終分析結(jié)果為:A believes ShareKey(K+,A,B),A believes fresh(SK)。
同理,響應(yīng)方B也可以通過(guò)上述方法,得到最后的結(jié)論。根據(jù)上述的證明結(jié)果,協(xié)議成功執(zhí)行后,發(fā)送方A和響應(yīng)方B都相信SK是它們雙方確認(rèn)通信的共享密鑰,并且該密鑰是新鮮的。運(yùn)用SVO邏輯對(duì)協(xié)議進(jìn)行形式化證明分析,新協(xié)議達(dá)到了預(yù)先設(shè)定的目標(biāo)集,由此證明新協(xié)議是安全的。
5協(xié)議的性能分析比較
協(xié)議的性能分析主要從安全性和計(jì)算效率兩方面進(jìn)行分析比較。現(xiàn)將文獻(xiàn)[15]和文獻(xiàn)[16]中的幾個(gè)協(xié)議與改進(jìn)協(xié)議(簡(jiǎn)稱(chēng)NEW協(xié)議)的安全性和計(jì)算效率進(jìn)行比較,比較結(jié)果如表1和表2所示。

表1 協(xié)議的安全性的比較

表2 協(xié)議的計(jì)算效率比較
其中,F(xiàn)S代表前向安全性;PKG-FS代表PKG前向安全性;KSK代表已知會(huì)話(huà)密鑰安全性;KI代表密鑰完整性;Y、N分別代表表中對(duì)應(yīng)的協(xié)議是否滿(mǎn)足相應(yīng)的安全性。
通過(guò)表1的比較結(jié)果可以看出,改進(jìn)協(xié)議與同類(lèi)文獻(xiàn)中的協(xié)議相比,改進(jìn)協(xié)議均滿(mǎn)足上述安全屬性的需求。
其中,Pairing Computation雙線(xiàn)性運(yùn)算簡(jiǎn)稱(chēng)為P;Multiplication Computation乘法運(yùn)算簡(jiǎn)稱(chēng)為M;Index Computation指數(shù)運(yùn)算簡(jiǎn)稱(chēng)為S。
通過(guò)表2的比較結(jié)果可以看出,改進(jìn)協(xié)議與同類(lèi)文獻(xiàn)中的協(xié)議相比,并沒(méi)有明顯增加計(jì)算負(fù)擔(dān)。
綜上所述,從表1和表2的結(jié)果和3.6節(jié)中的安全屬性分析可以看出,改進(jìn)協(xié)議滿(mǎn)足目前所有安全性能的指標(biāo),并且較好地權(quán)衡了安全性和計(jì)算效率這兩者的關(guān)系。
6結(jié)語(yǔ)
本文在文獻(xiàn)[15]中的WCD-2協(xié)議的基礎(chǔ)上,針對(duì)其存在的不安全因素,提出了改進(jìn)的協(xié)議。解決了WCD-2協(xié)議中存在的PKG前向安全性的問(wèn)題,以及由于單一依賴(lài)臨時(shí)或長(zhǎng)期私鑰,而不具備已知會(huì)話(huà)臨時(shí)密鑰安全性的問(wèn)題。最后,在改進(jìn)協(xié)議的基礎(chǔ)上,增加了密鑰確認(rèn)機(jī)制,使協(xié)議更安全地實(shí)現(xiàn)了基于身份的認(rèn)證。同時(shí)本文通過(guò)SVO邏輯對(duì)改進(jìn)協(xié)議進(jìn)行形式化分析,驗(yàn)證了協(xié)議的安全性。在協(xié)議性能分析方面,較好地權(quán)衡了安全性質(zhì)和計(jì)算效率的這兩者的關(guān)系,使改進(jìn)后的協(xié)議更具有實(shí)際的意義。
參考文獻(xiàn)
[1] Diffie W,Hellman M E.New directions in cryptography[J].IEEE Trans Info Theory,1976,22(6):44-654.
[2] Shamir A.Identity-based cryptosystems and signature schemes[C]//Advances in Cryptology—Crypto1984,Berlin:Springer-Verlag,1984:47-53.
[3] Boneh D,Franklin M.Identity based encryption from the Weil pairing[C]//Advances in Cryptology—Crypto 2001,Berlin:Springer-Verlag,2001:213-229.
[4] Yuan Q,Li S.A new efficient ID-based authenticated key agreement protocol[EB/OL].2011-6-5.(2005-08-29).[2009-08-25].http://Cryptology ePrint Archive2005/309.
[5] Ni L,Chen G,Li J,et al.Strongly secure identity-based authenticated key agreement prot ocols[J].Computers and Electrical Engineering,2011,37(2):205-217.
[6] Cao X,Kou W,Du X.A pairing-free identity-based authenticated key agreement protocol with mimimal message exchanges[J].Information Sciences,2010,180(15):2895-2903.
[7] He D,Chen J,Hu J.A new provably secure authenticated key agreement protocol without blinear pairings[J].JOURNAL of Information & Computartional Science,2010,7(5):1089-1096.
[8] Blakewlson S,Johnson C,Menezes A.Key agreement protocols and their security analysis[C]//Proceedings of the 6th IMA International Conference on Cryptography and Coding,Berlin,1997:30-45.
[9] 王璐,侯林峰,張耀武.一種改進(jìn)的雙線(xiàn)性對(duì)的雙向基于身份的認(rèn)證密鑰協(xié)商協(xié)議[J].信息通信,2012(1):129-130.
[10] 張文科,李芳.基于身份的增強(qiáng)三方認(rèn)證密鑰協(xié)商協(xié)議[J].計(jì)算機(jī)工程與應(yīng)用,2013,49(15):92-96.
[11] 項(xiàng)順伯.一種基于雙線(xiàn)性對(duì)的三方密鑰交換協(xié)議[J].廣東石油化工學(xué)院學(xué)報(bào),2013,23(1):34-36.
[12] 劉志遠(yuǎn).安全的基于身份認(rèn)證密鑰協(xié)商協(xié)議[J].湖南科技大學(xué)學(xué)報(bào),2014,29(1):64-67.
[13] Chen L,Kulda C.Identity based authenticated key agreement protocols from pairing[C]//Proceedings of 16th IEEE Computer Security Foundations Workshop,New York,2003:219-233.
[14] Chen L,Cheng Z,Smart N P.Identity-based Key Agreement Protocols from Pairings[J].International Journal of Information Security,2007,6(4):213-241.
[15] 王圣寶,曹珍富,董曉蕾.標(biāo)準(zhǔn)模型下可證安全的身份基認(rèn)證密鑰協(xié)商協(xié)議[J].計(jì)算機(jī)學(xué)報(bào),2007,30(10):1842-1852.
[16] 汪小芬,陳原,肖國(guó)鎮(zhèn).基于身份的認(rèn)證密鑰協(xié)商協(xié)議的安全性分析與改進(jìn)[J].通信學(xué)報(bào),2008,29(12):16-21.
[17] 項(xiàng)順伯.基于身份的改進(jìn)認(rèn)證密鑰協(xié)商協(xié)議[J].計(jì)算機(jī)工程,2011,37(17):128-129.
[18] 舒劍.高效的強(qiáng)安全的基于身份認(rèn)證密鑰協(xié)商協(xié)議[J].計(jì)算機(jī)應(yīng)用,2012,32(1):95-98.
[19] 高海英.高效的基于身份的認(rèn)證密鑰協(xié)商協(xié)議[J].計(jì)算機(jī)應(yīng)用,2012,32(1):35-37.
[20] 李芳,陳明.強(qiáng)安全的和無(wú)雙線(xiàn)性對(duì)的基于身份密鑰協(xié)商[J].計(jì)算機(jī)工程與科學(xué),2013,35(6):65-71.
[21] 高海英.可證明安全的基于身份的認(rèn)證密鑰協(xié)商協(xié)議[J].計(jì)算機(jī)研究與發(fā)展,2012,49(8):1685-1689.
中圖分類(lèi)號(hào)TP309
文獻(xiàn)標(biāo)識(shí)碼A
DOI:10.3969/j.issn.1000-386x.2016.02.066
收稿日期:2014-08-06。國(guó)家自然科學(xué)基金項(xiàng)目(61103199)。陳虹,副教授,主研領(lǐng)域:網(wǎng)絡(luò)安全。徐嘉鴻,碩士生。肖振久,副教授。

