四點式起落架飛機地面滑跑轉彎分析

茍能亮，苑強波，張明

(1.南京航空航天大學 飛行器先進設計技術國防重點學科實驗室，南京　210016)

(2.沈陽飛機設計研究所 結構設計部，沈陽　110035)

?

四點式起落架飛機地面滑跑轉彎分析

茍能亮1，苑強波2，張明1

(1.南京航空航天大學 飛行器先進設計技術國防重點學科實驗室，南京210016)

(2.沈陽飛機設計研究所 結構設計部，沈陽110035)

摘要：現代飛機對其地面滑跑性能的要求日益提高，同時要求能夠在條件更加苛刻的環境下運行。以四點式起落架布局飛機為研究對象，基于阿克曼轉向幾何原理，推導該飛機地面滑跑時兩個前輪之間的轉角關系。在Adams/Aircraft中建立四點式起落架飛機虛擬樣機，并進行其地面滑跑仿真分析。探討四點式起落架飛機不同前輪作為主動操縱輪時，對轉彎半徑的影響。結果表明：在相同滑跑條件下，當前輪操縱轉彎時，四點式起落架飛機比常規的前三點式起落架飛機擁有更小的轉彎半徑；當主輪差動剎車轉彎時，四點式起落架飛機的轉彎半徑略大于三點式起落架飛機；四點式起落架飛機的兩前輪同時為主動操縱輪時，飛機的轉彎半徑最小。

關鍵詞：四點式起落架；前輪操縱；差動剎車；轉彎半徑

0引言

現代飛機對其在地面滑跑的性能要求日益提高，同時也要求能夠在條件更為苛刻的環境下運行。例如，為了適應未來戰場環境，要求軍用飛機能夠在簡單修復或泥土道面起降[1]；為了減少對跑道的占用，要求現代民用飛機能夠高速滑離跑道并轉入滑行道[2]。

國外，S.H.Goldthorpe等[2]研究了飛機高速滑離跑道并轉入滑行道(ROTO)時對跑道的占用時間,提出了對前輪轉向和差動剎車的要求。通過建立三自由度的運動方程(航向、側向和偏航)，在模型中加入了前輪自動駕駛轉向模塊和防滑剎車模塊。A.G.Barnes等[3]總結了飛機地面操縱仿真的研究情況，分析了某些關鍵因素對飛機地面操縱運動品質的影響。

國內，顧宏斌[4]建立了機體為六自由度的可操縱飛機地面運動數學模型。該模型只要給定操縱信號，就能求出前輪和飛機的運動及其相互作用。朱天文[5]研究了具有前輪操縱系統的飛機，給出了飛機地面操縱轉彎半徑和轉彎速度的計算方法, 并分析了飛機地面操縱轉彎半徑與轉彎速度之間的關系。

現有對飛機地面滑跑性能研究主要集中在三輪布局的前輪操縱轉彎[6-8]、滑跑穩定性[9]、擺振穩定性等[10]。對四點式起落架飛機研究較少。在國內，羅東等[11]建立了四點式起落架無人機地面運動的動力學方程和運動方程，并對全量非線性模型進行了起飛、著陸時地面滑跑情況的仿真。四點式起落架飛機與常規布局飛機起落架的不同之處在于：機身前部平行安置兩個前起落架，對兩個前起落架分別安裝前輪轉彎作動筒和組合液壓閥，由一套轉彎控制系統進行獨立的驅動。若固定某單套轉彎系統主動驅動，另一套轉彎系統作隨動(即處于減擺狀態)，則飛機分別以左右輪作主動輪的轉彎半徑和轉彎效率均不同。

本文以四點式起落架飛機為研究對象，推導出飛機轉彎時兩前輪轉角關系，建立全機虛擬樣機，探討四點式起落架飛機不同前輪作為主動操縱輪時，對轉彎半徑的影響。

1內外前輪轉彎角度關系

根據阿克曼轉向幾何原理，當四點式起落架飛機轉彎時，為了減少輪胎與地面之間的偏磨，輪胎應該與地面之間保持純滾動的狀態[12]。因此，在不考慮輪胎自身變形的情況下，內外前輪的轉角度應該滿足一定的幾何關系(如圖1所示)，dw為前輪穩距，α1為內側前輪轉角，α2為外側前輪轉角，Sd為前主輪距，l為前支柱到后支柱的距離。

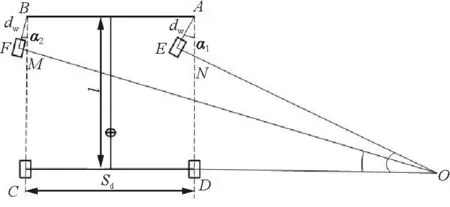
圖1　轉角關系

在ΔMOC中：

(1)

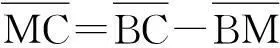
(2)

(3)

由式(1)～式(3)可得

(4)

同理，在ΔNOD中：

(5)

又有

(6)

由式(4)～式(6)可得內外前輪之間的轉角關系：

(7)

2全機虛擬樣機的建立

飛機是一個復雜的多自由度空間運動系統，若考慮所有的自由度，就必須列出相應數量的運動微分方程，使分析和求解變得極為困難，因此必須抓住一些主要的參數及自由度。建立整機的運動方程時，飛機模型不能過于復雜但能較為真實地模擬飛機系統[13]。

2.1基本假設

為了使建立的模型既便于計算，又能較好地模擬真實情況，可對模型作如下假設：

①將飛機分為彈性支撐質量和非彈性支撐質量兩部分，其中彈性支撐質量為緩沖器所支撐的質量，包括機身、機翼、緩沖器外筒等的質量；非彈性支撐質量包括各起落架活塞桿、剎車裝置、機輪以及車架等的質量。彈性支撐質量的運動描述體現在機體的剛體運動方程中，各非彈性支撐質量視為集中質量，具有獨立的運動自由度。

②彈性支撐質量的運動為六自由度的剛體運動，其質量集中于飛機質心處；非彈性支撐質量的運動僅考慮三個方向的平動自由度，其質量集中于機輪或車架與緩沖支柱的連接點處。

③不考慮緩沖支柱的彈性變形。

④各機輪具有獨立的轉動自由度。

⑤飛機的前輪操縱轉彎通常只在低速滑跑時，故不考慮氣動力的影響。

2.2起落架模型

起落架的活塞桿和外筒構成的緩沖器是起落架結構中主要的受力部分。緩沖器軸向力(fs)主要由空氣彈簧力(fa)、油液阻尼力(fd)和摩擦力(ff)組成。在緩沖器全伸長狀態和緩沖器壓縮到最大行程時，fs可由緩沖器結構限制力確定。

fs統一表示為

(8)

式中：Ks為緩沖器拉壓結構限制剛度；S為緩沖器的壓縮行程；Smax為緩沖器最大壓縮行程；S0為緩沖器全伸長狀態時的行程。

S0可表示為

(9)

式中：μm為皮碗當量摩擦系數；Aa為緩沖器氣室有效壓氣面積；P0為緩沖器初始充氣壓力；Patm為當地大氣壓。

空氣彈簧力、油液阻尼力和摩擦力的定義如下：

(1) 空氣彈簧力

(10)

式中：VB0為緩沖器氣腔內初始體積；r為空氣壓縮多變系數，取1.0～1.3。

(2) 油液阻尼力

(11)

式中：ρ為油液密度；Ah為緩沖器有效壓油面積；Ad、Adl分別為正、反行程時主油孔面積；Cd、Cdl分別為正、反行程時主油孔縮流系數；Ahs、Cds分別為回油腔有效壓油面積和油孔縮流系數；An、Anl分別為正、反行程時回油腔油孔總面積。Ad、Adl對于變油孔是隨行程變化的，若有側油孔，則側油孔面積也應包含在內。

(3) 摩擦力

緩沖器內部摩擦力由兩部分組成：①皮碗摩擦力；②由于緩沖支柱彎曲在上下支撐點產生的庫侖摩擦力。

ff=ff1+ff2

(12)

(13)

(14)

式中：μb為庫侖摩擦系數；Nμ、Nl分別為緩沖支柱上下支撐點處產生的正壓力。

2.3輪胎模型

為了更加準確地模擬飛機在操縱前輪轉彎過程中地面對輪胎的作用力，需要建立合理的輪胎模型。本文采用的輪胎模型是Fiala 操縱力輪胎模型，如圖2 所示。

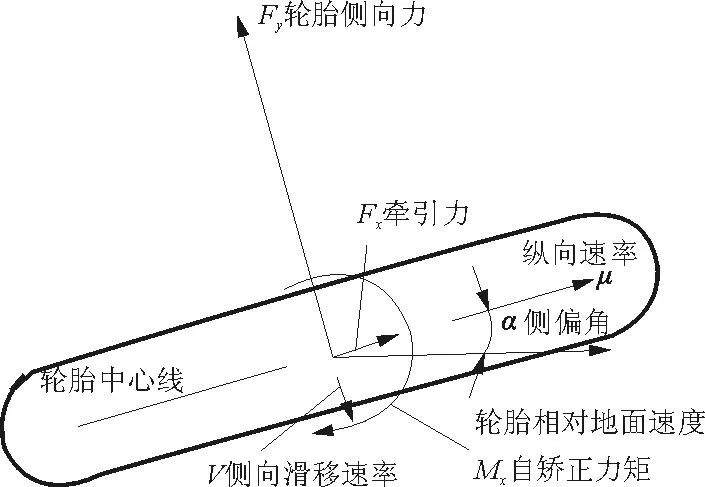
圖2　輪胎模型

輪胎所受地面支反力在機輪坐標系中的定義如下：

(1) 輪胎徑向力

(15)

式中：ε為輪胎壓縮量；f(ε)為輪胎靜壓曲線，可根據試驗數據擬合；CT為輪胎垂直振動當量阻尼系數。

(2) 輪胎縱向力

Fx=μxFz

(16)

式中：μx為航向摩擦系數，與輪胎的航向滑移率相關，本模型采用如下經驗公式計算：

(17)

滑移率Sg定義為

(18)

(19)

式中：rε為輪胎轉動半徑。

(3) 輪胎側向力

側向摩擦力與輪胎的側滑角、側傾角有關。側偏角由機輪速度得出：

(20)

定義轉彎強度N及系數φ：

(21)

(22)

μa為側偏阻力系數，則輪胎側向力可表示為

(23)

N由以下經驗公式給出：

(24)

式中：cε為輪胎偏航系數，主要與輪胎類型有關；p為輪胎額定充氣壓強；pr為輪胎充氣壓強；w為輪胎寬度；d為輪胎自由外徑。

(4) 回正力矩

(25)

(26)

式中：lh為輪胎觸地面半長。

(5) 滾阻力矩

My=μrr0Fz

(27)

式中：μr為滾阻力矩系數。

3轉彎仿真分析

飛機的地面轉彎運動可以采用前輪操縱、主輪的差動剎車或發動機推力差動等技術實現[7]。依據四點式起落架飛機物理參數，采用剛性機身，在Adams/Aircraft中建立的全機虛擬樣機，如圖3所示。在四點式起落架飛機轉彎過程中，將靠近轉彎中心的機輪定義為內側輪，將遠離轉彎中心的機輪定義為外側輪。在模型仿真時，給四點式起落架飛機前輪施加角度驅動，實現飛機的前輪操縱轉彎；給主輪剎車裝置的靜盤和動盤之間施加剎車力矩，實現飛機的差動剎車轉彎。

圖3　四點式起落架飛機虛擬樣機

在對比仿真分析中，定義四點式起落架飛機與三點式起落架飛機擁有相同的前主輪距和主輪距，三點式起落架飛機為前三點式。

3.1不同起落架布局飛機前輪操縱轉彎半徑分析

在給定飛機滑跑速度為30 km/h的條件下，前三點式起落架飛機的前輪轉彎操縱角為10°和四點式起落架飛機內側前輪的轉彎操縱角為10°時，研究兩種不同布局飛機的地面滑跑轉彎半徑。由阿克曼轉向幾何原理可知，四點式起落架飛機內側前輪的轉角大于外側前輪的轉角。因此，當內側輪轉角為10°時，根據式(7)求得外側輪轉角為8.4°。仿真結果如圖4～圖5所示。

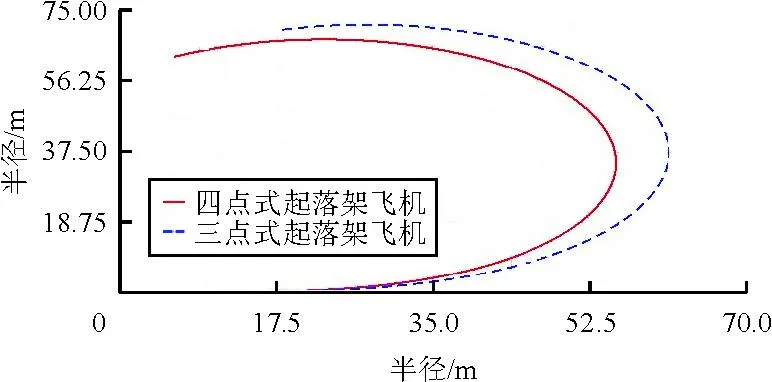
圖4　四點式起落架飛機和三點式起落架飛機的轉彎半徑

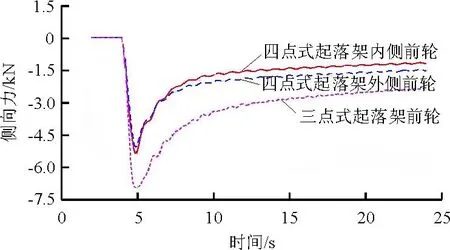
圖5　四點式起落架飛機和三點式起落架飛機

從圖4可以看出：在相同條件下滑跑時，四點式起落架飛機所需的轉彎半徑比三點式起落架飛機的半徑小。飛機在地面操縱轉彎時，主要是由輪胎的側向力對飛機產生偏航力矩而完成整個轉彎過程。側向力過大會導致輪胎的側向變形過大，影響輪胎使用壽命。

從圖5可以看出：在相同速度條件下完成相同轉角的轉彎時，三點式起落架飛機前輪的側向力明顯大于四點式起落架飛機前輪的側向力。四點式起落架飛機在轉彎時，內外前輪分擔了完成轉彎所需的側向力，使分配到每個機輪上的側向力比三點式起落架飛機前輪的側向力小。四點式起落架飛機進入定常轉彎后，外側前輪的側向力比內側前輪的大，是由于飛機在轉彎過程中，機體具有向外滾轉的趨勢，外側起落架支柱產生的軸向力大于內側支柱產生的軸向力，外側輪胎承受的垂向載荷大于內側輪胎承受的垂向載荷。

3.2不同起落架布局飛機主輪差動剎車轉彎半徑分析

在給定飛機滑跑速度為30 km/h的條件下，在外側主輪不施加剎車力矩和內側主輪施加1 000 N·m的剎車力矩時，研究四點式起落架飛機和常規三點式起落架飛機的轉彎半徑。在整個轉彎過程中，所有前輪只受減擺阻尼的影響，處于隨動的減擺狀態。

在主輪差動剎車轉彎時，四點式起落架飛機的轉彎半徑略大于三點式起落架飛機，如圖6所示。

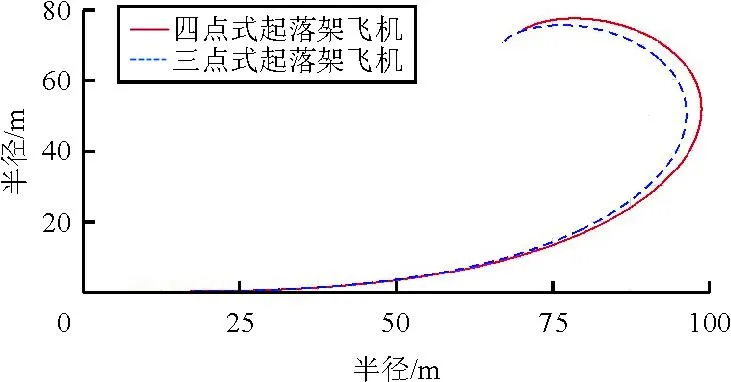
圖6　差動剎車轉彎半徑

差動剎車前輪側向力如圖7所示。

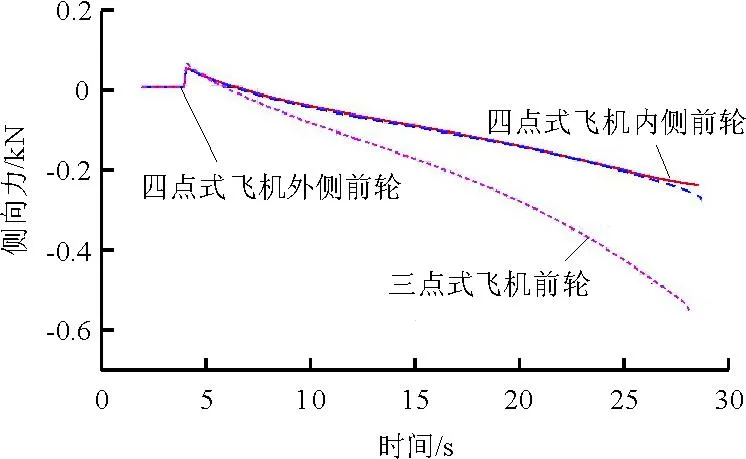
圖7　差動剎車前輪側向力

從圖7可以看出：在差動剎車轉彎的很長時間內(t<25 s)，四點式起落架飛機的內側前輪和外側前輪的側向力大致相等，在此之后(t>25 s)，外側輪的側向力逐漸大于內側輪的側向力；單個四點式起落架飛機前輪比三點式起落架飛機前輪的側向力小得多；與圖5相比，在仿真時間內，所有前輪的側向力均比較小，是由于剎車力矩引起單邊主輪航向摩擦力增大，而飛機差動剎車轉彎主要是由該摩擦力對飛機產生偏航力矩。

差動剎車主輪側向力如圖8所示。

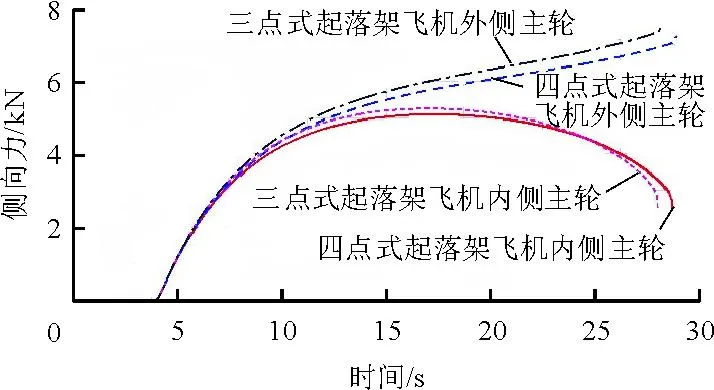
圖8　差動剎車主輪側向力

從圖8可以看出：在差動剎車過程中，無論起落架布局如何，外側主輪的側向力總大于內側主輪；兩種布局飛機的內外主輪的側向力大致相當，而完成的轉彎半徑也大致相同(如圖6所示)。

3.3四點式起落架飛機不同前輪作主動輪時轉彎半徑分析

四點式起落架飛機在不同轉彎驅動策略下，轉彎效率明顯不同。在給定飛機滑行速度為30 km/h，前起落架分別在雙輪驅動、外側輪驅動和內側輪驅動的條件下，機輪轉角為10°時，探討飛機的轉彎半徑。不同輪作主動輪飛機的轉彎半徑如圖9所示。

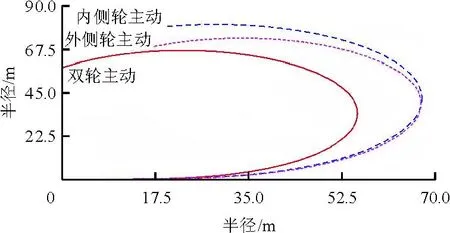
圖9　不同輪作主動輪飛機的轉彎半徑

從圖9可以看出：當四點式起落架飛機雙輪均為主動輪時，飛機的轉彎半徑最小；外側輪為主動輪時，轉彎半徑次之；內側輪為主動輪時，轉彎半徑最大。

飛機在單輪主動操縱轉彎時，隨動輪處于減擺狀態，只產生很小的側向力，對飛機轉彎效率影響較小，如圖10～圖11所示。

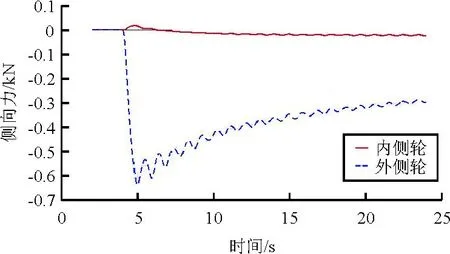
圖10　外側輪作主動輪的側向力

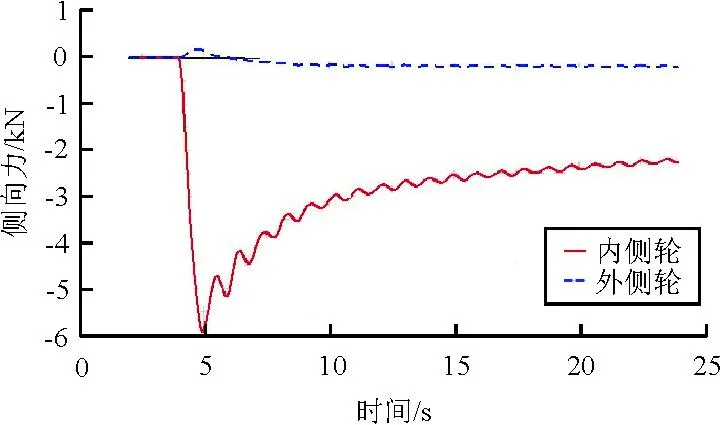
圖11　內側輪作主動輪的側向力

不同輪作主動輪時的輪胎側向力如表1所示。

表1　不同輪作主動輪時的輪胎側向力

從圖5和表1可以看出：在雙輪主動時，內側輪比外側輪的側向力小；而單輪主動時，內側輪主動的內側輪側向力比外側輪主動的外側輪側向力小。

4結論

(1) 不同起落架布局飛機前輪操縱時，在相同的滑跑條件下，四點式起落架飛機比三點式起落架飛機轉彎半徑更小，擁有較高的轉彎效率；四點式起落架飛機單個前起所承受的側向力比三點式起落架飛機前起的側向力小。

(2) 不同起落架布局飛機主輪差動剎車時，在相同的滑跑條件下，四點式起落架飛機轉彎半徑略大于三點式起落架飛機。由于偏航力矩主要是由單邊主輪的摩擦力提供，前起落架的側向力較小，但單個前起落架側向力比三點式起落架飛機的前起落架小。

(3) 四點式起落架飛機在相同的滑跑條件下，雙輪均為主動輪時，飛機的轉彎半徑最小，轉彎效率最高；外側輪為主動輪時，轉彎效率次之；內側輪為主動輪時的轉彎半徑最大，轉彎效率最低；轉彎過程中外側輪的側向力大于內側輪的側向力。

參考文獻

[1] Pollack H M, Urch R E. Landing gear design requirements for bomb-damaged runway operations[R]. SAE Technical Paper, 1991.

[2] Goldthorpe S H, Dangaran R D, Dwyer J P, et al. Guidance and control design for high-speed rollout and turnoff(ROTO)[R]. NASA-CR-201602, 1996.

[3] Barnes A G, Yager T J. Enhancement of aircraft ground handling simulation capability[R]. AGARD-AG-333, 2000.

[4] 顧宏斌. 飛機地面運行的動力學模型[J]. 航空學報, 2001, 22(2): 163-167.

Gu Hongbin. Dynamic model of aircraft ground handling[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(2): 163-167.(in Chinese)

[5] 朱天文. 飛機地面操縱轉彎半徑和轉彎速度計算方法研究[J]. 飛機設計, 2003(3): 31-34.

Zhu Tianwen. Study on calculative method of aircraft steering turning radius and turning velocity[J]. Aircraft Design, 2003(3): 31-34.(in Chinese)

[6] 金秀芬, 李凱, 于秀偉. 民用飛機地面轉彎時重心側向過載系數的分析與研究[J]. 航空工程進展, 2012, 3(3): 317-321.

Jin Xiufen, Li Kai, Yu Xiuwei. Research of side load factor for civil aircraft ground turning[J]. Advances in Aeronautical Science and Engineering, 2012, 3(3): 317-321.(in Chinese)

[7] 錢小妹. 飛機操縱前輪轉彎特性仿真研究[D]. 南京： 南京航空航天大學, 2008.

Qian Xiaomei. Research on steering nose wheel of aircraft by dynamic simulation[D]. Nanjing： Nanjing University of Aeronautics and Astronautics, 2008.(in Chinese)

[8] 王孝英, 諸德培. 飛機操縱前輪轉彎運動的數學模型及數值仿真[J]. 應用力學學報, 1997, 14(4): 46-50.

Wang Xiaoying, Zhu Depei. A mathematical model and digital simulation of aircraft turn by steering nose wheel[J]. Chinese Journal of Applied Mechanics, 1997, 14(4): 46-50.(in Chinese)

[9] 孫澤鵬, 聶宏, 鄭藍. 飛機地面操縱動態特性和方向穩定性研究[J]. 機械工程師, 2008(11): 58-60.

Sun Zepeng, Nie Hong, Zheng Lan. Research on aircraft ground handling dynamic characters and direction stability[J]. Mechanical Engineer, 2008(11): 58-60.(in Chinese)

[10] 常正, 聶宏, 馮飛, 等. 飛機柔性前起落架擺振仿真分析[J]. 航空工程進展, 2011, 2(4): 432-436.

Chang Zheng, Nie Hong, Feng Fei, et al. Shimmy simulation analysis of aireraft flexible nose landing gear[J]. 2011, 2(4): 432-436.(in Chinese)

[11] 羅東, 龔華軍, 袁鎖中, 等. 起落架四點布局無人機地面運動研究[J]. 飛行力學, 2008, 26(1): 24-27.

Luo Dong, Gong Huajun, Yuan Suozhong, et al. Ground motion studying of an UAV with four wheels[J]. Flight Dynamics, 2008, 26(1): 24-27.(in Chinese)

[12] Masato Abe. 車輛操縱動力學[M]. 喻凡, 譯. 北京: 機械工業出版社, 2006: 68-93.

Masato Abe. Vehicle handling dynamics[M]. Translated by Yu Fan. Beijing: Machinery Industry Press, 2006: 68-93.(in Chinese)

[13] 張明. 飛機地面動力學若干關鍵技術研究[D]. 南京: 南京航空航天大學, 2009.

Zhang Ming. Research on some key technologies of aircraft ground dynamics[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.(in Chinese)

茍能亮(1990-)，男，碩士研究生。主要研究方向：起落架設計與分析。

苑強波(1973-)，男，高級工程師。主要研究方向：起落架設計。

張明(1981-)，男，博士，副教授。主要研究方向：起落裝置設計、飛行器系統動力學。

(編輯：趙毓梅)

Analysis of Aircraft Landing Gear with Four Wheels Ground Taxiing Turning

Gou Nengliang1， Yuan Qiangbo2， Zhang Ming1

(1.Key Laboratory of Fundamental Science for National Defense-advanced Design Technology of Flight Vehicle， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China)(2.Department of Structure Design， Shenyang Aircraft Design & Research Institute， Shenyang 110035， China)

Abstract:Ground taxiing turning performances of modern aircraft are required to be increasingly improved, and are demanded to work in the more harsh circumstance than before. The research object is based on an aircraft with four wheels. The relationship of angle between two nose landing gear wheels is calculated based on the geometrical principle of Ackerman steering during taxiing procedure. Four wheels aircraft simulated prototype is built and four wheels aircraft ground taxiing simulation has been conducted as well. The influence on turning radius of the four wheels aircraft is investigated when using respective nose wheels as driving wheels. Result shows that four wheels aircraft turning radius is smaller than conventional three wheels aircraft under the same taxiing circumstances when nose wheel steering is applied. Four wheels aircraft turning radius is slightly more than three wheels aircraft when main wheel is differential braking. When both nose wheels steering are applied, the four wheels aircraft has minimum turning radius.

Key words:landing gear with four wheels; nose wheel steering; differential braking; turning radius

作者簡介：

中圖分類號：V226

文獻標識碼：A

DOI：10.16615/j.cnki.1674-8190.2016.01.003

文章編號:1674-8190(2016)01-017-07

通信作者：張明,zhm6196@nuaa.edu.cn

收稿日期：2015-10-19；修回日期：2015-11-02