微型撲翼仿生“0”字和“8”字形撲動方式氣動特性研究

張紅梅，楊文青

(西北工業(yè)大學 航空學院，西安　710072)

?

微型撲翼仿生“0”字和“8”字形撲動方式氣動特性研究

張紅梅，楊文青

(西北工業(yè)大學 航空學院，西安710072)

摘要：微型撲翼飛行器的氣動特性由撲翼的運動規(guī)律所決定，為了研究復雜翼梢軌跡對撲翼氣動特性的影響，通過對上下?lián)鋭印⑾蚁蚺まD和前后掠動三個自由度的運動設計不同的參數(shù)，運用數(shù)值模擬方法研究微型撲翼采用仿生“0”字形和“8”字形運動時的氣動特性。結果表明：相比于傳統(tǒng)的撲動運動，增加了掃掠運動的“0”字形和“8”字形撲動可有效增加升力，特別是“8”字形撲動的增升效果更加顯著，但同時也會造成阻力略增，可以通過調(diào)整扭轉角度來增加推力。本文的研究結果可為復雜運動規(guī)律下微型撲翼飛行器設計提供參考。

關鍵詞：氣動特性；微型撲翼；仿生撲動；數(shù)值模擬

0引言

飛鳥、飛行昆蟲、蝙蝠等自然界的飛行生物均采用撲翼方式飛行，尺度縮小后，撲翼飛行是一種可有效提高氣動性能的飛行方式。微型撲翼飛行器(Flapping-wing Micro Air Vehicle，簡稱FMAV)是一種仿生飛行器，但是目前人造的微型撲翼飛行器和飛行生物的飛行能力相比，還相差甚遠。

近年來，F(xiàn)MAV受到廣泛關注，包括美國、歐盟、日本以及中國在內(nèi)的世界各國競相對其展開研究，同時，也得到了諸多研究成果，涉及氣動計算、風洞實驗等多個方面，揭示了FMAV氣動特性的產(chǎn)生機理。K.Viswanath等[1]研究發(fā)現(xiàn)下?lián)溥^程中若遭遇前向突風，會使升力和推力同時增加；P.Wu等[2]的研究表明某些變形模式可以使推力增加；D.D.J.Chandar等[3]研究發(fā)現(xiàn)推力是由對稱渦街產(chǎn)生的；S.K.Chimakurth等[4]研究得出展向變形和前緣吸力均有利于增加推力的結論；S.A.Ansari等[5-6]認為較直的前緣有利于升力特性；Y.S.Hong等[7-8]研究表明翼尖渦和展向彎度會對升力產(chǎn)生顯著影響。上述研究主要關注了FMAV在撲翼上下?lián)鋭忧闆r下的氣動特性，目前已有少量文獻研究了在撲動運動中增加掠動角度對氣動特性的影響。例如，J.A.Esfahani等[9]研究了二維翼型存在掠動運動情況下的氣動特性；K.Viswanath等[10]研究了仿昆蟲尺度的薄翼型在復雜運動情況下的氣動特性，得到了運動與氣動特性的對應關系。

微型撲翼飛行器的氣動特性完全由撲翼的運動規(guī)律決定，自然界飛行生物為微型撲翼飛行器的設計提供了寶貴的借鑒，仿生研究是提高FMAV撲翼飛行能力的一個重要途徑。自然界飛行生物的翼稍軌跡并非簡單的往復撲動，而是帶有一些掠動，使得翼稍軌跡形成不同的曲線。飛行生物的翼稍軌跡如圖1所示[11]，常見的有“0”字形和“8”字形。

圖1　不同飛行生物的翼稍運動軌跡

本文針對包含前后掃掠的撲動運動的氣動特性展開研究，考慮到現(xiàn)有技術條件下仿鳥尺度飛行器具有更強的可實現(xiàn)性，選擇仿鳥尺度的微型撲翼為研究對象，通過對其三個自由度的運動設計不同的參數(shù)，研究三維撲翼采用仿生“0”字形和“8”字形(為了研究方便，假設理想的“0”字形和“8”字形規(guī)律)運動時的氣動特性。

1撲動方式定義

按照轉軸的不同，撲翼的運動可分為：上下?lián)鋭印⑾蚁蚺まD和前后掠動(以下簡稱撲動、扭轉和掠動)，如圖2所示，其中，撲動運動為繞x軸的轉動，扭轉運動為繞z軸的轉動，掠動運動為繞y軸的轉動。撲動與扭轉被認為是基本運動方式，當加入不同的掠動頻率后，撲翼翼稍軌跡將體現(xiàn)出不同的形態(tài)，本節(jié)將分別定義。

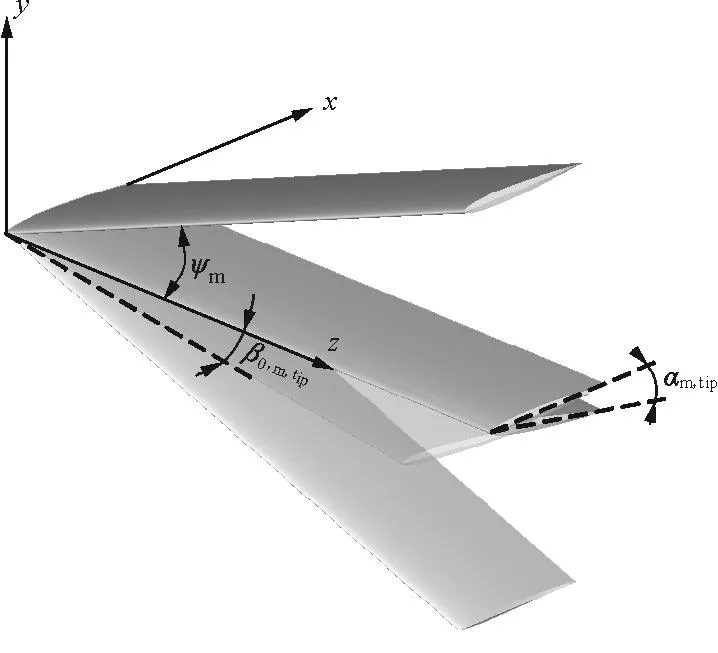
圖2　撲翼運動示意圖

1.1基本運動

基本運動包括撲動和扭轉。撲動運動規(guī)律為

ψ(t)=ψmcos(ωt)

(1)

扭轉運動規(guī)律為

α(z,t)=α0-αm(z)sin(ωt)

(2)

(3)

式中：ψ為在t時間步的撲動幅度；ψm為最大撲動幅度；ω為撲動頻率；α為在t時間步的瞬時迎角，也稱之為扭轉角(包含扭轉變形導致的迎角變化)；α0為初始迎角；αm為最大扭轉角；z為展向站位；b為半展長。

撲翼按照基本運動規(guī)律的運動如圖3所示，扭轉與撲動的相位差為90°，該相位差下推進效率最高[12-14]。

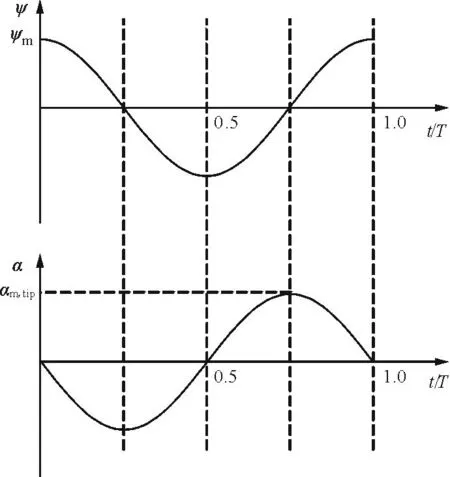
(a) 撲動和扭轉的角度函數(shù)

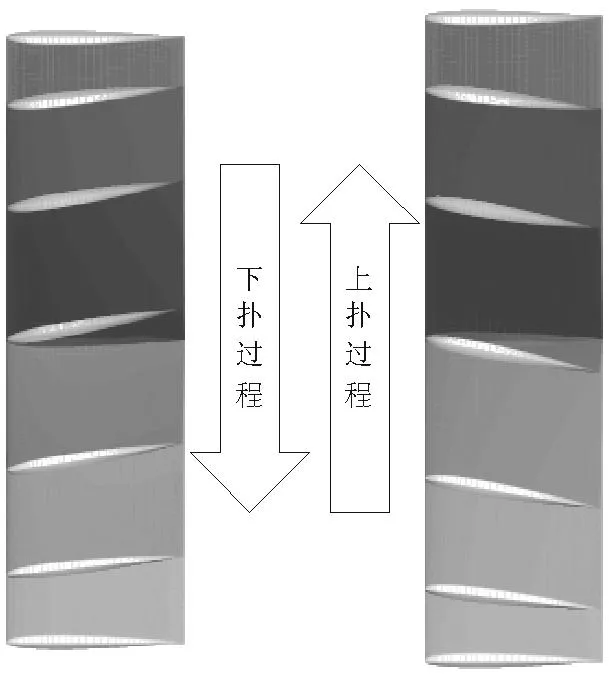
(b) 撲動和扭轉的運動規(guī)律

1.2“0”字形與“8”字形撲動

在基本運動規(guī)律上，增加一定的掠動規(guī)律，即可形成“0”字形或者“8”字形運動規(guī)律，這兩種規(guī)律的區(qū)別在于掠動的頻率不同。若掠動頻率等于撲動頻率，則翼尖軌跡體現(xiàn)為“0”字形；若掠動頻率為撲動頻率的兩倍，則翼尖軌跡體現(xiàn)為“8”字形。當掠動頻率更高時，翼尖軌跡則更為復雜，該撲動方式也比較少見，不具有代表性，本文不討論其影響與規(guī)律。

“0”字形撲動運動情況下，掠動角度的變化規(guī)律為

β0(z,t)=β0,m(z)sin(ωt)

(4)

(5)

“8”字形撲動運動情況下，掠動角度的變化規(guī)律為

β8(z,t)=β8,m(z)sin(2ωt)

(6)

(7)

式中：β*(*為“0”或“8”)為“0”字形或“8”字形運動規(guī)律下，t時刻在展向站位z的瞬時掠動角度；β*,m為“0”字形或“8”字形運動規(guī)律下，在展向站位z的最大掠動角度；β*,m,tip為“0”字形或“8”字形運動規(guī)律下，翼稍最大掠動角度。

“0”字形掠動規(guī)律與翼運動示意圖如圖4所示。

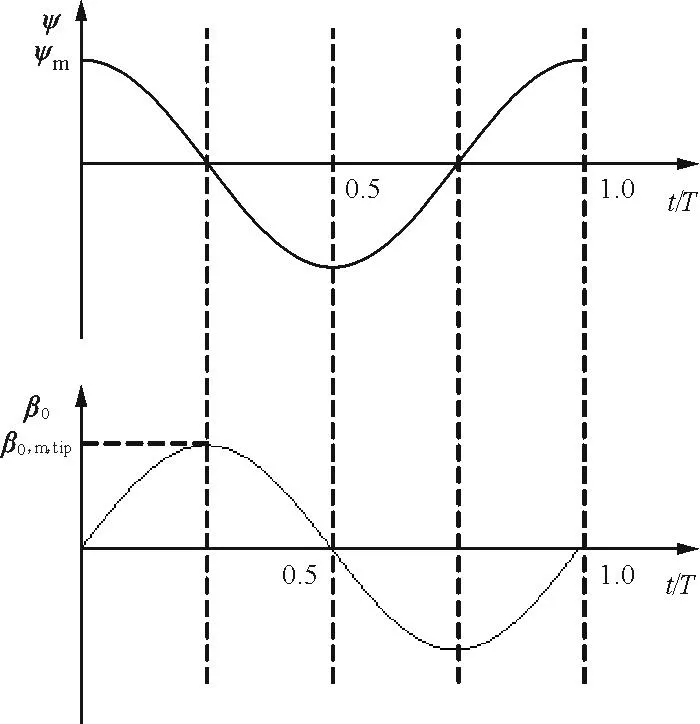
(a) “0”字形掠動的角度函數(shù)

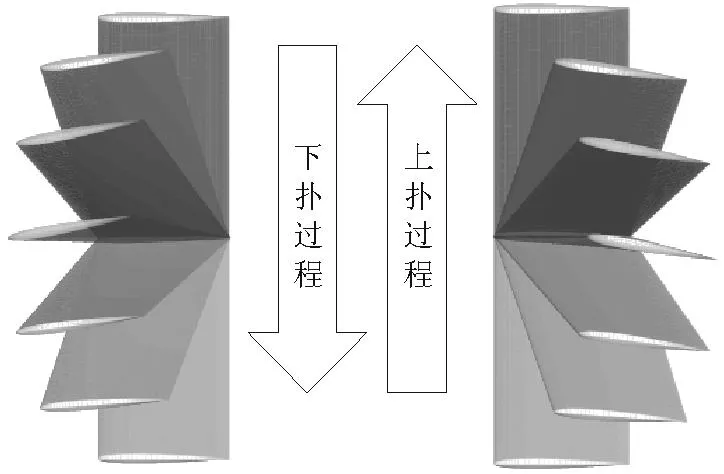
(b) “0”字形掠動的運動規(guī)律

“8”字形掠動規(guī)律與翼運動示意圖如圖5所示。

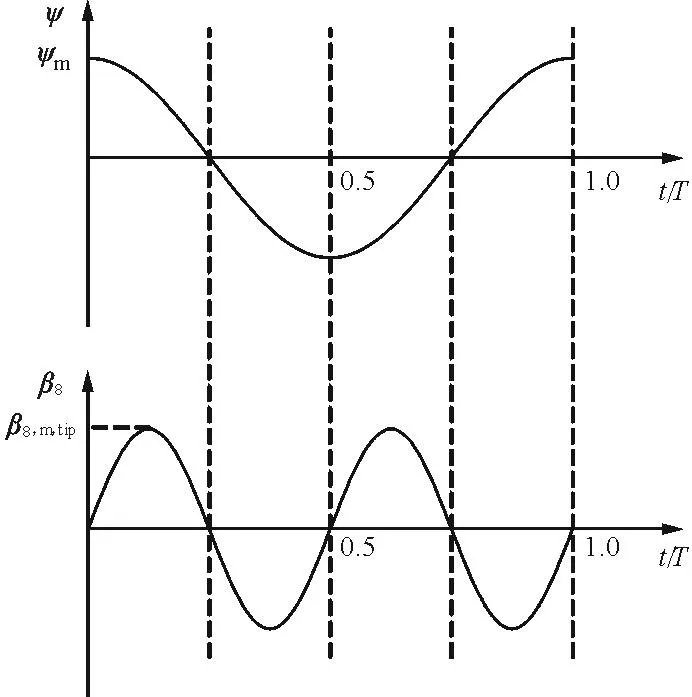
(a) “8”字形掠動的角度函數(shù)

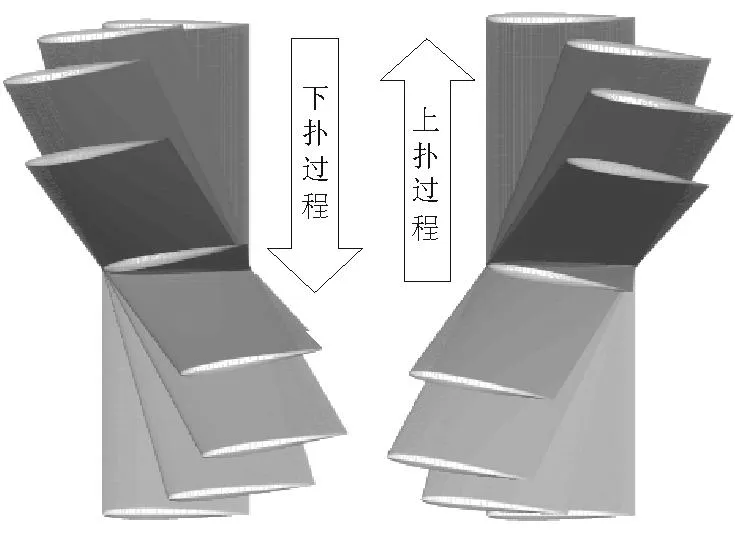
(b) “8”字形掠動的運動規(guī)律

2數(shù)值方法

采用數(shù)值模擬方法研究微型撲翼仿生復雜撲動情況下的氣動特性。微型撲翼飛行器速度低、尺度小，其繞流具有低馬赫數(shù)、低雷諾數(shù)的特點，受空氣粘性的影響很大，故采用雷諾平均N-S(Reynolds-Averaged Navier-Stokes，簡稱RANS)方程作為基本控制方程[15]。

在連續(xù)介質(zhì)假設下，忽略徹體力和熱源的三維非定常可壓縮RANS方程可寫為如下守恒形式

(8)

其中，

W=[ρ,ρu,ρv,ρw,ρE]T

E=[ρu,ρu2+p,ρuv,ρuw,(ρE+p)u]T

F=[ρv,ρuv,ρv2+p,ρvw,(ρE+p)v]T

G=[ρw,ρwu,ρwv,ρw2+p,(ρE+p)w]T

Ev=[0,τxx,τxy,τxz,βx]T

Fv=[0,τyx,τyy,τyz,βy]T

Gv=[0,τzx,τzy,τzz,βz]T

式中：ρ、(u,v,w)、p、E分別為流體的密度、速度在直角坐標系下的三個分量、壓力、單位質(zhì)量總能。

單位質(zhì)量總能(E)和單位質(zhì)量總焓(H)分別為

(9)

H=E+p/ρ

(10)

完全氣體的壓力和溫度狀態(tài)方程為

p=ρ(γ-1)e

(11)

T=p/(Rρ)

(12)

式中：e為單位質(zhì)量內(nèi)能；γ為比熱比，對于空氣取1.4；R為氣體常數(shù)。

采用中心格式有限體積法求解積分形式的N-S方程，認為守恒流動變量在網(wǎng)格單元中心，時間推進方法采用顯式Runge-Kutta混合多步法和隱式LU-SGS方法，非定常計算采用雙時間法。采用預處理方法求解低馬赫數(shù)下的收斂問題。湍流模型采用SSTk -ω二方程模型。

撲翼計算網(wǎng)格基于嵌套網(wǎng)格方法，該方法不要求各子域共享邊界，可有效減輕各區(qū)自身網(wǎng)格生成的難度，避免了計算網(wǎng)格扭曲過大、網(wǎng)格疏密分布不合理的狀況，非常適合復雜外形或者有相對運動的情況。各個重疊子域的流場解在內(nèi)邊界要求必須光滑，通常由插值來實現(xiàn)，從而得到整個流場的解。洞點識別和插值單元尋址是重疊網(wǎng)格的兩個關鍵技術。本文采用“距離減縮法”[16]高效確定不同網(wǎng)格之間的對應單元，進而快速進行洞點識別，該方法效率高、易于實現(xiàn)，應用于插值單元尋址時，能夠快速鎖定插值貢獻單元。本文所用的數(shù)值方法，已經(jīng)過驗證，其過程詳見文獻[16]。

計算網(wǎng)格如圖6所示。

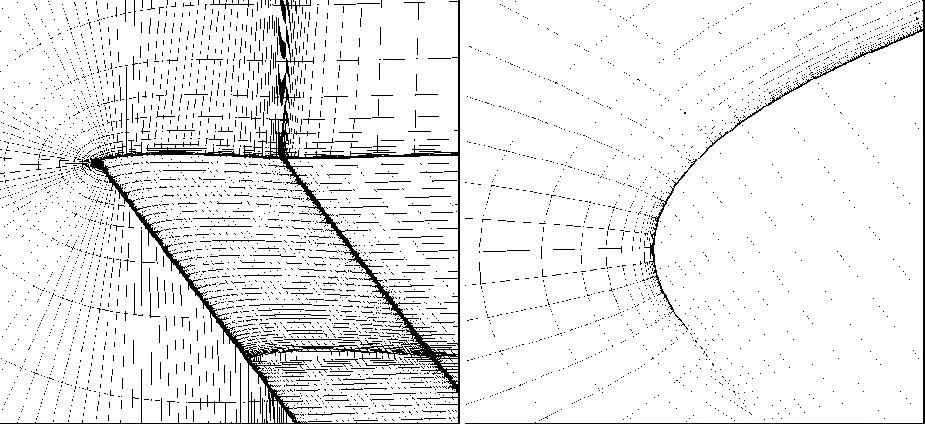
圖6　撲翼計算使用的網(wǎng)格

3結果分析

作為基本規(guī)律研究，采用半展弦比為4的直機翼，翼型為NACA0008。考慮到仿鳥的研究范疇，取馬赫數(shù)(Ma)為0.03，雷諾數(shù)(Re)為7×104，迎角(α0)為5°，撲動幅度(ψm)為20°，減縮頻率(k)為0.2，其余參數(shù)詳見各小節(jié)。

3.1升力和阻力特性

(1) 計算無掠動情況下的氣動特性，扭轉角變化范圍為0°～25°，間隔3°。扭轉角變化對升力系數(shù)和阻力系數(shù)的影響如圖7所示。

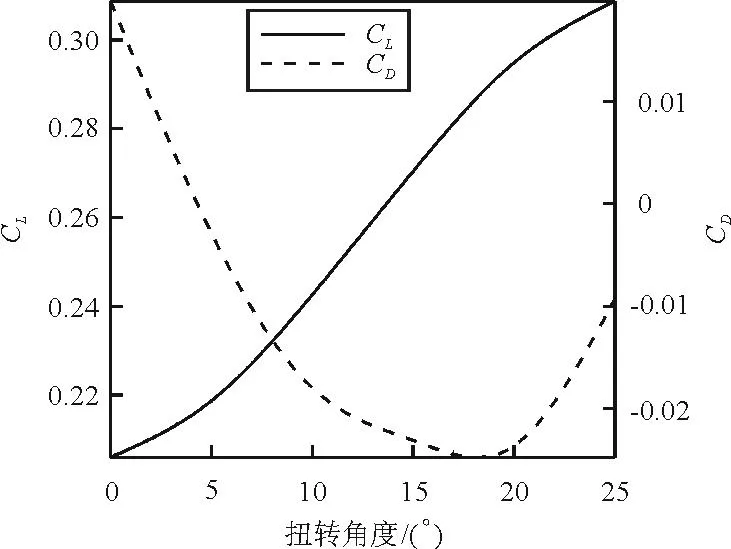
圖7　扭轉角對升力和阻力的影響規(guī)律

從圖7可以看出：當扭轉角在18°范圍內(nèi)時，隨著扭轉角的增大，升力系數(shù)和推力系數(shù)均增加(即阻力系數(shù)減小，因為推力系數(shù)和阻力系數(shù)為相反數(shù))；當扭轉角大于18°時，推力減小。18°是個較大的數(shù)值，實際中的扭轉角通常不會超過18°，因此，增加撲動時的扭轉角可有效增加升力和推力，通過增加扭轉角可改變飛行狀態(tài)，例如改變飛行速度或高度等。

(2) 計算“0”字形撲動運動方式下的氣動特性。掠動角度變化范圍為0°～20°，間隔2°。“0”字形撲動方式下掠動角度對升力和阻力特性的影響規(guī)律如圖8所示，可以看出：當掠動角度很小時(小于4°)，增加掠動角會減小升力，但卻增加推力；當掠動角度在中等范圍時(4°～6°)，增加掠動角會使升力和推力同時增大；當掠動角度繼續(xù)增加時(大于6°)，增加掠動角度會增加升力，但卻減小推力。

圖8　“0”字形撲動時掠動角對升力和阻力的影響規(guī)律

在“0”字形撲動規(guī)律下，掠動角度對氣動特性變化規(guī)律的影響比較復雜，小范圍掠動角的增加對推力有利，而大范圍掠動角的增加對升力有利。

(3) 計算“8”字形撲動運動方式下的氣動特性。掠動角度變化范圍為0°～20°，間隔2°。“8”字形撲動方式下掠動角度對升力和阻力特性的影響規(guī)律如圖9所示。

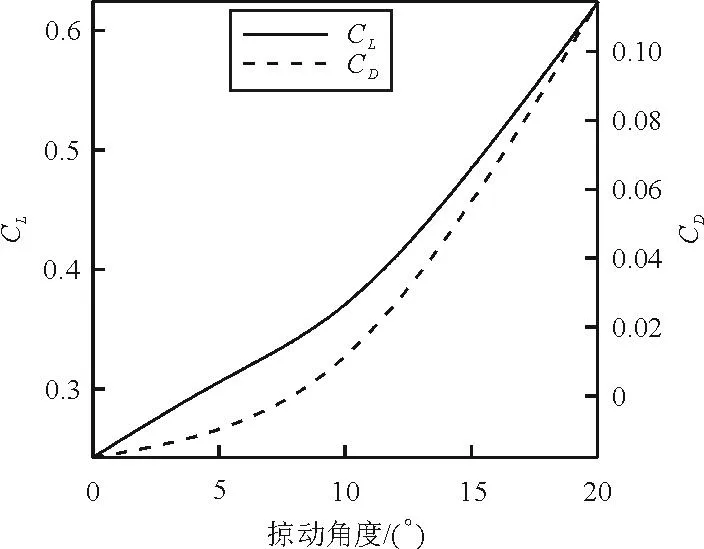
圖9　“8”字形撲動時掠動角對升力和阻力的影響規(guī)律

從圖9可以看出：“8”字形撲動規(guī)律下，隨著掠動角的增加，升力增加但推力減小；當掠動角度在較小范圍變化時(小于7°)，升力的增加比例大于推力的減小比例；當掠動角度在較大范圍變化時(大于7°)，升力的增加比例小于推力的減小比例。

“8”字形撲動方式對升力有利，但卻以降低推力為代價。

3.2流場分析

展向50%截面處的流場壓力云圖，如表1所示。

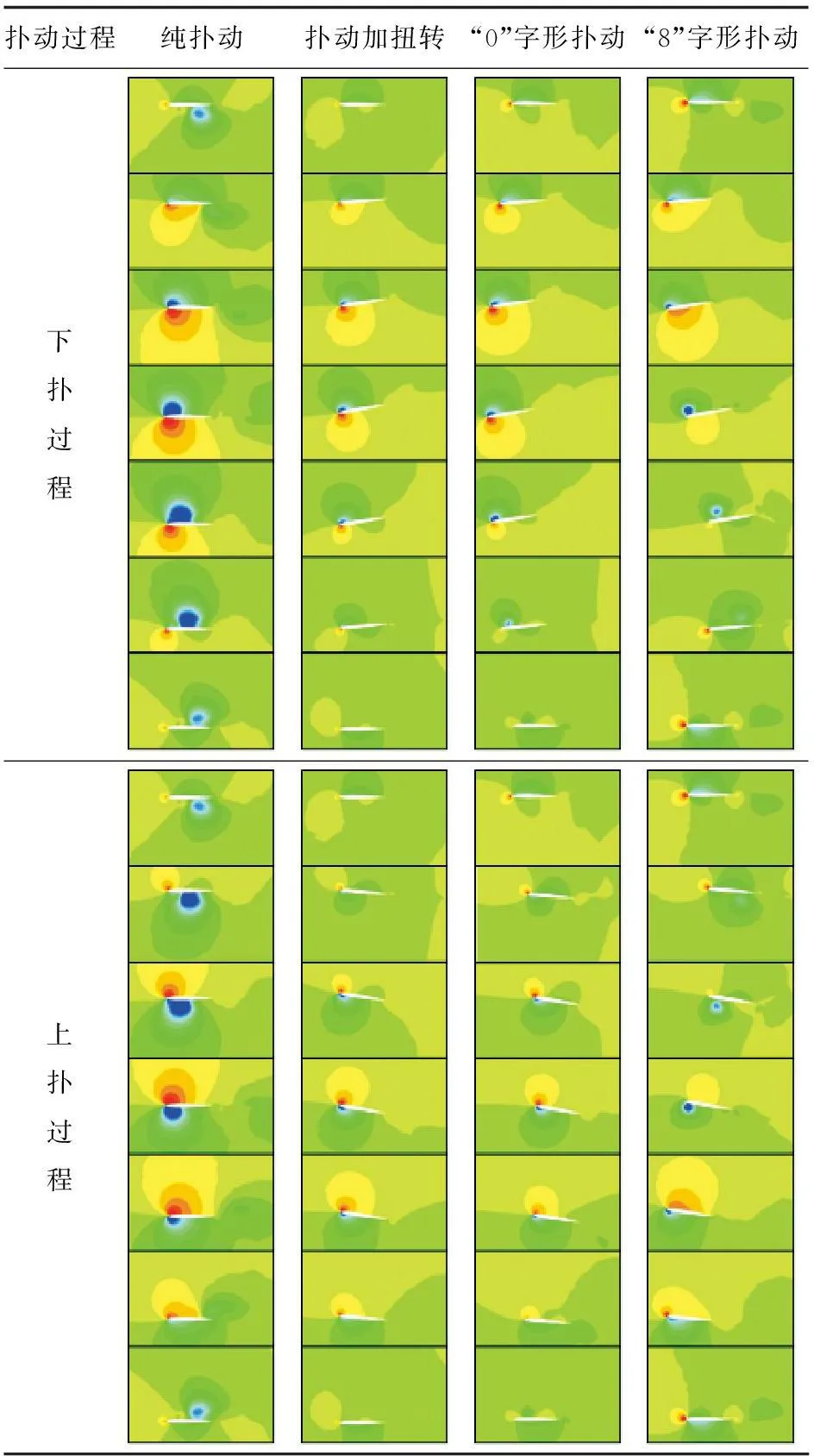
表1　不同撲動方式流場壓力變化云圖

從表1可以看出:“純撲動”產(chǎn)生的壓力波動范圍最大，表明“純撲動”產(chǎn)生的氣動力波動范圍也最大；在“純撲動”過程中，有相當一部分氣動力在上撲和下?lián)涞倪^程中被抵消，造成運動的浪費；“撲動加扭轉”的壓力波動情況優(yōu)于“純撲動”，其壓力變化范圍減小，且后緣壓力增大，有利于增加推力；“0”字形撲動方式在下?lián)溥^程中，由于有向前的掠動，增強了升力，但同時也增加了阻力；“8”字形撲動方式由于掠動時速度更快，對升力有較強的增加作用，但同時也顯著增加了阻力。

4結論

(1) “純撲動”的效果很差，“撲動加扭轉”的運動方式對升力和推力均有益處，增加掠動運動后主要增加升力，“8”字形撲動方式比“0”字形撲動方式在增強升力方面效果更好。

(2) 從運動機理上講，掠動運動其本質(zhì)是在一定程度上改變了撲翼的合速度方向，從而影響了有效攻角，導致不同的氣動特性。

(3) 增加撲動時的扭轉角可有效增加升力和推力，從而改變飛行狀態(tài)；通過利用掠動角也可達到增升的目的。

(4) 本文的研究結果可為復雜運動規(guī)律的微型撲翼飛行器設計提供了參考。

參考文獻

[1]ViswanathK,TaftiDK.Effectoffrontalgustsonforwardflappingflight[J].AIAAJournal, 2010, 48(9): 2049-2062.

[2]WuP,IfjuP,StanfordB.Flappingwingstructuraldeformationandthrustcorrelationstudywithflexiblemembranewings[J].AIAAJournal, 2012, 48(9): 2111-2122.

[3]ChandarDDJ,DamodaranM.Computationofunsteadylowreynoldsnumberfree-flightaerodynamicsofflappingwings[J].JournalofAircraft, 2010, 47(1): 141-150.

[4]ChimakurthSK,TangJ,PalaciosR,etal.Computationalaeroelasticityframeworkforanalyzingflappingwingmicroairvehicles[J].AIAAJournal, 2009, 47(8): 1865-1878.

[5]AnsariSA,KnowlesK,ZbikowskiR.InsectlikeflappingwingsinthehoverpartⅠ:effectofwingkinematics[J].JournalofAircraft, 2008, 45(6): 1945-1954.

[6]AnsariSA,KnowlesK,ZbikowskiR.InsectlikeflappingwingsinthehoverpartⅡ:effectofwinggeometry[J].JournalofAircraft, 2008, 45(6): 1976-1990.

[7]HongYS,AltmanA.Streamwisevorticityinsimplemechanicalflappingwings[J].JournalofAircraft, 2007, 44(5): 1588-1597.

[8]HongYS,AltmanA.Liftfromspanwiseflowinsimpleflappingwings[J].JournalofAircraft, 2008, 45(4): 1206-1216.

[9]EsfahaniJA,BaratiE,KarbasianHR.Fluidstructuresofflappingairfoilwithellipticalmotiontrajectory[J].Computers&Fluids, 2014, 108: 142-155.

[10]ViswanathK,TaftiDK.Effectofstrokedeviationonforwardflappingflight[J].AIAAJournal, 2013, 51(1): 145-160.

[11]ShyyW,LianY,TangJ,etal.AerodynamicsoflowReynoldsnumberflyers[M].UK:CambridgeUniversityPress, 2008.

[12]JonesKD,PlatzerMF.Numericalcomputationofflapping-wingpropulsionandpowerextraction[C].AIAA-97-0826, 1997.

[13]TuncerIH,WalzR,PlatzerMF.Acomputationalstudyonthedynamicstallofaflappingairfoil[C].AIAA-98-2519, 1998.

[14]IsogaiK,ShinmotoY,WatanabeY.Effectsofdynamicstallonpropulsiveefficiencyandthrustofflappingairfoil[C].AIAA-97-1926, 1997.

[15] 韓忠華, 喬志德, 熊俊濤, 等.Navier-Stokes方程預處理方法及其對翼型繞流數(shù)值模擬的應用[J]. 西北工業(yè)大學學報, 2006, 24(3): 275-280.

HanZhonghua,QiaoZhide,XiongJuntao,etal.Developmentofanefficientviscouspreconditioningmethodanditsapplicationtonumericalsimulationofflowsoverairfoils[J].JournalofNorthwesternPolytechnicalUniversity, 2006, 24(3): 275-280.(inChinese)

[16] 楊文青, 宋筆鋒, 宋文萍. 高效確定重疊網(wǎng)格對應關系的距離減縮法及其應用[J]. 航空學報, 2009, 30(2): 205-212.

YangWenqing,SongBifeng,SongWenping.Distancedecreasingmethodforconfirmingcorrespondingcellsofoversetgridsanditsapplication[J].ActaAeronauticaetAstronauticaSinica, 2009,30(2): 205-212.(inChinese)

張紅梅(1969-)，女，助理工程師。主要研究方向：微型飛行器。

楊文青(1980-)，女，博士，副教授。主要研究方向：微型飛行器、非定常氣動特性。

(編輯：馬文靜)

Investigation of “0”-Figure and “8”-Figures Wingtip Path Effect on Aerodynamic Performance of Micro Flapping-wing

Zhang Hongmei, Yang Wenqing

(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:The aerodynamic performance of flapping-wing micro air vehicle(FMAV) is determined completely by the motion of flapping wings. In order to study the complex wingtip trajectory influence on the aerodynamic characteristics, the “0” and “8” figures effects are investigated by numerical method. The movement is divided into three degrees of freedom: plunging, pitching and swing with different parameters setting. The numerical results show that, compared with the traditional flapping motion, the flapping manners in “0” and “8” figures can effectively increase the lift because of the added swing motion, especially in the “8” figure flapping. However, the drag increased slightly at the same time. The thrust can be increased by adjusting the pitching angle. This study can be provided as a reference for the FMAV design with a complex wingtip trajectory.

Key words:aerodynamic performance; micro flapping-wing; bionic flapping; numerical simulation

作者簡介：

中圖分類號：V211.3

文獻標識碼：A

DOI：10.16615/j.cnki.1674-8190.2016.01.007

文章編號:1674-8190(2016)01-044-07

通信作者：張紅梅,zhm@nwpu.edu.cn

基金項目：國家自然科學基金(11402208)

收稿日期：2015-10-27；修回日期：2016-01-05

中央高校基本科研業(yè)務費專項資金(310201401JCQ01002)