基于AHP-熵權法的地下水水質模糊綜合評價
----以白城市為例

郝 洋，梁秀娟，孟凡傲，肖長來，王百陽

(1.吉林大學 地下水資源與環境教育部重點實驗室，長春 130021；2.吉林大學 環境與資源學院，長春 130021)

地下水水質評價是地下水資源評價的一項重要組成部分，水質的優劣影響著當地居民的生活質量、經濟發展以及社會建設，地下水水質評價是地下水資源合理開發利用的基礎和依據。目前，地下水水質評價方法較多，主要有內梅羅綜合指數法、物元可拓法、灰色聚類法、人工神經網絡法、模糊綜合評價法等[1]。其中，模糊綜合評價法引入隸屬度這一概念，區域內地下水水質的分布變化是漸變的過程，具有界線模糊的特點，模糊綜合評價法在處理這類模糊性問題時效果比較理想，因而在地下水水質評價中應用較為廣泛[2]。Zhou等人運用模糊數學法對山東省地下水水質進行評價[3]；Han運用模糊綜合評價法對沈陽化學工業園進行風險性評價[4]。然而，傳統的模糊綜合評價法的權重確定一般采用污染物濃度超標加權法，過度強調了地下水中主要超標組分對地下水水質的影響。盧文喜等人對模糊綜合評價法進行了改進[5]。鑒此，為使評價結果更為準確、合理，本文在權重的確定上采用AHP和熵權法相結合的賦權方法，將專家的經驗知識和各個數據的信息充分結合，另外，考慮到傳統的模糊綜合評價法的最大隸屬度原則具有條件性和不安全性[6]，為使評價結果更加準確，本文將用級別特征值來代替最大隸屬度原則。

1 研究區概況

白城市位于吉林省西北部，嫩江平原西部，吉林、黑龍江和內蒙古自治區三省交界處。白城市下轄洮北區、洮南市、鎮賚縣、通榆縣、大安市等五個區縣。東南與吉林省松原市接壤，西北與內蒙古自治區相連，東北與黑龍江省隔江相望。白城市地處大興安嶺山脈東麓平原區，氣候屬溫帶大陸性季風氣候，年平均降水量為400 mm[7]。

本文以白城市2013年各區縣的20個監測井地下水水質監測資料為數據，其中洮北區、洮南市、鎮賚縣、通榆縣、大安市各4口監測井(圖1)。并根據當地水質情況選取了氟化物、總鐵、亞硝酸鹽氮、錳、總硬度、氯化物、硫酸鹽、硝酸鹽氮、氨氮共9個指標作為評價指標。

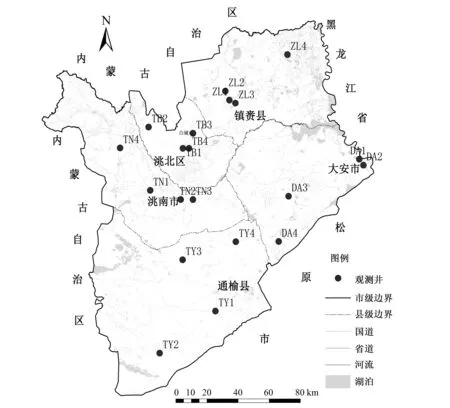
圖1 研究區測井分布圖Fig.1 The distribution of wells in study area

2 基于AHP-熵權法的模糊綜合評價法

2.1 建立因子集和評價集

由n個影響水質的因素組成的評價因素集合為：

U={u1,u2,…,un}

由m個評價等級組成的評價等級集合為：

V={v1,v2,…,vm}

2.2 建立模糊關系矩陣

隸屬度函數是模糊綜合評價的基礎，一般采用降半梯形分布法計算隸屬度函數，確定各指標屬于各水質級別的隸屬度函數。各級水質隸屬度函數如下：

Ⅰ級水質(j=1)的隸屬度函數為：

(1)

Ⅱ-Ⅳ級水質(j=2，3，4)的隸屬度函數為：

(2)

Ⅴ級水質(j=5)的隸屬度函數為：

(3)

由以上建立的隸屬度函數可以確定一個i×5的模糊關系評價矩陣R，即：

(4)

式中：xi為第i種評價指標的實測濃度；sij為第i種評價指標的j級水質標準值；rij為第i種評價指標對j級水質的隸屬度。

2.3 確定評價指標的權重

評價指標權重的確定直接影響地下水水質評價的準確性，傳統的模糊綜合評價法的權重確定一般采用污染物濃度超標加權法，過度突出地下水中主要超標組分對地下水水質的影響，因此，本文采用AHP-熵權法來確定各個評價的權重，運用這種主客觀相結合的綜合賦權法，將使地下水水質評價更加合理。

2.3.1AHP法

AHP法又稱層次分析法，是美國匹茲堡大學教授沙提(T.L.Saaty)在20 世紀70 年代提出的[7]。采用九級標度法對各個評價指標進行兩兩比較，確定其相對重要性(表1)，然后建立數學模型，計算各指標相對重要性權值，并進行一致性檢驗。

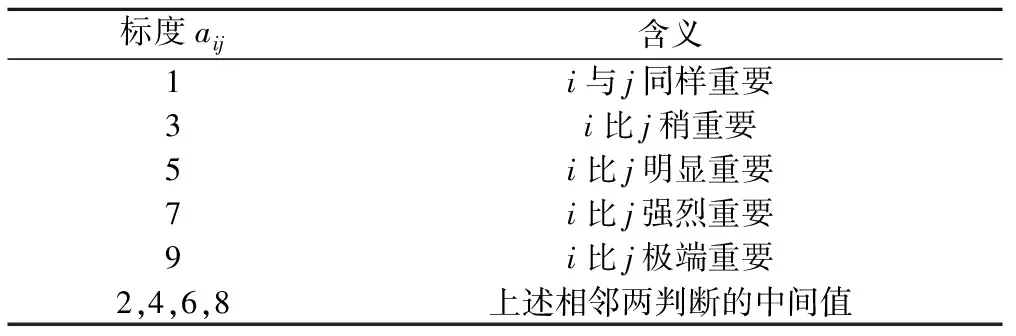
表1 AHP標度法及其含義Tab.1 Grade dividing of AHP and its meaning

判斷矩陣為：

(5)

式中：aij(i,j=1,2,…,n)是第i個因素的重要性與第j個因素的重要性之比。

權重計算：采用方根法計算權重，并將結果歸一化，得到權重向量，計算公式如下：

(6)

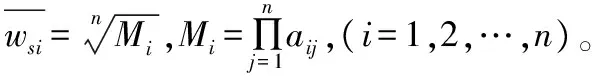
判斷矩陣的一致性檢驗：

評價判斷矩陣的一致性檢驗指標為：

(7)

式中：n為判斷矩陣的階數；λmax為A的最大特征根。

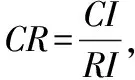
2.3.2熵權法

熵權法是在客觀條件下，有評價指標值構成的判斷矩陣來確定指標權重的一種方法，它能盡量消除各因素權重的主觀性，是評價結果更符合實際[8]。計算步驟如下：

原始數據為由n個評價指標，m個評價對象形成的n×m矩陣，即：

(8)

標準化后得到判斷矩陣：

(9)

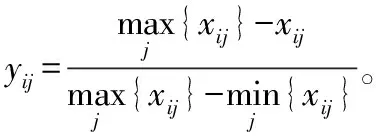
計算第i個指標的熵：

(10)

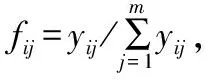
(11)

計算指標的熵權：

(12)

2.3.3綜合權重

將AHP法和熵權法計算得到的權重相結合，計算第i個指標的綜合權重為：

(13)

2.4 模糊綜合評價結果分析

將權重向量W與模糊關系矩陣R得到隸屬度向量B，再計算級別特征值P，即級別變量j與對應的隸屬度bj的乘積之和。計算公式為：

(15)

式中：bj為第j級標準對應的隸屬度。

3 結果與分析

3.1 水質評價計算過程

對白城市2013年20個地下水水質樣本的9個評價指標進行地下水水質評價，水質數據見表2。

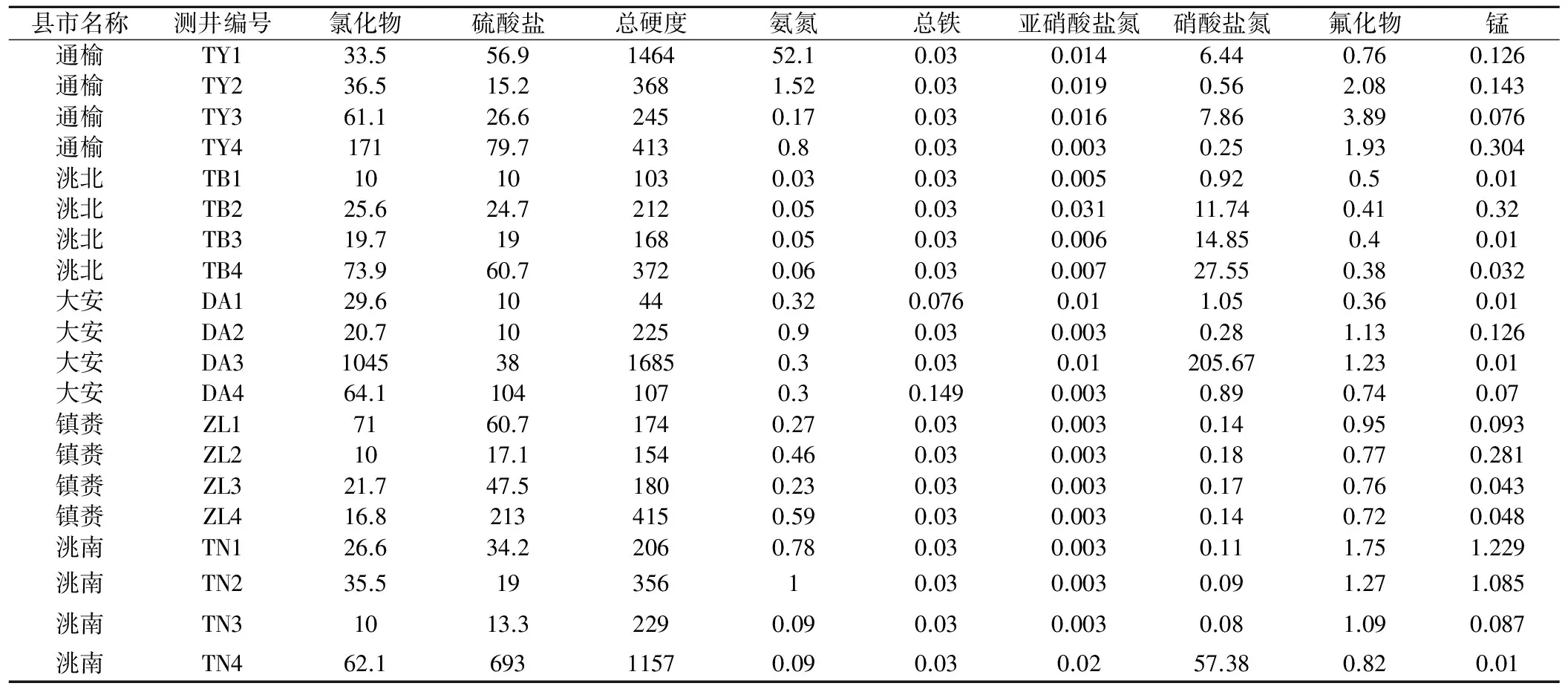
表2 2013年白城市地下水水質數據 mg/L

3.1.1建立模糊關系矩陣

以監測井TY1為例，計算得到的模糊關系矩陣為：

3.1.2確定指標權重

(1)AHP法。根據專家對當地水文地質情況，給出的評價指標的重要性排序，得到如下判斷矩陣：

根據公式(6)，計算得到權重Wsi：

Wsi=(0.028 5，0.043 5，0.070 8，0.070 8，

0.113 8，0.043 5，0.270 3，0.179 4)

判斷矩陣最大特征值：λmax=9.15，由公式(7)，計算得到一致性指標CI：CI=0.018 75，CR=0.012 93 <0.1，因此權重的確定是合理的。

(2)熵權法。根據表2數據和公式(8)-(12)計算得到熵權Wei:

Wei=(0.137 5，0.083 6，0.107 5，0.066 9，

0.139 6，0.139 7，0.079 3，0.178 8，0.067 1)

(3)綜合權重。由公式(13)，計算得到綜合權重：

Wi=(0.031 4，0.029 2，0.061 0，0.038 0，

0.200 9，0.127 6，0.027 7，0.387 6，0.096 6)

3.1.3模糊綜合評價

由公式(14)、(15)計算得到各水樣的級別特征值，計算結果見表3。

3.2 計算結果分析

本文采用AHP法與熵權法相結合的綜合權重法來確定模糊綜合評價的權重，為了檢驗這種評價方法的準確性和適用性，將其評價結果與內梅羅指數法的評價結果相比較。表3的對比結果顯示，兩種評價方法結果一致性很高，可以達到75%，同時結果不同的樣本評價等級差異很小。引起差異的主要原因為在綜合權重的確定過程中，AHP法是專家根據當地具體水文地質情況給出的各評價指標的重要性排序，而熵權法是通過分析整體的水質樣本，通過降低異常值對評價結果的影響，確定各評價指標在決策中貢獻的有效信息量。這兩種方法相結合確定的權重中，氟化物、總鐵、亞硝酸鹽氮以及錳這幾種評價指標的權重較大，因此其在水樣中的含量對水質評結果影響較大；而內梅羅指數法忽視了各指標權重對水質評價結果影響的差異性，在計算過程中過分夸大某些高濃度離子在水質評價中的影響，且未考慮到氟化物、總鐵等對身體有害的指標的側重。此外，引入級別特征值的概念，解決了最大隸屬度原則具有條件性的問題，更使水質評價結果具有連續性。從表3的結果中，洮北的水質相對較好，通榆的水質相對較差。通榆主要污染物為總硬度、氨氮、氟化物和錳。

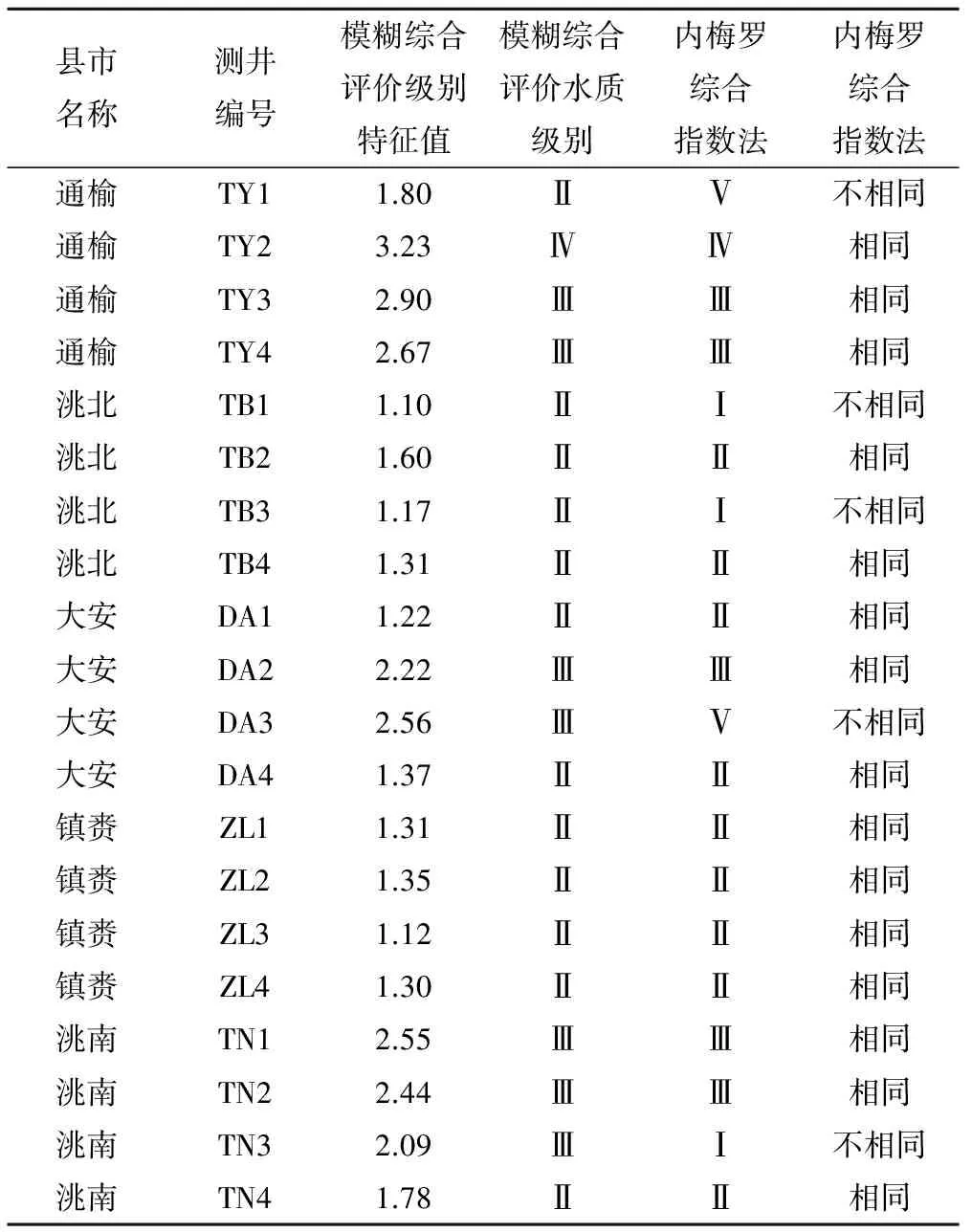
表3 模糊綜合評價法計算結果Tab.3 The result of fuzzy comprehensive evaluation

4 結 語

(1)本文采用AHP-熵權法對白城市20個地下水水質樣本進行模糊綜合評價。評價結果中，洮北的水質相對較好，通榆的水質相對較差。影響通榆縣地下水的主要污染因子為總硬度、氨氮、氟化物和錳。

(2)兩種評價方法對比，結果一致性很高達75%，利用AHP法和熵權法對地下水進行模糊評價的結果具有較好的準確性和適用性。基于AHP-熵權法的模糊綜合評價法在權重的確定上，具有主客觀相結合的優點，既充分利用了專家的經驗知識，又有效降低主觀因素的影響，充分考慮了不同水質指標在地下水水質評價中的差異性和整體性，使評價結果更加準確、合理，引入級別特征值的概念，解決了最大隸屬度原則具有條件性的問題，使水質評價結果具有連續性。

[1] 肖長來，梁秀娟．水環境監測與評價[M]. 北京：清華大學出版社，2008．

[2] 管延海，李 強，柴成繁. 模糊數學方法在天津市地下水水質評價中的應用[J]. 地下水，2008,(2):27-28,87.

[3] Zhou Yahong,Hao Gangli,Chen Kang,et al. Water quality evaluation based on fuzzy mathematics in groundwater resource area of SuoLuoShu in Shan Dong Province[J]. Advanced Materials Research, 2014,838-841:1 768-1 771.

[4] Han Lu,Song Yonghui,Duan Liang,et al. Assessment methodology for Shenyang Chemical Industrial Park based on fuzzy comprehensive evaluation[J]. Environmental Earth Sciences,2015,73(9):5 185-5 192.

[5] 盧文喜，李 迪，張 蕾. 基于層次分析法的模糊綜合評價在水質評價中的應用[J]. 人民黃河，2015，37(5):77-79.

[6] Pan Jun,Li Boyao,Jiang Mingcen. Improved fuzzy equilibrium average type comprehensive evaluation method in the application of water quality evaluation[J]. Advanced Materials Research, 2013,779-780 :1 619-1 622.

[7] 許 斌.白城市地下水資源保護研究[D].長春：吉林大學，2010.

[8] T L Satty. The Analytic Hierarchy Process[M]. New York: McGraw-Hill, 1980.

[9] 張先起，梁 川，劉慧卿. 基于熵權的屬性識別模型在地下水水質綜合評價中的應用[J]. 四川大學學報(工程科學版)，2005,(3):28-31.