淺談數學中函數定義域優先問題
江西省豐城中學 張 璐
淺談數學中函數定義域優先問題
江西省豐城中學 張 璐
思維品質是指個體思維活動特殊性的外部表現。它包括思維的嚴密性、思維的靈活性、思維的深刻性、思維的批判性和思維的敏捷性等品質。函數作為高中數學的主線,貫穿于整個高中數學的始終。
函數關系式 函數最值 函數值域 函數單調性 函數奇偶性
一、函數關系式與定義域
函數關系式包括定義域和對應法則,所以在求函數的關系式時必須要考慮所求函數關系式的定義域,否則所求函數關系式就可能是錯誤的。如:
例1:某單位計劃建筑一矩形圍墻,現有材料可筑墻的總長度為100m,求矩形的面積S與矩形長x的函數關系式?
解:設矩形的長為x米,則寬為(50-x)米,由題意得:S=x(50-x),
故函數關系式為:S=x(50-x).
如果解題到此為止,則本題的函數關系式還欠完整,缺少自變量x的范圍。也就是說學生的解題思路不夠嚴密。因為當自變量x取負數或不小于50的數時,S的值是負數,即矩形的面積為負數,這與實際問題相矛盾,所以還應補上自變量x的范圍:0 即:函數關系式為:S=x(50-x)(0 函數的值域是該函數全體函數值的集合,當定義域和對應法則確定,函數值也隨之而定。因此在求函數值域時,應注意函數定義域。如: ∴y=2(t2+3)-5+t=2t2+t+1 剖析:經換元后,應有t≥0,而函數y=2t2+t+1在[0,+∞)上是增函數, 所以當t=0時,ymin=1. 故所求的函數值域是[1,+∞). 函數單調性是指函數在給定的定義域區間上自變量增加時,函數值隨著增減的情況,所以討論函數單調性必須在給定的定義域區間上進行。 判斷函數的奇偶性,應先考慮該函數的定義域區間是否關于坐標原點成中心對稱,如果定義域區間關于坐標原點不成中心對稱,則函數就無奇偶性可談。否則要用奇偶性定義加以判斷。 綜上所述,在求解函數關系式、最值(值域)、單調性、奇偶性等問題中,若能精細地檢查思維過程,思辨函數定義域有無改變(指對定義域為R來說),對解題結果有無影響,就能提高學生質疑辨析能力,有利于培養學生的思維品質,從而不斷提高學生思維能力,進而有利于培養學生思維的創造性。二、函數值域與定義域
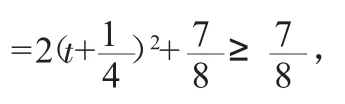
三、函數單調性與定義域
四、函數奇偶性與定義域

