基于分形特征的同步器齒環缺陷識別研究

賴科學, 李燦燦, 陳　朗, 何　濤

(湖北工業大學現代制造質量工程重點實驗室， 湖北 武漢 430068)

?

基于分形特征的同步器齒環缺陷識別研究

賴科學, 李燦燦, 陳朗, 何濤

(湖北工業大學現代制造質量工程重點實驗室， 湖北 武漢 430068)

[摘要]通過展開同步器齒環(齒環)內輪廓，發現其具有不規則、統計自相似性和相對平滑的特征。采用分形理論中的分形維數(FD)對其進行缺陷識別。首先，用結構函數法對(Weierstrass-andelbort)W-M函數模型進行分析，可得結構函數法計算相對平滑曲線的維數誤差小；然后，基于齒環內輪廓展開曲線相對平滑的特性，采用結構函數法對正常和缺陷齒環內輪廓展開曲線進行分維計算。實驗結果表明，正常齒環內輪廓展開線的分維不同于缺陷齒環的分維，從而通過維數差異實現對正常和缺陷齒環的識別。

[關鍵詞]同步器齒環； 結構函數法； W-M函數； 分維

缺齒、缺耳以及齒形不規則等缺陷是困擾汽車變速箱中同步器齒環制造質量的重要問題之一[1-2]。通過對齒環內輪廓展開曲線的觀察與分析，發現其具有不規則和統計自相似性特征。因此，本文采用分形理論方法對缺陷齒環進行識別。分形理論[3]用于物體輪廓缺陷識別，一般用分形維數(FD)對其進行定量描述，實現物體輪廓的有效表征。在進行物體輪廓的分形表征時，必須選擇適當的維數計算方法。目前，計算物體表面輪廓分形維數的方法有盒維計數法、尺碼法、方差法、均方根法和結構函數法[4]等，以上方法都有各自的特點和適用范圍，如果采用的分形維數計算方法與實際分形集合的類型不相符，就會產生較大的計算誤差。研究表明，齒環內輪廓展開線的維數范圍一般在1.2~1.3之間。基于齒環內輪廓展開曲線維數較小的特征和結構函數法計算維數較小輪廓誤差小的特點，結構函數法能夠很好地識別缺陷齒環輪廓。本文首先用結構函數法計算W-M函數圖像的維數，分析其使用范圍；再根據齒環內輪廓展開線的特征，用結構函數法進行分維計算和比較，實現對正常和缺陷齒環的識別。

1結構函數法

設測量的輪廓高度為采樣點數的任意增量，將表面輪廓曲線視為一個時間序列Z(x),則具有分形特征的時間序列能使其采樣數據的結構函數滿足[5]

S(f)=[Z(x+f)-Z(x)]2=Cf4-2D

(1)

式中:[Z(x+f)-Z(x)]2表示差方的算術平均值,f是數據間隔的任意選擇值。針對若干尺度f對輪廓曲線的離散信號計算出相應的S(f),然后在對數坐標中得logS~logf直線的斜率T,如此，則分形維數D與斜率T的轉換關系為

(2)

2W-M函數及分形測度驗證

2.1W-M函數曲線

W- M 函數是連續且不可微的函數演變而成的。W -M 分形函數可用于刻畫表面輪廓[6]。1991 年, M.Majumdar與B. Bhushan提出了對原W -M函數的修正，其公式為

(11)

(3)

其中：x表示輪廓的水平位置坐標，Z(x)為隨機表面輪廓高度，D為輪廓分形維數，G是特征尺度系數，γn表示輪廓的空間頻率，γ為大于1的常數，nl為輪廓最低截止頻率相對應的系數。

2.2W-M函數曲線設計

W- M函數曲線屬于標準分形函數曲線,它的理想分形維數為D。由式(3)知,W-M函數主要由模型D、G、γ、n所決定,取G=0.01，γ=1.5，n=1000,x在[0. 6,0. 7]取值，Δx=0.001。D=1.1，D=1.5，D=1.8時，其模擬結果如圖 1所示。

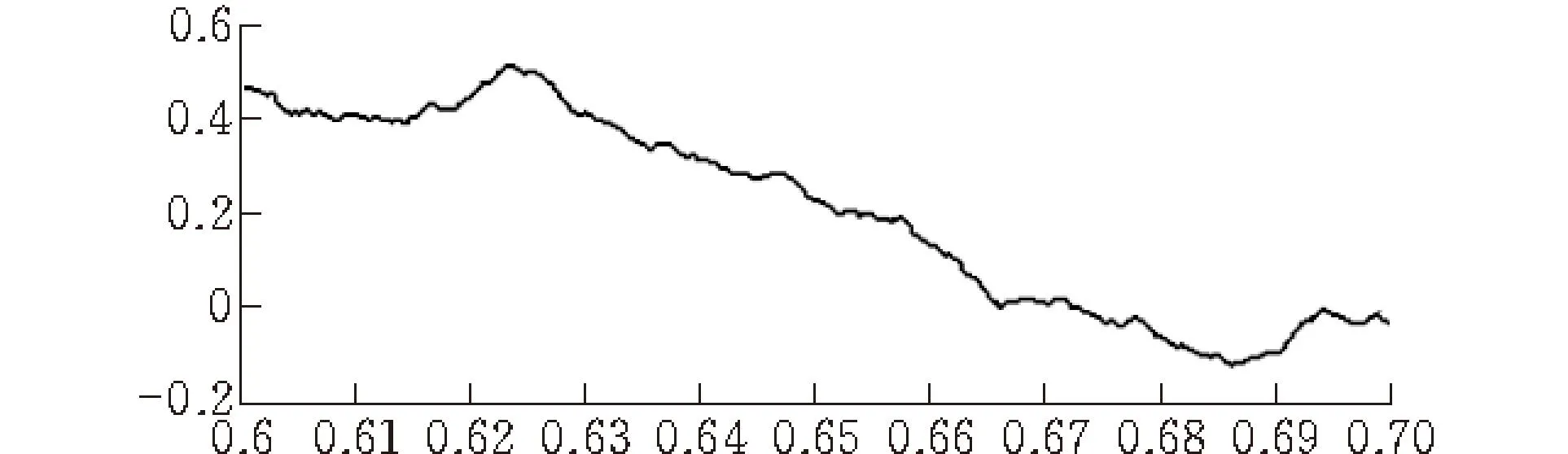
(a)D=1.1

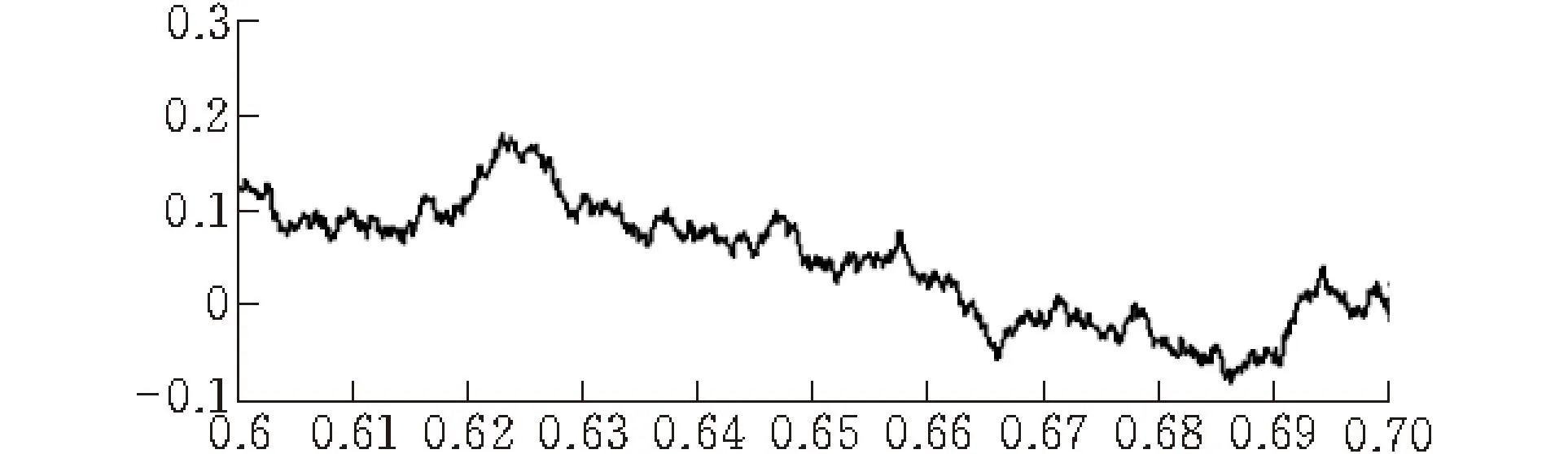
(b)D=1.5

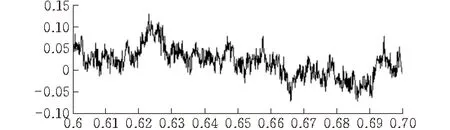
(c)D=1.8圖 1　W-M函數曲線

2.3結構函數法對W-M函數的分形驗證

通過結構函數法對圖1中的曲線進行維數計算，其中數據間隔f分別取2，4，8， …， 2n。圖2中分別表示了結構函數計算理論分形維數為1.1、1.5、1.8的測度-尺度的雙對數關系，其對應擬合直線的斜率T分別為1.7289、1.1035、0.6546。通過式(2)，可得到函數結構法計算W-M函數曲線維數(表1)。

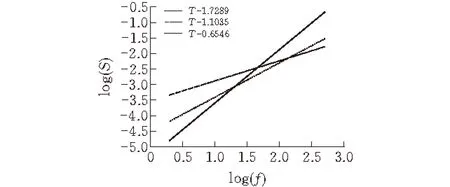
圖 2　W-M函數曲線的雙對數擬合直線

理論維數實際計算維數相對誤差/%D=1.1d=1.13553.23D=1.5d=1.44803.47D=1.8d=1.67277.07

由表1可知，當曲線的理論分形維數越小時，結構函數法計算值越接近理論值，隨著曲線的維數增加，其計算結果誤差越大。實驗結果表明，結構函數法針對輪廓曲線較為平滑的分形維數計算結果誤差越小，輪廓曲線就越復雜，其計算結果誤差亦越大。

3結果函數法對齒環輪廓分形維度測定

3.1齒環采集系統

齒環樣本圖像的采集系統如圖3所示。相機安裝于齒環正上方，在齒環下面放置一個背光源，并距離齒環上端100 mm處放置一個環形光源。這種圖像采集系統能較好地去除噪聲，保留齒環的輪廓和表面信息。對樣本1(正常齒環)和樣本2(缺陷齒環)進行圖像采集，采集圖像大小為512×512，采集樣本圖像如圖4所示。

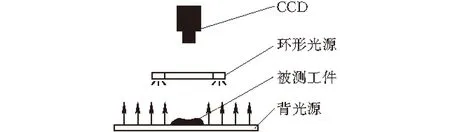
圖3　圖像采集系統

圖 4　齒環樣本原始圖像

3.2齒環內輪廓展開流程

對齒環內輪廓進行維數計算時，需要先對其進行預處理并展開，再用結構函數法計算其展開后曲線的維數，其計算流程如圖5所示。

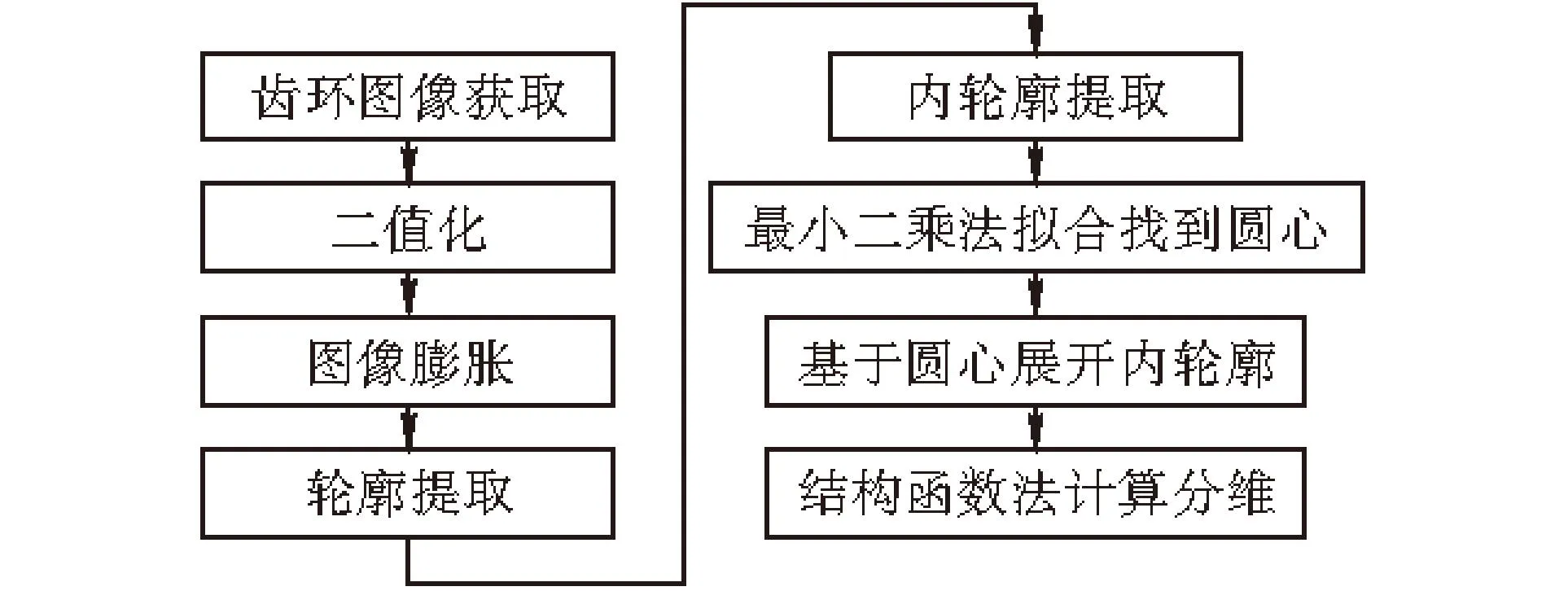
圖 5　齒環內輪廓維數計算流程圖

現以樣本1圖像為例，詳細說明其維數的計算。首先對樣本圖像進行二值化，結果如圖6a所示。直接對二值圖像進行輪廓提取會存在齒環內部細小輪廓，需要對其進行膨脹處理，其計算公式為

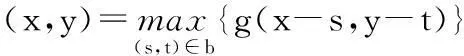
(4)

式中：b(s,t)為平坦結構元，[g⊕b](x,y)為圖像g中與b重合區域的最大值。對膨脹后圖像進行輪廓提取，獲得齒環內輪廓圓，并采用最小二乘法擬合最接近齒環輪廓提取線的基準圓，計算得到該基準圓的圓心坐標(x0,y0)[7]。

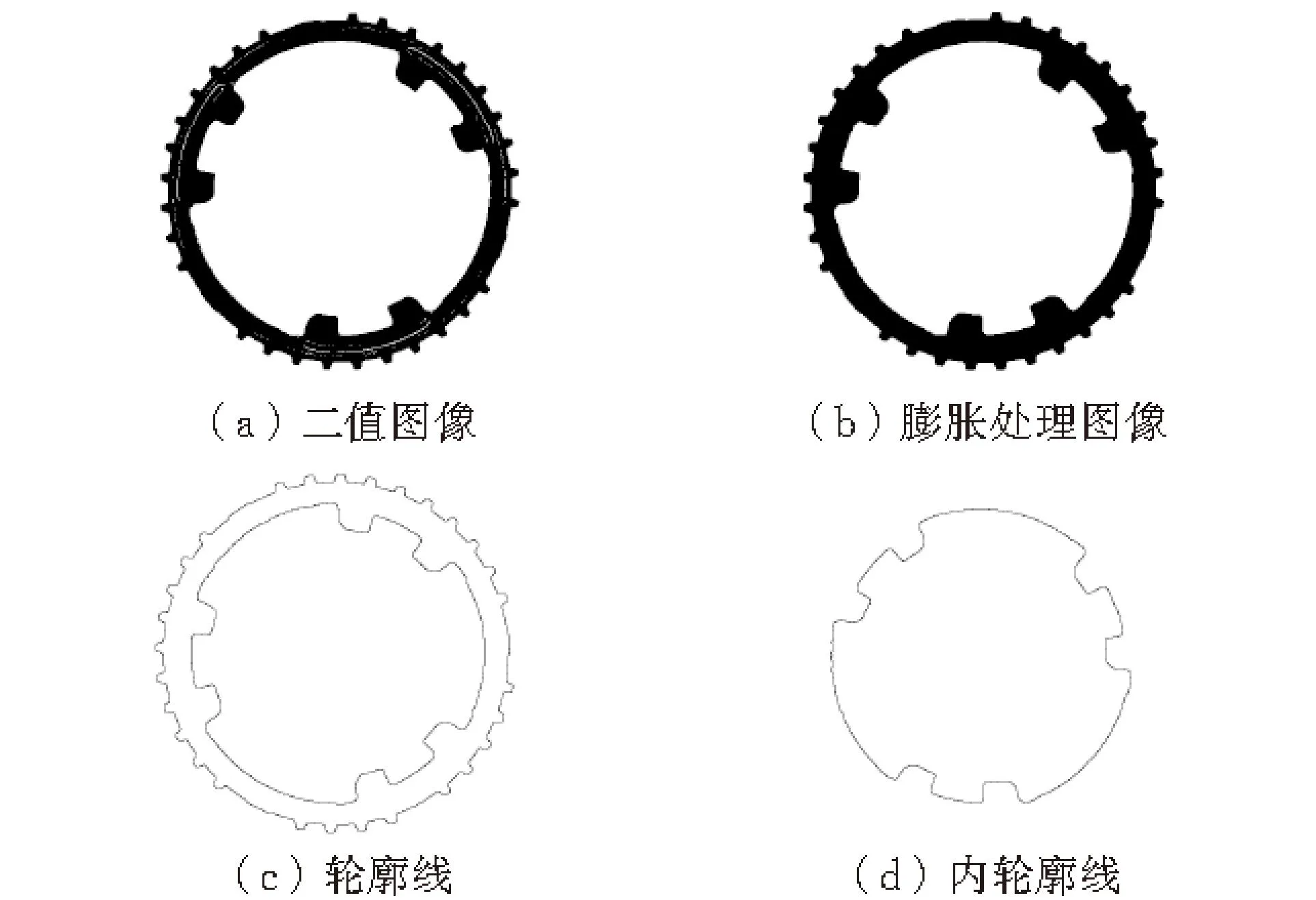
圖 6　齒環樣本1預處理

(5)

找出這一系列R值中的最小值

(6)

則展開后輪廓曲線上所有點的高度

h=R-Rmin+1

(7)

根據式(5)-(7)對樣本1和樣本2的內輪廓進行展開，得到樣本的內輪廓展開曲線如圖7所示。

圖 7　齒環內輪廓展開曲線

3.3齒環維數計算與分析

用結構函數法對樣本1內輪廓展開線進行分形維數計算，當數據間隔f為10，得到測度-尺度的雙對數離散點(圖8)。可見所有離散點成曲線分布，其擬合直線的斜率T不能準確表示分維D。通過實驗分析，本文選取前30個離散點進行線性擬合(圖9)，得到擬合直線的斜率T為1.659 0，并通過式(2)計算出齒環內輪廓展開線的分形維數D為1.170 5。

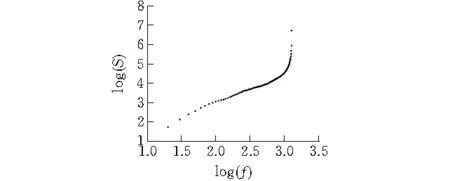
圖 8　所有的點的分布圖

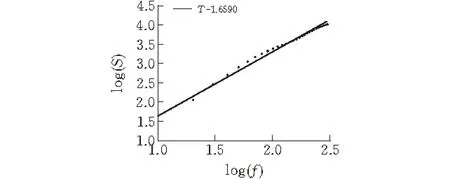
圖 9　前30個點的雙對數擬合圖

用結構函數法對9組正常和缺陷齒環內輪廓展開曲線樣本進行維數計算，結果如表2所示。正常組和缺陷組齒環的平均維數分別為1.174 5和1.154 0，動態范圍分別為±0.005 9和±0.007 3。根據表3中改進差分盒維法的計算結果得到分布趨勢(圖10)。正常組齒環的維數大于缺陷組齒環，兩者存在一定間距，且各自平穩，能夠實現正常和缺陷齒環識別。

表2　正常和缺陷齒環內輪廓展開曲線的維數

圖10　齒環分形維數對比圖

4結論

1)結構函數法對輪廓曲線分形維數計算結果誤差隨著曲線復雜度的增加而增大。

2)結構函數法可以用于區別正常和缺陷齒環，且具有一定的穩定性，具工程應用價值。

[參考文獻]

[1]李四年,陳園,葉甲旺,等.汽車同步器齒環的生產現狀與發展前景[J].湖北工業大學學報,2012,01:114-116.

[2]Chen Q， Ma Y B， Huang S W，et al.Research on gears’ dynamic performance influenced by gear backlash based on fractal theory[J]. Applied Surface Science，2014， 313 : 325.

[3]Mandelbrot B . The Fractal Geometry of Nature, Henry Holt and Company[M],New York: henry holt & co, 1983.

[4]朱華,葛世榮.結構函數與均方根分形表征效果的比較[J].中國礦業大學學報,2004(04):34-37.

[5]李超,焦瑜,張靜,等. PEEK摩擦信號分形維數與表面形貌相關性試驗研究[J]. 中國機械工程,2011(14):1715-1719.

[6]喬忠云.基于Matlab復合材料磨損表面形貌W-M分形模型及其模擬[J].煤礦機械,2007(10):37-38.

[7]趙樹茂,梅國暉,胥勇,等.基于分形特征的鋼水連續測溫傳感器損傷診斷[J].儀器儀表學報,2013(04):728-735.

[8]Gonzalez Rl C， Woods R E. Digital Image Processing [M]. Third Edition.北京： Publishing house of electronics industry,2011：428-429.

[責任編校： 張眾]

Synchronizer Gear Ring Defect Recognition Based on Fractal Characteristics

LAI Kexue, LI Cancan, CHEN Lang, HE Tao

(HubeiKeyLabofModernManufactureQualityEngin.,HubeiUniv.ofTech.,Wuhan430068,China)

Abstract：Through expanding the synchronizer gear ring (gear ring) outline, the paper found that it has an irregular, statistical self-similarity and relatively smooth features, using fractal dimension (FD) of fractal theory for defect identification. Firstly, the study analyzed the (Weierstrass-andelbort)W - M function model using the structure function method, concluding that the error is small after using such a method to calculate the fractal dimension of the smoother contour curve. Secondly, since the gear ring contour curve is relatively smooth, the structure function method was adopted to calculate the fractal dimension of inner outline curve of normal and defect gear rings. Experimental results show that fractal dimension of normal gear ring inner contour line is greater than the defects, implementing the dimension identification of normal gear and defect rings.

Keywords：synchronizer gear ring; structure function method; W-M function；fractal dimension

[中圖分類號]TP391.4

[文獻標識碼]：A

[文章編號]1003-4684(2016)01-0008-04

[作者簡介]賴科學(1990-)， 男， 四川隆昌人，湖北工業大學碩士研究生，研究方向為圖像處理技術

[基金項目]國家自然科學基金(51275158)

[收稿日期]2015-11-16