大水滴撞擊壁面的動態特性數值模擬

郭宇翔，劉蔭澤，董威，雷桂林，朱劍鋆

(上海交通大學機械與動力工程學院，上海200240)

大水滴撞擊壁面的動態特性數值模擬

郭宇翔，劉蔭澤，董威*，雷桂林，朱劍鋆

(上海交通大學機械與動力工程學院，上海200240)

采用VOF方法建立了大水滴撞擊壁面的計算模型，模擬了大水滴以不同直徑、不同速度撞擊光滑壁面的動態撞擊過程和撞擊特性。計算結果表明:在大韋伯數情況下，水滴撞擊光滑壁面會在鋪展過程中發生邊緣水滴飛濺;在水滴撞擊壁面的收縮階段，隨著水滴直徑的減小和水滴速度的提高，會發生液膜緩慢收縮、邊緣液環和液膜分離、中心處部分液膜和邊緣液膜分離、液膜完全破裂等不同結果;當水滴直徑和撞擊速度增大時，同一時刻水滴的鋪展半徑、最大鋪展半徑、最大鋪展系數增大;水滴在壁面上達到最大鋪展系數所用的無量綱時間隨水滴直徑增大而增大，同一直徑水滴不同初始速度下達到最大鋪展系數所用的無量綱時間變化較小。

大水滴;數值模擬;VOF方法;撞擊特性;水膜

0 引言

飛機及發動機結冰是危及飛行安全的嚴重問題，與結冰有關的飛行事故每年都有發生。當飛機穿越含有過冷水滴的云層時，過冷水滴撞擊到飛機機翼以及發動機的進氣部件表面，極易發生凍結。飛機及發動機部件結冰會改變部件的氣動性能，對飛機造成極大的安全隱患。融化的冰如果被發動機吸入，會導致發動機葉片的機械損傷，引起發動機熄火停車，造成致命后果。

飛機結冰和防冰過程涉及了復雜的多相流動換熱過程，其撞擊水滴凍結過程的數學模型至今仍不完善。有關飛機結冰和防冰過程中大水滴撞擊、水膜的流動與換熱、結冰引起的表面粗糙度對流動換熱的影響等研究工作在近年來得到了研究人員的廣泛關注［1-6］。過冷水滴撞擊特性是飛機結冰和防冰分析的基礎。通常，直徑小于50μm的過冷水滴不考慮其在運動及撞擊過程中的變形，在撞擊機翼表面后不發生飛濺脫離現象。對于小水滴在機翼表面的撞擊可以較為準確地采用拉格朗日方法和歐拉方法做出預測［7-8］。而直徑大于50μm的過冷水滴通常稱為過冷大水滴(Supercooled Large Droplets，SLD)。大水滴在撞擊飛機迎風表面后，會發生飛濺、反彈、二次撞擊等多種情況。大水滴的破碎和飛濺會使得撞擊水滴的直徑和部件表面的水收集系數發生變化，從而影響部件表面生成的冰型。對于飛機結冰分析中大水滴的撞擊特性，目前主要還是采用實驗數據總結的經驗模型進行計算分析［9-10］。由于SLD撞擊特性的復雜性，目前還沒有一個經驗模型在各種結冰條件下都可以給出滿意的撞擊特性預測結果。因而對SLD撞擊過程的機理研究還是非常迫切且必要的。

高速攝像技術的出現為大液滴撞擊表面的實驗研究提供了強有力的支持。近年來許多研究人員利用高速攝像技術和液滴生成裝置研究了液滴撞擊形態的變化。Thoroddsen等［11］、Yarin等［12］通過實驗方法拍攝了液滴撞擊壁面后的鋪展、快速濺射、冠狀濺射、收縮濺射、部分回彈、完全反彈等多種結果。Rioboo等［13］著重研究了壁面浸潤性及表面張力對液滴撞擊壁面鋪展的影響。Pan等［14］研究了不同屬性的液滴撞擊不同粗糙度的固體表面的飛濺情況，通過高速攝像裝置拍攝了大韋伯數(We數)液滴撞擊壁面發生放射狀飛濺和日冕皇冠狀飛濺，發現當韋伯數足夠大時即使在光滑壁面上也能發生液滴飛濺。Tsai等［15］實驗研究了微納米超疏水表面對液滴撞擊的影響。液滴撞擊的實驗研究也具有很大的局限性，通過高速攝像只能得到不同時刻的液滴撞擊的形態圖片，液滴撞擊過程中的速度分布、壓力分布、換熱情況等均不能測出。同時由于高速液滴撞擊實驗條件實現困難，目前大量進行的液滴撞擊試驗的初始速度一般小于40m/s。

理論研究方面，Naber和Reitz［16］在類比射流噴射的基礎上考慮了液滴破裂、液滴碰撞、液滴融合以及空氣渦流，提出了著名的N-R模型，認為韋伯數決定了液滴碰壁后形態變化。Rioboo等［17］定義了液滴撞擊壁面后的幾種不同狀態:沉積、回彈、部分回彈、迅速飛濺、冠狀飛濺、收縮破裂。Cossali等［18-19］、Pan和Law［20］、Pan等［21］通過大量實驗及數據分析確定了液滴撞擊濕表面不同形態結果的臨界韋伯數。數值模擬方面，Gunjal等［22］使用VOF(Volume of Fluid)方法模擬了液滴撞擊壁面的過程，并通過實驗驗證了VOF模型模擬液滴撞擊壁面結果的可行性。Kim等［23］使用VOF模型數值模擬了不同速度、流變參數、表面張力條件下的液滴撞擊壁面，結果表明液滴的鋪展形態取決于雷諾數和韋伯數，液滴的收縮形態決定于毛細數、Bingham-Capillary數，并預測了液滴撞擊壁面的最大鋪展半徑。Bussmann等［24］使用三維模型研究了液滴撞擊不對稱表面過程中的動態壁面接觸角的影響，在模擬液滴撞擊傾斜壁面時使用了實驗測得的液滴鋪展動態壁面接觸角作為壁面邊界條件，與實驗結果較為符合，并在此基礎上提出了一種新的給定動態接觸角的方法。梁超［25］使用三維模型和VOF方法研究了液滴低速撞擊等溫壁面過程中的壁面接觸角、液滴初始速度、表面張力系數、液滴動力粘度等的影響及液滴撞擊熱壁面的換熱特性，此外還使用二維軸對稱模型模擬了不同液滴初始速度、表面張力系數、液滴動力粘度、初始液膜厚度等條件下的液滴撞擊液膜過程。賈小娟［26］使用三維模型完成了雙液滴垂直及斜向撞擊液膜的數值研究。Burtnett［27］使用二維軸對稱模型模擬了50 μm液滴撞擊微結構表面，對于干表面和滲透表面得到了不同的液滴撞擊結果。Tan等［28］采用大水滴破碎、飛濺、反彈模型進行了結冰翼型表面的水滴撞擊特性計算，并與試驗結果進行了對比驗證。

針對飛機結冰所涉及的SLD直徑范圍內的水滴高速撞擊壁面和液膜的研究較少。本文借助VOF方法開展了大水滴撞擊壁面過程的動態數值模擬研究，分析了大水滴撞擊過程中形態變化、飛濺現象以及撞擊特性，數值模擬結果加深了對飛機表面過冷大水滴撞擊過程物理機理的理解。

1 計算模型

1.1 計算模型

結冰云層中SLD直徑分布大致在50 μm到500μm的范圍內。大水滴撞擊飛機表面后會發生飛濺、反彈、二次撞擊、鋪展-收縮-振蕩等多種情況。當飛機表面聚集的水滴足夠多時，水滴會在飛機表面形成一層液膜，隨后還會發生大水滴撞擊薄液膜的情況。

數值模擬中采用二維軸對稱模型，計算區域為矩形區域，中間為對稱軸，底面為壁面邊界條件。對于大水滴高速撞擊壁面的數值模擬，為了能夠細致地計算出水滴的形態變化，要求計算區域的網格足夠密集，使用二維軸對稱模型能有效地減小網格數量，縮短計算時間。水滴撞擊表面的幾何模型如圖1所示。

圖1 水滴撞擊壁面的幾何模型Fig.1 Geometric model of drop let im pingement

在數值模擬中采用的二維軸對稱模型，考慮了一些流體流動過程中的三維效應，能在一定程度上代替三維網格。在水滴低速撞擊的很多文獻中均使用二維軸對稱模型模擬三維的液滴撞擊壁面和液滴撞擊液膜。相對于三維模型，二維軸對稱模型認為流動過程中只存在沿徑向的梯度，沿周向均勻分布，因此二維軸對稱模型不能夠完整捕捉液滴撞擊壁面過程中出現的沿周向不均勻、不連續的現象。但使用二維軸對稱網格模擬液滴撞擊壁面，計算得到的液滴的鋪展系數、液膜厚度等數據可信度高，同時能夠捕捉到液滴鋪展和收縮過程中的二次液滴飛濺、液膜斷裂等現象。

1.2 VOF模型

大水滴高速撞擊壁面的數值模擬，是一種水-空氣的兩相流動分析。數值追蹤兩相流界面的方法包括Level-Set方法、粒子標記方法、VOF方法等。其中VOF方法相對于其他的界面追蹤方法模型簡單，追蹤界面精確，能夠考慮界面融合和分離現象［29］。

Hirt和Nichols［30］提出的VOF方法，計算中通過引入流體體積分數α來標記界面兩邊不同相的流體，動態追蹤不同相的區域，采用界面重構技術來確定相界面。若假設計算域中共有n相流體，對于任意計算網格的第k相流體來說，其體積分數可能存在如下三種情況，即:

如果αk等于0，說明在這個網格內不含有第k相流體;如果等于1則說明在這個網格內只存在第k相流體;而如果αk處于0和1之間，表明這個網格內部同時存在多相流體。由于VOF模型假定多相流體不能混合，可以認為該網格處于多相流體界面或流體界面附近。根據體積分數的定義，在同一個網格內部，各相流體的體積分數和應該為1，即:

VOF方法在每一個網格內采用體平均來計算流動方程并通過流體體積分數捕捉相的界面，圖2為 VOF界面追蹤示意圖。

圖2 VOF界面追蹤示意圖Fig.2 Interface tracking diagram of VOF method

在本文討論范圍內，所涉及的流體相只包含空氣相和水滴相兩相，在每個計算網格中，第k相(k=1，2)的連續性方程可表示如下:

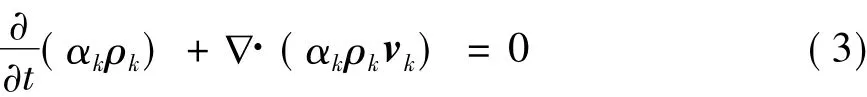
在VOF模型中，認為在相同位置處的不同相流體具有同樣的速度，因此對于空氣相和水滴相采用同一套動量方程進行求解:

其中，P為壓力，FSF為由表面張力引起的動量源項。式(4)中的物性參數ρ和μ采用體積加權平均法獲得:

1.3 表面張力模型

表面張力采用連續表面張力CSF(Continue Surface Force)模型，CSF模型將VOF計算中附加的表面張力處理為動量方程的源項。相界面兩側的內外壓差等于表面曲率和與表面張力系數之積:

式中，p1和p2分別為界面兩側的流體壓力，R1和R2為兩個主曲率半徑。

在水滴撞擊的過程中表面張力以及壁面浸潤性起著重要作用，正是由于表面張力的存在，水滴在撞擊壁面達到最大鋪展直徑后會發生收縮反彈、收縮振蕩或者液膜在表面張力作用下拉裂等現象。由于水滴撞擊過程中的動態接觸角難以測得，數值模擬中使用靜態接觸角代替動態接觸角。

水滴撞擊壁面是一個瞬態不可壓縮過程，數值模擬采用PISO算法。時間步長和空間步長的選取對于水滴撞擊特性的數值模擬非常重要，合適的空間步長和時間步長能夠用較少的時間得到精確的結果。空間步長的選取通過網格無關性驗證來確定。時間步長通過克朗數確定:

其中:d t為時間步長;d x為空間步長;Cr可以理解為內擴散相在單位時間內前進的距離與空間步長的比值，這里Cr取為0.25確定初始時間步長。

2 計算方法模型驗證

結冰云層過冷大水滴直徑為幾十到幾百微米，水滴撞擊速度很大，要保證計算過程中合適的Cr，需要的網格步長很小。如果選擇的網格較小，雖然能夠更精確、細致地計算出大水滴撞擊壁面后的形態變化，但是整個網格的數量將急劇增大，同時需要設定較小的時間步長，這樣整個模擬的時間將大大增長;如果選擇的網格步長過大，則不能精確地計算水滴撞擊壁面后的形態變化，計算結果偏差較大，相的界面不清晰。

大水滴高速撞擊的試驗數據很少，因此這里以水滴速度較低的試驗數據進行了計算方法的驗證。選取試驗條件水滴直徑2.6mm，水滴初始速度0.5m/s，壁面接觸角為160°作為對比算例。圖3為不同網格尺度下不同時刻水滴撞擊壁面后的相圖。圖4為撞擊區域網格尺度分別為0.02 mm、0.01 mm、0.0075 mm條件下水滴在壁面上的鋪展系數(d/D)隨無量綱時間(t·v/D)的變化曲線，其中d為水滴的鋪展直徑，D為水滴的初始直徑。通過對比發現，相同時刻0.01 mm與0.0075 mm網格的水相形態和水滴鋪展系數基本相同，而與0.02mm網格步長下的水滴形態差異相對較大。在本算例中，0.01mm是一個合適的網格步長，既能保證計算結果的精度，也能保證計算的速度，后面的模擬計算以此網格尺度所對應的無量綱網格尺度作為網格劃分的參考依據。

圖3 0.02mm、0.01mm、0.0075mm網格下的相圖(時間間隔為1m s)Fig.3 Comparison of droplet phase at grids of 0.02mm，0.01mm，and 0.0075mm(Δt=1ms)

圖4 0.02mm、0.01mm、0.0075mm網格步長下的鋪展系數變化曲線Fig.4 Spread coefficient curves at grids of 0.02mm，0.01mm，and 0.0075mm

圖5為數值模擬得到的相同時刻水滴撞擊壁面后的相圖與文獻［31］相同時刻實驗拍攝圖片的對比圖。通過對比發現，數值模擬得到的結果與文獻中實驗得到的結果基本相同，驗證了本文計算方法的可靠性。

圖5 水滴以0.5m/s速度撞擊接觸角為160°壁面的計算結果與文獻中實驗結果的對比圖Fig.5 Numerical simulation results compared w ith experimental results when a droplet impacts on surface at the velocity of 0.5m/s

3 計算結果及分析

數值模擬中大水滴直徑D選取500μm、300μm、100 μm和50 μm，水滴初始速度v0選取30 m/s、40m/s、50m/s、60m/s、70m/s。以鋁合金材料表面模擬飛機部件表面，壁面接觸角為75°。

3.1 大水滴直徑對撞擊特性的影響

研究在高速情況下不同直徑的水滴撞擊壁面特性時，保持水滴的初始速度為60m/s。觀察不同直徑下水滴撞擊壁面后的形態變化，分析水滴撞擊壁面后的鋪展系數及鋪展時間。

以250網格/直徑的網格模擬500 μm水滴撞擊壁面的動態過程，確定了水滴的最大鋪展半徑大約為2mm，因此取模型計算區域為3 mm×3 mm的對稱區域。由于使用該網格步長/直徑模擬時，鋪展液膜最薄處僅有2層網格的厚度。為了更精確地反映高速水滴撞擊壁面過程，對計算區域近壁面處進行了局部加密處理，使用400網格/直徑并采用漸密網格。貼近壁面的第一層網格高為0.1 μm，網格高度方向尺度增長率為1.01。

圖6為水滴以不同直徑撞擊壁面的鋪展半徑隨時間變化曲線。圖7為水滴以不同直徑撞擊壁面的鋪展系數隨無量綱時間變化曲線。圖8為水滴直徑與最大鋪展半徑及最大鋪展系數關系曲線。圖9為水滴直徑與達到最大鋪展對應時間的關系曲線。分析圖6～圖9可以看出:大水滴高速撞擊壁面時，隨著大水滴直徑的增大，同一時刻水滴的鋪展半徑和鋪展系數都增大，水滴達到最大鋪展對應的時間增大，對應的無量綱時間增大。

圖6 高速水滴以不同直徑撞擊壁面的鋪展半徑隨時間變化曲線Fig.6 Spreading radius curves of high velocity drop let im pacting on surface at different tim e

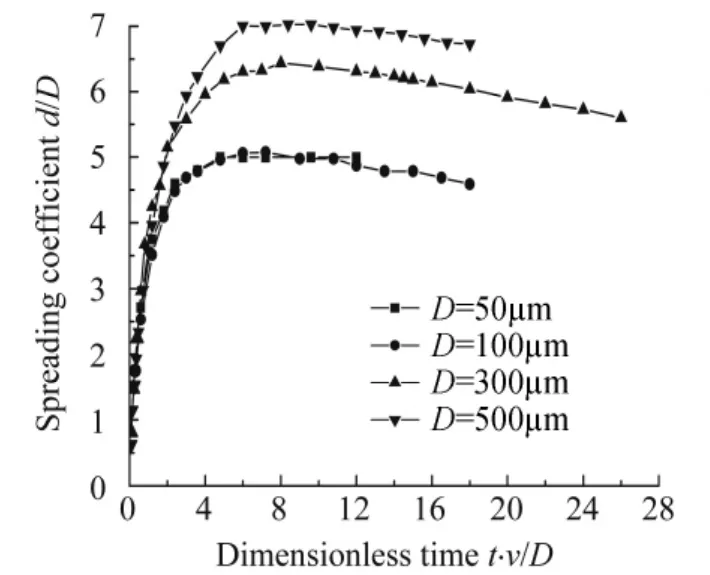
圖7 不同直徑撞擊壁面的鋪展系數隨無量綱時間變化曲線Fig.7 Spreading coefficient curves of drop let im pacting on surface at different dimension less time

圖8 水滴直徑與最大鋪展半徑及最大鋪展系數關系曲線Fig.8 Maximum spreading radius curve and maximum spreading coefficient curve varied w ith droplet diameters

圖9 水滴直徑與達到最大鋪展對應時間關系曲線Fig.9 Time-diameter curve and dimensionless time-diameter curve when the drop let reaches the maximum spreading radius

數值計算分析發現:大水滴以高速撞擊壁面時，水滴在壁面上的鋪展系數較大，中心液膜的厚度極薄，一般小于10μm;水滴直徑小于300μm時，液膜的收縮階段會發生液膜破裂;隨著水滴直徑的增大，在最大鋪展時刻對應的液膜厚度增大，水滴鋪展階段伴隨有部分水滴飛濺，飛濺的水滴直徑小于50 μm。當水滴初始直徑為500μm時，水滴在壁面上快速鋪展，在鋪展過程中有發生飛濺現象。由于撞擊的初始速度高，水滴鋪展系數大，達到最大鋪展系數時刻液膜的厚度只有7 μm。在表面張力的作用下，整個薄液膜逐漸收縮，但在收縮階段并沒有發生液膜拉斷的情況。隨著水滴初始直徑的縮小，水滴撞擊鋪展后的液膜厚度逐漸減小。在直徑為300 μm條件下，鋪展過程伴隨飛濺現象，由于達到最大鋪展系數時刻液膜較薄，在表面張力的作用下，收縮階段發生中心液膜拉斷現象;由于被拉斷的中心液膜面積較小，表面張力的回復作用不明顯，水滴形態變化所儲存的能量較少，表面張力在液膜收縮為中心小水滴過程中做功較少，中心液膜收縮形成的中心水滴具備的動能較低，中心水滴沒有脫離壁面發生反彈，而是在壁面上不斷振蕩。在水滴直徑為100 μm和50 μm條件下，由于鋪展的液膜厚度太薄，表面張力的作用更加劇烈，整個液膜被拉斷為多個部分，同時在表面張力的強烈收縮作用下，破裂液膜收縮形成的水滴伴隨有飛濺和反彈脫離壁面的情況。由上述分析可知，在水滴撞擊壁面達到最大鋪展后，水滴的形態變化達到最大，同時水滴的表面張力達到最大，薄液膜開始收縮。如果水滴鋪展形成的液膜厚度達到臨界值，在較大的表面張力作用下，液膜會被拉斷形成外圍的液環和中心的液膜;在極端情況下，整個液膜會形成多個外層液環甚至整個液膜被完全拉斷為不規則的多個部分(完全破碎)。表1給出了不同直徑大水滴撞擊壁面的液膜厚度及飛濺、破裂情況。

表1 不同直徑大水滴撞擊壁面的液膜厚度及飛濺、破裂情況Table 1 Film thickness、splashing and rupture of the impact of the large water drop lets w ith different diameters

3.2 大水滴速度對撞擊特性的影響

研究大水滴以不同速度撞擊壁面的特性時，保持水滴的直徑為300 μm，大水滴以初始速度分別為30 m/s、40m/s、50m/s、60m/s、70m/s。觀察不同初始速度的大水滴撞擊壁面后的形態變化，分析不同時刻水滴的鋪展半徑及飛濺現象。

圖10為不同速度下大水滴撞擊壁面后的局部放大相圖。圖11為不同速度的大水滴撞擊壁面后的鋪展半徑隨時間的變化曲線。圖12為不同速度的大水滴撞擊壁面后的鋪展系數隨無量綱時間的變化曲線。圖13為大水滴撞擊速度與最大鋪展半徑及最大鋪展系數關系曲線，圖14為大水滴撞擊速度與達到最大鋪展時間和達到最大鋪展對應無量綱時間的關系曲線。從圖11～圖14可以看出:大水滴高速撞擊壁面時，隨著大水滴初始撞擊速度的增大，同一時刻水滴的鋪展半徑和鋪展系數同時增大，水滴的最大鋪展半徑也增大，水滴達到最大鋪展對應的時間縮小，盡管水滴達到最大鋪展對應的無量綱時間相差不大，但達到最大鋪展時刻對應的液膜厚度減小。

圖10 不同速度下大水滴撞擊壁面后的局部放大相圖Fig.10 Enlarged pictures of droplet impacting on surface at different velocities

圖11 不同速度的大水滴撞擊壁面后的鋪展半徑隨時間的變化曲線Fig.11 Spreading radius curves of d rop let impacting on surface at different velocities

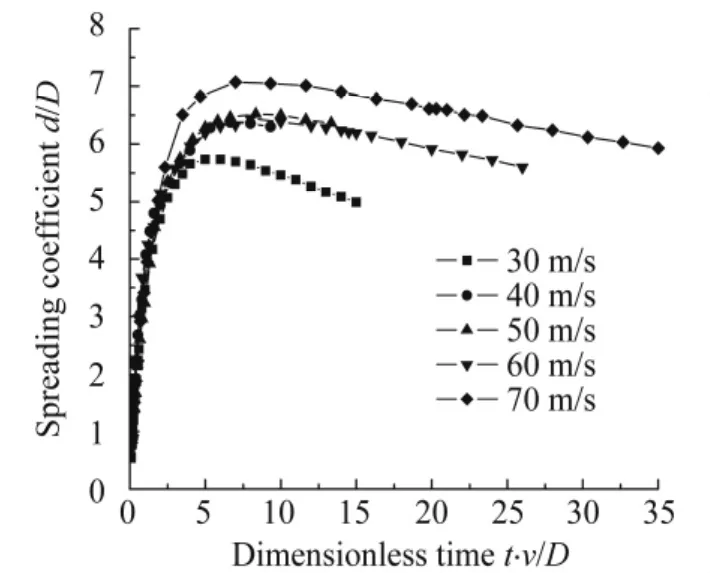
圖12 不同速度水滴撞擊壁面的鋪展系數隨無量綱時間的變化曲線Fig.12 Spreading coefficient curves of drop let impacting on surface at different velocities

圖13 大水滴撞擊速度與最大鋪展半徑及最大鋪展系數關系曲線Fig.13 M aximum spreading radius and maximum spreading coefficient varied w ith droplet velocities

圖14 大水滴達到最大鋪展半徑時對應的時間及無量綱時間Fig.14 Tim e-velocity curve and dim ension less time-velocity curve when the im pacting droplet reaches the maximum spreading radius

表2給出了不同速度的大水滴撞擊壁面后的液膜厚度及飛濺情況。初始速度為30 m/s的水滴具備的能量相對較低，撞擊壁面形成的液膜鋪展半徑較小，在液膜收縮階段不發生液膜斷裂;初始速度為40 m/s和50m/s的水滴具備的能量較高，液膜的鋪展半徑更大同時更不穩定，在液膜的收縮階段，邊緣液環與中心薄液膜連接處斷裂，初始速度為50 m/s的初始水滴形成的液膜更是斷裂為三部分;初始速度為60m/s和70m/s的水滴能量更高，在薄液膜的中心部位發生了液膜斷裂情況，中心液膜斷裂并聚集為一個小水滴不斷振蕩。這是因為:在表面張力的作用下，水滴撞擊壁面的收縮階段，水滴形成的液膜有向液膜中心收攏的趨勢。由于液膜邊緣處表面張力的作用最為強烈，液膜邊緣部分的水相率先向內運動，而液膜中心部位的水相運動趨勢不明顯，中心部位的液膜厚度基本不發生變化。邊緣液膜運動的結果是液膜的鋪展半徑變小，同時在液膜邊緣處水相堆積形成凸狀液環。

表2 不同速度的大水滴撞擊壁面后的液膜厚度及飛濺情況Tab le 2 Thickness of the liquid film and the sp lash of the large water drop lets impinging on surface at different speeds

4 結論

使用VOF方法數值模擬了直徑50～500 μm范圍內的大水滴以高速撞擊壁面的撞擊特性。通過改變大水滴的直徑和大水滴的初始速度，計算分析了不同條件下大水滴形態變化、撞擊結果以及鋪展系數的變化。

1)直徑50～500 μm的大水滴以高速撞擊壁面時，水滴在壁面上的最大鋪展系數較大，達到最大鋪展后的液膜厚度界于1～10μm之間。由于液膜的厚度很薄，在表面張力的作用下，可能發生液膜被拉斷的行為。

2)隨著水滴直徑以及撞擊速度的增大，水滴的鋪展速度、最大鋪展半徑、最大鋪展系數均增大。水滴直徑增大時，水滴達到最大鋪展所用的時間變長，所用的無量綱時間呈微弱增大趨勢;同一直徑水滴初始速度增大時，水滴達到最大鋪展所用的時間減少，所用的無量綱時間變化相對較小。

3)低速情況下水滴撞擊光滑壁面不易發生飛濺現象，但在水滴高速撞擊光滑壁面的大韋伯數情況下，數值模擬發現了明顯的飛濺現象。

致謝:數值計算分析過程中得到了上海交通大學機械與動力工程學院工程熱物理研究所陳勇老師的支持和幫助，這里對其幫助表示感謝。

［1］Wright W B.Further refinement of the LEWICE SLD model.AIAA 2006-0464［R］.Reston:AIAA，2006.

［2］Honsek R，Habashi W G，Aube M S.Eulerian modeling of in-flight icing due to supercooled large droplets［J］.Journal of Aircraft，2008，45(4):1290-1296.

［3］Rothmayer A P，Hu H.Solutions for two-dimensional instabilities of ice surfaces uniformly wetted by thin films.AIAA 2012-3133［R］.Reston:AIAA，2012.

［4］Zhang K，Blake J，Rothmayer A，et al.An experimental investigation on wind-driven rivulet/film flows over a NACA0012 airfoil by using digital image projection technique.AIAA 2014-0741［R］.Reston:AIAA，2014.

［5］Dong W，Zheng M，Zhu J，et al.Calculation and analysis of water film flow characteristics on anti-icing airfoil surface.AIAA 2015-0538［R］.Reston:AIAA，2015.

［6］Reulet P，Aupoix B，Donjat D，et al.Boundary layer and heat transfer characterization on a flat plate with realistic ice roughness［R］.SAE Technical 2015-01-2096.

［7］易賢.飛機積冰的數值計算與積冰試驗相似準則研究［D］.綿陽:中國空氣動力研究與發展中心，2007.

［8］Dong W，Zhu J，Zhou Z，et al.Heat transfer and temperature analysis of an aero-engine strut under icing conditions［J］.Journal of Aircraft，2014，52(1):216-225.

［9］Wright W B，Potapczuk M G.Semi-empirical modeling of SLD physics.AIAA 2004-412［R］.Reston:AIAA，2004.

［10］Rutkowski A，W right W，Potapczuk M.Numerical study of droplet splashing and re-impingement.AIAA 2003-388［R］.Reston: AIAA，2003.

［11］Thoroddsen S T，Etoh T G，Takehara K.High speed imaging of drops and bubbles［J］.Annual Review of Fluid Mechanics，2008，40:257-285.

［12］Yarin A L.Drop impact dynamics:Splashing，Spreading，Receding，Bouncing［J］.Annual Review of Fluid Mechanics，2006，38(1):159.

［13］Rioboo R，Marengo M，Tropea C.Time evolution of liquid drop impact onto solid，dry surfaces［J］.Experiments in Fluids，2002，33(1):112-124.

［14］Pan K，Tseng K，Wang C.Breakup of a droplet at high velocity impacting a solid surface［J］.Experiments in Fluids，2010，48 (1):143-156.

［15］Tsai P，Pacheco S，Pirat C，et al.Drop impact upon micro-and nanostructured superhydrophobic surfaces［J］.Langmuir，2009，25 (20):12293-12298.

［16］Naber J，Reitz R.Modeling engine spray/wall impingement［J］.SAE transactions，1989，97(6):118-140.

［17］Rioboo R，Tropea C，Marango M.Outcomes from a drop impact on solid surfaces［J］.Atomization Sprays，2001，11(2):156-165.

［18］Cossali G E，Coghe A，Marengo M.The impact of a single drop on a wetted solid surface［J］.Exp.in Fluids，1997，22(6):463-472.

［19］Cossali G E，Marengo M，Coghe A.The role of time in single drop splash on thin film［J］.Experiments in Fluids，2004，36(6):888-900.

［20］Pan K L，Law C K.Dynamics of droplet-film collision［J］.Fluid Mesh.，2007，587(587):1-22.

［21］Pan K L，Cheng K R，Chou P C，et al.Collision dynamics of highspeed droplets upon layers of variable thickness［J］.Experiments in Fluids，2008，45(3):435-446.

［22］Gunjal P R，Ranade V V，Chaudhari R V.Dynamics of drop impact on solid surface:experiments and VOF simulations［J］.AIChE Journal，2005，51(1):59-78.

［23］Kim E，Baek J.Numerical study of the parameters governing the impact dynamics of yield-stress fluid droplets on a solid surface［J］.Journal of Non-Newtonian Fluid Mechanics，2012，173-174:62-71.

［24］Bussmann M，Mostaghimi J，Chandra S.On a three-dimensional volume tracking model of droplet impact［J］.Physics of Fluids，1999，11(6):1406-1417.

［25］Liang C.Numerical research on dynamic characteristics of micro droplet impact on surface and liquid film［D］.Chongqing: Chongqing University，2013.(in Chinese)梁超.微小液滴撞擊固體壁面及薄液膜動態特性的數值研究［D］.重慶:重慶大學，2013.

［26］Jia Xiaojuan.Numerical investigation on flow performance of droplet impinge upon aliquid film［D］.Dalian:Dalian University of Technology，2012.(in Chinese)賈小娟.液滴撞擊液膜流動特性數值研究［D］.大連:大連理工大學，2012.

［27］Burtnett E N.Volume of fluid simulations for droplet impact on dry and wetted hydrophobic and superhydrophobic surfaces［D］.Mississippi State:Mississippi State University，2012.

［28］Tan S C，Papadakis M.Droplet breakup，splashing and reimpingement on an iced airfoil.AIAA 2005-5185［R］.Reston: AIAA，2005.

［29］Gopala V R，Wachem B G M.Volume of fluid methods for immiscible-fluid and free-surface flows［J］.Chemical Engineering Journal，2008，141(1-3):204-221.

［30］Hirt C W，Nichols B D.Volume of fluid(VOF)method for the dynamic of free boundaries［J］.Comp.Physics，1981，39(81): 201-225.

［31］Mao T，Kuhn D C S，Tran H.Spread and rebound of liquid droplets upon impact on flat surfaces［J］.Aiche.Journal，1997，43(9):2169-2179.

Numerical investigation on dynam ic characteristics of large drop let im pacting on surface

Guo Yuxiang，Liu Yinze，Dong Wei*，Lei Guilin，Zhu Jianjun
(School of Mechanical Engineering，Shanghai Jiao Tong University，Shanghai 200240，China)

Dynamic characteristics of large droplet impacting on surface at high velocities were simulated using Volume Of Fluid method(VOF).Droplet splashing was found at the spreading phase of the droplet impacting the surface at a high velocity.At the contraction phase，the phenomenon of the slow contraction，the water ring separating with the central water film，the water central film breaking into two parts and full breaking up will appear with the diameter of the droplet decreasing and the velocity of the droplet increasing.The maximum spreading diameter and the maximum spreading coefficient increase with the increasing of the droplet diameter and the droplet velocity.The dimensionless time of reaching the maximum spreading diameter increases slightly with the diameter increasing.The variation of the dimensionless time of reaching the maximum spreading diameter is small at different velocities for the same diameter droplet.

large water droplet;numerical simulation;VOF method;water droplet impingement;water film

V211.3

A

10.7638/kqdlxxb-2015.0220

0258-1825(2016)05-0573-08

2015-12-21;

2016-07-26

國家自然科學基金(11272212，11572195);國家重點基礎研究發展計劃(2015CB755800)

郭宇翔(1993-)，男，湖北襄陽人，碩士研究生，研究方向:飛機及發動機結冰與防冰.E-mail:guoyuxiang@sjtu.edu.cn

董威*(1970-)，男，教授，博士生導師，研究方向:飛機及發動機結冰與防冰.E-mail:wdong@sjtu.edu.cn

郭宇翔，劉蔭澤，董威，等.大水滴撞擊壁面的動態特性數值模擬［J］.空氣動力學學報，2016，34(5):573-580.

10.7638/kqdlxxb-2015.0220 Guo Y X，Liu Y Z，Dong W，et al.Numerical investigation on dynamic characteristics of large droplet impacting on surface［J］.Acta Aerodynamica Sinica，2016，34(5):573-580.