三維可壓縮Navier-Stokes方程的間斷Galerkin有限元方法研究

秦望龍，呂宏強，*，伍貽兆，陳正武

(1.南京航空航天大學航空宇航學院，江蘇南京210016;2.中國空氣動力學研究與發展中心，四川綿陽621000)

三維可壓縮Navier-Stokes方程的間斷Galerkin有限元方法研究

秦望龍1，呂宏強1，*，伍貽兆1，陳正武2

(1.南京航空航天大學航空宇航學院，江蘇南京210016;2.中國空氣動力學研究與發展中心，四川綿陽621000)

拓展了二維間斷Galerkin(DG)有限元方法研究，將該數值方法用于三維可壓縮歐拉方程和Navier-Stokes方程的求解。基于六面體網格單元，采用插值方法將物面的四邊形面網格單元構造為彎曲面網格單元，更好地表述了真實物面特征;物面邊界相鄰體網格單元相應構造為高階體網格單元，其余體網格單元采用八節點六面體單元，以較小的計算代價使網格滿足DG方法計算需求。通過對三維帶bump管道內流、圓球繞流以及旋轉流線體繞流進行的數值求解，驗證了邊界彎曲方法的可行性及DG方法的高精度特性。此外，由于采用了隱式計算方法，僅需較少的時間步就能迭代收斂。

間斷有限元;Navier-Stokes方程;高精度;隱式方法;邊界彎曲

0 引言

近年來，隨著科研工作者對計算精度的要求越來越高，高精度數值方法受到越來越多的關注。在眾多的高精度方法中，間斷有限元方法由于精度高且插值模板小，易于實現網格和階數自適應，以及并行計算效率高等優點，在計算流體力學、計算聲學、計算電磁學領域都得到了廣泛的關注和發展［1］。

間斷有限元方法發展于20世紀70年代，由Reed和Hill在其解決中子運輸方程的論文中提出。20世紀80年代后期和90年代，Cockburn和Shu等人［2-5］發展了Runge-Kutta Discontinuous Galerkin (RKDG)方法，求解了非線性一維守恒律方程和方程組、高維守恒律方程和方程組，并給出了部分收斂性理論證明后，該方法才引起了人們注意，并開始逐漸應用于計算流體力學領域。目前DG方法不僅應用于雙曲守恒律方程，還被廣泛應用于求解橢圓型方程、對流擴散方程、KdV方程、Maxwell方程、可壓縮Navier-Stokes(N-S)方程等［6-18］。Bassi等［6-8］采用DG方法結合k-ω兩方程湍流模型求解了雷諾平均N-S方程，Luo等［10-12］研究了基于加權本質無振蕩(Weighted Essentially Non-Oscillatory，WENO)的重構間斷有限元方法，邱建賢等［13］針對WENO限制器在DG方法中的應用展開大量研究;張來平等［14］發展了靜動態混合重構的DG/FV混合格式。

間斷Galerkin(DG)方法通過提高單元階數來提高精度，可以在相對稀疏的網格單元上得到較高精度的數值解。但較稀疏的物面單元使得邊界表述不夠準確，從而引入額外的數值熵增［6］，使得計算結果不準確。為了對邊界進行高階表述，文獻［6，15］采用高階等參單元對二維和三維Euler方程進行了數值求解，文獻［16-17］則借助于CAD工具對全場計算單元進行了高階表述。為了減少計算代價，文獻［18-21］采用一種邊界彎曲方法在較稀疏的二維網格上得到了高精度的數值解。

本文作為二維DG方法研究［22-23］的拓展，將DG方法用于求解三維可壓縮氣動方程組。與以往工作不同點在于:將邊界網格彎曲方法拓展到三維六面體網格單元，根據四邊形面網格單元信息構造出相應的彎曲邊界信息，更準確地表述了真實壁面特征，從而在相對稀疏的網格上求解氣動方程組。為了提高DG方法的計算效率，文中采用了隱式計算方法。此外，文中發展的間斷有限元方法理論上可以拓展到任意高階精度。

1 控制方程

守恒形式的Navier-Stokes方程可以表示為

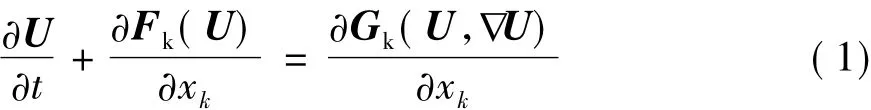
其中守恒變量U、對流通量F、黏性通量G可用下面的張量形式來表示:

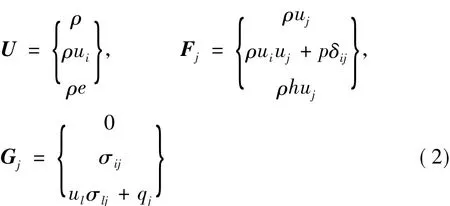
其中ρ、p、e、h分別是流體密度、壓強、單位總能和單位總焓。ui=(u，v，w)是三維笛卡爾坐標系下的速度分量，σij是黏性應力分量，qj是熱通量分量。若不考慮黏性通量G，則方程(1)退化為守恒形式的歐拉方程［12］。

2 數值方法

2.1 空間離散

令Ω表示對計算區域的一個剖分，e為剖分單元體，文中為六面體單元，?Ωe表示單元e的邊界，ne表示單元邊界?Ωe的外法矢。在方程(1)兩邊同乘測試函數ω，在計算域積分后可得:

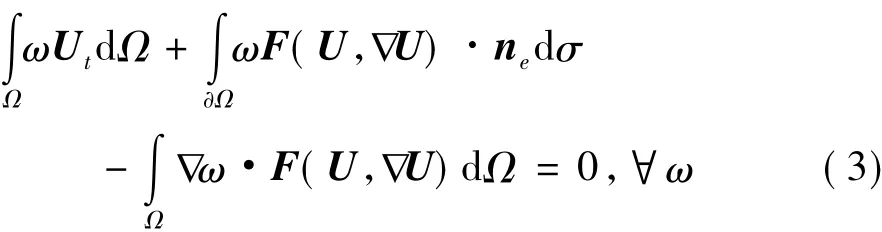
其中Pk(e)表示單元e上定義的至多k次多項式。求解方程(1)的半離散間斷有限元方法即為:求解Uh∈Vh，使得對于任意單元和任意測試函數ωh∈Vh，有:

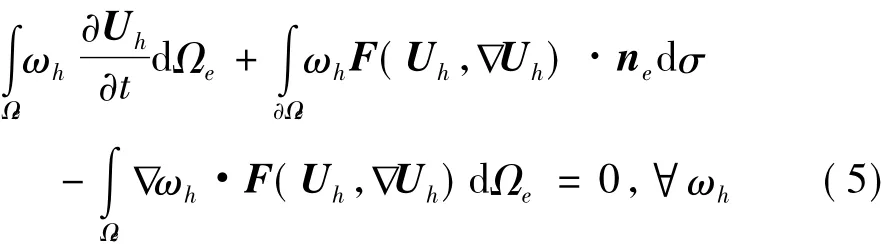
方程(5)中存在二階偏導數項，這里采用混合方法進行求解，將變量梯度看作額外變量，引入輔助變量Θ =U，得到如下方程組:

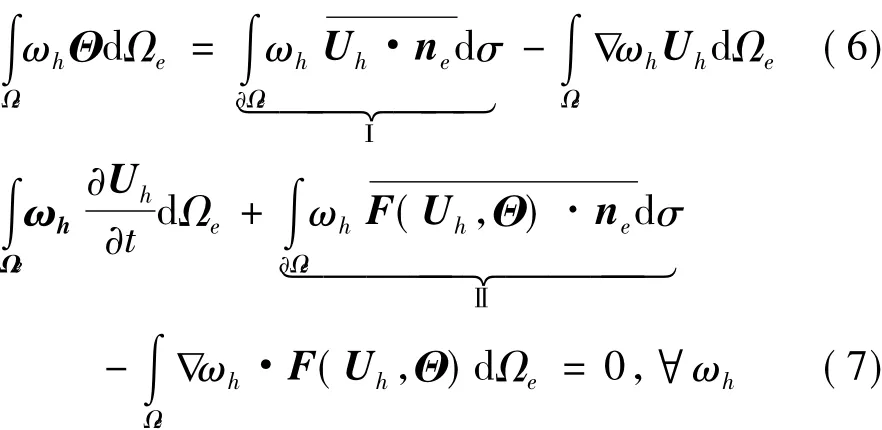
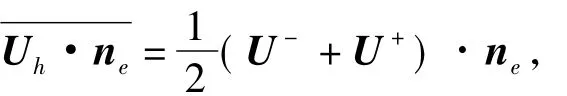
從式(8)可以看出，輔助變量可以看成單元梯度解和修正量R的和:

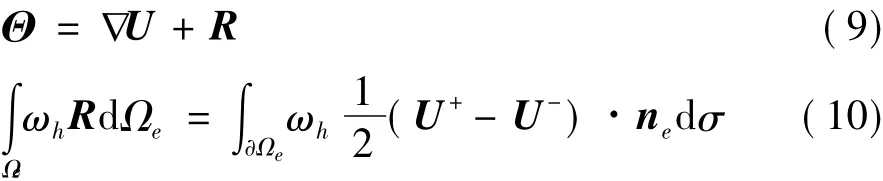
面的梯度修正量re可以表述為:

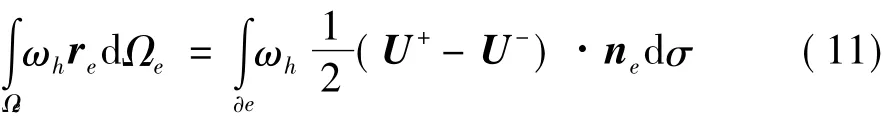
方程右邊表示在單元某個面上進行面積分，可以看出;

采用以上方法求出方程(6)中的輔助變量，方程(7)中未知量僅剩下單元變量U為未知量。數值通量II中通量函數包含無黏數值通量Hc和黏性數值通量Hv。文中無黏數值通量Hc采用LLF數值通量函數［24］，黏性數值通量Hv則取左右單元的通量平均值。

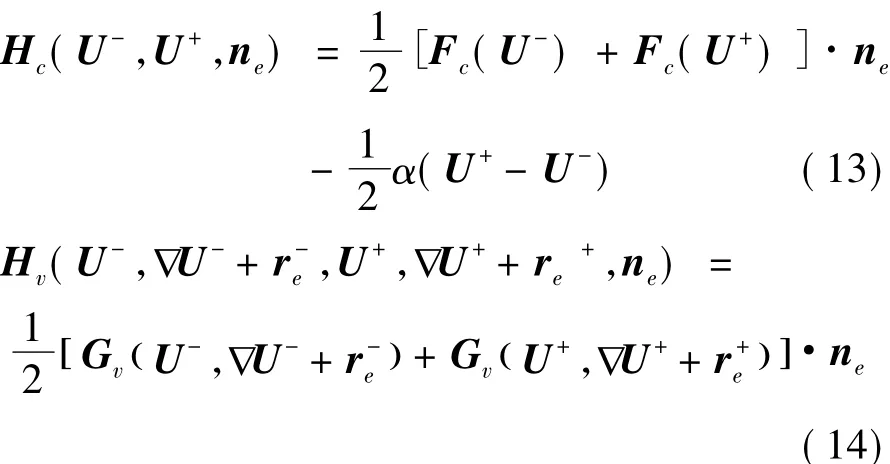
2.2 隱式時間離散

式(7)的半離散系統可以寫成常微分方程組:

M是塊對角矩陣，R(u)是總殘值，u是待求未知變量。采用牛頓方法進行線化，得到:

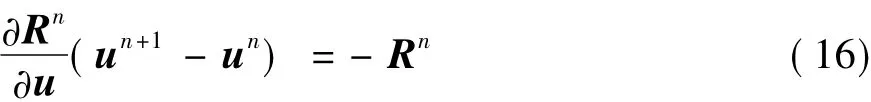
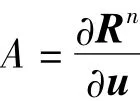
采用塊高斯賽德爾方法(BGS)方法對方程(17)進行求解:

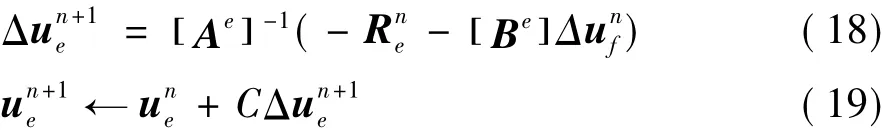
其中，［Ae］表示單元e的對角塊矩陣，［Be］表示非對角塊矩陣，表示與單元e相鄰的每個單元f在本時間步的值。式(19)中，C∈［0，1］為穩定因子，文中統一取0.5。

3 物面處理方法

3.1 彎曲物面構造方法

與二維物面彎曲構造的方法相似［22］，將三維物面邊界的四邊形單元從計算空間(x，y，z)轉換到參考空間(ξ，η，ζ)，在參考坐標平面構造曲面:

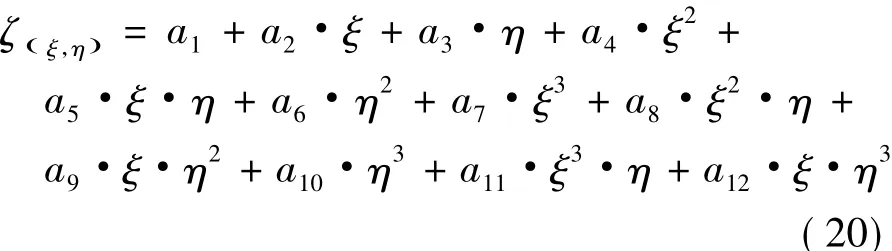
系數根據點的坐標和加權法矢信息(式21)得到。

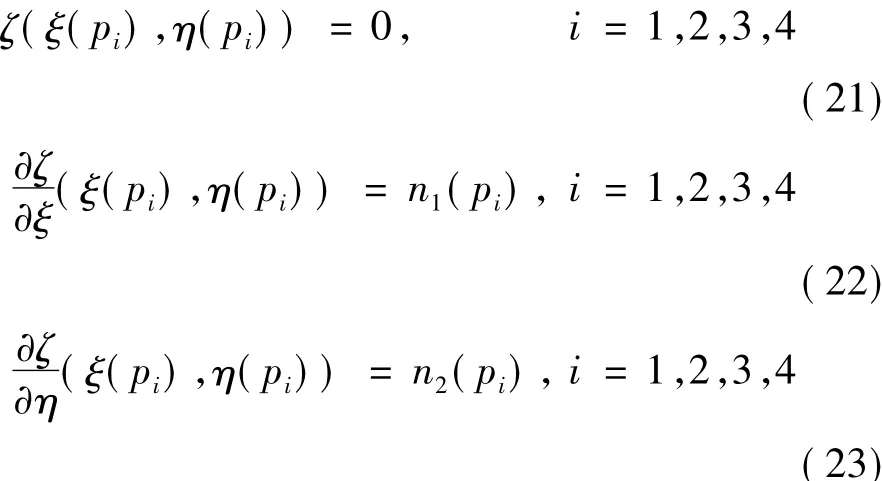
其中pi為計算空間四邊形單元的頂點，n1(pi)、n2(pi)為頂點的加權偏導數項轉換到參考平面后的數值。將參考空間構造得到的曲面映射到原(x，y，z)計算空間即得到重構的彎曲物面邊界。區別于二維曲面重構后的連續和一階導數連續的特性［18，22］，三維重構曲面僅有連續特性。具體曲面重構步驟如下:

1)在(x，y，z)計算空間根據加權方法得到四邊形頂點的偏導數項Ni，i=1，2，3。

2)假設物面四邊形的四個頂點處于同一平面，取其中三點pi(i=1，2，3)從計算空間(x，y，z)映射到(ξ，η，ζ)空間使滿足式(21)，可以得到兩個坐標空間的映射矩陣T。根據映射矩陣T，將各頂點的法矢Ni轉換到參考平面得到ni，i=1，2，3。根據ni計算得到n1(pj)和n2(pj):

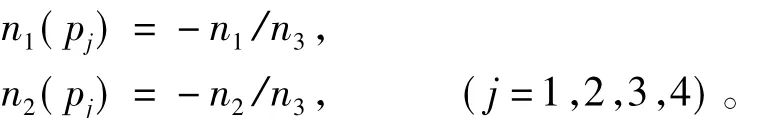
3)根據方程(21)～(23)，求出系數a1～a12。

4)將(ξ，η，ζ)空間下的曲面信息映射到原(x，y，z)計算空間，得到高階表述后的面單元(圖1)。

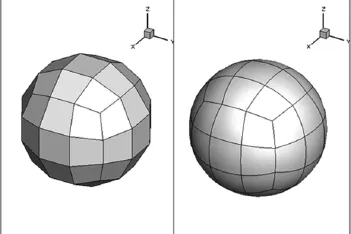
圖1 圓球的邊界彎曲示意圖Fig.1 Illustration of curved boundary representation method on a sphere

實際計算中，為了盡可能滿足步驟2中“四個頂點處于同一平面”的假設，在彎曲弧度較大的地方需要適當加密網格。

圖2給出了曲面構造后圓球Z=0截面與真實圓的誤差，圖3給出了誤差隨角度的分布情況。該算例中Z=0截面的誤差最大不足1%，實際計算中可以通過增加物面網格單元個數進一步減小曲面構造帶來的誤差。

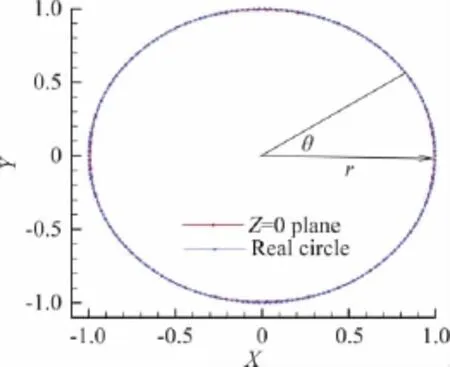
圖2 曲面重構后Z=0截面的誤差Fig.2 Illustration of the deviation on Z=0 plane

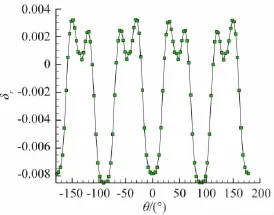
圖3 曲面重構后Z=0截面的誤差隨角度的分布Fig.3 Illustration of the deviation according to the angle on Z=0 p lane

3.2 高階單元映射

對于非物面單元，根據六面體單元的八個頂點進行線性映射:

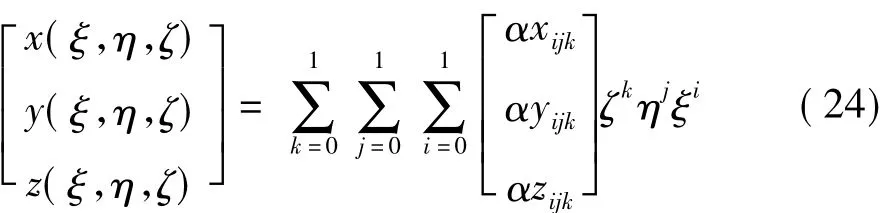
由于物面邊界進行了彎曲重構，物面體網格單元采用32點進行高階映射(圖4)。映射關系如下:

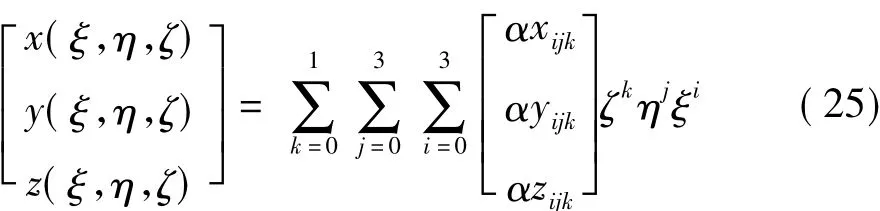
根據已有坐標信息求出未知系數αxijk、αyijk和αzijk，即可得到單元映射雅克比矩陣及其他所需的映射關系。

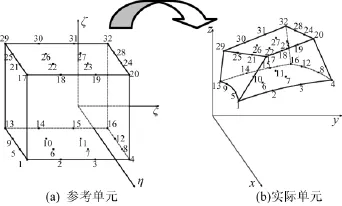
圖4 六面體單元映射點示意圖Fig.4 Illustration of mapping points for 32-node hexahedral element

4 數值結果與分析

4.1 三維含Bump管道內流

采用該內流問題驗證邊界彎曲方法對間斷有限元格式的精度影響。該算例計算區域的長度，寬度和高度分別為3、0.5、0.8。計算邊界示意圖見圖5，入口采用亞聲速來流，馬赫數M∞=0.5，出口為自由出流。兩側面和上表面為對稱邊界條件，下表面為滑移邊界。下表面Bump的表達式為z=0.0625e－25x2，x∈(－1.5，1.5)。由于該流動問題是求解歐拉方程，且幾何和流動均光滑，所以理論上流場等熵，文中采用熵增作為衡量精度的標準。

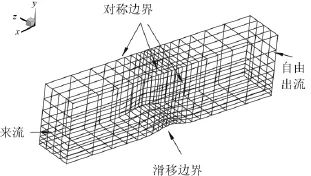
圖5 含Bum p管道內流邊界示意圖Fig.5 Illustration of boundary conditions for subsonic flow through a channel w ith a bum p on the lower surface at M∞=0.5

熵增ε的定義如下:

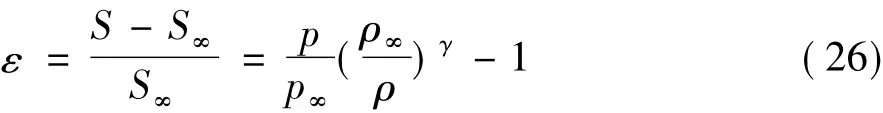
采用三套連續剖分加密的網格，網格點分布為11×5×3、21×9×5、41×17×9，單元數分別為80、640、5120，如圖6。

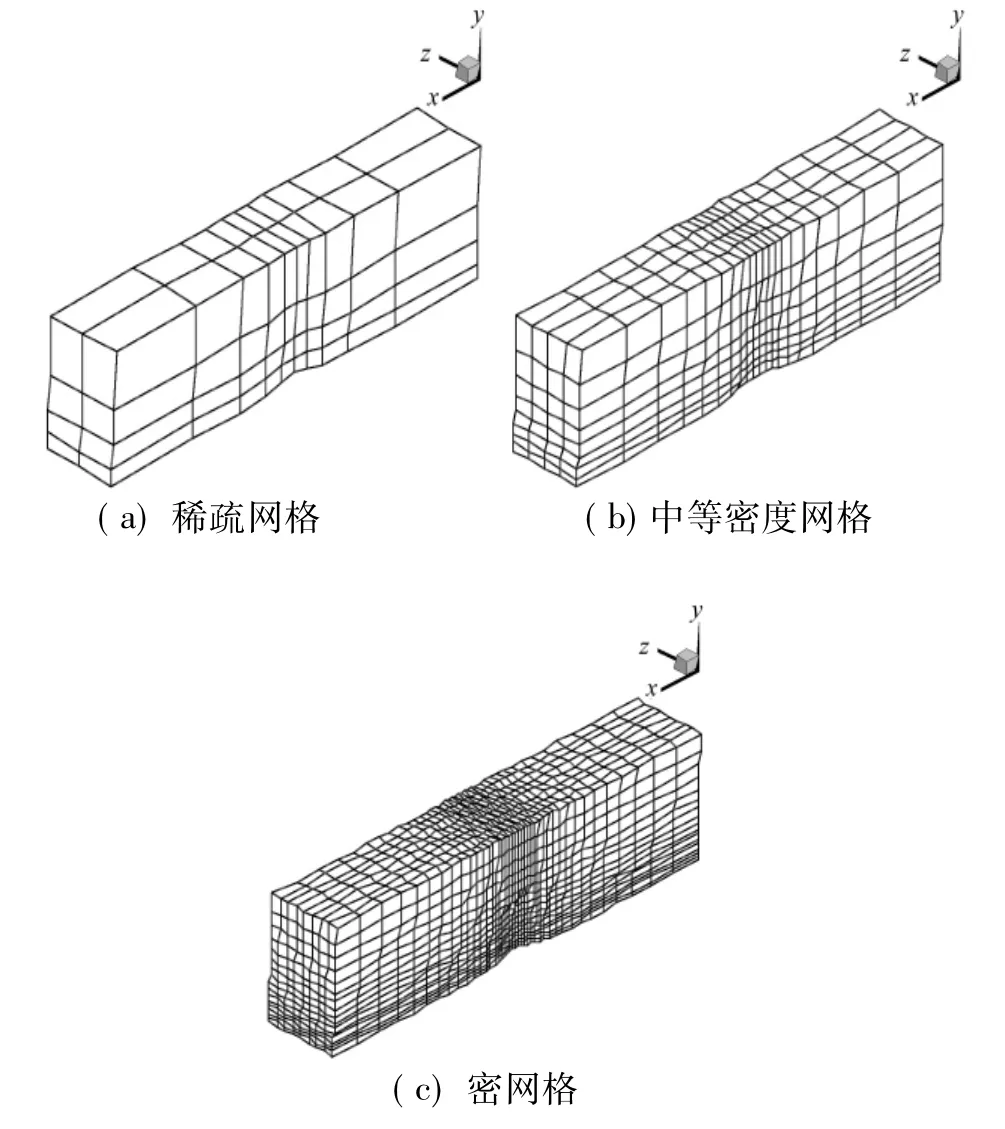
圖6含Bum p管道內流計算網格Fig.6 A sequence of three successively refined meshes used for com puting subsonic flow through a channel w ith a bump

圖7 為該算例的精度計算結果，橫坐標表示網格的尺度。比較邊界彎曲修正前后的精度曲線可知，當對彎曲幾何的表述不足時，計算得到的熵增較大，且階數較高時存在精度損失。邊界彎曲修正方法提高了該算例的幾何表述，從而空間離散達到了格式的設計精度。

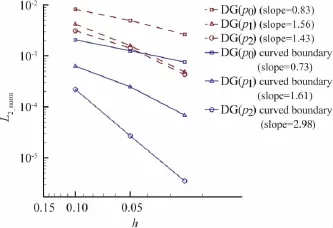
圖7三維含Bump管道內流精度測試收斂速率曲線Fig.7 Rates of convergence for subsonic flow through a channel w ith a bump

圖8 為邊界彎曲之后密網格上計算得到的三階精度(p=2)的壓力等值線圖，可以看出，流場的等值線較光滑且對稱性較好。圖9為邊界彎曲后密網格上采用隱式計算方法(p=0～2)計算收斂所需的迭代步和計算時間，由于采用前一階的計算結果作為下一階數值計算的初值，計算時間和迭代步數大幅減少，密度殘值收斂到-10量級僅需20個牛頓步。隨著階數的提高，自由度呈倍增加，計算所需的時間相應呈倍增加，在計算資源有限的情況下文中只計算到三階精度(p=2)。

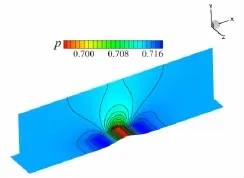
圖8 三維含Bum p管道內流壓力等值線圖Fig.8 Pressure contours for subsonic flow through a channel w ith a bump

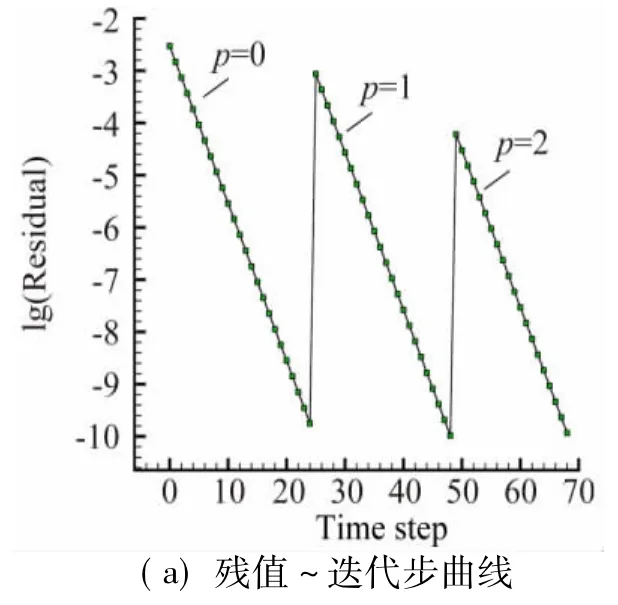
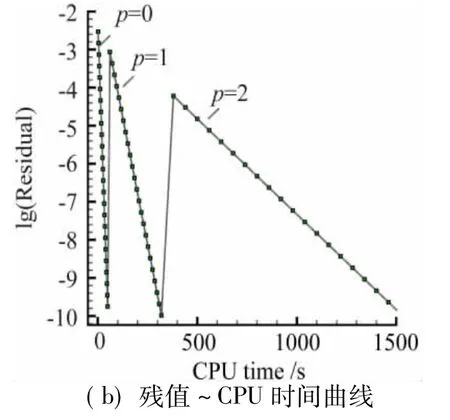
圖9 三維含Bump管道內流密度殘值收斂曲線Fig.9 Logarithm ic density residual versus time step and CPU time for subsonic flow through a channel w ith a bump

4.2 圓球黏性流動

選取低雷諾數圓球繞流算例驗證邊界彎曲方法在黏性流動中的適用性。自由來流條件為:馬赫數M∞=0.5，雷諾數Re∞=118。取半模進行數值計算，網格單元總數為9300，物面單元總數為192(圖10)。

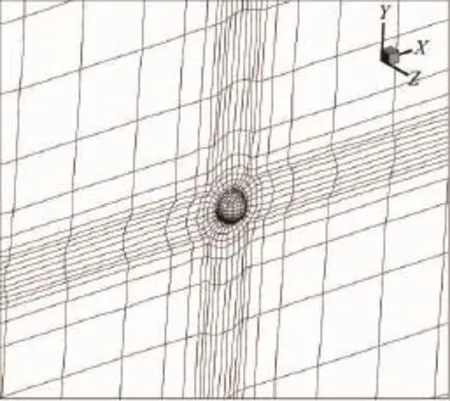
圖10圓球黏性流動計算網格Fig.10 M esh used for computing lam inar flow past a sphere

圖11 為壁面彎曲前后三階精度(p=2)下計算得到的球表面及Z=0對稱面的壓力等值線圖。可以看出，準確的壁面表述對DG方法較為重要，壁面彎曲后計算得到的等值線較為光滑和對稱。圖12為計算得到的Z=0對稱面的壓力系數曲線，經過壁面彎曲修正后得到的壓力系數曲線較為光滑連續。

圖13為壁面彎曲前后三階精度(p=2)的密度殘值下降曲線。可以看出，物面彎曲對隱式方法的收斂效率同樣有較大影響。

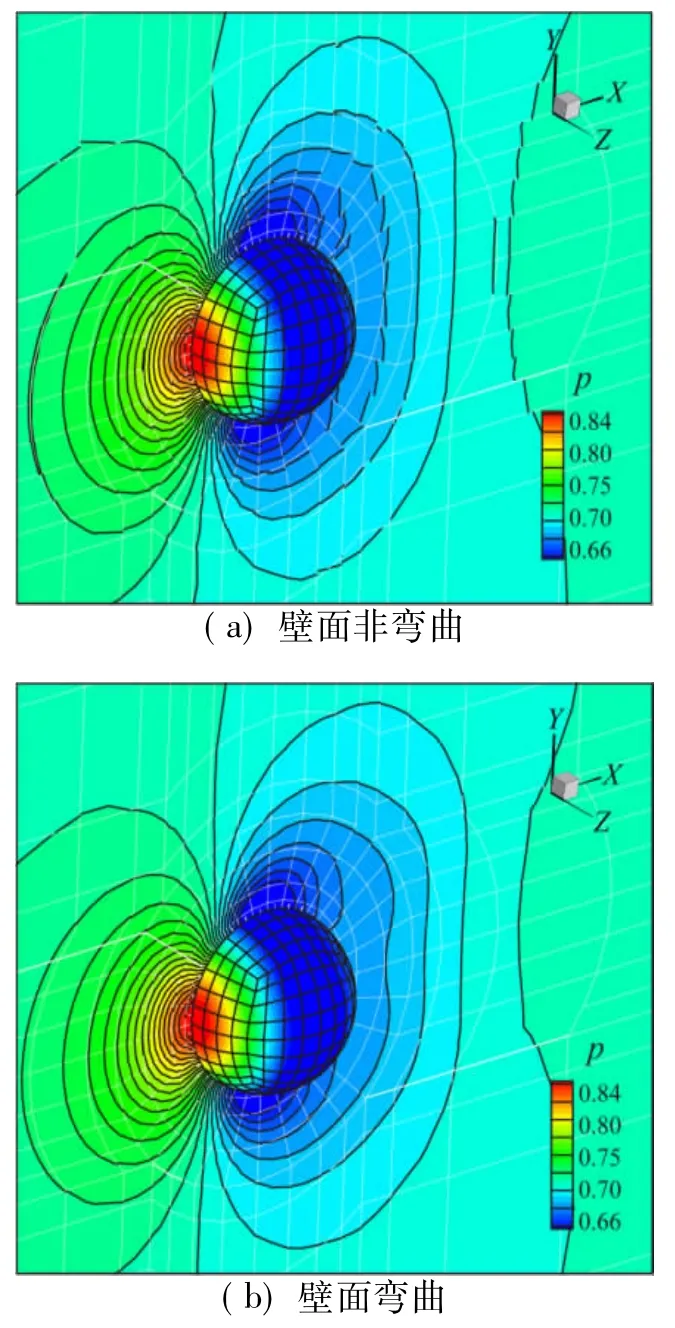
圖11 圓球黏性流動壓力等值線Fig.11 Com puted pressure contours in the flow field

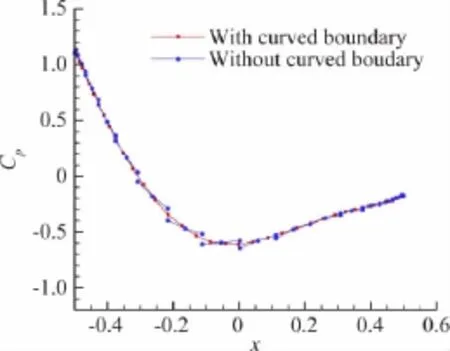
圖12 圓球黏性流動Z=0截面計算壓力系數曲線比較Fig.12 Comparison of computed pressure coefficient on Z=0 plane

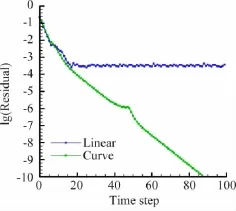
圖13 三維圓球黏性流動密度殘值收斂曲線Fig.13 Logarithm ic density residual versus time step for flow past a sphere

4.3 旋轉流線體繞流

選取High-order CFD Workshop［25］的三維旋轉流線體層流算例驗證文中的邊界彎曲方法對于較復雜曲面的適用性。計算自由來流條件為:馬赫數M∞= 0.5，雷諾數Re∞=5000，迎角α=1°。計算網格單元總數為18294，物面單元總數為582(圖14)，在物面前緣和后緣進行網格局部加密。圖15和圖16分別給出了三階精度(p=2)的計算等密度線圖和等馬赫線圖，即使物面網格相對稀疏，采用邊界彎曲方法后得到的結果依然較為光滑。圖17為本算例的密度殘值收斂曲線，由于采用了高效的隱式計算方法，殘值在30個牛頓步內均收斂到-6量級以下。

圖14 旋轉流線體黏性流動計算網格Fig.14 M esh used for computing lam inar flow past a stream lined body

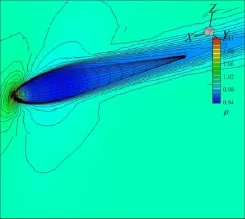
圖15 旋轉流線體黏性流動密度等值線圖Fig.15 Density contours for lam inar flow past a stream lined body

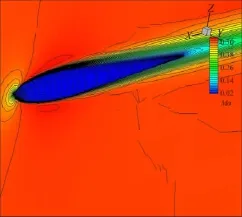
圖16 旋轉流線體黏性流動馬赫數等值線圖Fig.16 M ach number contours for lam inar flow past a stream lined body

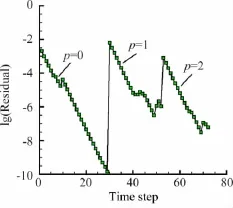
圖17 三維旋轉流線體黏性流動密度殘值收斂曲線Fig.17 Logarithm ic density residual versus time step for lam inar flow past astream lined body

5 結論

本文將間斷有限元方法拓展到三維可壓縮氣動方程組的求解中。與以往一些數值方法的區別在于:在三維情況下對邊界四邊形網格單元進行了彎曲重構，更準確地表述了物面特征，從而使得DG方法在相對稀疏的網格上就能得到高精度的數值解。同時采用了魯棒可靠的隱式方法，縮短了計算時間，提高了計算效率。對Euler方程和Navier-Stokes方程數值求解的結果表明，文中的壁面彎曲方法能較好地應用于間斷有限元方法且有很好的魯棒性。后續將設計高效的并行算法進一步提高計算效率，同時考慮加入湍流模型研究更復雜的流動問題。

［1］Wang Z J.High-order methods for the Euler and Navier-Stokes equations on unstructured grids［J］.Progress in Aerospace Sciences，2007，43(1):1-41.

［2］Cockburn B，Shu C W.The Runge-Kutta discontinuous Galerkin method for conservation laws V:multidimensional systems［J］.Journal of Computational Physics，1998，141(2):199-224.

［3］Cockburn B，Shu C W.The local discontinuous Galerkin method for time-dependent convection-diffusion systems［J］.SIAM Journal on Numerical Analysis，1998，35(6):2440-2463.

［4］Cockburn B，Shu C W.Runge-Kutta discontinuous Galerkin methods for convection-dominated problems［J］.Journal of scientific computing，2001，16(3):173-261.

［5］Cockburn B，Li F，Shu C W.Locally divergence-free discontinuous Galerkin methods for the Maxwell equations［J］.Journal of Computational Physics，2004，194(2):588-610.

［6］Bassi F，Rebay S.High-order accurate discontinuous discontinuous finite element solution of the 2D Euler equations［J］.Journal of Computational Physics，1997，138(2):251-285.

［7］Bassi F，Rebay S.A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations［J］.Journal of Computational Physics，1997，131(2):267-279.

［8］Bassi F，Crivellini A，Rebay S，et al.Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k-ω turbulence model equations［J］.Computers＆Fluids，2005，34(2):507-540.

［9］Lyu Hongqiang，Sun qiang，Qin Wanglong.3D numerical solution of aero-noise with high-order discontinuous Galerkin method［J］.Journal of Nanjing University of Aeronautics＆Astronautics，2013，30(3):227-231.

［10］Xia Y，Luo H，Nourgaliev R.An implicit Hermite WENO reconstruction-based discontinuous Galerkin method on tetrahedral grids［J］.Computers＆Fluids，2014，96:406-421.

［11］Luo H，Xia Y，Li S，et al.A Hermite WENO reconstruction-based discontinuous Galerkin method for the Euler equations on tetrahedral grids［J］.Journal of Computational Physics，2012，231(16): 5489-5503.

［12］Luo H，Luo Luqing，Nourgaliev R，et al.A reconstructed discontinuous Galerkin method for the compressible Navier-Stokes equations on arbitrary grids［J］.Journal of Computational Physics，2010，229(2):6961-6978

［13］Zhu J，Qiu J.WENO Schemes and their application as limiters for RKDG methods based on trigonometric approximation spaces［J］.Journal of Scientific Computing，2012:1-39.

［14］Zhang Laiping，Li Ming，Liu Wei，et al.Recent development of high order DG/FV hybrid methods［J］.Acta Aerodynamica Sinica，2014，32(6):717-726.(in Chinese)張來平，李明，劉偉，等.基于非結構/混合網格的高階精度DG/FV混合方法研究進展［J］.空氣動力學學報，2014，32 (6):717-726.

［15］Li S.A parallel discontinuous Galerkin method with physical orthogonal basis on curved elements［J］.Procedia Engineering，2013，61:144-151.

［16］Wang L，Anderson W K，Erwin J T，et al.Solutions of high-order methods for three-dimensional compressible viscous flows［C］// 42nd AIAA Fluid Dynamics Conference and Exhibit.New Orleans，2012.

［17］Hartmann R，Held J，Leicht T，et al.Discontinuous Galerkin methods for computational aerodynamics—3D adaptive flow simulation with the DLR PADGE code［J］.Aerospace Science and Technology，2010，14(7):512-519

［18］Landmann B，Kessler M，Wagner S，et al.A parallel，high-order discontinuous Galerkin codes for laminar and turbulent flows［J］.Computers＆Fluids，2008，37(2):427-438.

［19］Lübon C，Ke?ler M，Wagner S.A parallel CFD solver using the discontinuous Galerkin approach［M］//High Performance Computing in Science and Engineering，Garching/Munich 2007.Springer Berlin Heidelberg，2009:291-302.

［20］Yu Jian，Yan Chao.Discontinuous Galerkin method based on artificial viscosity［J］.Acta Aerodynamica Sinica，2013，31(3): 371-375.(in Chinese)于劍，閻超.基于人工粘性的間斷Galerkin有限元方法［J］.空氣動力學學報，2013，31(3):371-375.

［21］Xia Yidong，Wu Yizhao，Lyu Hongqiang，et al.Parallel computation of a high-order discontinuous Galerkin method on unstructured grids［J］.Acta Aerodynamica Sinica，2011，29(5): 537-541.(in Chinese)夏軼棟，伍貽兆，呂宏強，等.高階間斷有限元法的并行計算研究［J］.空氣動力學學報，2011，29(5):537-541.

［22］Qin Wanglong，Lyu Hongqiang，Wu Yizhao.High-order discontinuous Galerkin solution of N-S equations on hybrid mesh［J］.Chinese Journal of Theoretical and Applied Mechani，2013，45(6):987-991.(in Chinese)秦望龍，呂宏強，伍貽兆.基于混合網格的高階間斷有限元黏流數值解法［J］.力學學報，2013，45(6):987-991.

［23］Qin Wanglong，Lyu Hongqiang，Wu Yizhao.Discontinuous Galerkin solution of RANS equations on curved mesh［J］.Acta Aerodynamica Sinica，2014，32(5):581-586.(in Chinese)秦望龍，呂宏強，伍貽兆.彎曲網格上的間斷有限元湍流數值解法研究［J］.空氣動力學學報，2014，32(5):581-586.

［24］Toro E F，Spruce M，SpearesW.Restoration of the contact surface in the HLL-Riemann solver［J］.Shock Waves，1994，4(2):25-34.

［25］High-order CFD Workshop.Problem C 2.3.Analytical 3D Body of Revolution［OL/EB］.http://www.as.dlr.de/hiocfd/case_c2.3.html

Discontinuous Galerkin method for 3-D com pressible Navier-Stokes equations

Qin Wanglong1，Lyu Hongqiang1，*，Wu Yizhao1，Cheng Zhengwu2
(1.College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China;2.China Aerodynamics Research and Development Center，Mianyang 621000，China)

A curved-boundary based discontinuous Galerkin(DG)method is developed for solving three-dimensional compressible Euler and N-S equations on hexahedral grids.In this method，the quadrilateral face elements are reconstructed to be curved with polynomial interpolation approach，which is better to represent the real boundary.With high-order volume elements clustering only around the boundary surface，this method is easy to implement and requires a small amount of extra computations.Numerical experiments on a variety of flow problems demonstrate that DG method can obtain high-order accurate solutions on relatively coarse grids with the presented curved boundary representation approach.It is worth noting that with an implicit time integration method，converging solutions can be achieved within several time steps.

discontinuous Galerkin method;Navier-Stokes equations;high-order method;implicit method;curved boundary

V211.3

Adoi:10.7638/kqdlxxb-2015.0060

0258-1825(2016)05-0617-08

2015-05-08;

2015-09-09

國家自然科學基金(11272152);航空基金(20152752033);氣動噪聲控制重點實驗室開放課題;江蘇高校優勢學科建設工程資助項目

秦望龍(1988-)，男，江蘇南京，博士研究生，研究方向:計算流體力學，間斷有限元方法.E-mail:qinwanglong@126.com

呂宏強*，博士，教授.E-mail:hongqiang.lu@nuaa.edu.cn

秦望龍，呂宏強，伍貽兆.三維可壓縮Navier-Stokes方程的間斷Galerkin有限元方法研究［J］.空氣動力學學報，2016，34(5): 617-624.

10.7638/kqdlxxb-2015.0060 Qin W L，Lyu H Q，Wu Y Z.Discontinuous Galerkin method for 3-D compressible Navier-Stokes equations［J］.Acta Aerodynamica Sinica，2016，34(5):617-624.