一種相似性框架下基于非線性擴散過程的剩余壽命估計模型

裴洪，胡昌華，王兆強，張正新，張會會

(火箭軍工程大學302室，陜西西安710025)

一種相似性框架下基于非線性擴散過程的剩余壽命估計模型

裴洪，胡昌華，王兆強，張正新，張會會

(火箭軍工程大學302室，陜西西安710025)

剩余壽命(residual life，RL)估計是預測與健康管理(prognostics and health management，PHM)的關鍵環節。目前，傳統的基于相似性的RL估計模型僅利用失效設備的退化數據，忽略截斷設備和運行設備的退化數據，難以保證RL的估計精度。針對該問題，在相似性框架下提出一種新的基于擴散過程的RL估計模型。首先基于擴散過程對截斷設備進行退化建模和RL估計，然后通過比較參考設備(失效設備與截斷設備)和運行設備間的相似性，同時利用參考設備與運行設備的退化數據實現運行設備的RL估計。最后仿真實驗驗證該文模型優于傳統的基于相似性的模型。研究結果表明:該文模型能夠顯著提高運行設備RL的估計精度，具有潛在的工程應用價值。

剩余壽命;擴散過程;相似性;參考設備

0 引言

隨著對工程設備安全性和可靠性要求的不斷提高，預測與健康管理(PHM)技術受到了學術界和工業界的普遍關注［1］。作為一種新興技術，PHM能夠提高設備的可靠性和安全性、降低失效事件發生的概率，對于航空航天、武器裝備及工業制造等領域至關重要［2，3］。作為PHM的重要環節，剩余壽命(RL)估計可為PHM技術中決策活動(如最優維護、備件訂購等)的有效開展提供前提和基礎。因而，近年來RL估計成為當前研究中的熱點問題，并涌現出了大量的研究成果［4－6］。

現有的RL估計方法主要可以分為失效物理分析和數據驅動2類方法［1］。失效物理分析方法通過事先獲取設備的物理失效機制進而實現其RL估計。在實際工程中，對于大型化或復雜化設備來說，事先獲取物理失效機制的難度很大，同時對于一些價格昂貴的設備來說，物理模型的獲取成本過高［6］。隨著傳感器技術和狀態檢測技術的發展，數據驅動的方法凸顯出特有的優越性。當前數據驅動的方法大致分為傳統的RL估計方法和基于退化建模的RL估計方法。傳統的RL估計方法通過對設備的壽命數據進行分析進而確定壽命的概率分布。然而，隨著科技的進步，實際設備的壽命和可靠性不斷提高，通常難以獲取足夠的壽命數據，尤其是對于一些價格昂貴的設備來說，獲取壽命數據的經濟成本過高甚至難以承受，這使得傳統的RL方法在實際中常常難以適用。基于退化數據的方法不僅能夠降低實驗成本，而且能夠提高RL估計的精度，已成為目前的主流方法［4］。事實上，不僅可以從總體中獲得失效設備或截斷設備的退化數據，而且可以獲得運行設備自身的退化數據。如何有效地利用這些數據實現設備RL的估計是當前研究的重點［1－8］。

由于設備內部結構和使命任務的相似性，同類設備間的退化過程或退化數據必然具有某種相似性。近年來，考慮同類設備間相似性的退化建模和RL估計方法，即基于相似性的方法，已逐步引起了國內外學者的關注，并取得了較好的實際應用效果。Wang等［9］針對失效設備足夠多的情況通過構建退化數據庫，提出了一種基于相似性的RL估計的方法。Zio等［10］基于相似性方法采用隸屬度函數衡量設備間相似度，進而確定RL估計值。文獻［11］基于在不同監測點運行設備與參考設備間相似性所占權重具有差異性，提出一種廣義的相似性模型進行RL估計，進一步推廣了基于相似性的方法，提高了RL估計精度。文獻［12］在相似性的框架下，利用失效設備的退化數據主要研究了權重函數對估計精度的影響、RL估計的魯棒性以及RL估計的不確定性。然而，上述方法均忽略了截斷設備的退化數據和運行設備的自身退化數據，在一定程度上無法保證RL估計精度。You等［13］在相似性框架下利用失效設備和截斷設備的退化數據對RL進行估計，然而該方法采用傳統相似性方法對截斷設備的RL進行估計，并且將截斷設備看成失效設備，具有一定的局限性。鑒于此，本文在相似性框架下提出一種基于非線性擴散過程的RL估計方法。利用參考設備的退化數據和運行設備的退化數據，通過比較參考設備與運行設備間的相似性確定參考設備的權重，與文獻［13］的不同在于基于擴散過程模型確定截斷設備的RL，進而實現運行設備的RL估計。數值仿真驗證了本文模型能夠提高RL的估計精度。

1 問題描述

基于相似性的RL估計方法主要通過分析失效設備與截斷設備的RL權重，進而實現運行設備的RL估計。基于相似性的RL估計方法的關鍵要素如圖1所示。其中，D表示運行設備和參考設備間相似性測量的時間范圍，s(·)為測量兩種設備之間相似性的測度函數，如概率或歐式距離［9］，表示在第k個狀態監測點運行設備與第i個參考設備間的相似性。權重函數w(·)根據不同參考設備與運行設備間的相似性確定其權重，并將相似性代入權重函數中得到權重w(so?ri(k))，用wi(k)表示。PRL0(k)表示運行設備在第k個狀態監測點的RL估計值，RRLri(Ni(k))表示第i個參考設備在第k個狀態監測點的RL，Ni(k)為監測點數目。

圖1 基于相似性的RL估計方法的關鍵要素

傳統的基于相似性的方法均假定參考設備為失效設備，而工程設備的失效往往會造成人員傷亡和財產損失，故有限的失效設備限制了傳統的基于相似性方法的適用性。文獻［13］同時考慮了失效設備和截斷設備的退化數據，拓寬了參考設備的范疇，但在實際工程中，截斷設備即在實際運行過程中未發生失效的設備，因而無法預知截斷設備的實際RL，因而文獻［13］僅簡單地將截斷設備看成失效設備，仍采用傳統相似性的方法進行RL估計，難以保證估計的精度。針對該問題，本文主要考慮基于擴散過程的模型對截斷設備的RL進行估計，進而實現運行設備的RL估計。

基于以上分析，本文主要研究以下問題:

1)如何基于擴散過程模型對截斷設備的RL進行估計。

2)如何將步驟1)得到的截斷設備的RL估計結果融入相似性的框架內，利用運行設備和參考設備的退化數據提高RL估計精度。

2 相似性框架下基于擴散過程的RL估計

2.1 截斷設備的RL估計

擴散過程模型已廣泛應用于設備退化模型構建和RL估計之中［7，14］。常見的基于擴散過程的退化模型［7］可以表示為

式中:Y(t)——設備在t時刻的退化量;

y0——退化量初始值;

λ——漂移系數的尺度參數;

θ——漂移系數的形狀參數;

σB——擴散系數;

B(t)——標準布朗運動。

對于一批設備來說，由于制造工藝及運行環境的差異性，每個設備的退化路徑總會存在差異性。因而，令λ為服從正態分布的隨機參數，即，以刻畫出同類不同個體設備間的差異性［7，14］。

設備的失效時間通常定義為公式(1)所示的退化過程首達既定失效閾值ω的時間，即首達時間［14－15］。基于首達時間的概念，tk時刻的RL可以定義為，根據文獻［7］，不考慮λ的隨機性時tk時刻RL的概率密度函數(probability density function，PDF)可以表示為

可以得到隨機參數作用下RL的PDF，其中，f(λ)為隨機參數λ的PDF。

假定有N組截斷設備的歷史退化數據，對于截斷設備i(i=1，2，…，N)，在ti1，ti2，…，tini時刻，測得了設備i的ni個退化量，記作Yi=(Yi(ti1)，Yi(ti2)，…，Yi(tini))T。因而，截斷設備i的退化模型可以表示為

其中j=1，2，…，ni。令，根據文獻［7］，Yi服從多變量正態分布，其均值和協方差分別為

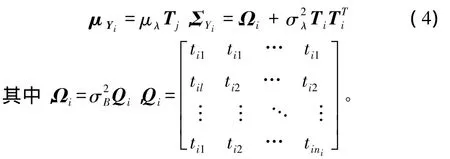
分別求似然函數對μλ和σλ的一階偏導數，可以得到如下結果:

參數估計完成后，將進行RL的PDF的推導，對于式(1)定義的非線性隨機退化過程，則tk時刻以w為閾值的RL的PDF可以表示為

對于第i臺截斷設備在tR時刻的RL的期望值可表示為，那么如何利用這類數據，即如何將擴散過程融入相似性框架中，將在下節討論。

2.2 相似性框架下運行設備的RL估計

圖2總結了相似性框架下基于擴散過程的RL估計方法。其中，Q為失效設備的數目，P為截斷設備的數目，SRL(k)為截斷設備在第k個狀態監測點的RL。A步中，利用截斷設備的退化數據，基于擴散過程方法對截斷設備的RL進行估計。B步中，利用全部退化過程，在該框架下估計運行設備第k個狀態監測點的RL。從圖2可以看出，H為非負整數并且(H+1)·Δt=D，即圖1中的時間間隔，B步中，利用連續H+1個狀態監測點測量參考設備和運行設備間的相似性。實際工程中，H或D由專家給定，根據H+1個監測點可以獲取運行設備的當前狀態，下節將深入研究H對RL估計的影響。

圖2 相似性框架下基于擴散過程的RL估計流程

令y0(k·Δt)表示運行設備第k個監測點的退化量，其中Δt為狀態監測間隔，k為正的監測數。令yri(k·Δt)表示參考設備i第k個監測點的退化量。本文選擇歐式距離函數測量運行設備和參考設備間的相似性:

式中，s(k，H，i，m)表示運行設備在［(k－H)·Δt，k·Δt］區間的退化過程與參考設備i在［(m－H)· Δt，m·Δt］區間的退化過程間的相似性，對于運行設備有k≥H+1，對于失效設備有H+1≤m≤Mi，對于截斷設備有H+1≤m≤Gi。其中，Mi表示失效設備i的監測點數目，Gi表示截斷設備i的監測點數目。根據式(7)，在第k個監測點，參考設備i與運行設備間的相似性可以表示為

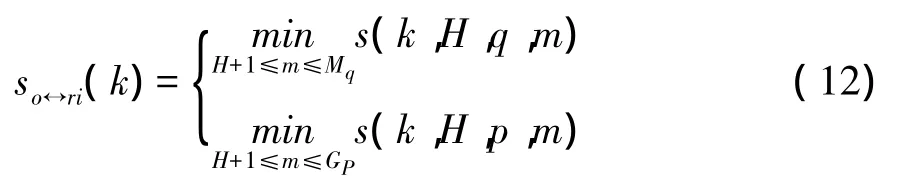
其中q，p為正整數。

在計算so?ri(k)時，Ni(k)能夠表示為

第i個參考設備在Ni(k)監測點的RL估計值可以表示為

根據文獻［11］，權重函數可定義為

其中，zi(k)定義為

式(16)中，參數α決定了分配到每臺參考設備的權重，文獻［12］研究了α對基于相似性的退化模型的影響。

根據式(15)中定義的權重和式(14)中參考設備的RL，可以得到運行設備在第k個狀態監測點的RL估計值:

通過上述分析，基于圖2中的流程框圖，運行設備RL估計的算法概括如下。

步驟1:利用截斷設備的歷史退化數據實現基于擴散過程模型的參數估計;

步驟2:基于式(14)利用步驟1的參數估計結果實現參考設備(截斷設備或失效設備)i在監測點Ni(k)的RL估計;

步驟3:基于相似性定義和式(15)，利用參考設備的全部退化數據與運行設備自身的退化數據確定每個參考設備相對于運行設備的權重wi(k);

步驟4:基于式(17)能夠確定運行設備在第k個狀態監測點的RL估計值PRL0(k)，實現運行設備RL的實時估計。

3 實驗研究

本節通過數值仿真產生10組失效設備、9組截斷設備及1組運行設備的退化數據，假定退化數據單位為mm，利用本文方法與傳統的基于相似性的方法［16］分別估計運行設備的RL，并比較本文方法與傳統的基于相似性的方法間的RL估計結果。

3.1 數值仿真

利用式(1)定義的模型產生仿真數據，參數設定如下:μλ=1，σλ=0.1，σB=1，θ=0.9，且Δt=1h。根據2.1節提到的首達時間定義，一旦退化數據超出了閾值，意味著設備發生失效，本文令ω=50 mm。圖3描繪了20組帶有失效閾值的退化過程。

根據式(1)隨機仿真得到20組超過失效閾值的退化過程，作為參考設備和運行設備的退化過程，對本文方法進行評估。由于仿真得到的數據均超出了失效閾值，故為失效設備的退化過程。為獲取截斷設備的退化過程，隨機選取9組仿真過程作進一步裁剪，裁剪后的退化過程可作為截斷設備的退化過程。隨機選取常數Tr，如Tr=60 h，并且移走Tr與失效時刻間的退化過程，即可獲取截斷設備的退化過程。根據截斷設備的數目選擇Tr，一旦Tr確定后，設備的退化過程在監測點Tr不會超出閾值。基于圖3的仿真數據，圖4給出了9組截斷設備的退化過程。

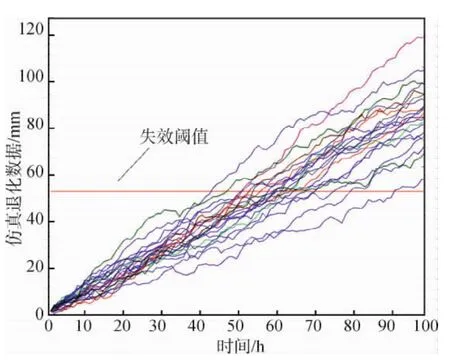
圖3 20組帶有閾值的仿真退化軌跡

圖4 9組截斷退化過程

3.2 結果和討論

首先，將3.1節中的20組仿真數據代入傳統的基于相似性的方法和本文模型中，運行設備的RL估計值如圖5所示。從圖5可以明顯看出，本文模型和基于傳統相似性方法均能顯示出運行設備的RL趨勢，但本文模型更加精確。在退化過程的初期，運行設備的退化數據較少，兩種方法的RL估計值均偏離了實際RL，但本文方法的偏離程度相對較小;隨著退化數據的不斷獲取，兩種方法的偏離程度逐漸減小，當實際的RL很小時(t=40 h后)，兩種方法的PRL非常接近。因為當運行設備將要失效時，能夠獲得足夠多的運行設備的退化數據，能夠準確計算運行設備與參考設備間的相似性，因而對于兩種方法，運行設備的RL估計值PRL(k)與實際RL相差不大。

圖5 運行設備的PRL

圖6 RL估計值的估計誤差

為了定量比較運行設備的RL估計精度，這里引入RL估計值的估計誤差(AE)評價RL估計的精度，估計誤差可以表示為

其中，PRL0(k)表示運行設備在第k個狀態監測點的RL估計值，ARL0(k)表示設備在第k個狀態監測點的實際RL。RL估計值的估計誤差如圖6所示。可以看出，在運行設備的壽命周期內，本文模型的RL估計誤差均小于基于傳統相似性方法的RL估計誤差，且本文模型的RL估計誤差波動較小，因而本文模型優于傳統的基于相似性的方法。

根據上述研究，非負整數與RL估計有著密切關系。本文選擇非負整數H=2，5，8，10，13，18，并且利用3.1節中的20組仿真數據研究H的影響。為量化H的影響，RL估計效果G可定義為

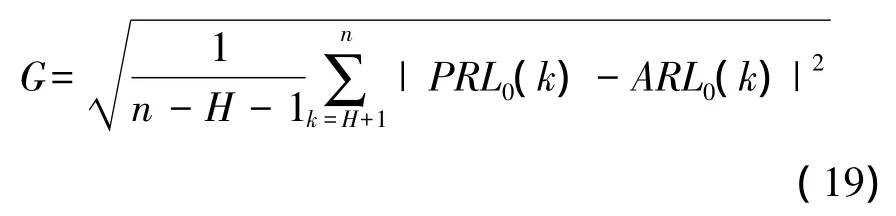
其中，n為運行設備的全部狀態監測點，ARL0(k)表示設備在第k個狀態監測點的實際RL。

根據式(19)，能夠得到RL估計效果，結果如圖7所示。

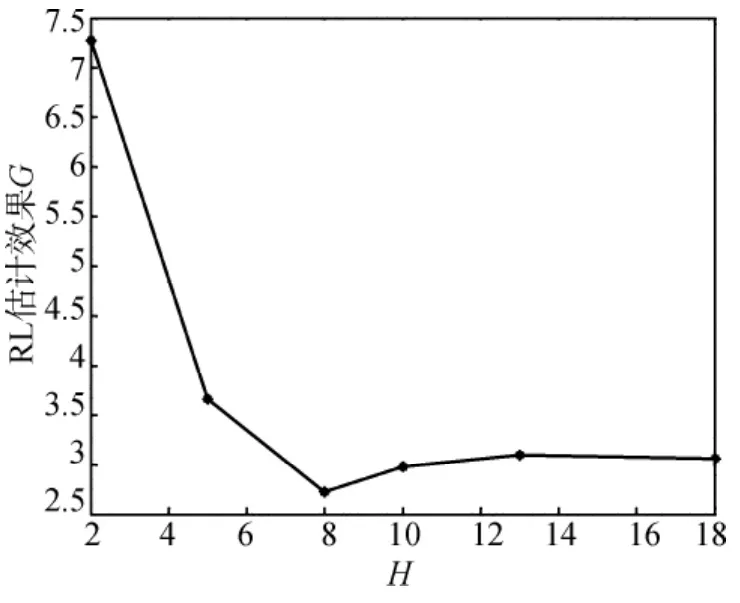
圖7 不同非負整數H下的RL估計效果

從圖中能夠直觀看出，H的取值與RL估計效果有著密切關系。當H值很小時(如H=2)，RL估計效果G的值很大，即本文方法效果較差。在一定范圍內，隨著H的增加，RL的估計效果將明顯提高。因此，當缺乏先驗知識時，H值應該較大一點，但當H值超過一定范圍內，RL的估計效果將會降低，因為H值選擇太大時，本文方法的復雜性將大大增加。故根據圖7可得H=8時RL估計效果最佳。

4 結束語

本文針對非線性隨機退化設備，在相似性的框架下，提出一種基于非線性擴散過程的RL估計方法。首先基于擴散過程構建隨機退化模型，利用截斷設備的退化數據實現其RL的估計;然后基于相似性原理確定參考設備相對于運行設備的權重，最后實現運行設備的RL估計。數值仿真驗證了本文方法優于傳統的基于相似性的方法。研究結果表明，本文綜合利用失效設備和截斷設備的退化數據，提高運行設備的RL估計精度，因而在工程實際中，更具有潛在應用價值。

［1］PECHT M G.Prognostics and Health Management of Electronics［M］.John Wiley:New Jersey，2008:201－211.

［2］司小勝，胡昌華，周東華.帶測量誤差的非線性退化過程建模與剩余壽命估計［J］.自動化學報，2013，39 (5):590－601.

［3］李明福，胡昌華，周志杰，等.基于退化數據的貯存設備最優檢測策略［J］.系統工程與電子技術，2015，37 (5):1219－1223.

［4］SI X S，WANG W B，HU C H，et al.Remaining useful life estimation—A review on the statistical data driven approaches［J］.European Journal of Operational Research，2011，213(1):1－14.

［5］WANG Z Q，HU C H，WANG W B，et al.A simulationbased remaining useful life prediction method considering the influence of maintenance activities［C］//Proc.of the Prognostics and System Health Management(PHM) Conference，2014:284－289.

［6］SHEN Y，TANG L C，XIE M.A model for upside－down bathtub－shaped mean residual life and its properties［J］.IEEE Transactions on Reliability，2009，58(2):425－431.

［7］SI X S，WANG W B，HU C H，et al.Remaining useful life estimation based on a nonlinear diffusion degradation process［J］.IEEE Transactions on Reliability，2012，61 (1):50－67.

［8］WANG W B，CARR M，XU W J，et al.A model for residual life prediction based on Brownian motion with an adaptive drift［J］.Microelectronics Reliability，2011，51(1):285－293.

［9］WANG T，YU J，SIEGEL D，et al.A similarity－based prognostics approach for remaining useful life estimation of engineered systems［C］//Proceedings of International Conference on Prognostics Health Manage，Denver，2008.

［10］ZIO E，MAIO F D.A data－driven approach for predicting the remaining useful life in dynamic failure scenarios of a nuclear system［J］.Reliability Engineering and System Safety，2010，95(1):49－57.

［11］YOU M Y，MENG G.A generalized similarity measure for similarity－based residual life prediction［J］.Proceedings of the Institution of Mechanical Engineers，Part E:Journal of Process Mechanical Engineering，2011，225(3):151－160.

［12］YOU M Y，MENG G.Toward effective utilization of similarity based residual life prediction methods:Weight allocation，prediction robustness，and prediction uncertainty［J］.Proceedings of the Institution of Mechanical Engineers，Part E:Journal of Process Mechanical Engineering，2013，227(1):74－84.

［13］YOU M Y，MENG G.A framework of similarity－based residual life prediction approaches using degradation histories with failure，preventive maintenance，and suspension events［J］.IEEE Transactions on Reliability，2013，62(1):127－135.

［14］WANG Z Q，HU C H，WANG W B，et al.An Additive Wiener Process－Based Prognostic Model for Hybrid Deteriorating Systems［J］.IEEE Transactions on Reliability，2014，63(1):208－222.

［15］LEE M L T，WHITMORE G A.Threshold regression for survival analysis:Modeling event times by a stochastic process reaching a boundary［J］.Statistical Science，2006，21(4):501－513.

(編輯:李妮)

A model for residual life estimation based on the nonlinear diffusion process under the framework of similarity

PEI Hong，HU Changhua，WANG Zhaoqiang，ZHANG Zhengxin，ZHANG Huihui
(302 Unit，Rocket Force University of Engineering，Xi’an 710025，China)

Residual life(RL)estimation is a key part in prognostics and health management(PHM).In current literature，traditional similarity－based RL estimation model can only utilize the degradation data of failed devices，while ignoring the degradation data of suspended devices and operating device，which cannot guarantee the accuracy of the RL estimation.Aiming at this issue，this paper develops a new diffusion process driven RL estimation model in the framework of similarity.Firstly，the degradation model is constructed and the RL of the suspended devices is estimated.And then the observed degradation data from the reference devices(i.e.failed and suspended devices)and the operating device are utilized to estimate the RL of the operating device by comparing the similarity between the operating device and reference devices.Finally，a numerical simulation is provided to substantiate the superiority of the proposed model over the traditional similarity－based approach.The research result shows that the proposed model can remarkably improve the accuracy of the RL estimation for the operating device，which can be potentially applied in practice.

residual life;diffusion process;similarity;reference devices

A

1674－5124(2016)11－0006－07

10.11857/j.issn.1674－5124.2016.11.002

2016－04－13;

2016－06－20

國家杰出青年基金(61025014);國家自然科學基金(61174030，61374120，61573365)

裴洪(1992－)，男，安徽霍邱縣人，碩士研究生，專業方向為預測與健康管理。