天線柱面近場測量的散射源誤差抑制方法研究
王義,陳運濤,溫中賀,劉浩
(1.武漢軍械士官學校,湖北武漢430075;2.中國人民解放軍66029部隊,內蒙古蘇尼特古旗011299; 3.中國電子科技集團公司第38研究所,安徽合肥230031)
天線柱面近場測量的散射源誤差抑制方法研究
王義1,陳運濤1,溫中賀2,劉浩3
(1.武漢軍械士官學校,湖北武漢430075;2.中國人民解放軍66029部隊,內蒙古蘇尼特古旗011299; 3.中國電子科技集團公司第38研究所,安徽合肥230031)
根據柱面波近遠場變換基本原理,引出柱面波模系數與輻射源空間位置的特定約束關系,提出一種先將柱面波譜數據進行濾波處理,然后進行波譜遠場變換,最終得到抑制散射誤差后的遠場方向圖的方法。隨后通過構建陣列天線模型,對抑制效果進行仿真分析。結果表明:該方法在第Ⅰ副瓣位置可改善2dB,120°范圍內方向圖與理想結果較為吻合,能有效抑制散射誤差對遠場方向圖產生的影響。
柱面近場測量;柱面波;遠場方向圖;散射;模式濾波
0 引言
近年來,隨著新體制雷達、微波通信、探測制導等領域的不斷發展,對各種高性能天線設計的要求也不斷提高,作為天線設計和驗證的重要手段,以平面、柱面、球面測量技術為代表的天線近場測量技術[1]因其快速、準確、全天候、高保密性的工作特點得到廣泛應用。其中柱面天線近場測量技術在方位面通過被測天線旋轉,避免平面測量技術因水平截斷帶來的截斷誤差,最大限度地保持水平面遠區輻射特性,特別適用于水平面為寬波束天線的測量[2]。
由于近場測量技術確定天線特性是一種間接的測量方法,由各種因素帶來的誤差很多,大致可以分為4個部分,即探頭誤差、測量系統誤差、環境誤差及隨機誤差。針對各種誤差的分析和補償,國內外許多學者做了相關研究工作,文獻[3]對柱面近場中的各種誤差源進行了分析和歸類,并通過仿真的方法對誤差影響做出分析;文獻[4-7]針對探頭誤差做了評估和相應補償處理;文獻[8]針對隨機噪聲的影響做了定性和定量分析;文獻[9]對超低副瓣天線在平面近場測量條件下的各種誤差和補償方法做了理論研究,這對于柱面近場條件下的誤差補償具有指導意義。然而由于實際測量環境的限制無法實現對電磁波的完全吸收,而較大的電磁波散射和反射勢必會對最終測量結果產生影響,進而在通過近遠場變換遠場特性時產生較大誤差,而相關文獻沒有對這種誤差進行相關研究。
為了解決上述問題,減小多次反射或散射對測試結果的影響,本文從柱面近遠場變換原理出發,通過構建柱面波譜與被測天線的限制關系,基于此約束關系對測量結果進行濾波處理,最后通過構建近場測量模型進行仿真分析,驗證該方法的處理效果。
1 基于柱面波譜的近遠場變換
柱面近場天線測量[1]是在小于最小遠場距離的近場區域內,通過驅動方位轉臺和垂直掃描架的運動,使得探頭天線在包圍被測天線的柱面柵格點上進行采樣,得到被測天線在柱面區域內的輻射能量分布,最后通過近遠場變換,最終得到天線遠場特性的一種近場測量方法。
在線性、各項同性的自由空間中,被測天線為發射狀態下,包圍被測天線的電磁場可以表示為一組正交的圓柱模的疊加,通常用積分式來表示。

相反的,可以通過對包圍天線的柱面上的電磁場分布進行反變換得到正交圓柱模及系數,通常可以利用快速傅立葉變換(FFT)來實現。
當觀察點位于近場區域內(通常取3λ≤ρ≤10λ),假設在包圍被測天線的圓柱表面上用理想極小偶極子探頭得到一組正交的電場分布Ez和E?,因此兩組正交的柱面模系數可以由下式得到,

在這里,自由空間波矢量在z方向上的分量γ和柱面波指數n由負無窮大到正無窮大,?和z表示方位和垂直方向上的坐標,ρ為柱面半徑,如圖1所示,k0是自由空間的傳播常數,H(1)nz ()為一類漢克爾函數,H'(1)n(z)為一類漢克爾函數的導數。

圖1 柱面坐標示意圖

由被測天線近場某一柱面上的場分布,通過數學變換公式變換后,就可以得到被測天線在遠場的輻射特性。
2 基于模式濾波的散射抑制方法
根據柱面近遠場變換條件,假設除被測天線所占空間之外,皆為線性、無源、各項同性的自由空間。從式(1)可以推出,在包圍有源場的任意柱面均產生相同的場分布結果,表明其具有相同的柱面波模系數。
考慮到當κ>k0或γ>k0時,γ或κ為純虛數,,因此必須滿足,并且,因此在柱面波模系數與有效輻射源所在實際空間存在著固定的約束關系。如果除了被測天線作為發射源外,在此圓柱區域內還存在各種散射源的影響,如探頭與被測天線間反射,掃描架散射、地面及吸波材料反射影響等,由于此散射源也包括在柱面區域內,會對遠場結果造成影響,在遠場中無法進行分離,但可以在柱面波譜域范圍內,根據被測天線的實際空間關系進行處理。
假設一轉臺中心為坐標中心,包圍被測天線的最小圓柱半徑為rt0,由柱面波展開式可知如無散射源,柱面波系數與圓柱半徑的選取無關,因此當柱面波指數和z向波矢量分量滿足n2+(γrt0)2>(k0rt0)2時,柱面波函數應為散射源產生,需在得到柱面波系數后將其濾除。
具體處理流程如圖2所示。
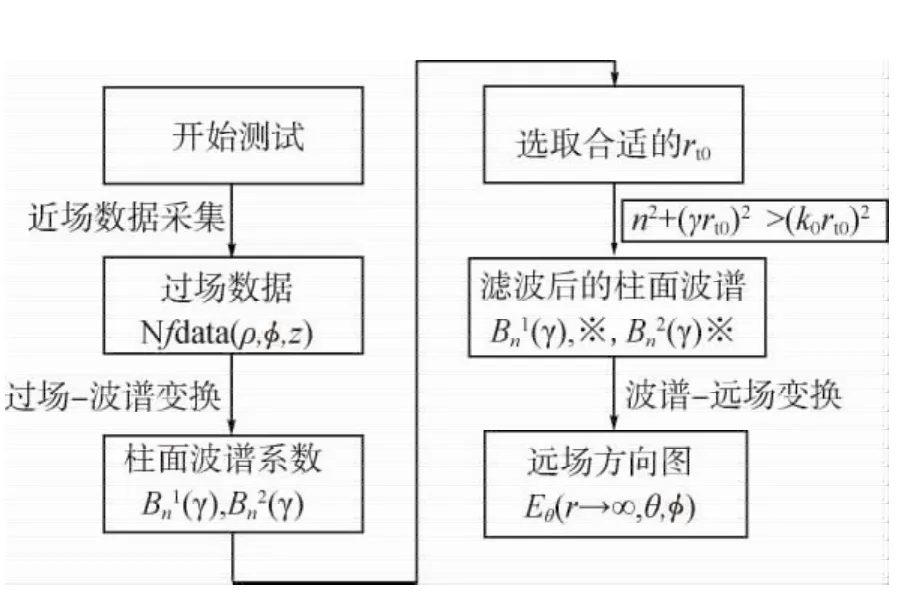
圖2 濾波處理流程圖
3 算法驗證及結果分析
為驗證柱面近場測量原理及散射濾除方法,構建一個半波陣子陣列天線,如圖3所示。

圖3 半波陣子陣列天線示意圖
陣列天線工作頻率為9 GHz,其中陣子沿z軸放置,單元間距0.5λ,x軸放置10個天線單元,z軸放置8個天線單元,z軸掃描范圍為1300 m,掃描間隔16 mm,方位角掃描范圍0°~360°,掃描間隔1.2°,每個陣子單元饋電幅相一致均勻饋電。
陣中第(i,l)個單元在觀察點(x,y,z)處產生的電場z向分量為

其中Im為饋電幅相因子,R1為陣子上端點到場點的距離,R2為陣子下端點到場點的距離,k0為自由空間波數因子。由于陣子為理想偶極子,E?分量可忽略。最終得到柱面的電場z向分量Ez的近場幅相分布如圖4所示。

圖4 無散射柱面近場幅度分布
假設在柱面范圍內加入一個固定散射源,同樣用陣子模擬,得到的近場幅相分布如圖5所示。

圖5 有散射柱面近場幅度分布
根據柱面波系數表達式,利用FFT得到加入散射源前后的柱面波系數分布如圖6、圖7所示。

圖6 無散射柱面波系數幅度分布

圖7 有散射柱面波系數幅度分布
從上圖可以明顯看出散射源在(γ,n)被測天線產生的柱面波系數上及周圍產生變化。由陣列模型可知,包圍陣列天線的最小圓柱半徑為75 mm,考慮到實際天線輻射源會超出這一范圍,取108 mm,以此為半徑ρ得到的濾除散射后的柱面波系數如圖8所示。

圖8 有散射濾波后的柱面波系數幅度分布
將處理前后的柱面波系數通過柱面波遠場表達式得到兩組遠場方向圖,并與理論結果進行對比,如圖9、圖10所示。

圖9 方位向幅度方向圖結果對比

圖10 俯仰向幅度方向圖結果對比
從以上仿真結果可以看出,處理前的方位和俯仰方向上的方向圖與理論結果想比較,第1副瓣相差約2 dB,而處理后的方向圖在方位角30°~150°范圍內均與理論結果較為吻合。從柱面波系數譜分布可以看出,通過濾波處理,雖然濾除了被測天線柱面波系數譜區域外的柱面波,但無法濾除該區域內的影響,從而在30°~150°之外的遠場方向圖產生較大誤差。
4 結束語
針對柱面近場天線測量過程中散射對天線測量結果造成的誤差,介紹了一種基于模式濾波技術的柱面近遠場變換方法。被測天線的柱面近場分布可以分解為柱面波模函數與模系數疊加形式,并且柱面波近遠場變換中柱面波系數與被測天線的尺寸存在約束關系。本文根據這種關系提出先對柱面波譜進行濾波處理而后再進行波譜-遠場變換得到遠場方向圖的方法,隨后通過構建陣列天線模型,對散射誤差的抑制效果進行仿真分析。結果表明該方法能對較大散射環境中的測量數據進行處理,處理后的方向圖在一定范圍內得到較大改善。
[1]YAGHJIAN A D.Near-Field Antenna Measurements On a Cylindrical Surface:A Source Scattering MatrixFormulation[J].NBS Technical Note 696,1977.
[2]ARTHUR D,YAGH J.An overview of near-field antenna measurement systems[J].IEEE Antennas Propag Mag 1986,34(6):754-768.
[3]CASTANER M S,MARTINEZ S B,JIMENEZ F M,et al.Error Analysis and Simulator in Cylindrical Near Field Antenna Measurement Systems[C]//The Second European Conference on Antenna and Propagation,EuCAP 2007(6):1649-1653.
[4]ALLEN C N.Upper bound-error in far field antenna paprameters determined from near field measurement,part 2: analysis and computer simulation[C]//Lecture Notes,National Bureau of Standars Bouler,Coll.Huly,1975:170-201.
[5]LEACH W M,PARIS D T.Probe Compensated Near-Field Measurements On A Cylinder[J].IEEE Trans.on Antennas and Propagation,1973141:435-444.
[6]HUSSEIN Z A.Probe Compensation And Error Analysis In Cylindrical Near-Field Scanning 16th annual Antenna and Measurement Techniques Symp[M].AMTA,Symposium,Digest,Long Beach California:1994.
[7]BORGIOTTI G V.Integral Equation Formulation for Probe Corrected Far-Field Reconstruction from Measurements on a Cylinder[J].IEEE Transactions on Antennas and Propagation,1978(4):572-578.
[8]ROMEU J,JOFRE L,CARDAMA A.Far-field errors due to random noise in cylindrical near-field measurements[J].IEEE Transactions on Antennas and Propagations,1992,40(1):79-84.
[9]張福順.超低副瓣天線平面近場測量誤差分析與補償技術研究[D].西安:西安電子科技大學,1999.
(編輯:劉楊)
Research on scattering source error suppression method for antenna cylindrical near-field measurements
WANG Yi1,CHEN Yuntao1,WEN Zhonghe2,LIU Hao3
(1.Wuhan Institute of Ordnance Officer,Wuhan 430075,China;2.PLA Unit 66029,Sonid Right Banner 011299,China; 3.China Electronics Technology group Corporation No.38 Research Institute,Hefei 230031,China)
According to the cylindrical wave near field to far field transformation principle,a constraint relationship between mode coefficient of cylindrical wave and position of radiation source space is presented,Then a new method is proposed to filter the cylinder spectrum data,and then carry out the spectral far field transformation.Finally,the far field pattern of the scattered error is finally obtained.Then,the suppression effect is simulated and analyzed by building the model of the array antenna.It shows that an improvement of 2dB in the first sidelobe positions by suppression method.Within the range of 120°,the post results and the ideal results are in good agreement,the method effectively inhibited the scattering effect on the far field pattern.
cylindrical near-field measurements;cylindrical wave;far field pattern;scattering;mode filtering
A
1674-5124(2016)11-0023-04
10.11857/j.issn.1674-5124.2016.11.005
2016-04-10;收修改稿日期:2016-06-11
王義(1979-),男,吉林雙遼市人,副教授,碩士,研究方向為電磁兼容、復雜電磁環境下的電子對抗。

