對孿生素數沒有窮盡問題的證明

張爾光

【摘 要】本文根據素數2、3、5的有效排除作用，創建了自然數“235狀態”和“6×m±1”等式，并通過自然數“235狀態”這個“窗口”對新生素數、孿生素數、四子孿生素數的特征進行了解讀，對孿生素數以及四子孿生素數沒有窮盡問題做出證明。

【關鍵詞】自然數“235狀態”；孿生素數；四子孿生素數；破壞力；沒有窮盡

筆者研究結果表明，孿生素素是沒有窮盡的，四子孿生素數也是沒有窮盡的，并始終與自然數沒有窮盡的過程同存相隨。那么，對于孿生素數沒有窮盡問題的證明，可通過素數有效排除力、“235狀態”自然數、孿生素數對數三者關系找到其證明思路。

1 自然數“235狀態”

定義1：自然數原始狀態。是指自然數按“1、2、3、4、5、6、7、8、9、10……”次序排列，沒作任何改動的原本情形。

定義2：自然數“235狀態”。是指自然數原始狀態在經將可被素數2、3、5整除的自然數排除出去（即篩選）之后形成的情形（見表1）。

…

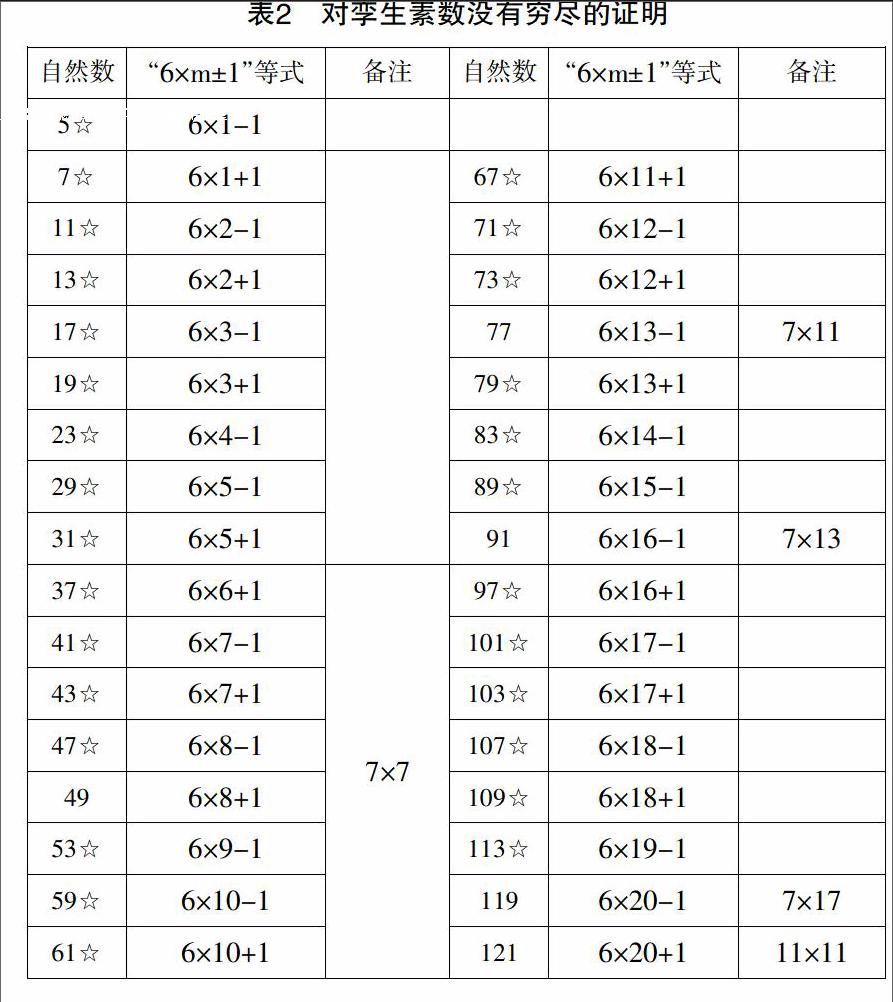
定義3：孿生素數。是新生素數的組成部分。是指“6×m±1”等式中同一個等式的兩個得數，且此兩個得數同是非合數的自然數。如素數5與7是同為“6×1±1”等式的兩個非合數的得數，又如素數29與31是同為“6×5±1”等式的兩個非合數的得數。

定義4：四子孿生素數。是指其他位數數字相同、只是個位數數字不同并依次為“1、3、7、9”，同時又是非合數的4個自然數。四子孿生素數也是相連的兩個“6×m±1”等式的同為非合數的4個得數。如素數11、13、17、19是“6×2±1”和“6×3±1”兩個相連等式的4個同為非合數的得數。四子孿生素數又稱為“連組孿生素數”。

在素數中，2是首位素數，3是首位奇素數，5是首位新生素數。從素數的有效排除力來說，2、3、5是排在前3位的素數，此3個素數的有效排除力之和為22/30，超過素數的有效排除力總和的2/3。從表1看出，自然數原始狀態在經將可被素數2、3、5整除的自然數排除出去（即篩選）之后，以30個自然數為1個擴圍單位，30個自然數中有22個被排除（即篩選）。盡管如此，所剩留下的自然數的個位數為“1、3、7、9、3、9、1、7”這樣一種格局有序排列，形成的情形是新生素數整體格局的雛形。